复杂电磁力作用下10 kV交流电机端部绕组绝缘损伤应力强度分析

张海军， 张明杰， 陈小勇， 万少华， 郭 季

（1.湖北文理学院 纯电动汽车动力系统设计与测试湖北省重点实验室，湖北 襄阳 441053；2.新昇电气有限公司，湖北 襄阳 441899）

0 引 言

牵引电机作为交流电力机车的核心设备之一，其健康状态关系到整个列车的安全与稳定运行。一旦发生事故，除了电机本体检修周期比较长，还可能造成巨大经济损失，甚至带来严重的社会影响。统计表明，端部绕组故障是直接或间接导致牵引电机事故的主要原因之一[1-2]。随着机车牵引速度与功率的增大，受复杂、恶劣工作环境因素（高温、负载波动大、高频振动）影响，牵引电机绕组将长期工作在以强电磁力为主要力，辅以机械应力和热应力等综合力的作用下，导致电机端部绕组故障概率显著提高[3-4]。端部绕组绝缘层破坏是典型的电机故障之一，如图1所示。

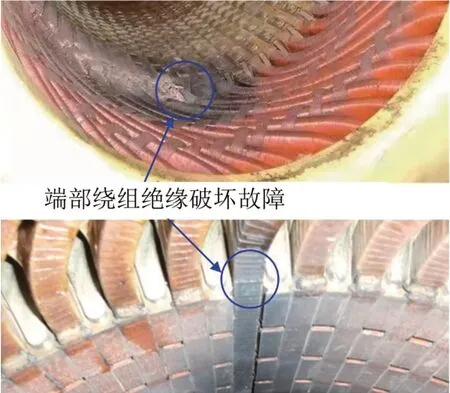
图1 电机端部绕组故障Fig.1 Fault of motor end winding

目前关于端部绕组的研究主要集中在绕组电磁力计算、电磁力引起的动态变形以及振动分析方面，文献[5]基于有限元法分析了发电机定子端部绕组电磁力及端部绕组单匝的应力和应变分布。文献[6]采用有限元体积法研究了在额定载荷条件下定子端部绕组表面的传热系数分布、流体流动分布和端部绕组的温度分布。文献[7]提出了一种同时考虑端部绕组边缘效应和漏磁通的新方法，可用于计算端部绕组的漏电感。文献[8]采用有限元法研究了过渡状态和稳态的电磁场，用数值方法研究了电机端部绕组电磁力引起的振动。文献[9]通过三维有限元法得出了电机稳态运行时整个端部绕组的电磁力和应力分布，并和铜的屈服强度进行了比较。

近年来，国内外学者通过在电机端部绕组电磁力计算宏观受力及其振动规律方面的深入研究，获得了足够精度的端部绕组电磁力分布，然而绕组受电磁力作用引起导体变形以及绝缘层破坏的机理还有待进一步研究。统计表明[10-11]，端部绕组早期故障形式主要表现在绝缘层的破坏，例如出现不同程度的裂纹损伤。随着牵引电机频繁启动和加减速的工况变化，端部绕组绝缘层裂纹在综合应力作用下将出现不同程度的扩展，导致绝缘加剧破坏，严重时甚至会引起绝缘击穿和短路故障。

本研究以某型号大功率牵引电机为例，建立其端部绕组的三维有限元模型，并利用有限元方法计算裂纹在电磁力作用下的应力应变状态。基于断裂力学理论，探究端部绕组绝缘层裂纹扩展和破坏机理，并通过应力强度因子对裂纹扩展程度进行评估。

1 绕组绝缘损伤断裂理论

1.1 电磁与机械应力应变分析

电机端部绕组的电磁力分布复杂且具有交变特性，会引起绝缘层内部不规则的应力应变状态变化。因此，确定绕组导体和外层绝缘的内应力应变状态是进行端部绕组绝缘损伤断裂机理研究的前提[12]。

根据洛伦兹力定律，电磁力可表示为式（1）。

式（1）中：F为电磁力；J为电流密度；B为磁通密度。

根据弹性形变分析理论，应力应变控制方程如式（2）所示[13]。

式（2）中：σz为z方向应力分量；σr为r方向应力分量；σθ为θ方向应力分量；τrz为剪切应力分量。

表征绕组铜导体材料内部应力应变状态关系的几何方程组如式（3）所示。

式（3）中：εz为z方向应变分量；εr为r方向应变分量；εθ为θ方向应变分量；γrz为剪切应变分量；uz为z方向位移；ur为r方向位移。

一般应力状态下的各向同性材料本构方程组如式（4）所示。

式（4）中：E为弹性模量；υ为泊松比。

1.2 绝缘层损伤断裂的应力强度因子

电机端部绕组不可避免地会受到加工、装配过程中的机械碰撞以及质量缺陷的影响而产生初始损伤，主要表现为埋藏裂纹和表面裂纹。此外，受材料老化因素影响，绕组长期工作在复杂电磁-机械应力综合作用下，绝缘层裂纹将进一步扩展演化[14]。在电机绝缘中天然材料云母占主要地位，为了量化评估和表征绕组绝缘层受应力作用后引起的裂纹断裂和扩展程度，本研究以云母材料的表面裂纹为例[15]，引入应力强度因子对裂纹断裂程度进行量化描述，如式（5）所示。

式（5）中：KI、KII、KIII分别对应张开型、滑开型、撕开型裂纹尖端的应力强度因子；U、V、W分别为局部笛卡尔坐标系下的位移分量；r为局部圆柱坐标，如图2所示；G为剪切量；k如式（6）所示。

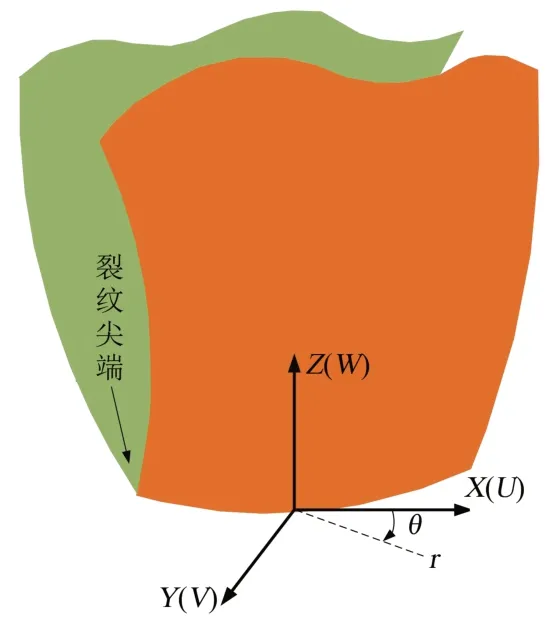
图2 三维裂纹尖端局部坐标Fig.2 Local coordinates of three-dimensional crack tip

在断裂理论力学中，应力强度因子是表征裂纹尖端应力应变场的重要参数，其值越大，裂纹越容易扩展。用应力强度因子表征裂纹尖端节点位移，如式（7）所示。

2 电机端部绕组三维有限元建模

2.1 电机及端部绕组参数

本研究以一台三相交流牵引电机为例进行端部绕组绝缘损伤断裂及破坏强度分析，三维模型如图3所示，模型主要参数如表1所示。

表1 电机及端部绕组参数Tab.1 Parameters of motor and end winding

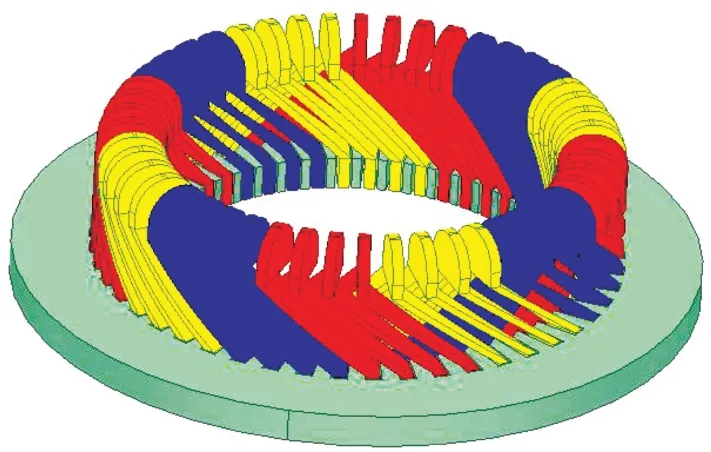
图3 电机端部绕组三维有限元模型Fig.3 Three-dimensional finite element model of motor end winding

2.2 端部线圈建模与裂纹初始状态模拟

在牵引电机实际运行中，其端部绕组长期处于不均衡、交变的电磁力作用下，端部绕组受力非常复杂且呈现不对称性，特别是绑扎的端部绕组线圈容易受振动影响出现松动，应力应变状态较为复杂[16]。本研究重点针对端部绕组松动后，线圈绝缘层损伤断裂的规律进行分析，忽略线圈之间的接触约束影响，同时为了减少有限单元数和计算量，使用端部绕组单根绕组线圈的简化模型，如图4所示。为了提高计算精度，并考虑端部线圈结构和受力的不对称性，采用三维有限元法对其进行数值分析。

为了更准确地分析端部绕组在电磁力作用下的绝缘层损伤演化，本研究中线圈模型考虑了实际绕组的构成。图4中线圈模型包括铜导体和外部绝缘层，黄色部分为端部绕组内部的线圈导体，红色部分为线圈绝缘。建模中，将端部线圈外层绝缘设置为一个整体，而将导体分为16段，其中线棒部分各分为7段，线圈鼻端分为2段，以便更真实、精确地对导体加载电磁力。加载后的电磁力如图5所示。

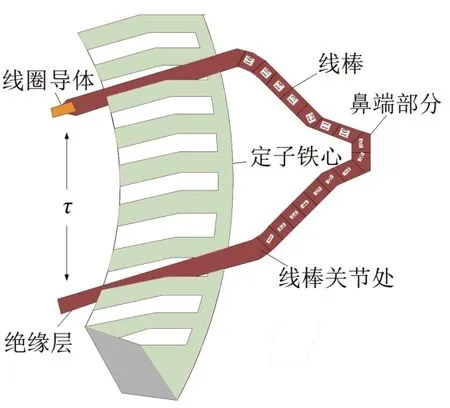
图4 端部绕组单线圈结构Fig.4 End winding single coil structure

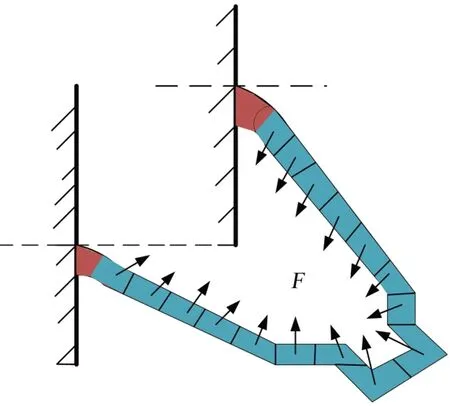
图5 端部绕组受力结构图Fig.5 Force structure diagram of end winding

2.3 绝缘层初始裂纹状态模拟

电机端部绕组短路早期故障主要表现为绝缘层裂纹损伤，本研究对绝缘层进行初始裂纹建模。通过在绝缘层表面设置半椭圆裂纹来描述绕组绝缘的初始损伤状态，如图6所示。图6中l表示初始裂纹的主半径，b表示初始裂纹的最大轮廓半径，h表示初始裂纹的次半径。考虑到裂纹与绝缘层有限单元结构的影响，绕组导体、绝缘层分别采用六面体和四面体单元进行剖分，网格剖分单元尺寸为10 mm，总单元数为34 853，总节点数为105 125。图7为初始裂纹尖端网格划分放大情况。

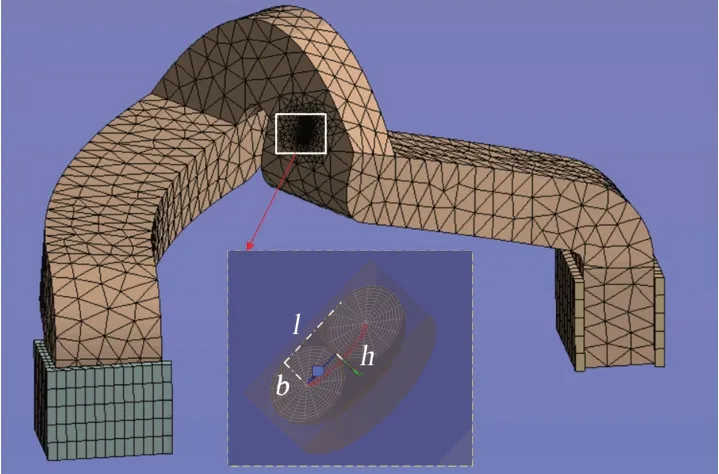
图6 端部绕组初始裂纹建模Fig.6 Initial crack modeling of end winding

图7 初始裂纹尖端网格划分Fig.7 Meshing of initial crack tip

3 算例及结果分析

利用有限元软件对电机端部绕组进行瞬态磁场仿真计算，求解得出绕组云图，其中整体定子端部绕组电磁力密度如图8所示，单根定子端部绕组电磁力密度如图9所示。由图8～9可知，整体电机端部绕组电磁力密度呈现对称且规律性变化，且关节部位电磁力密度大于鼻端部位。

图8 整体定子端部绕组电磁力密度Fig.8 Electromagnetic force density of integral stator end winding

图9 单根定子端部绕组电磁力密度Fig.9 Electromagnetic force density of single stator end winding

3.1 端部线圈集中应力分析

在电机运行中端部绕组会受到较为复杂的电磁力作用，通常裂纹在应力集中位置更容易扩展。分析有限元数值计算结果，发现端部绕组受电磁力作用后应力集中，应变峰值主要出现在铁心槽口附近，如图10所示。图10中，在铁心槽口处的线圈绝缘层上设置不同的采样点进行应力应变状态比较和定量分析。

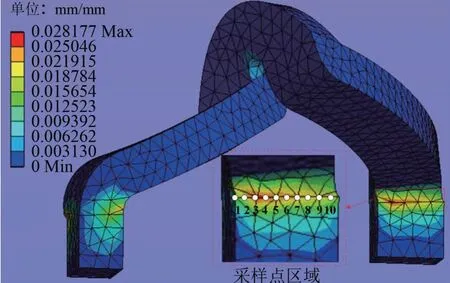
图10 十个采样点的应变分布图Fig.10 Strain distribution map of ten sampling points

图11和图12分别为不同采样点对应的应力应变值，其应力应变值的结果变化与理论上公式（2）、（3）中应力应变的关系相同。从图11～12可以发现，各采样点应力应变状态变化规律基本一致，而采样点3、4、5的应力明显高于其他采样点的应力，且最大应力应变值约为最小应力应变值的2.3倍。

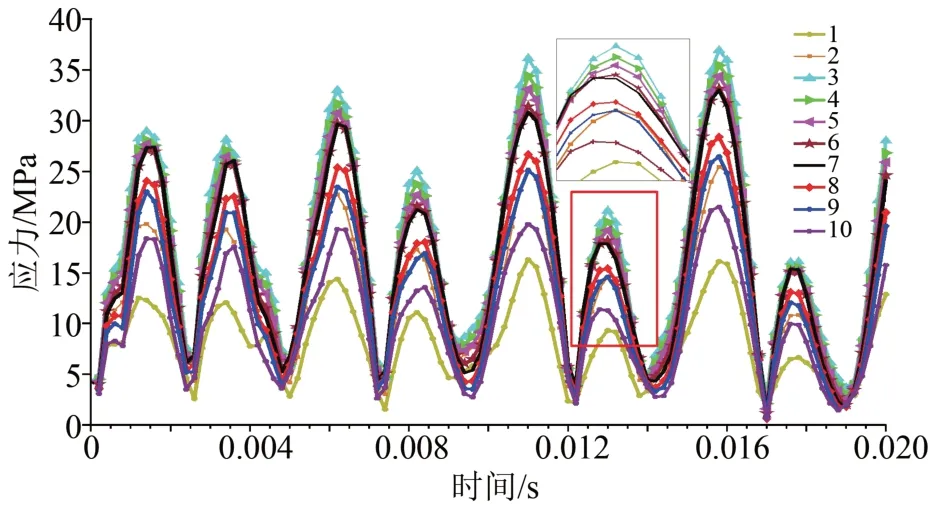
图11 不同点的应力图Fig.11 Stress diagram of different points

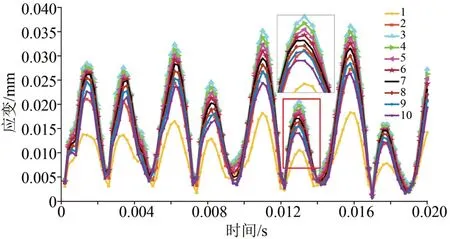
图12 不同点的应变图Fig.12 Strain diagram of different points

图13为绝缘层应力集中位置存在裂纹初始损伤下的应变状态分布。与图10比较可以发现，应变峰值大小和位置都发生变化：应变最大位置转移到绝缘层裂纹的尖端附近，应变最大值显著增大。

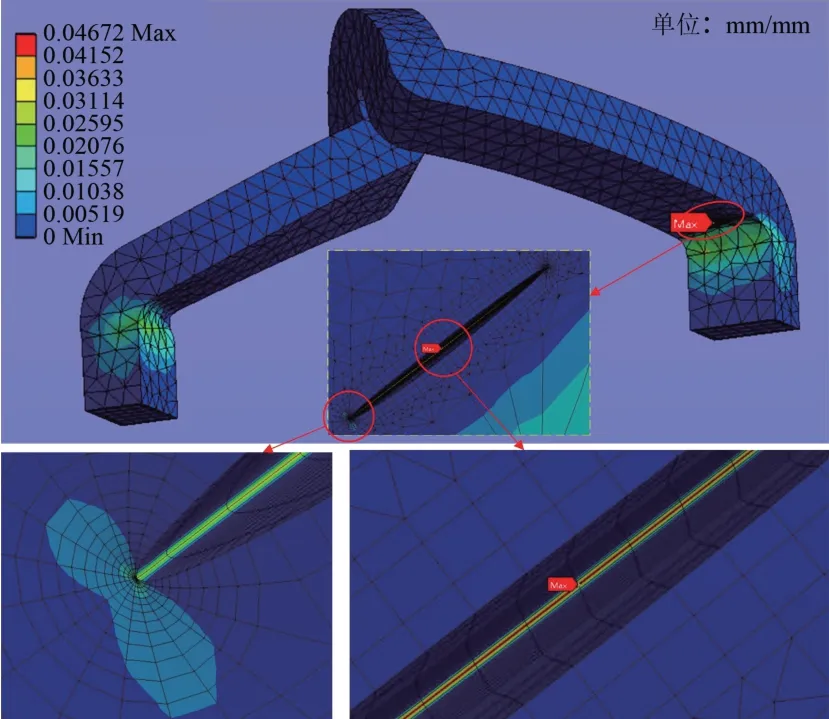
图13 裂纹应变分布Fig.13 Crack strain distribution

3.2 绝缘层裂纹强度分析

为了研究和定量表征裂纹损伤扩展的影响因素，并揭示裂纹断裂损伤扩展规律，分别对不同位置、不同方向以及不同h值的张开型裂纹进行数值计算和结果分析。

3.2.1 不同位置裂纹的强度分析

电机端部绕组线圈的振动变形与悬臂梁结构力学问题类似，一方面铁心槽口位置的应力应变集中比较明显，另一方面绕组鼻端位置的应力应变状态也值得关注[17]。针对上述应力应变比较集中的位置，分别在铁心槽口（端部关节）和鼻端的绕组绝缘层设置相同方向、相同尺寸的裂纹，以分析裂纹位置对裂纹扩展程度的影响，线棒关节处裂纹（裂纹1）和鼻端裂纹（裂纹2）的位移分布计算结果如图14所示。

基于图14中不同位置裂纹尖端（裂纹1和裂纹2）的应变状态值分别计算得到其应力强度因子，如图15所示。由15中曲线数据可知，线棒关节处裂纹的应力强度因子最大值为4.0 MPa·mm2，鼻端处应力强度因子最大值为0.5 MPa·mm2。可以看出，端部关节处应力强度因子是鼻端裂纹应力强度因子的8倍，这表明端部绕组关节处的裂纹损伤扩展程度更大，随着电机启动产生的电磁力频繁冲击，端部绕组关节处裂纹损伤也更容易出现进一步断裂。

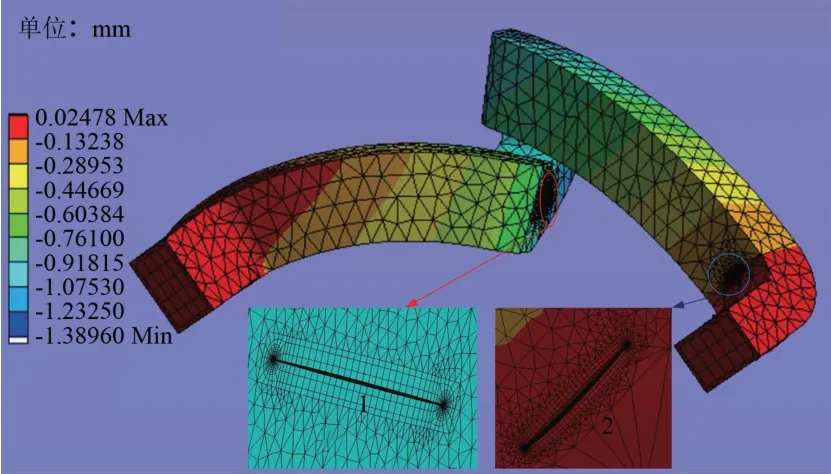
图14 线棒关节处和鼻端裂纹位移分布Fig.14 Deformation distribution of cracks in joint and nose of wire rod

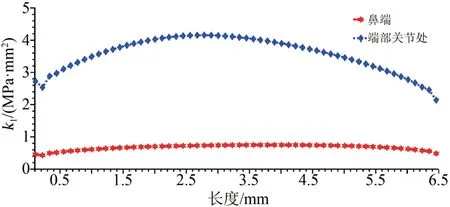
图15 不同位置处的应力强度因子Fig.15 Stress intensity factors at different locations

3.2.2 不同方向裂纹强度分析

实际牵引电机的端部绕组绝缘层初始裂纹裂开方向也具有一定的随机性，图16为不同方向的裂纹分布示意图。为了研究裂纹裂开方向对应力应变状态变化和裂纹扩展程度的影响，本研究针对应力最集中的铁心槽口位置、相同尺寸但不同方向（分别为0°、30°、60°、90°，其中定义0°裂纹为纵向裂纹，90°裂纹为横向裂纹）的绝缘层裂纹分别进行了有限元数值计算。

图16 不同角度的裂纹情况示意图Fig.16 Diagram of cracks at different angles

图17为不同方向的裂纹尖端应力强度因子。从图17可以发现，随着角度从0°逐渐变化到90°，应力强度因子逐渐变大，由60°到90°这一过程中变化幅度最大，且90°对应的横向裂纹应力强度因子最大。这表明90°方向的裂纹更易扩展，使绝缘层损伤程度更大。

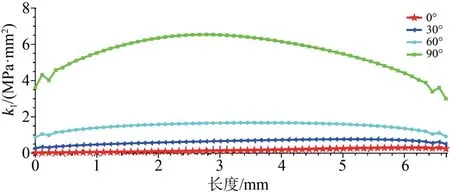
图17 不同角度裂纹的应力强度因子Fig.17 Stress intensity factors of cracks at different angles

3.2.3 不同h值时的裂纹强度分析

为了进一步分析初始裂纹h值对断裂程度及扩展趋势的影响，设定了不同h值的初始裂纹，并设定绕组绝缘总厚度为2 mm，在应力应变集中的同一位置设定大小相同，h值分别为0.4、0.7、1.0、1.3、1.6 mm的裂纹且未设定贯穿裂纹进行计算，分析得出应力强度因子随裂纹h值的变化曲线如图18所示。

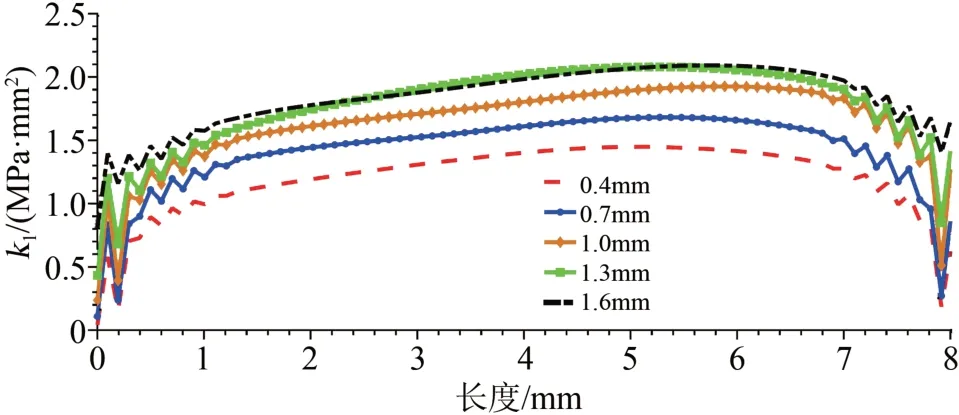
图18 不同h值裂纹的应力强度因子Fig.18 Stress intensity factors of crack with different h value

由图18可以得出，在应力应变最集中的位置处设定大小相同h值不同的裂纹，当裂纹的h值越大时，其应力强度因子越大，在裂纹h值达到一定程度后其应力强度因子可能达到相对最大值（2.0 MPa·mm2），并在一定区域内上下浮动，与公式（5）、（7）中理论结果相对应。表明当初始裂纹的大小相同时，h值越大，绝缘层的损伤程度越大。

4 结 论

本研究分析了电机端部绕组绝缘层的裂纹损伤规律，主要得到以下结论：

（1）端部绕组线棒关节处的裂纹与鼻端位置裂纹的应力强度因子计算结果表明，端部绕组线棒关节处存在的初始裂纹比鼻端位置更容易扩展。

（2）不同方向的裂纹（横向裂纹或纵向裂纹）应力强度因子变化明显，当裂纹呈现为横向裂纹时，裂纹的应力强度因子和裂纹扩展程度更大。

（3）不同h值的初始裂纹应力强度因子也不相同，整体表现为初始裂纹h值越大，应力强度因子也越大，当h值达到一定程度后，其应力强度因子值可能达到最大值。