基于热流固耦合的增强型地热有机朗肯循环发电系统性能分析

王令宝, 郭志鹏 , 卜宪标, 李华山, 龚宇烈*

1)中国科学院广州能源研究所, 广东广州 510640; 2)中国科学技术大学工程科学学院, 安徽合肥 230026

2020年, 我国提出了二氧化碳的碳排放力争于2030年前达到峰值, 努力争取到2060年前实现“碳中和”。2021年, 我国提出了构建新能源占比逐渐提高的新型电力系统, 推动清洁电力资源大范围优化配置(张智刚和康重庆, 2022)。地热能是一种清洁的可再生能源, 具有储量丰富、稳定性强、连续性好、利用系数高等优点(Falcone et al., 2018)。地热能包括水热型和干热岩型, 干热岩一般指赋存于地下3～10 km具有经济开发价值的高温岩体, 我国干热岩资源十分丰富, 调查表明, 我国大陆 3～10 km深度段干热岩资源总量相当于 856万亿吨标煤, 其中埋深5.5 km以内的资源折合106万亿吨标煤(王贵玲等, 2020), 干热岩的开发利用对于“双碳”目标达成和新型电力系统构建具有重要意义(张超等,2022)。

天然状态下的干热岩孔(裂)隙不发育, 裂隙之间连通性较差。增强型地热系统(enhanced or engineered geothermal system, EGS)是目前开发干热岩资源的有效技术手段, 通过水力压裂等工程手段在地下深处的干热岩体中形成载热工质的流动通道,是一种具有广阔发展前景的地热能利用形式。EGS方面的研究主要集中在循环工质优选(Guo et al., 2019; 冯雨晴等, 2021; Liu et al., 2022)、干热岩储层激发(周舟等, 2019; 冯波等, 2019)和采热过程的多物理场耦合数值模拟(孙致学等, 2020; Li et al.,2021; 贺甲元等, 2022)等。研究表明, 循环流体注入条件、循环流体、储层激发效果(裂隙形态、尺寸、分布与连通性)、储层所处的温度场、应力场以及化学作用等多重因素均会影响EGS系统取热性能。

李骥飞(2021)基于不同干热岩开采温度, 进行了发电方式和循环工质的优化及性能分析。Li and Liro(2014)对 200～800 ℃的干热岩地热流体的发电方式进行了分析、考察和对比。Duniam and Guigenci(2016)研究了环境温度对风冷式干热岩有机朗肯循环发电系统的影响规律。Zhang and Jiang(2012)针对 200 ℃以下 4种典型地质流体温度,分析了亚临界、过热和跨临界发电循环的系统性能,比较了R134a、异丁烷、R245fa和异戊烷的系统性能。Meng et al.(2021)针对典型的干热岩资源参数,进行了干热岩驱动的新型超临界CO2循环发电结构改进与热力学优化。这些研究是基于设定的干热岩资源开采温度, 并没有考虑热储参数和布井参数对干热岩发电系统的影响。

Xu et al.(2018)基于两口水平井水循环, 研究了共和盆地恰卜恰地热田裂缝性储层的发电潜力。Zhang et al.(2014)以大庆油田徐家围子地区为例,分析了水平井分段压裂增产油藏采出水循环增强型地热发电系统的性能。Lei et al.(2019, 2020)基于青海共和盆地恰卜恰干热岩资源参数构建了三竖井干热岩发电系统, 研究了注入速率、井距和注入温度对系统性能的影响, 提出了三种干热岩有机朗肯循环发电系统优化方案, 并对其经济和环境效益进行了评估。Zhong et al.(2022)基于青海共和盆地恰卜恰干热岩资源参数, 进行了布井参数和干热岩资源开采参数优化。这些研究针对干热岩热储资源参数建立了热储的流动传热数学模型, 但是并未建立地面发电系统的详细热动力学模型。

通过上述研究可以发现, 有机朗肯循环(ORC)是利用干热岩进行发电的主要技术方式, 耦合井筒、热储和地面发电系统的详细热动力学模型进行数值模拟研究的工作鲜有报道。我国干热岩地热资源勘探和开发起步较晚, 2017年, 中国地质调查局和青海省自然资源厅在青海共和盆地钻获236 ℃高温岩心, 取得了我国干热岩勘查的重大突破(何淼等, 2021)。基于青海省共和县恰卜恰干热岩体地热地质参数(Lei et al., 2020; 唐显春等, 2020, 2023),本文建立了耦合井筒、热储和地面发电系统的全局数学模型, 研究了地热资源开采参数、布井参数对ORC发电系统性能的影响规律。

1 系统描述及数学模型

1.1 系统描述

增强型地热ORC系统的流程图和T-s图如图1所示。为减小地热水对机组的腐蚀结垢风险, 将地热水的热量传递给清水, 然后清水进入 ORC系统的蒸发器, 将低沸点的有机工质加热成过热的有机工质蒸汽, 有机工质蒸汽进入膨胀机, 驱动膨胀机做功, 膨胀机排出的低温低压有机工质乏汽进入冷凝器, 在其中被外部冷却介质冷凝成饱和或者具有一定过冷度的液态工质, 冷凝器出口的液态有机工质经过工质泵的升压后进入蒸发器, 如此循环往复,实现ORC系统的连续运转。Landau and Insheim干热岩电站采用ORMAT公司的有机朗肯循环发电机组, 循环工质均为R601a(Eyerer et al., 2020)。本文的ORC系统也采用R601a作为循环工质, 热物性参数调用NIST的REFPROP 9.1软件(Lemmon et al.,2020)。

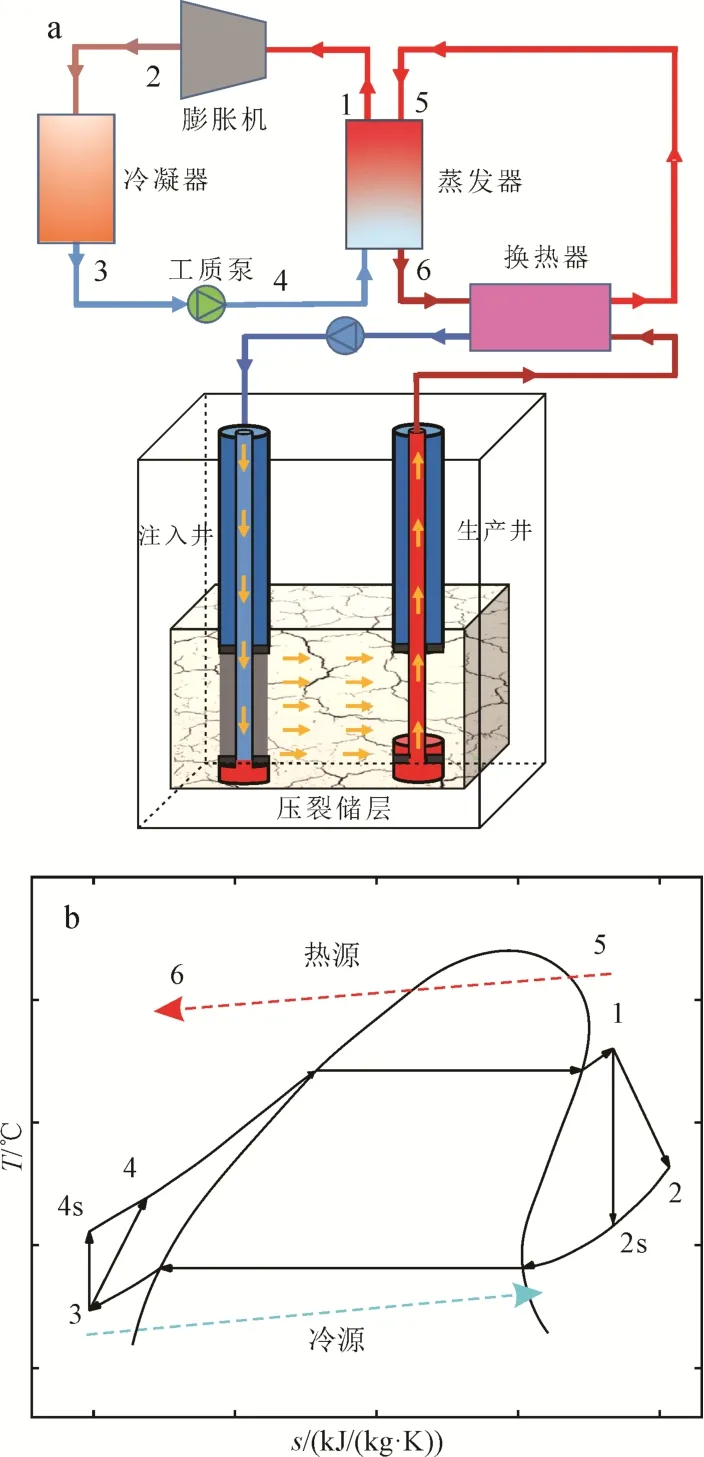
图1 增强型地热ORC系统Fig. 1 Enhanced geothermal system ORC

1.2 模型假设

假设压裂储层为均质、各向同性; 地热水流动服从达西定律; 岩石和地热水的换热满足局部热平衡, 忽略固液两相温差; 岩石在外力作用下发生线弹性变形。岩石基质渗透率与裂缝渗透率相比量级很小, 仅考虑裂隙渗透率与岩石有效应力的关系,忽略岩石基质块渗透率的变化; ORC系统处于稳定流动状态; 忽略ORC系统和环境间的散热损失; 忽略蒸发器、冷凝器和连接管路的压力损失。

1.3 数学模型

1.3.1 热储模型

储层中岩石和裂隙热交换的能量守恒方程为:

式中,T为温度, ℃;uf为水的流速, m/s;ρf为水的密度, kg/m3;Cf为水的比热, J/(kg·K);Qr表示储层中岩石基质和裂缝之间的热量传递, W/m3;df为裂缝孔径, m; (ρC)eff和λeff为有效比热容和有效导热系数, 表示为:

式中,ρm为岩石的密度, kg/m3;Cm为岩石比热,J/(kg·K);λf和λm分别为水和岩石导热系数,W/(m·K);φ为孔隙度。

储层中地热水的流动由达西定律和质量守恒方程表示:

式中,p为孔隙压力, Pa;ηf为水的动力黏度,Pa·s;ρfg▽z表示重力的影响;κm和κf为岩石基质渗透率和裂缝渗透率, m2;e表示由于岩石变形引起的体积应变;Qf为岩石基质和裂缝之间的质量传递,kg/(m3·s);αB为 Biot系数;S为考虑地热水和岩石压缩性的存储系数, Pa-1。

储层岩石变形的力学平衡方程为:

式中,u为位移, m;λ和μ是 Lamé参数, Pa;E为弹性模量;ν为泊松比;Ti为地层的初始温度, K;αT为热膨胀系数;Fi为单位体积力, N/m3;Kd为相同材料多孔基质的排水体积模量, Pa。

岩石变形会改变裂缝的孔径, 从而导致裂缝渗透率发生变化。应力和裂隙渗透率之间的关系可表示为:

式中,κf为裂缝渗透率, m2;κf0为初始渗透率,m2;σ*为标准化常数, 可取值-10 MPa。

1.3.2 井筒模型

井筒换热的能量守恒方程为:

式中,Ac为流道的横截面积, m2;Qwall为通过管壁与外部热交换, W/m;Tm为外部岩石温度, ℃;R为热阻, ℃/W;r1、r2分别为井筒的内、外半径, m;λ为管壁导热系数, W/(m·℃)。

流体和管壁的对流换热系数由下式表示:

式中,Nu为努塞尔数;D为水力直径;Re为雷诺数;Pr为普朗特数;f为达西摩擦系数。

1.3.3 发电系统模型

开采出的地热流体在换热器中将热量传递给清水, 换热器中的能量守恒为:

式中,mgeo和mwater分别为地热流体和清水的质量流量, kg/s;h表示焓值, kJ/kg;cp,water为定压比热容, kJ/(kg·K);T表示温度, ℃; 下标“pro”和“inj”分别表示生产和注入; 下标“5”和“6”对应图1a中的状态点, 下述模型中数字下标均对应图1a中的状态点。

清水与有机工质在蒸发器中以逆流形式进行热交换, 清水放热, 温度不断降低, 有机工质吸热逐步从过冷状态变为过热状态, 蒸发器中清水提供的热量与有机工质吸收的热量相等, 蒸发器中的能量守恒为:

式中,Q为热负荷, 单位kW;mwf为质量流量,单位kg/s; 下标“eva”表示蒸发器。

据共和气象站资料(1980—2012年), 多年平均气温 3.7 ℃, 采用空冷方式, 空气与有机工质在冷凝器中亦是以逆流形式进行热交换, 冷却介质吸热,温度不断升高, 有机工质放热逐步从过热蒸汽变为过冷液体, 冷凝器中冷却介质吸收的热量与循环工质释放的热量相等, 冷凝器中的能量守恒为:

式中, 下标“con”、“in”和“out”分别表示冷凝器、进口和出口。

工质泵对有机工质的增压过程实际上是熵增过程, 工质泵耗功为:

式中,ε表示工质泵的等熵效率; 下标“wp”和“s”分别表示工质泵和等熵过程。

有机工质在膨胀机中膨胀作功也是熵增过程,膨胀机的输出功为:

式中, 下标“exp”表示膨胀机。

地热流体注入泵功耗为:

式中,ρgeo为地热流体的密度, kg/m3;Pinj和Ppro分别为地热流体的注入压力和生产压力, kPa;ε表示工质泵的等熵效率; 下标“injwp”表示注入泵。

增强型地热ORC系统的净输出功为:

增强型地热ORC系统的热效率为:

1.4 模型验证

对于裂隙中流体的流动换热, 可通过图2所示的单裂隙流动换热模型的解析解进行验证(Huang et al., 2020)。该模型假设岩石基质在x和z方向无限延伸, 中间有一条宽度为1 mm的裂隙。初始温度为353.15 K, 注入水流速和温度分别为0.01 m/s和303.15 K。裂隙与岩石的温度通过解析解(Barends,2010)获得。

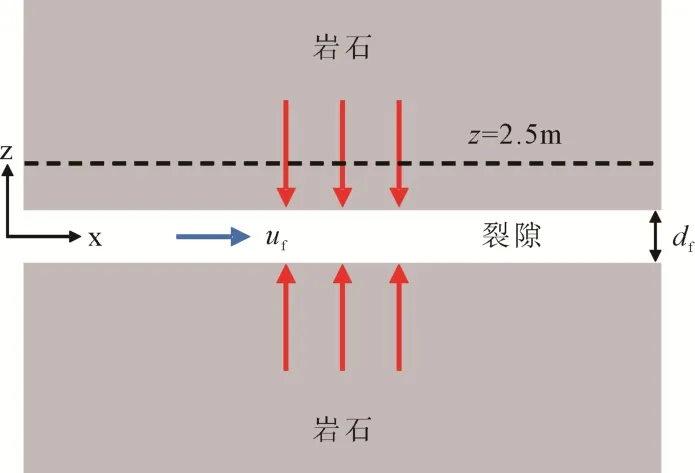
图2 裂隙流动换热物理模型示意图Fig. 2 Schematic diagram of two-dimensional single fracture flow and heat transfer mode

裂隙中的温度分布表示为:

岩石基质中的温度分布表示为:

式中,T为温度, K;λ为导热系数, W/(m·K),c为比热容, J/(kg·K);df为裂缝孔径, m;t为时间, s; 下标“f”和“m”分别表示水和岩石,x和z为位置坐标, erfc表示互补误差函数。

在数值求解中, 岩石基质由100 m×100 m的矩形区域表示。裂隙流动换热模型验证的输入参数见表1。图3a表示不同时间沿裂隙的流体温度分布;图3b表示不同时间岩石基质中z=2.5 m处的温度分布。可以看出数值解与解析解吻合较好, 最大相对误差仅为0.8%。

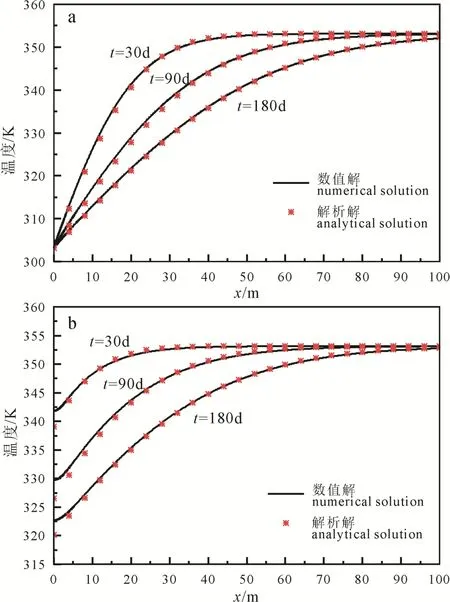
图3 裂隙流动换热问题解析解与数值解比较Fig. 3 Comparison between analytical solution and numerical solution

表1 裂隙流动换热模型计算参数Table 1 Calculation parameters of fracture flow heat transfer model

对于应力作用引起的岩石形变, 可通过 Bai et al.(2005)针对典型热固结问题提出的精确解析解进行验证。土柱热固结问题几何模型如图4所示, 土柱高度为1 m, 初始温度 283.15 K, 初始孔隙压力0.1 MPa。顶面施加0.1 MPa的垂直压力荷载, 顶面温度和压力分别为333.15 K和0 MPa, 侧边界和底部边界被视为不透水和绝热, 且位移受到法向约束。验证模型所需的计算参数列于表2中。图5表示数值计算得到的温度、孔隙压力和位移分布,可以看出, 数值解与解析解计算结果吻合很好, 验证了热流固耦合计算的准确性。

图4 土柱热流固问题模型示意图Fig. 4 Schematic diagram of soil column model

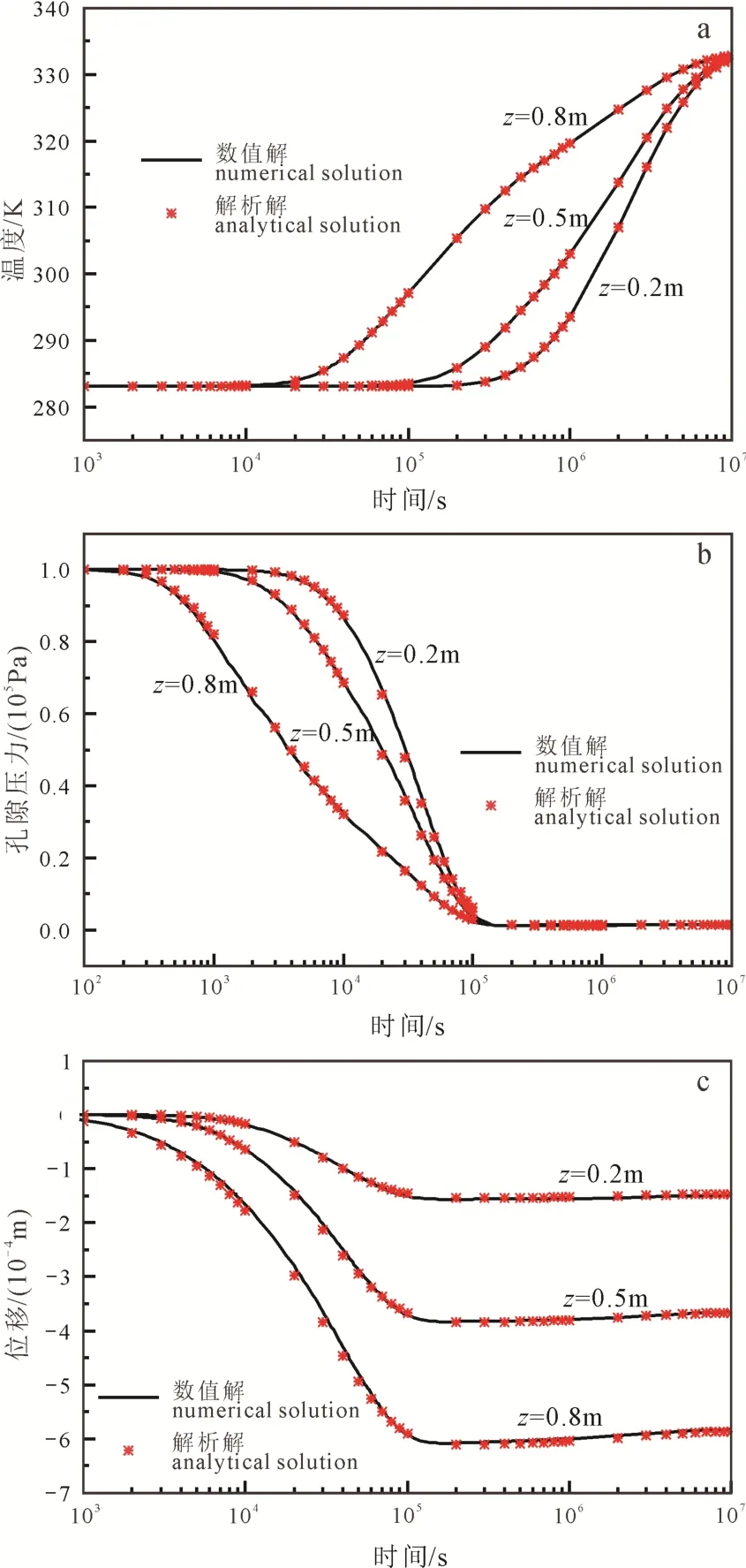
图5 热流固问题解析解与数值解比较Fig. 5 Comparison of analytical and numerical solutions

表2 热流固问题计算参数Table 2 Calculation parameters of THM problems

2 物理模型

热储模型示意图见图 6, 计算区域为1000 m × 1000 m × 1000 m 的立方体, 位于地下2200～3200 m, 模型由外部围岩、压裂储层、人工裂隙、注入井和生产井组成。压裂储层位于模型中间,尺寸为 600 m × 600 m × 500 m, 具有与外部围岩不同的参数。注采井长度均为500 m, 间距为400 m。注采井之间分布有 1条垂向裂隙和 4条水平裂隙,水平裂隙间距为100 m, 初始隙宽为2 mm, 其余计算参数见表3(Lei, 2020)。储层顶部的初始温度设为140 ℃, 温度梯度为 0.057 ℃/m, 初始压力梯度为10 000 Pa/m。计算过程中, 采出井井底压力设为26 MPa, 绝热和无流动边界条件应用于所有外部边界。

图6 储层模型示意图Fig. 6 Reservoir model diagram

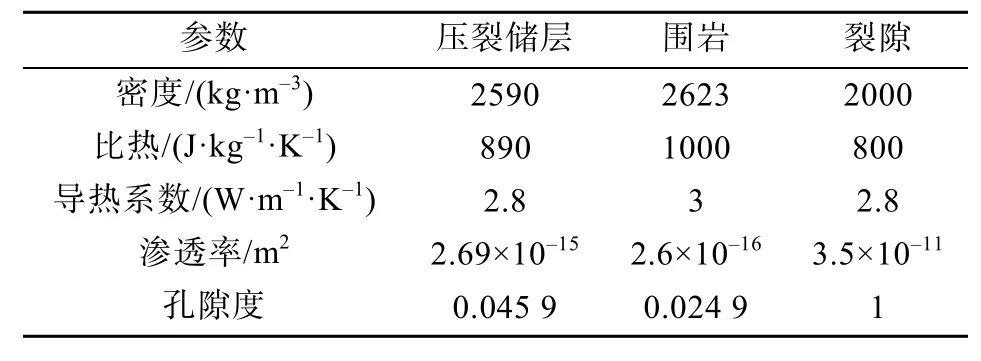
表3 储层参数(据Lei, 2020)Table 3 Reservoir parameters (from Lei, 2020)

3 结果与讨论

3.1 注入流量的影响

参考青海省共和县恰卜恰干热岩体地热地质特征, 如物理模型部分参数设定, 增强型地热 ORC系统性能分析的其他输入参数如表4所示。进行了干热岩资源开采参数及布井参数对干热岩发电系统性能的影响规律分析。注入流量对净输出功、年均净输出功和热效率的影响如图7-9所示。由图7可以发现, 5种注入流量下, 净输出功均随着时间的推移而减小。这是因为干热岩的即时热量有限, 随着地热流体提取热量的累积, 热源传递到热储层的热量无法得到及时的补充。净输出功等于膨胀机轴功减去泵功, 在同一注入流量下, 随着时间的推移,生产温度是衰减的, 导致发电系统膨胀机轴功减小;地热流体在热储中的流动造成有效应力变化, 地热流体与岩体的传热引起热应力变化, 二者均改变了储层应力分布, 造成岩体基质与裂隙变形, 导致裂隙渗透率增大, 注采压差是减小的, 导致注入泵功耗减小, 两者的综合作用造成了净输出功的变化趋势。20年运行周期内, 注入流量分别为 30 kg/s、40 kg/s、50 kg/s、60 kg/s和 70 kg/s下, 净输出功年均下降率分别为 0.57%、1.15%、1.80%、2.62%和3.73%, 下降速率随着注入流量的增大而增大。由图8可以发现, 年均净输出功随着注入流量的增大, 先增大后减小, 当注入流量为50 kg/s时, 年均净输出功达到最大值1 470.1 kW, 这主要是由衰减的生产温度和增大的注入流量综合造成的, 当注入流量小于50 kg/s时, 注入流量的增大对净输出功的影响较大, 当注入流量大于50 kg/s时, 生产温度的衰减对净输出功的影响较大。由图9可以发现, 5种注入流量下, 热效率均随着时间的推移而减小, 减小幅度是增大的。注入流量越小, 发电系统的热效率越大。20年运行周期内, 注入流量分别为30 kg/s、40 kg/s、50 kg/s、60 kg/s和 70 kg/s下, 热效率年均降低幅度分别为0.26%、0.62%、1.15%、2.62%和3.73%, 注入流量越大, 热效率的年均降低幅度越大。注入流量对净输出功和热效率具有不同的影响, 实际干热岩发电系统中要综合考量各种因素, 进行全生命周期的性能评价。

表4 增强地热ORC系统输入参数Table 4 Enhance input parameters of geothermal ORC system

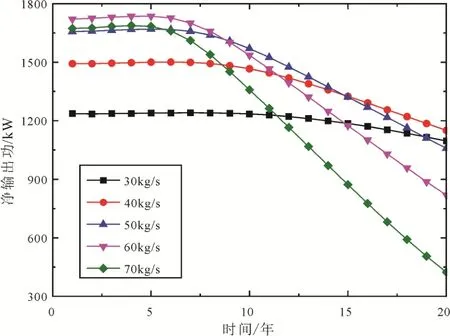
图7 注入流量对净输出功的影响Fig. 7 Effect of injection flow on net output work

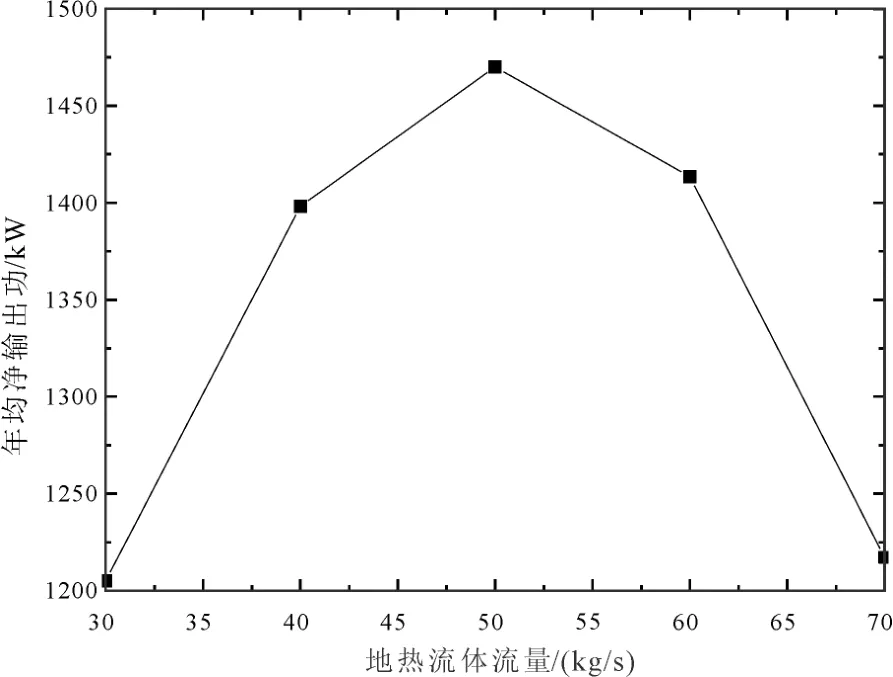
图8 注入流量对年均净输出功的影响Fig. 8 Effect of injection flow on annual average net output work

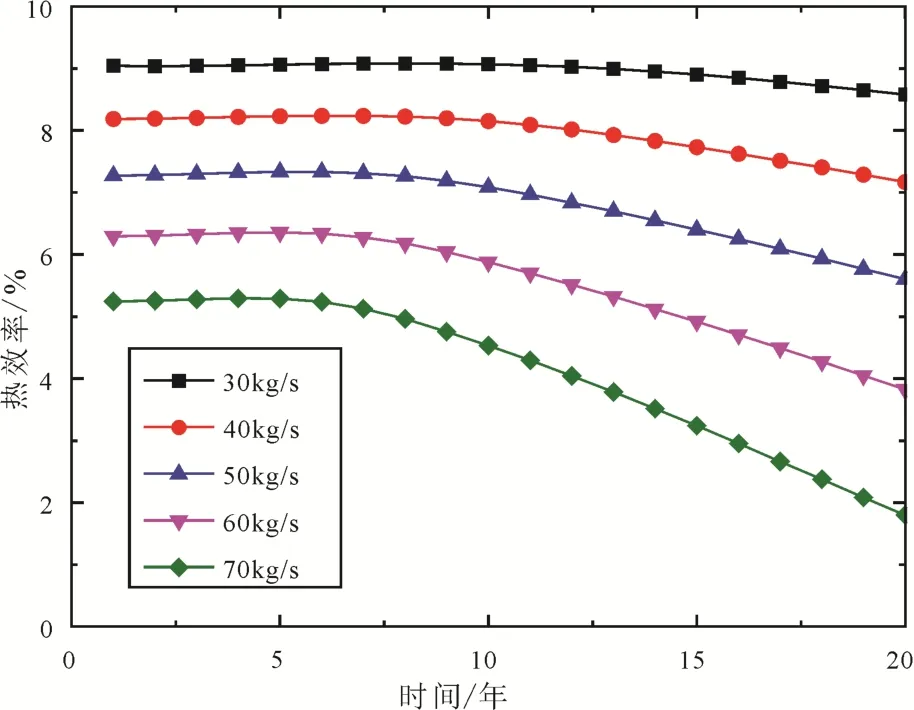
图9 注入流量对热效率的影响Fig. 9 Effect of injection flow rate on thermal efficiency

3.2 注入温度的影响

注入温度对净输出功、年均净输出功和热效率的影响如图10-12所示。由图10可以发现, 5种注入温度下, 净输出功均随着时间的推移而降低, 降低速率是增大的, 这是因为早期储层的低温区并未推进至生产井, 低温流体能在运行过程中吸收足够的热量, 造成地热流体温度随着开采年限推移不同的衰减幅度, 进而影响净输出功的时间演变趋势。20年运行周期内, 注入温度分别为50 ℃、60 ℃、70 ℃、80 ℃和90 ℃下, 净输出功年均下降率分别为2.00%、1.80%、1.70%、1.66%和1.65%。随着注入温度的增大, 生产温度的衰减速率减小, 造成发电系统膨胀机轴功衰减速率减小; 注入温度的提高使得地热流体黏度减小, 地热流体流动阻抗减小,造成注入泵功耗减小, 进而造成了不同注入温度下净输出功的时间演变趋势。由图11所示, 年均净输出功随着注入温度的增大, 先增大后减小, 当注入温度为 60 ℃时, 年均净输出功达到最大值1470.1 kW。在相同的注入流量下, 较小的注入温度可以从热储获得更多的热量, 但也会造成生产温度减小, 使得发电系统效率降低, 加之注入温度对注入泵功耗的影响, 多种因素的综合作用使得年均净输出功存在极值。由图12可以发现, 5种注入温度下, 热效率均随着时间的推移而减小, 减小幅度是减小的。注入温度越高, 热效率越大。这是因为注入温度越高, 相同运行年份的生产温度越高, 在相同的冷凝温度下的热效率越大。20年运行周期内,注入温度分别为 50 ℃、60 ℃、70 ℃、80 ℃和 90 ℃下, 热效率年均下降率分别为 1.40%、1.15%、1.01%、0.96%和 0.95%, 注入温度越高, 热效率年均降低速率越小。注入温度对热效率和净输出功具有不同的影响, 从净输出功角度考量, 基于本文的假定, 最优的注入温度为60 ℃。实际工程中, 应兼顾干热岩的开采效率与开采寿命。

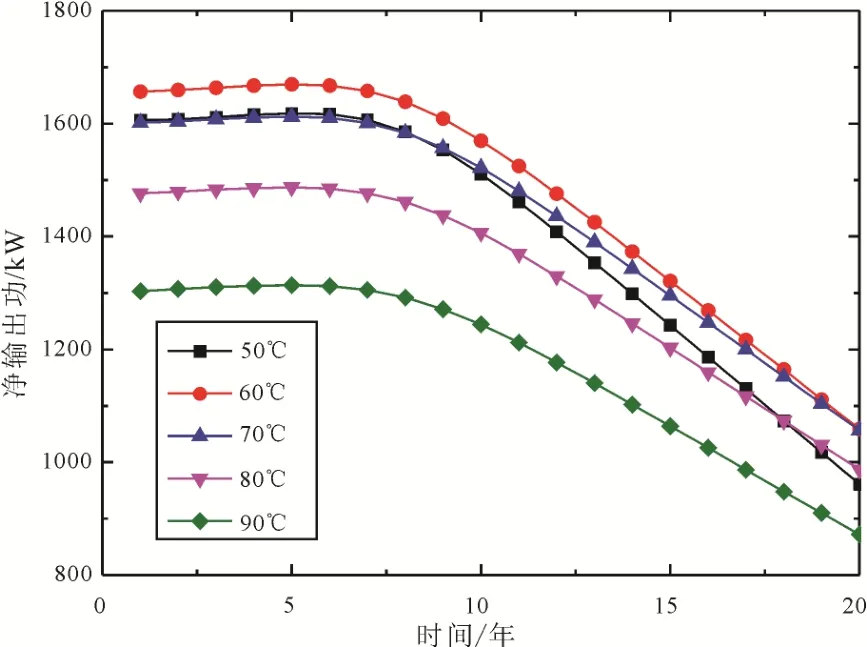
图10 注入温度对净输出功的影响Fig. 10 Effect of injection temperature on net output work

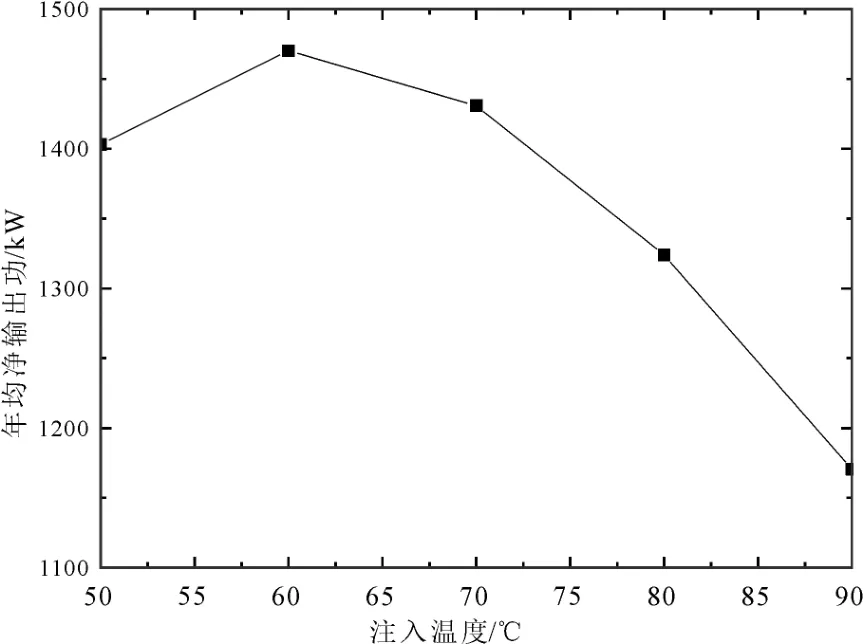
图11 注入温度对年均净输出功的影响Fig. 11 Effect of injection temperature on annual net output work

图12 注入温度对热效率的影响Fig. 12 Effect of injection temperature on thermal efficiency

3.3 井间距的影响

井间距对净输出功、年均净输出功和热效率的影响如图13-15所示。由图13可以发现, 7种井间距下, 净输出功均随着时间的推移而降低, 降低幅度是增大的, 这是由衰减的生产温度和降低的注采压差造成的。井间距分别为250 m、300 m、350 m、400 m、450 m、500 m和550 m下, 净输出功的年均下降率分别为 3.59%、3.06%、2.43%、1.80%、1.25%、0.76%和 0.39%, 这是由于井间距的增加导致储层冷锋面和低温区面积的降低, 井间距越大,地热流体在注采井间的有效换热区域越大, 等量的流体可采取的热量总量越大, 致使冷锋面与低温区的推进速度减慢, 造成地热流体生产温度衰减速率减小。由图14可以发现, 年均净输出功随着井间距的增大先增大后减小, 当井间距为450 m时, 年均净输出功达到最大值1 497.3 kW。井间距的增大使得相同运行年份的生产温度增大, 发电系统膨胀机轴功越大; 井间距的增大也使得地热流体循环在压裂储层的循环路径增大, 注入泵功耗增大, 两者的综合作用造成了年均净输出功的变化趋势。由图15可以发现, 不同井间距下, 20年运行周期内,热效率均随着时间的推移而降低, 井间距分别为250 m、300 m、350 m、400 m、450 m、500 m和550 m 下, 热效率的年均下降率分别为 2.57%、2.10%、1.61%、1.15%、0.77%、0.44%和 0.19%。从净输出功角度考量, 基于本文的假定, 最优的井间距为450 m。

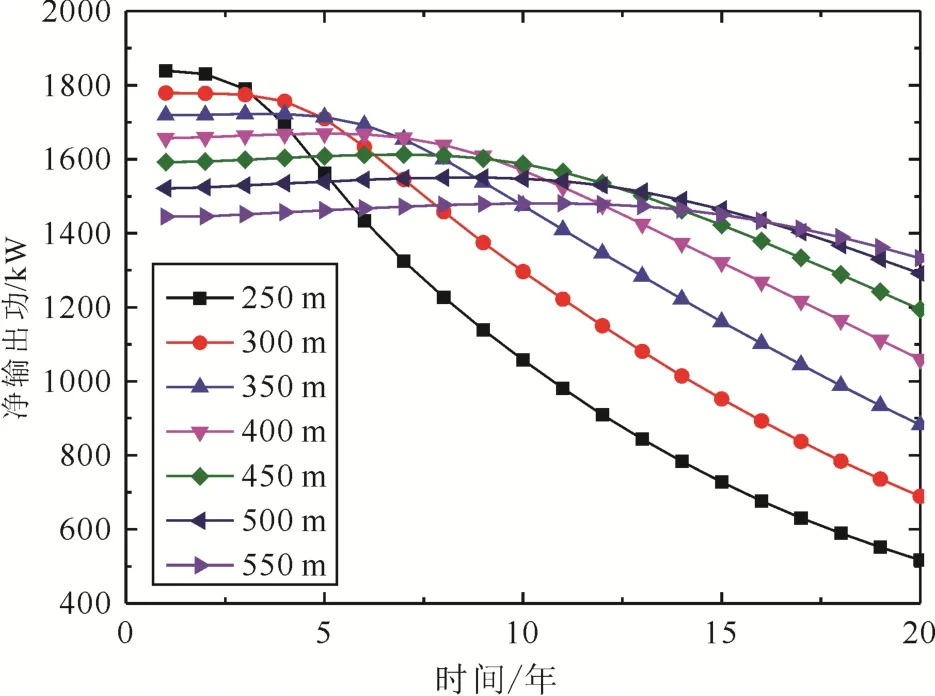
图13 井间距对净输出功的影响Fig. 13 Effect of well spacing on net output work

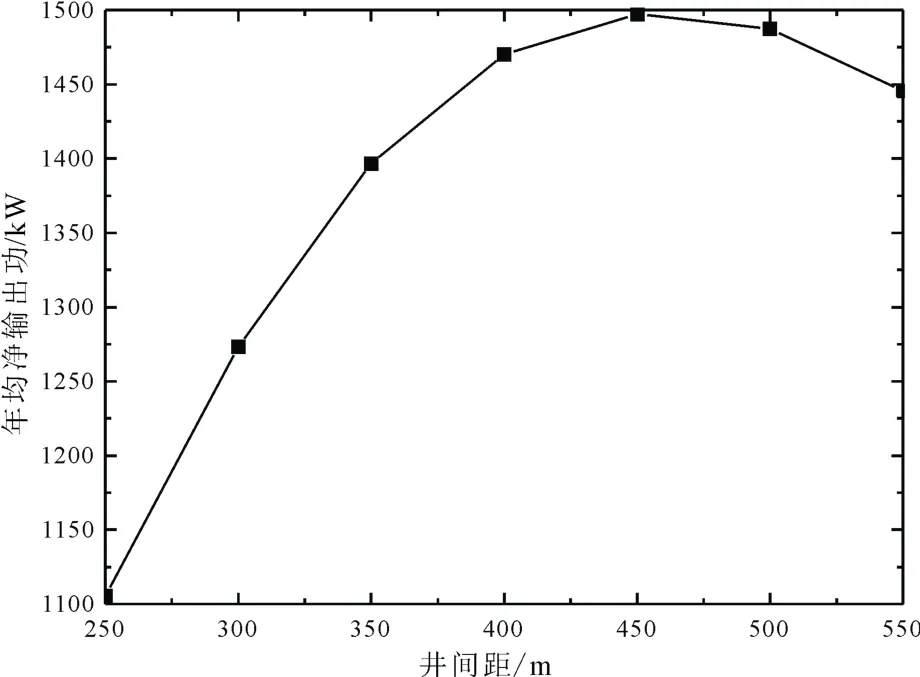
图14 井间距对年均净输出功的影响Fig. 14 Effect of well spacing on annual net output work

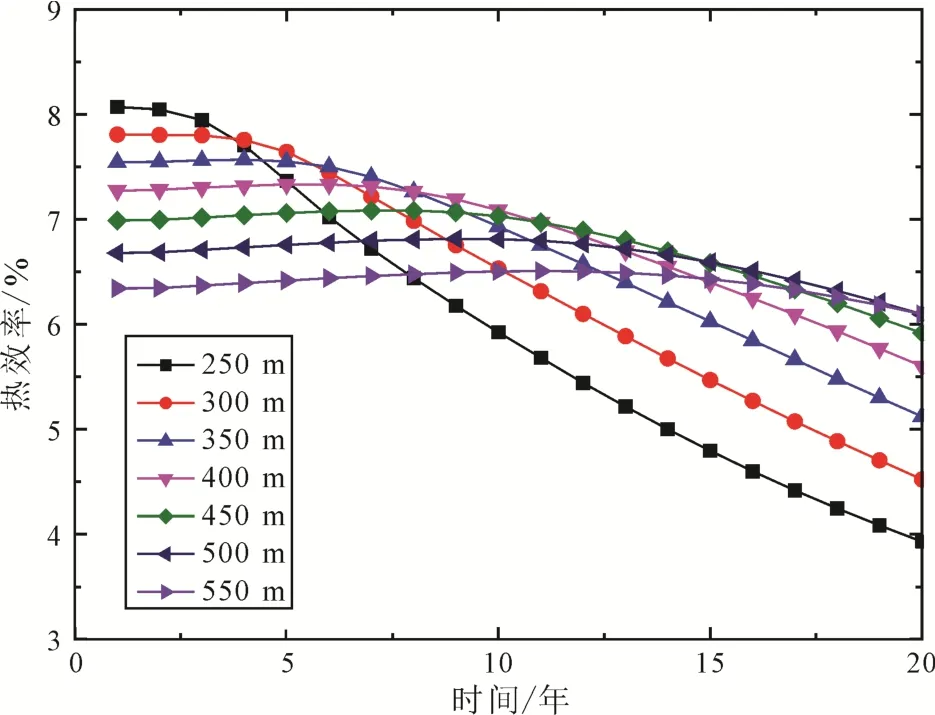
图15 井间距对热效率的影响Fig. 15 Effect of well spacing on thermal efficiency

4 结论

本文建立了耦合井筒、热储和地面发电系统的全局数学模型, 包括 THM 耦合的三维非稳态数值模型和有机朗肯循环系统工作模型, 参考青海省共和县恰卜恰干热岩体地热地质特征, 研究了地热资源开采参数、布井参数对发电系统性能的影响规律,地热流体开采参数和布井参数对增强型 ORC系统的开发效率和稳定性具有重要影响, 主要结论如下:

(1)在相同的注入流量、注入温度和井间距下,岩石孔隙压力和热应力作用造成裂隙渗透率增大,生产温度和注入泵功耗随着时间推移是减小的, 净输出功和热效率均随着时间的推移而减小。

(2)注入流量的提高使得发电系统膨胀机轴功增大, 但也会造成注入泵功耗增大, 存在最优的注入流量 50 kg/s, 年均净输出功达到最大值1 470.1 kW, 注入流量的增大造成系统热效率减小。

(3)20年运行周期内, 注入温度越高, 热效率越大, 净输出功的年均降低幅度越小, 可以延缓系统的热突破时间, 有效延长系统的运行寿命。注入温度对热效率和净输出功具有不同的影响。当注入温度为 60 ℃时, ORC系统年均净输出功达到最大值1 470.1 kW。

(4)井间距对储层热稳定性及运行寿命非常重要, 在合理的范围内增大井间距可以有效提升增强型ORC系统的效率与稳定性。但超过一定范围, 井间距对发电系统性能的改善会有所降低。井间距越小, 净输出功和热效率的年均降低速率越大, 当井间距为 450 m时, 年均净输出功达到最大值1 497.3 kW。

Acknowledgements:

This study was supported by National Natural Science Foundation of China (No. 42102336), and Natural Science Foundation of Guangdong Province (No.2021A1515011763).