焊条自动计量机构计量盘拓扑优化设计*
徐向前,杨培静
(西安石油大学 材料科学与工程学院,西安 710065)
0 引言
针对于国内焊条存储计量机构的研究短缺,焊条自动计量机构同时具备焊条存储、分类和计数功能,便于实际加工生产中工人准确拿取和仓库管理人员记录焊条情况。为了减轻焊条计量盘的重量,提高焊条自动计量机构整体性能,对焊条计量盘进行结构优化设计。目前结构优化主要有形状优化、尺寸优化、拓扑优化3个类型[1],在这3种优化设计中,拓扑优化对于结构的设计变量更多、材料优化效果更加明显、具有更大的设计空间和发展前景,拓扑优化的思想是考虑目标函数约束下计算优化设计区域的材料分布最优解[2]。对于二维壳体和三维实体等连续体拓扑优化主要有均匀化方法、基结构方法、变密度方法、水平集算法、渐变优化算法等[3]。焦洪宇、周奇才等[4]基于变密度法的体积约束下,以结构最小柔度为目标函数进行周期形拓扑优化达到了桥式起重机的轻量化;李英磊等[5]基于变密度法建立飞机隔框结构数学模型,在最优化准则方法下引入拉格朗日公式计算拓扑优化结果,总体减重了38.2%。
本文以某焊条自动计量机构计量盘为研究对象,从材料和结构等优化方面对计量盘进行了轻量化设计。确定尼龙为初始材料,以计量盘整体柔顺度为目标函数、减少30%的体积为约束条件,基于变密度法对计量盘进行了拓扑优化设计。最后对优化后的模型进行了静力学和模态分析,进一步印证了优化方案的可行性。
1 数学模型建立
变密度法[6]是以每个单元的伪密度作为常数并引入0~1的伪密度取值范围[7],建立伪密度和材料特性之间的显示函数关系,其理论公式如下:
式中:E为弹性模量;η为单元密度;E0为实际材料属性;ν为泊松比。
在实际迭代运算过程中,每个单元的材料物理属性伴随单元的密度改变发生变化,保留单元和去除单元为小于或大于接近1或0的某一特定值。但针对于模型单元中伪密度在[0,1]中间范围的数值,需要引入插值来惩罚模型解决原变密度法中仅出现0或1的离散现象。文中使用SIMP插值方法优化数学模型,优化网格依赖问题[8]使中间函数值向两边靠拢从文献[9]得知p取值为3时可方便计算算法收敛。
以密度为设计变量,体积为约束条件,结构的总柔度(刚度)为目标函数,基于SIMP插值的变密度建立拓扑优化数学模型,其公式如下:
式中:ρ为每个单元密度矢量;C为整体机构柔度;F和U分别为结构的外部载荷和位移;K为整体结构刚度矩阵;Vi和V分别为单元初始体积和优化目标体积;ρmin为单元密度值下限,ρmin一般取值为接近于0。
2 有限元模型建立与分析
2.1 初始模型建立
利用Solidworks软件建立焊条自动计量机构三维模型,图1为焊条自动计量机构。计量盘通过轴承座和安装板螺栓连接与箱体固定,其工作流程为:操作管理人员将焊条放进箱体内,机构整体通过控制电机制动带动轴和计量盘转动达到焊条存取和计数目的。为了减轻机构整体重量和电机负载,需要计量盘在达到轻量化的同时满足强度和刚度要求。图2为计量盘轴测图,具体参数:长380 mm,外径180 mm,内径150 mm,圆槽大小8 mm×φ6 mm。

图1 焊条自动计量机构装配图

图2 计量盘轴测图
焊条自动计量机构正常运转时,计量盘主要承受箱体内焊条的压力。如图3(a)所示,红色部分为初始放入焊条时计量盘受力区域,焊条实际施加的压力为Fy。结合计量盘中间翼梁为实际主要承载情况,近似将其受力分成工况1、工况2、工况3和工况4,如图3(b)所示。以工况1为例,当计量盘受力区域变成工况1所示时,通过施加F力等效Fy力的影响。箱体内初始可存放7.8 kg的焊条,即Fy=76 N,与F力夹角α=45°,经三角函数计算F值大小为108 N。计量盘承受压力随着机构运转时焊条减少而降低,为方便受力分析同时满足实际载荷施加要求对计量盘受力区域简化成全部施加F大小的均布压力,各工况的受力方向和区域为图3b箭头所指方向,大小为108 N。
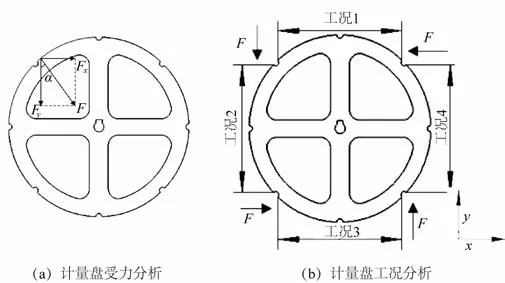
图3 计量盘受力工况图
2.2 材料属性设定
为了最大程度减轻计量盘重量,计量盘选用尼龙材料。塑性材料在进行静力学分析前需要输入其应力应变数据建立数据库,在塑性变形阶段尼龙应力和应变数据[10]如表1所示,其物理材料参数如表2所示。
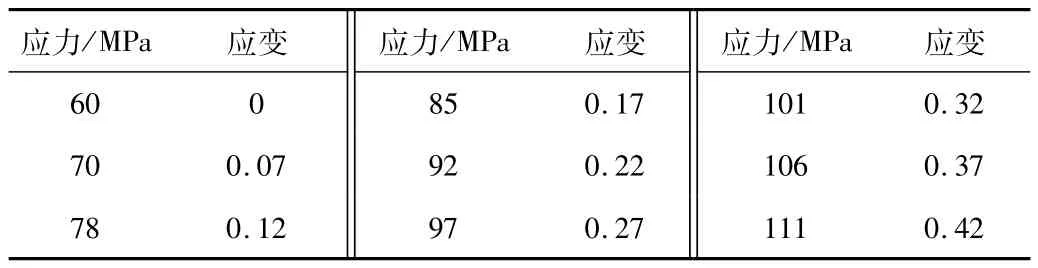
表1 尼龙应力应变数据

表2 尼龙材料属性
2.3 模型建立与分析
将计量盘模型导入Abaqus软件Part模块实体单元,选用Abaqus自带的Mesh模块进行计量盘模型网格划分。模型网格划分采用整体划分,网格类型均为六面体网格单元。为了提高网格质量和结果分析精准度,将模型分割成比较简单的区域,同时对模型进行简化:忽略计量盘圆槽、圆角等对分析结果影响不大的部分。计量盘模型网格类型为C3D8R,单元总数31 311个,网格节点数40 448个,图4为简化处理后网格划分的有限元模型。

图4 计量盘网格模型
定义模型边界条件和受载情况,以工况1为例,针对其受力方向和受力区域,通过Abaqus的Interaction模块耦合功能对计量盘耦合区域在-Y方向施加108 N大小的载荷。根据机构中计量盘运动方式对其添加转动约束,同样采取耦合方式,并在Load模块的位移/转角条件约束耦合点X、Y、Z方向全部自由度。如图5所示,图中绿色区域为受力区域,箭头A所指红色区域范围为边界条件施加区域。

图5 边界条件示意图
对计量盘模型进行有限元分析,其工况1、工况2、工况3、工况4 Mises应力云图如图6所示。

图6 计量盘4种工况应力云图
由材料力学强度理论可知,当结构中材料应力值达到超过屈服强度或抗拉强度临界值时,材料就会产生永久变形或者断裂现象,因此计量盘模型中的最大应力值应小于材料的许用应力[σ]。从图6的4种工况云图可以看出最大应力都位于计量盘中心转轴处,4种工况最大等效应力为0.023 MPa,基于Von mises屈服准则进行尼龙材料[11]的计量盘结构分析,其公式为:
式中:σr为等效应力;σ1、σ2、σ3分别为第1、第2、第3应力;σs为尼龙材料的屈服强度,取值60 MPa[12];n为安全应力系数,取值为2。
所以4种工况最大应力均满足结构刚性需求,因此可对计量盘模型进行减重优化。
其次,全面客观地介绍正面战场的积极作用。虽然由于国际国内形势等原因,对正面战场及国民政府在抗战中的积极作用在不同时期的强调有所不同,但中国共产党总的来说是采取客观态度的,党的领导人历来都有肯定。这种肯定体现在各种纪念活动中领导人的公开讲话中和活动具体安排上。
3 拓扑优化设计
3.1 优化参数确定
结合上文计量盘模型4种工况应力云图可知,除去最大应力处所在的非优化区域其余应力分布都集中在计量盘模型的相同结构区域,表3为工况1、4某同一位置的网格积分点应力值。由表3可知,两种工况下相同位置网格积分点应力值比较接近,相差最大值为0.001 5 MPa。结合数据对比结果,可将工况1的优化结果作为标准替代其他工况来方便模型计算。
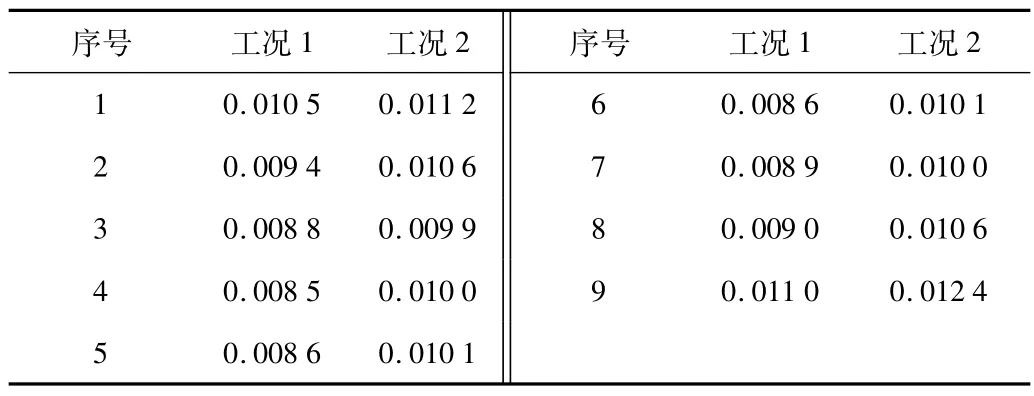
表3 工况1、4应力值 MPa
考虑到分析模型载荷的施加方式、分布区域、边界条件位置以及加工难易程度,需要选定出模型的优化区域和范围来满足模型制造和应用需求[13]。将模型所有工况受力、边界位置面和其部分连接区域限制为非优化区域,模型非优化区域如图7所示:绿色部分为非优化实体区域,红色部分为冻结表面(后视表面相同)。根据公式(2)的数学模型,以计量盘整体柔顺度为拓扑优化目标函数,在本研究中目标函数目的是使整体位移最小,而位移的一个整体度量是模型的应变能,从而目标函数最终设定为应变能最小。约束条件为减少优化区域初始体积的30%,设计变量为单位密度。设置优化目标函数变化率小于0.01%时迭代收敛,迭代次数30次。

图7 计量盘模型非优化区域
3.2 拓扑优化设计
完成优化各项参数设定后开始迭代优化。优化过程中目标函数和体积变化如图8和9所示,当迭代次数等于9时目标函数收敛柔度变化趋于稳定,同样迭代到第9次时体积约束函数收敛,总体积减小为初始体积的70%。如图10所示,计量盘轻量化设计效果明显,与工况1云应力图比较,最大Von mises应力值增加至0.157 MPa,仍满足材料安全系数要求。拓扑优化得到的模型可能不满足实际工程情况的加工制造要求,初始拓扑优化结果仍然需要人工处理[14],如消除孔洞、形状不规则和复杂边缘并进行人为重构以提高其最终设计制造能力,修改后最终的拓扑结构如图11所示。

图8 柔度变化图

图9 体积变化图
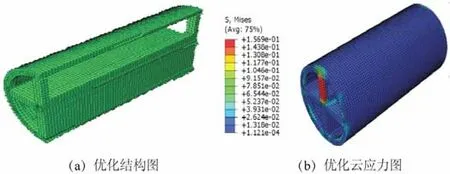
图10 计量盘拓扑优化图

图11 计量盘优化模型
3.3 计量盘动态特性分析
模态分析是研究结构动力特性的有效方法,通过模态分析,可以得到一定频率区域内各阶模态的动态特征。利用Lanczos迭代法将计量盘模型转换为有限元模型,对于离散无阻尼结构[15]的振动激励线性运动函数,在本例中计量盘模型可以表示为:
式中:M为结构质量矩阵(对称矩阵);K为结构刚度矩阵(正定矩阵);x为节点矢量位移;x··为节点加速度矢量。
由函数方程(4)可以得到一个关于n阶广义特征值的函数关系式,其式如下:
式中:ω为振动频率(λ=ω2);φ为相关特征向量。
首先进行向量逆迭代,给定一个初始向量q1,q1的2范数等于1。
对向量正交化:
由计算可知αi、βi为三对角矩阵Tn的对角元,对正交化系数αi、βi计算:
由上述公式完成迭代形成m个正交向量qi,由此可得到三对角矩阵Tm:
求解三对角矩阵Tm特征解:
求解式(5)的向量解:
利用有限元分析软件结合Lanczos迭代法计算计量盘模型优化前后的前8阶固有频率,如表4所示。由表可知,优化后的计量盘模型前8阶固有频率均有所降低,但其低阶频率远大于外界激励频率20 Hz,避免了共振现象满足模态频率要求。通过表5比较,计量盘的重量比原结构降低48.4%,相同静载荷条件下,优化后模型最大Von mises应力值增大至0.156 9 MPa,最大位移增加至3.54×10-3mm,满足刚度要求。

表4 优化前后模型前8阶固有频率
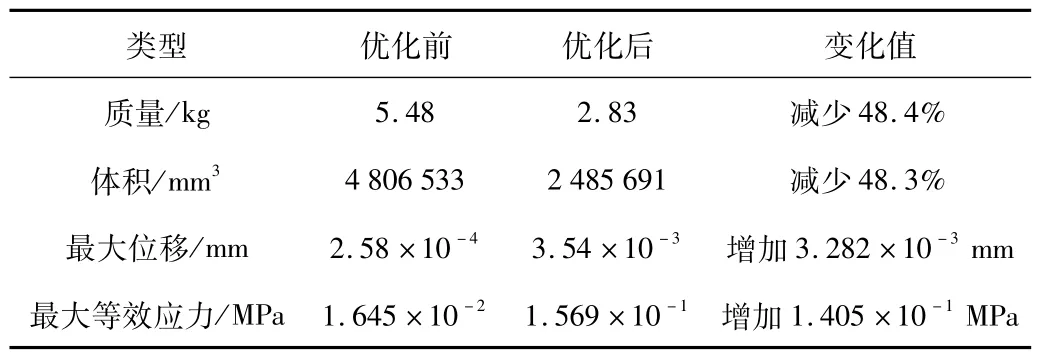
表5 计量盘优化前后比较
4 结束语
本文以焊条自动计量机构为研究对象,为达到减轻焊条箱体重量、降低电机负载的效果,对计量盘进行拓扑优化的同时保证机构性能,主要完成了两项研究,结论如下:
(1)本文在确定焊条计量盘模型在各工况下满足刚度要求的条件下,以计量盘整体柔顺度为目标函数、减少30%的体积为约束条件,基于变密度法的拓扑优化理论对计量盘模型进行结构优化。优化结果表明:计量盘模型重量比原结构减少48.4%,在不影响结构性能和完整性的情况下优化了材料整体分布,轻量化效果比较明显。
(2)对人工处理后的优化模型进行模态分析,计量盘模型优化后前8阶固有频率均有所降低,外部激励不能产生共振,优化模型满足动态特性要求。

