基于神经网络的柔性翼肋变形自感知方法研究
刘丁嘉,杨 睿
(大连理工大学机械工程学院,辽宁大连 116024)
0 引言
新一代柔性变体机翼是一种能够依据飞行器的工况,对气动外形进行自动变形调整的新型机翼,这种机翼可以显著地提高飞行器的飞行性能[1]。其中,采用了柔性翼肋的变弯度机翼是其中的重要研究方向。在飞行器的飞行过程中,这种柔性翼肋的变形情况会受到驱动载荷和气动载荷的耦合作用影响。为了对这种采用了柔性翼肋的变弯度变体机翼进行控制,就需要准确实时地感知柔性翼肋在耦合作用下的形变情况[2]。
本文以一种基于NACA0012对称翼型的鱼骨状的柔性翼肋作为研究对象。这种柔性翼肋由刚性的前缘部分和柔性后缘结构组成,其中的柔性结构由一根细长的弦向弯曲中梁和分叉的桁条作为支撑结构,支撑结构被固定到蒙皮上承载气动压力,其中的蒙皮结构采用了弹性复合材料来消除变形时出现的翘曲。该柔性翼肋可以在飞行攻角-5°~5°,飞行速度0~100 m/s的情况下工作。该柔性翼肋利用驱动系统将驱动力加载在柔性后缘的末端结构上进行主动变形,其驱动系统主要由高刚度的拉索和翼肋前端带有机械制动装置的缠绕滑轮组成,工作时,电机使得缠绕滑轮旋转并带动拉索拉动柔性翼肋末端使得柔性翼肋产生弯曲变形。其驱动力大小在0~400 N之间可调,驱动力加载方式如图1所示[3]。
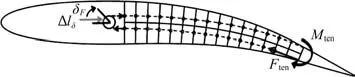
图1 驱动原理
目前的研究中,对柔性变体翼肋进行自感知的方法主要有两类。一类是通过外部测量仪器检测点或者面的空间位移从而计算变形;另一类则是通过应变片或光栅应变传感器检测结构应变从而反求变形。第一类方法中,较为典型的有李小路[4]等采用的激光测量法和韩涛等[5]采用的视觉测量方法,这两种方法分别采用了激光传感器和双目摄像头检测了机翼上散斑点的空间位移来进行变形计算。
而对于第二类方法,也有许多学者进行了研究。其中Tessler等[6]基于最小二乘法提出了一种变形反求方法,该方法通过考虑结构的力学特性可以将三维板壳的表面应变场转换为位移场。Foss等[7]基于应变模态和位移模态之间的关系提出了一种结构变形重构方法,该方法通过应变-位移转换矩阵将测得的的应变数据转换为位移数据从而反求变形。KO等[8]基于材料力学中的经典梁理论提出了KO变形反求方法,该方法通过应变与挠度的微分方程关系将测得的应变转化为挠度来反求变形。于惠勇等[9]则提出了一种利用光纤的变形重构方法,该方法利用布拉格光栅传感器获取的应变和曲率信息通过递推反求出变形情况。
然而,上述的两类方法均存在一定的问题:第一类方法中的需要测量仪器,这些仪器暴露在外接环境中,工作环境恶劣且易受到天气情况的干扰;第二类方法中则需要在蒙皮等位置上加装较多应变传感器,这会导致系统质量较大且可能不适用于柔性蒙皮等新型蒙皮。为了克服上述问题,本文提出了一种基于神经网络技术的柔性翼肋变形自感知方法,该方法可以同时综合利用由应变传感器提供的应变数据和已知的驱动力数据对柔性变体翼肋的变形进行自感知。本文提出的柔性翼肋变形自感知方法的工作过程包括两步:首先将柔性变体翼肋上粘贴的应变片采集到的结构应变数据和已知的驱动力数据利用神经网络进行处理,输出变体翼肋上下表面几个选定位移测量点竖直方向上的空间位移。然后利用变体翼肋上下表面几个选定位移测量点通过拟合的方法对柔性翼肋的变形进行自感知。
经过测试,本文在在柔性变体翼肋的上下表面及后缘处选择了7个选定位移测量点来拟合柔性翼肋变形,在柔性变体翼肋弦向弯曲中梁上均匀选择了3个位置粘贴应变片采集结构应变数据,选定位移测量点的位置如图2所示。

图2 选定位移测量点位置
本文对提出的柔性翼肋变形自感知方法的应用步骤进行详细说明,其应用步骤主要分为神经网络搭建,数据集采集,神经网络训练和自感知效果评价4个部分。
1 神经网络搭建
在应用本文提出的柔性翼肋变形自感知方法时,首先需要搭建一个能够结构应变数据和已知的驱动力数据并输出选定位移测量点的空间位移的神经网络,该步骤主要包含两步:确定神经网络拓扑结构和确定神经网络激活函数。
由于BP(Back Propagation)神经网络模型搭建方便且在处理这类关系映射领问题时有优秀的效果,本文选用该种网络拓扑结构来进行柔性翼肋变形自感知。
神经网络的输入数据由3个接触式应变传感器得到的应力数据和已知的驱动力数据组成,而所需要的输出数据则是7个选定测量点的位移数据,本文首先试着搭建了一个包含4个输入神经元和7个输出神经元的神经网络进行测试。但在对试着搭建的神经网络进行训练时发现:由于输出层神经元数量较多,为了达到可用的输出精度,该神经网络所需要的隐含层神经元数目过多,这就造成了该神经网络所需的储存空间较大且训练时间较长。因此,根据分析试验,为了在满足精度要求的情况下尽可能缩小神经网络的规模,本文中对于每一个选定测量点单独建立一个神经网络。最终,为了输出7个选定测量点的位移,本文将搭建7个具有相同的输入层与输出层结构的神经网络,该批神经网络均包含的4个输入神经元和1个输出层神经元。
在确定了输入层与输出层拓扑结构后,就需要确定隐含层拓扑结构即隐含层层数,神经元数量来完成整个神经网络拓扑结构的确定。其方式主要有剪枝算法、构造算法,交叉验证法以及试凑法等。其中,剪枝算法已经在上章中进行了详细阐述。构造算法与剪枝算法相反,是一种自下而上的算法,它以一个具有较小拓扑结构的初始网络为基础,通过逐一添加新的隐含层神经元单元最终得到所需的神经网络拓扑结构。交叉验证法是一种穷举搜索算法,它利用分割后的小部分数据集不断对各种神经网络拓扑结构进行测试直到得到最优的神经网络拓扑结构。而试凑法则是以一种粗糙的神经网络拓扑结构确定方法,该方法通过参考处理类似问题的神经网络拓扑结构通过试错的方法简单的进行几轮迭代试算,最终选出一种能够符合预期效果的神经网络拓扑结构,其含有3个隐含层,每层有30个神经元。
在确定了神经网络拓扑结构后,还需要确定神经元的激活函数。虽然在现代神经网络中,普遍采用了ReLU函数作为激活函数,但是其也存在一些严重的问题。当采用了ReLU函数的神经元输入为负值的时候,ReLU激活函数的梯度为零。在这种情况下,应用该激活函数的神经元权重无法得到更新或者也可以说该神经元将永远不再在任何的输入数据点上激活,这种情况也被称为神经元“死亡”。为了避免该种情况的发生,本文中将采用其改进型Leaky ReLU函数作为隐含层激活函数[10]。Leaky ReLU的函数表达式如下所示:

2 数据集采集
在建立了神经网络模型后,就需要利用仿真,获取数据集训练神经网络以及最终评价这种柔性翼肋变形自感知方法。
柔性翼肋的变形会同时受到驱动载荷和气动载荷的影响。为了对其变形情况进行研究,本文将选取一些工况,借助有限元软件对其进行仿真分析。首先,对该柔性翼肋进行建模并利用有限元软件模拟出该柔性变体翼肋在工作区间内不同工况下受到的气动载荷,然后将气动载荷与已知的驱动载荷一起加载到柔性翼肋结构上,就能够得到7个选定位移测量点的位移数据以及弦向弯曲中梁上3个应变片粘贴点处的应变数据,仿真结果如图3所示。其中,1号选定位移测量点所对应的数据集结构示意如表1所示,其余6个选定位移测量点所对应的数据集与之类似。

图3 仿真结果示意图

表1 位移测量选定点1号的数据集结构示意
得到仿真数据集后,将其按照80%、10%、10%的比率划分为训练集、验证集和测试集分别用于神经网络的训练、验证和柔性翼肋变形自感知方法测试评价。
3 神经网络训练
在确定了训练集、验证集和测试集后,就可以开始对神经网络进行训练。训练过程中,首先需要确定神经网络的学习算法。神经网络的学习算法实际上是一类利用梯度下降原理最小化误差的优化方法,其主要包括梯度下降法、Momentum法、RMSprop法以及Adam法等。
Momentum法(动量法)是为了“之字形”下降问题而提出的一种学习算法。这种方法通过引入“动量”的概念,即下降的方向是由本步计算出的梯度和前几步中计算出的梯度共同决定。这种方法的直观效果就是当前下降方向不再高度敏感于本步计算出的梯度,减少了“震荡”的情况。RMSprop法是为了解决在接近极小值时收敛速度缓慢的问题而提出的一种学习算法,它改进自另一种.AdaGrad算法,能够适用于非凸条件下的优化问题。这种方法通过计算出的梯度对学习率进行动态调整,能够在梯度不“陡峭”的情况下使用较小的步长来更加平滑的接近目标。而Adam法结合了Momentum法以及RMSprop法的优点,通过同时考虑下降方向以及下降步长,能够加快收敛并减小震荡,且对超参数的选择具有一定鲁棒性,不容易陷入局部最优的情况。经过试验对比可明显发现其比其余学习算法效果更好,因此本文中选取Adam法作为学习算法
然后将训练集上的数据输入搭建完毕的神经网络结构中对其进行训练并使用验证集测试其是否产生过拟合现象。在本文中,由于神经网络的规模较小,在训练中产生了过拟合现象,因此需要对其进行抑制。过拟合的抑制方法主要有可以采取提前停止法,正则化法以及dropout法等。
其中,dropout法的工作原理则是在神经网络的每次训练的时候都让随机的一部分神经元失活,以此来防止神经网络的输出过于依赖性某些神经元。由于单个神经网络神经元学习到的特征是随机的,不再过于应付于某几个上一层的神经元,使得训练完成的神经网络更具鲁棒性。由于该方法实现方便且在用于本文所采用的全连接神经网络上时的效果十分显著,因此本文选择dropout法进行过拟合的抑制。
在选择好了神经网络的学习算法和过拟合的抑制方法,然后就可以继续通过动态调整学习率对神经网络进行训练了。通过不断迭代学习过程,使得神经网络在训练集上达到一定的输出精度,得到一个训练好了的神经网络。其中,用于评价神经网络输出精度的目标损失函数值在训练过程中的变化示意如图4所示。
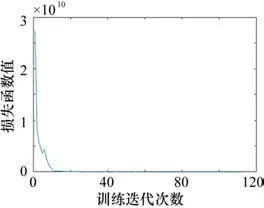
图4 神经网络训练过程
训练完成后经过验证,神经网络在训练集及验证集上的输出精度较为接近,即其不存在明显的过拟合现象,可以被用于输出选定位移测量点竖直方向上的空间位移对进行柔性翼肋变形进行自感知。
4 自感知效果评价
为了对这种柔性翼肋变形自感知方法的效果进行评价,本文用测试集数据模拟应变片传入的应变数据测试该方法的感知精度。在评价中,本文将柔性翼肋被划归成测试集的变形仿真结果作为真实值,变形自感知结果与其之间的差异为该自感知方法的误差。
由于最终自感知出的柔性翼肋变形情况是由翼肋上下表面7个选定位移测量点拟合得到的,因此本文将首先对比在翼肋上下表面7个选定位移测量点处的误差。在测试数据集上,计算机仿真位移结果和神经网络输出结果的绝对误差小于0.42 mm,相对误差小于6.00%。7个选定位移测量点的绝对误差和相对误差分别如表2~3所示。
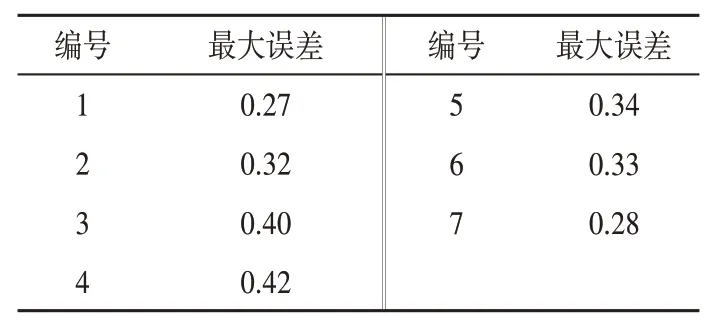
表2 选定位移测量点处神经网络绝对误差

表3 选定位移测量点处神经网络相对误差
对比柔性变体翼肋仿真出的变形曲线与通过选定选定位移测量点拟合出的自感知变形曲线之间的误差,由于测试集数据较多,因此本文选择通过绘制误差区间的方式展示这种柔性变体翼肋自感方法的误差。由于自感知得到的变形曲线是由选定位移测量点拟合而成,因此可以认为该种柔性翼肋变形自感知方法的最大相对误差与选定测量点处的最大相对误差相同,即该柔性翼肋自感知方法的最大相对误差也约为8.20%。其中,柔性变体翼肋上表面的变形自感知误差区间如图5所示,其中的虚线部分是仿真出的柔性变体翼变形曲线,而实线部分则是根据神经网络预测误差极值所拟合出的误差区间的上下限,下表面的变形自感知误差区间与之类似。

图5 柔性变体翼肋上表面自感知误差区间示意图
5 结束语
本文提出的柔性翼肋变形自感知方法基于神经网络技术,采用了神经网络技术,充分运用所在柔性翼肋上所采集的应变值和驱动力值,准确地描述了柔性翼肋在同时受到驱动力和气动力情况下的变形状态。经过仿真验证,其自感知误差小于8.20%,满足实际工程需求。
与其他应用应变传感器反求变形的方法相比,本文提出的柔性翼肋变形自感知方法具有如下优势:
(1)传感器布局在柔性翼肋上,避免受气动作用力和蒙皮弹性变形的干扰;
(2)可以充分利用驱动力大小的数据获得较为准确的结论;
(3)对比其他的将传感器布局在机翼翼面上的变形反求方法,可以用使用较少的传感器达到效果。
在本文研究的基础上,可以利用循环神经网络结构对柔性变体翼肋的变形自感知,更好地反映其在变体飞机机动时的变形情况;也可以综合考虑变体机翼内部的多个柔性翼肋变形的互相影响,更好地反映变体机翼的扭转等变形趋势。

