特征区域最近点迭代地表移动分析算法

蔡来良 康洪跃 杜 庄 张志斌

(1.河南理工大学测绘与国土信息工程学院,河南 焦作 454003;2.中国南水北调集团中线有限公司渠首分公司,河南 南阳 473000)

近年来,三维激光扫描技术逐渐在高效率获取空间立体信息应用中占据主要地位,成为地理空间数据获取的一种重要的技术手段[1]。三维激光扫描技术在我国矿山测量领域得到了大量研究和应用,特别是在露天开采边坡监测、露天矿储量管理、井工开采边坡监测、采空区安全监测、地表沉陷监测等方面应用较为广泛[2]。相较于传统的全站仪、RTK等方式,三维激光扫描技术具有扫描速度快、数据获取全面等优点,尤其是在悬崖、边坡等危险地点,该技术可以实现无接触测量,有助于确保测量人员安全。国内许多学者在基于点云的地表变形分析方法方面取得了丰富的研究成果,大致有点云直接对比求取变形法、点云模型对比求取变形法、点云特征点线提取变形法这3类方法。

在点云直接对比求取变形的研究方面,刘昌军等[3]通过对Hausdorff距离算法进行改进,提出了基于八叉树结构的点云与点云的精细直接比较算法,实现了变形区域多个点云数据的自动比较。王海城等[4]提出了一种基于两期点云直接计算变形的新方法,即通过对扫描点云进行特征分割、坐标变换与投影、格网划分、最短坐标距离计算与排序、中位值段取平均以及逆变换等一系列处理过程后,最终得到整个变形体高密度监测点的变形值。陈弘奕等[5]针对点云数据的特点,提出了点云和点云直接比较变形分析方法,采用最佳拟合面法来提取变化信息。魏振全[6]采用三维激光扫描仪与全站仪相组合的测量方法,对田陈煤矿某工作面上方地表移动和建筑物变形情况进行了监测和分析,获取了控制点三维坐标,进而求取了变形量。

在点云模型对比求取变形算法方面,柏雯娟[7]基于矿区的两期三维激光扫描数据,利用Kriging算法分别建立了矿区地表下沉盆地数字高程模型,对矿区地表沉陷进行分析,最后选取矿区若干有代表性的监测点的开采沉陷监测值与对应的水准测量结果进行了对比分析。于海洋等[8]在LiDAR DEM精度与不确定性分析的基础上,利用模糊推理方法建立了基于坡度、点云密度和地表粗糙度的误差相关表面,用于差值DEM不确定性的量化与DEM最小变化阈值探测,采用基于权重滤波窗口的贝叶斯估计判定与修正,较精确地获取了研究区地表形变信息。吕志鹏等[9]获取了变形体变形前后的点云数据,并利用移动最小二乘法进行了均匀格网拟合内插来提取变形信息。孟万利等[10]以相同网格划分开采前后点云数据,再利用改进的反距离权重法插值求取网格节点坐标,匹配相同网格节点作为同名点并求取下沉量,最后获取了下沉曲线与下沉DEM。梁周雁等[11]对DEM模型求差法和Hausdorff距离法计算的监测结果进行了比较分析,验证了两种方法在地表变形监测中的优势。王堃宇等[12]采用三维激光扫描技术实现了对某边坡位移的监测,获取了整个边坡的三维模型及位移云图。何荣等[13]采用S-G滤波对点云数据进行去噪处理,建立了沉陷区三维数字高程模型,利用局部表面拟合方法求取了特征点法向量,计算了地表变形前后法向量的变化量,并与特征点真实倾斜角进行了对比分析。杨帆等[14]通过对点云数据进行处理,形成了相应时段的尾矿边坡三维模型,采用等高线比较、三维质检软件比较等方法,提取了边坡变形数据。刘卫南等[15]将离散的三维点云转化为二维的密度图像,再利用粒子图像测速技术分析了位移前后两幅点云密度图像的相关性,从而计算了栅格图像中各子集的相对位移值,得到了目标区域的平面位移场。卢遥等[16]通过对矿区两期点云数据提取的DEM作差运算,得出该段时期内地表的垂直位移量,而后通过设置高差阈值和面积阈值,并采用基于高差分析方法,提取了地表沉陷信息。何倩等[17]利用地面三维激光扫描点云数据构建高分辨率、高精度DEM,再由低分辨率SRTM DEM内插补充数据缺失区域以获取整个研究区域的DEM,最后将其与高分辨率SAR影像进行时序差分处理,获取矿区地表动态沉降监测数据。

在基于点云特征点线提取变形的研究方面,张小青[18]通过提取变形监测点的三维坐标信息,进行多期数据的监测点坐标信息比较,获取了局部的变形信息。徐进军等[19]根据确定的边界,对点云进行网格分割并通过基于最短距离取“中位值”的变形计算方法,大致确定了同名变形部位,最后利用该部位的两次扫描点云来提取同名变形点,并计算其变形。司梦元等[20]设计了一套基于边坡的永久性三棱锥作为控制点,通过各期点云数据中三棱锥特征提取相应控制点,运用算法程序处理从而提取了边坡变形信息。赵不钒等[21]针对地面三维激光扫描技术在变形监测中的应用需求,结合点云序列特征,提出了利用点云特征要素提取变形信息的方法。李强等[22]选取了研究区变形特征明显的墙体作为特征点提取对象,通过提取两期墙体特征点坐标值,获得了研究区的典型特征点变形结果,并提取了研究区Z轴方向剖面线,可直观地反映出地面沉降线性变形特征。吕宝雄等[23]利用地面三维激光扫描技术提取了崩塌滑坡灾害体特征点三维坐标、虚拟断面线,通过点、线、面的综合分析,可获得灾害体的局部细节和整体位移量信息,实现对灾害体的变形监测。

上述分析表明,近年来利用三维激光扫描技术监测地表移动的研究取得了显著进展,但还存在一定的不足。例如:在利用三维激光扫描仪开展变形监测时,在缺乏人工标靶的情况下,无法准确采集到同名点坐标。本研究对此进行了相关探索,提出了同名特征区域概念,建立了特征区域最近点迭代地表移动分析算法(Surface Movement Analysis Algorithm Based on Feature Region Iteration Closest Points,FRICP),并通过试验分析验证了该算法的可行性。

1 特征区域最近点迭代地表移动分析算法(FRICP)原理

为保证观测人员安全并提高工作效率,采用三维激光扫描仪测量山地陡坡的地表地形,并通过对比多期观测数据,分析地表移动。由于每期扫描激光发射方向不同,无法在各期观测值中找到相同观测点,进而也无法使用常规的定点观测数据处理方法计算地表移动。为了克服多期观测无同名点这一技术难点,本研究将山区地表分布的岩石、树木等地物视为特征区域,构建同名特征区域提取算法;并在此基础上建立多期同名特征区域的匹配算法,最后利用ICP算法分析同名特征区域的地表移动量,算法流程如图1所示。

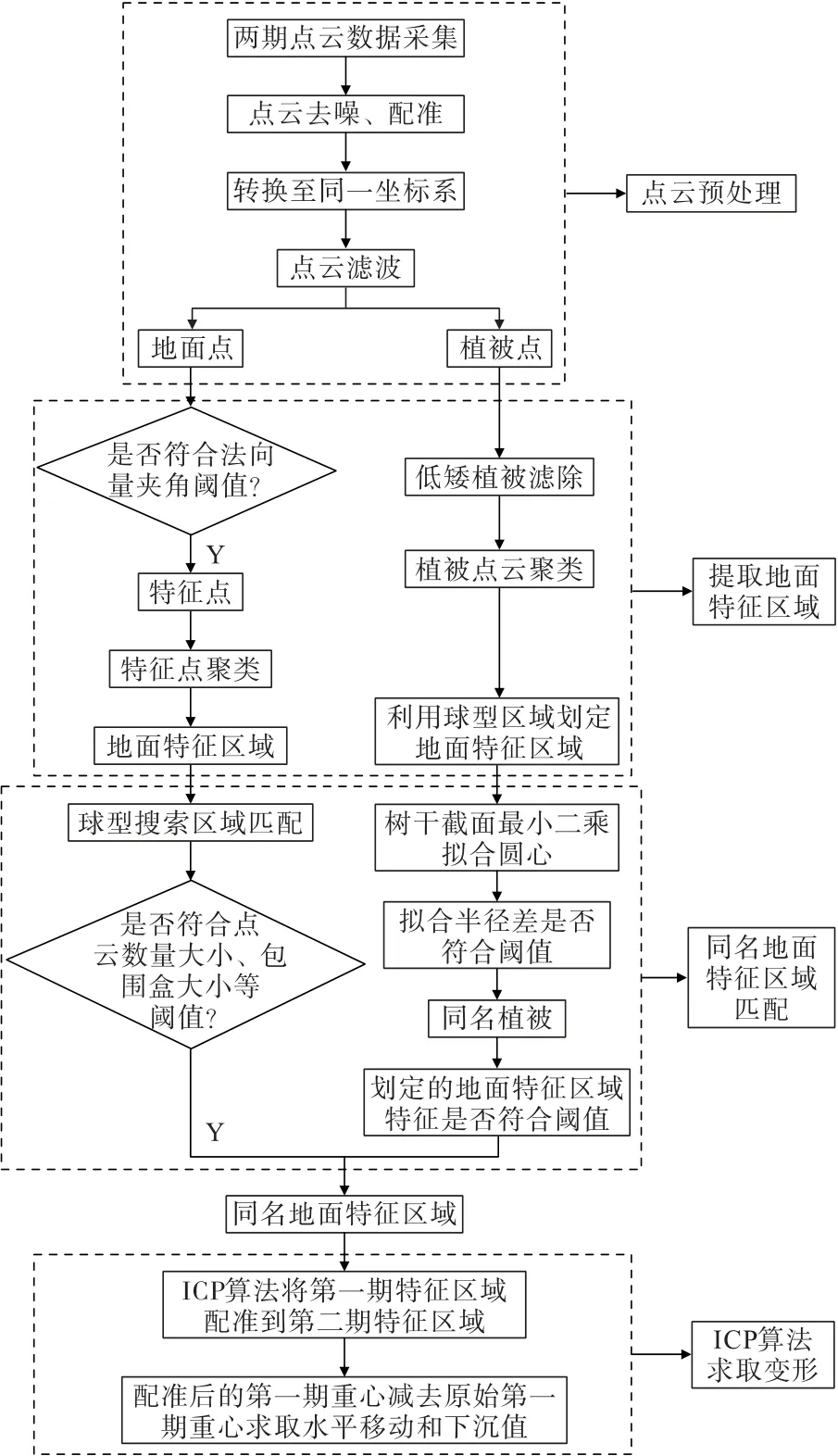
图1 FRICP算法流程Fig.1 Flow of FRICP algorithm

1.1 点云数据预处理

使用地面三维激光扫描仪获得的数据无法直接进行变形分析,需进行点云的预处理,主要步骤如下:

(1)点云去噪。将点云中的噪声点去除,降低噪声点对后续分析影响。

(2)点云配准。对采集的第一期和第二期的多站点云数据进行配准,建立完整的测区点云。

(3)两期数据坐标转换。以第一期配准后的点云数据坐标系统为基准坐标系统,将第二期配准结束的点云数据坐标转换到基准坐标系统。

(4)点云滤波。将第一期点云数据和第二期的点云数据进行滤波,分离地面点和非地面点,为提取同名地面特征区域做准备。

1.2 地面特征区域点云提取

山区地表起伏较大,与平原地区相比,地表特征十分明显。在点云中提取特征区域可为形变分析奠定基础。

1.2.1 使用地面点云提取地面特征区域

地表点云法向量是描述地表凹凸起伏的关键几何参数。平坦地区的点云法向量变化较小,非平坦区域(特征区域)的法向量变化较大,如图2所示。可以利用该点的法向量与周围点法向量的夹角和的平均值来判断该点是否为特征点,如果该点法向量与邻域内其他点的法向量夹角和的平均值较大(设置角度阈值为20°),认为该点是特征点;反之,该点不是特征点。

图2 不同地形的点云法向量Fig.2 Point cloud normal vectors of different terrains

经过法向量关系提取出的特征点离散性强,没有建立聚集关系,无法形成特征区域。本研究采用一种基于密度对噪声鲁棒的空间聚类算法(Density-based Spatial Clustering of Applications with Noise,DBSCAN)来进行点云聚类。该算法流程如下:

(1)读入点云数据,设定初始参数邻域半径为0.1,最小邻域点个数为6。

(2)遍历所有点云数据对点云进行邻域计算,若某一点邻域的个数大于最小邻域点个数,则认为该点为核心点。

(3)如果点q在核心点p的邻域内,则称点q和点p是直接密度可达的。如果存在数据点集p1,p2,…,pn是从点p1出发直接密度可达的,则称点pn和点p1是密度可达的。任意选取一个核心点找出由其密度可达的所有点云数据,生成点云簇。

(4)迭代执行上述步骤,直到所有的核心点都计算完为止。

DBSCAN算法流程如图3所示。

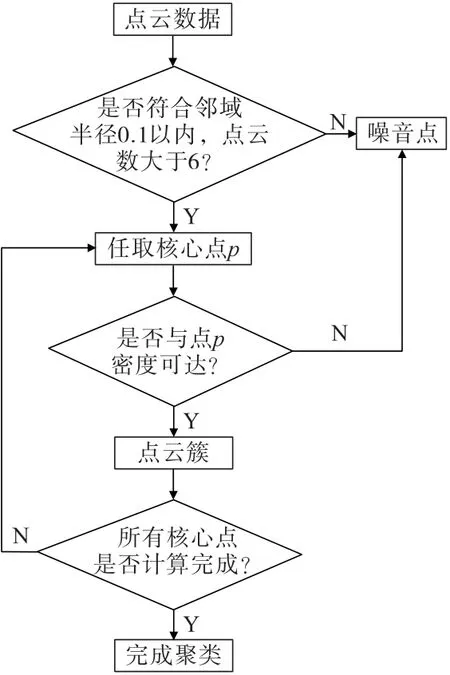
图3 DBSCAN聚类流程Fig.3 Flow of DBSCAN clustering

聚类效果如图4所示。地面特征点聚类完成之后就形成了带有聚类属性的特征区域,不再是离散的特征点。

图4 DBSCAN算法聚类效果示意Fig.4 Schematic of the clustering effects by DBSCAN algorithm

1.2.2 使用植被点云提取地面特征区域

山地测区除了地形特征明显之外,植被信息也十分丰富。本研究将树木视为天然地面标靶,对其邻近范围地面进行标定。详细步骤为:首先采用滤波算法获得植被点云;其次设置高程阈值分离低矮植被;然后对高大树木进行单木分割,获得高大树木根部附近的点云;最后对点云进行聚类,树木聚类效果如图5所示。以树根点云上一点为球心,r为半径画球,球内所包含的地面点云即为树木所标识的地面特征区域。

图5 植被点云聚类示意Fig.5 Schematic of vegetation point cloud clustering

1.3 同名特征区域匹配

获得各期监测的特征区域之后,对多期特征区域进行同名匹配,找到不同观测时期数据中的相同观测目标。下文分别探讨地面特征区域和树木特征区域的同名匹配算法。

1.3.1 地面点云提取的同名特征区域匹配

首先求出第一期地面特征区域的重心,然后以第一期地面特征区域的重心为球心,以1.2～1.5倍最大变形预计量为半径,搜索第二期地面特征区域重心。搜索到第二期区域内重心点后,对所有出现在该搜索区域内的地面特征区域求其特征度(点云数量、包围盒大小等),分别与第一期地面特征区域的特征度进行对比分析。若存在符合阈值的第二期地面特征区域,则认为该特征区域为同名区域,并将该区域点云记录下来。

1.3.2 使用树木点云进行同名地面特征区域匹配

树冠随季节变化而变化,树干在横向上生长缓慢,树干在水平方向上比较稳定且接近圆形,可以作为匹配的依据。使用距地面0.5倍树高的水平截面截取树木,对该截面内的树干点云利用最小二乘法拟合圆,利用拟合的圆心和半径匹配同名植被。首先以第一期植被点云拟合得到的圆心为搜索圆心,以r为搜索半径,建立圆型搜索区域;再将第二期的植被点云数据拟合求得的圆心放到第一期数据中,利用圆形搜索区域进行同名点匹配;最后将第一期和第二期的半径作差,并设定阈值,如果符合阈值,则认为是同名植被。

以拟合的截面圆心为球心,以大于截面高度的长度为半径画球,球内包含就是植被点云所标注的地面特征区域。对两期同名植被所标注的地面特征区域进行特征度比较,例如点云数量、包围盒大小等,如果符合阈值,则保留。

1.4 利用ICP算法进行变形分析

1.4.1 ICP算法原理

ICP算法是在源点云P中选取点pi集,在目标点云Q中找到对应的邻近点qi集,找到并由此解算旋转矩阵和平移矩阵,使得误差函数值最小,并将旋转矩阵和平移矩阵用于源点云中的点集,得到新的对应点集,计算新的对应点集和目标点云中点集的平均距离,直到平均距离小于某一给定的阈值,或者迭代到一定的次数,即可完成配准。ICP算法配准流程如图6所示。

图6所示的旋转矩阵R中,α、β、γ分别为沿X,Y,Z轴的旋转角度。

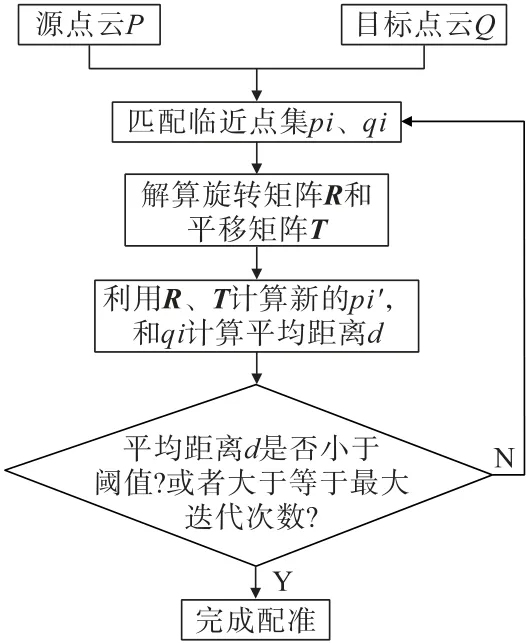
图6 ICP配准流程Fig.6 Flow of ICP registration

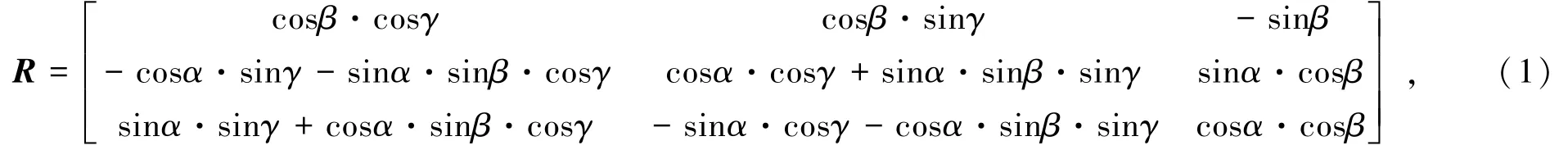
平移矩阵T为

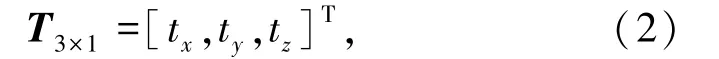
式中,tx,ty,tz分别表示沿Z,Y,Z轴的平移量。

误差函数E(R,T)为

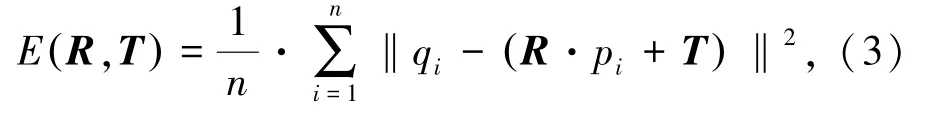
式中,n为最邻近点集个数;pi为源点云点集pi中一点;qi为目标点云点集qi中与pi对应的最近点;R为旋转矩阵;T为平移矩阵。

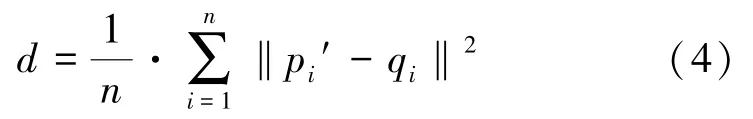
式中,pi′为源点云点集中经过旋转和平移矩阵计算后的新源点云点集;pi′为新源点云点集中的一点;d为新源点云点集pi′与对应点集qi的平均距离。

1.4.2 变形量计算

ICP算法共有5个参数,分别为源点云、目标点云、距离阈值、粗配准的初始变换矩阵(旋转矩阵和平移矩阵)以及迭代次数。如图7所示,源点云设置为第一期点云特征区域C1,目标点云为第二期对应的同名点云特征区域C2,距离阈值设置为1.5。由于两期点云已经统一了坐标系,不存在旋转变换,所以初始变换矩阵中的旋转矩阵为单位矩阵,平移矩阵为两期点云特征区域的重心值相减组成的3×1列矩阵,迭代次数默认为30次。运用ICP算法进行配准时,将第一期的点云特征区域C1配准到第二期的同名点云特征区域C2上,用配准后的第一期数据的地面特征区域C1′的重心(x′,y′,z′)减去C1区域的重心(x,y,z),该差值(Δx,Δy,Δz)即为C1区域的位移值。特征区域位移前后的重心坐标差值既可以作为ICP算法的初始平移参数,又可作为下沉和水平位移量的计算依据,是本研究算法中重要的几何参数。

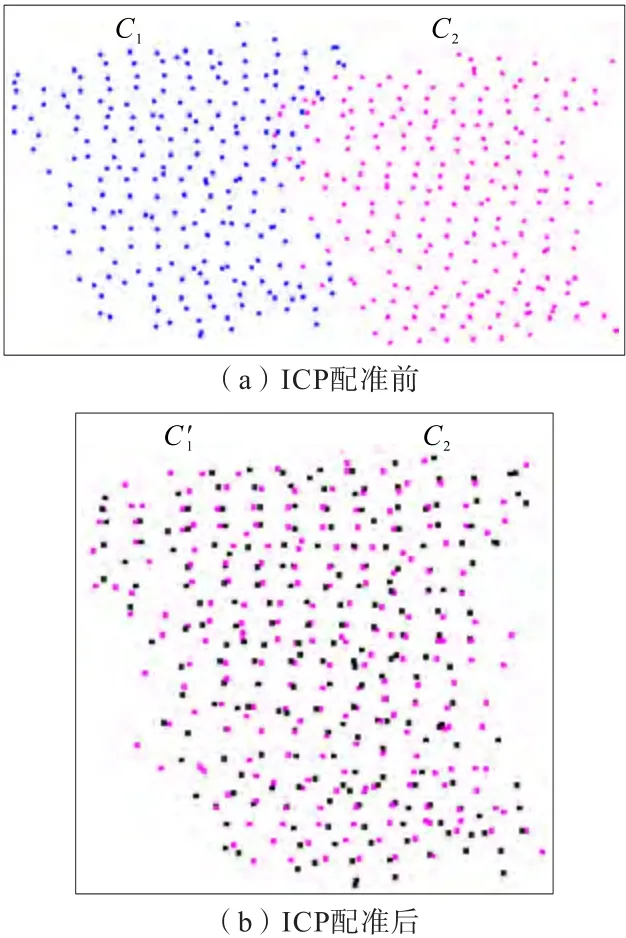
图7 特征区域ICP配准前后对比Fig.7 Comparison of the feature area before and after ICP registration

求出地表多个特征区域的位移值后,可绘制地表移动等值线图,求取地表形变场。本研究算法基于Python语言,引入Open3D库编程实现,完成点云数据处理系统开发。

2 实例分析

2.1 试验数据采集

本研究以沁水煤田2301工作面采空区上方的边坡为例进行分析,边坡长约29 m,宽约28 m,最大高差约16 m,边坡较为陡峭,坡度约35°。边坡表面植被茂盛,大多数为杂草和树木,地面起伏高低不平,石头等杂物比较多,边坡中下部坡度变化较大,且有类似台阶状的陡坎,上部坡度变化平缓。地下煤炭资源开采引起该边坡发生沉陷和水平移动。采用RIEGL VZ-1000型地面激光扫描仪,对区域进行了变形前后两期扫描,如图8所示。

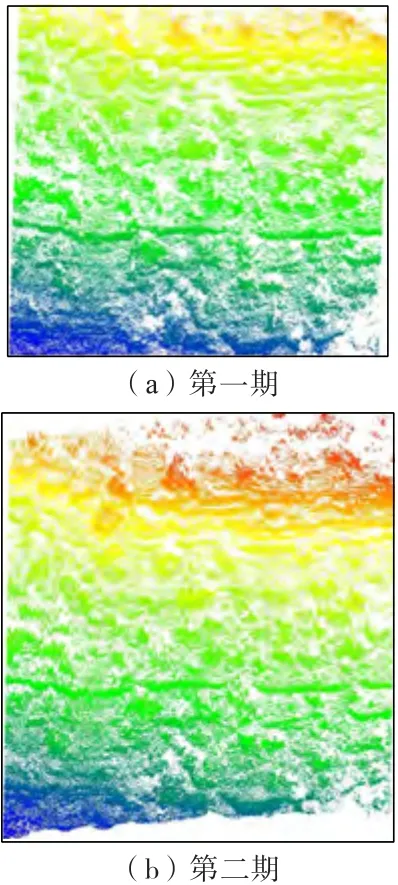
图8 两期观测结果Fig.8 Observing results of two periods

2.2 地面点云特征区域提取及匹配

首先,对两期点云进行去噪、配准以及坐标转换和滤波,为后续变形分析做准备。然后,基于法向量对地面点云进行特征点提取,以某一点为圆心,以半径0.8 m以内的点作为该点的邻域,进行平面拟合,求取该点的法向量与邻域内点法向量的夹角和的平均值,并设置夹角和阈值为20°。第一期地面点云特征点提取出25 130个,第二期地面点云特征点提取出19 889个。基于DBSCAN算法对地面点云进行了聚类分析,结果如图9所示。

图9 地面特征区域聚类结果Fig.9 Region clustering results of ground feature region

以第一期地面特征区域的重心为球心,建立球型搜索区域搜索第二期的地面特征区域,其中搜索半径设为2 m,点云数量差设为30,包围盒大小为0.2 m。基于地面点云共搜索到8对同名特征区域。

2.3 植被点云特征区域提取及匹配

将植被点云进行低矮植被滤除之后,保留的植被点云基本都是高大的树木点云。在此基础上,基于八邻域的搜索方法进行了植被点云聚类,结果如图10所示。

图10 植被点云聚类结果Fig.10 Clustering results for vegetation point clouds

以0.8 m高度、0.03 m厚度的圆柱去截取树干,将得到的植被点云进行最小二乘拟合,求取半径和圆心。以同样的方法建立圆形搜索区域,匹配第二期的拟合植被圆心,搜索半径为1,半径阈值为0.3,共匹配到12对同名植被点云。

将拟合的圆心置于地面数据之中,以拟合圆心为球心、以2 m为半径建立球形区域。同名植被点云搜索到的地面点云中,符合点云数量差值为50、点云包围盒为0.2的即为同名特征区域,共找到8对同名地面特征区域。

2.4 变形分析

对从点云中提取的同名特征区域采用ICP算法进行变形分析。用配准后第一期同名地面特征区域C1′的重心坐标减去配准前的第一期同名地面特征区域C1的重心坐标得到地表移动值。如表1所示,使用点云的特征区域求取了山地边坡局部位移,包括下沉和水平移动信息,在此基础上绘制了水平移动矢量图,如图11所示。

图11 边坡水平位移矢量图Fig.11 Vector diagram of horizontal displacement of slope

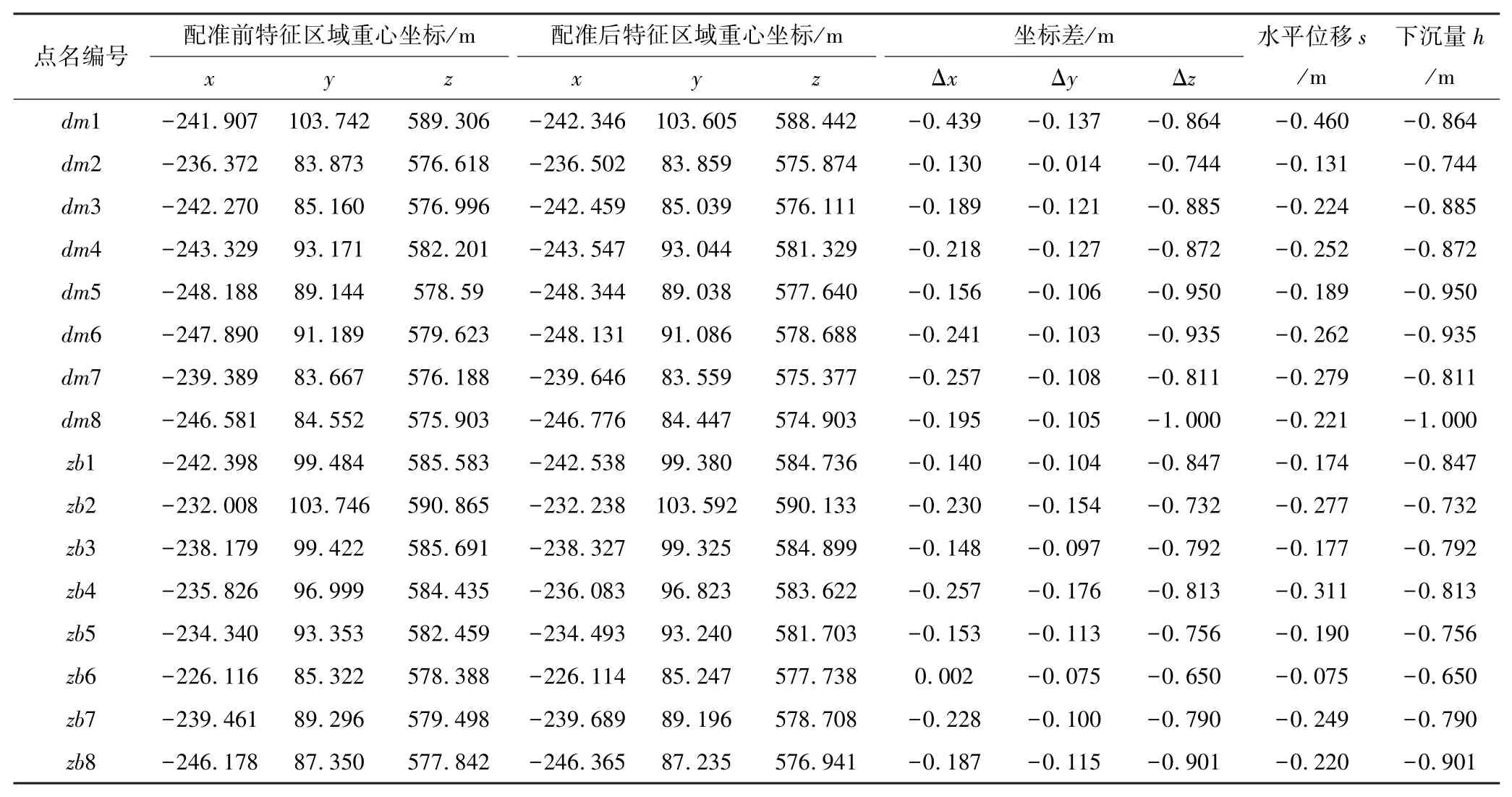
表1 特征区域重心点坐标配准前后变化值Table 1 Variation values of barycentric point coordinates before and after registration in feature region

由表1和图11可知:水平位移最大值0.46 m位于dm1点,最小值0.075 m位于zb6点,水平位移矢量方向指向西南方向。西南方向为监测对象的下坡方向,也是采空区所在方向,求取结果符合矿区开采沉陷规律。

利用表1中16个点的下沉值生成了地表下沉等值线图,如图12所示。由表1和图12可知:地表最大下沉值-1 m位于dm8点,地表最小下沉值-0.65 m位于zb6点;西侧地表下沉量多,东侧地表下沉量少,该结果与西侧距离采空区较近、东侧距离采空区较远有密切关系,监测到的下沉等值线符合开采沉陷规律。

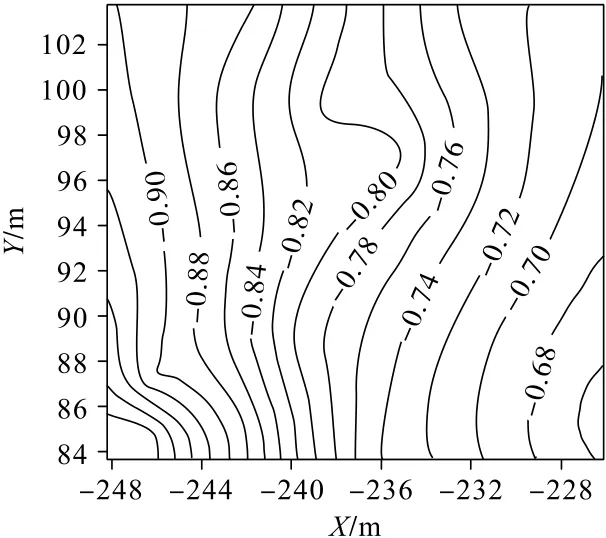
图12 地表下沉等值线图(单位:m)Fig.12 Contour of surface subsidence

为了分析FRICP算法计算变形的精度,采用人工精确判读方法进行对比,以16个重心点中的8个地面特征区域的重心点为参考,用Cloudcompare软件在两期原始点云中手工选出对应点云同名特征区域,使用该软件附带的ICP算法进行第一期和第二期同名点云特征区域配准,用配准后的第一期点云区域的重心减去原始的第一期点云特征区域重心,求出重心的差值。将其与FRICP算法计算的重心变形值进行了对比,结果见表2。

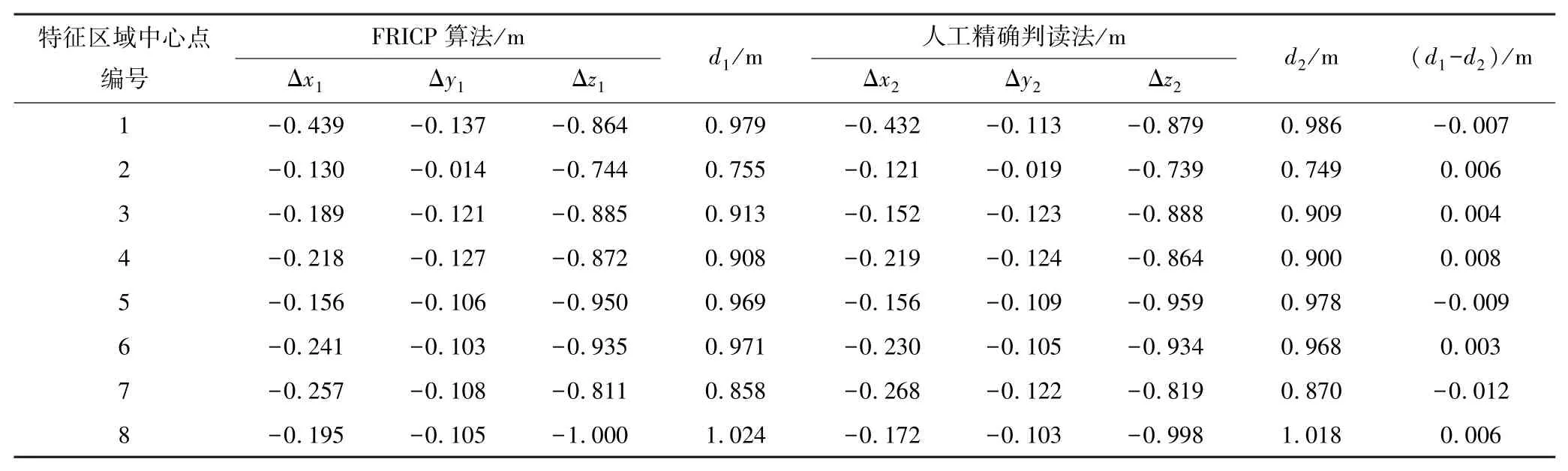
表2 FRICP算法与人工精确判读法精度对比Table 2 Comparison between the precise of FRICP algorithm and manual accurate interpretation method

由表2可知:FRICP算法自动计算和人工精确判读的地表位移值最大偏差为12 mm,最小偏差为3 mm,三维坐标位移中误差为7.882 mm,X方向中误差为14.966 mm,Y方向中误差为10.862 mm,Z方向中误差为7.818 mm。由此可见:FRICP算法对于地表移动值的计算精度接近固定测点的监测水平,对于分析煤矿地表变形有一定的实用价值。

3 结 论

(1)针对变形监测工作中三维激光扫描技术存在的多期测量无法直接获得同名点的不足,提出了特征区域概念,并建立了特征区域最近点迭代地表移动分析算法(FRICP)。该算法通过特征区域自动提取、同名匹配、ICP转换等步骤,实现了地表移动量计算。试验表明:该方法对于地表移动的监测精度能达到定点测量的技术水平。

(2)FRICP算法扩展了传统ICP算法的应用场景,突破了三维激光扫描技术应用于变形监测领域的技术瓶颈,具有一定的理论意义,在山区开采引起的地表移动监测等方面有较好的应用前景。

(3)本研究算法的较好应用场景是被监测范围内有明显的特征区域。在地表平坦、起伏不大且标志物较少的工况下,不明显特征区域的提取算法有待进一步研究。