炸药晶粒包覆结构对PBX 动态损伤影响的近场动力学模拟

黄亚飞，邓小良，柏劲松

（冲击波物理与爆轰物理重点实验室， 中国工程物理研究院流体物理研究所， 四川 绵阳 621999）

0 引 言

高 聚 物 粘 结 炸 药（Polymer Bonded Explosive，PBX）是固体高能炸药之一，在多种领域广泛使用，例如火箭推进剂和不同武器系统中的主炸药。它是通过一定的制作工艺使单质炸药晶粒包覆上高聚物粘接剂并通过压制而形成的颗粒复合材料。包覆材料的存在不仅能够提升炸药的综合性能，降低炸药摩擦感度和撞击感度［1-3］，而且能提升对炸药外界湿度、辐射等环境影响的抵抗力；从而能够有效避免炸药在制造，储存，运输和处理过程中由于外界刺激导致的意外点火，避免人员和财产的重大损失。因此，研究PBX 炸药的包覆结构对PBX 动态响应的影响对炸药设计和制造有着重大意义。

人们已经广泛研究了包覆结构对炸药性能的影响。徐庆兰［4］初步探讨了高聚物粘结炸药包覆过程及粘结机理。金韶华等［5］详细研究了高分子包覆的工艺方法、高分子种类、表面活性剂的应用，以及对于炸药性能的影响。黄亨建等［6］利用石蜡和芳香共聚物包覆RDX，对包覆RDX 颗粒制作的改性B 炸药开展了研究，在解决B 炸药性脆易裂问题上取得了一定的效果。张娟等［7］选用3 种材料对黑索今进行表面包覆并对包覆样品的撞击感度和摩擦感度分别作了测试，结果发现包覆后RDX 的撞击感度降低，摩擦刺激的反应没有明显变化。邢江涛等［8］通过分子动力学模拟研究了3 种高聚物对六硝基六氮杂异伍兹烷CL-20 的降感作用尤其是降低机械感度，研究表明丙烯酸酯橡胶（AR-71）对CL-20 的撞击感度有明显的改善。詹春红等［9-10］研究了主题炸药HMX 的颗粒特性与PBX 炸药包覆度以及PBX 成型性能的相互规律。随后还研究了氟橡胶F2311 特性粘度对高聚物粘结炸药成型及力学特性的影响。研究结果表明，1.95 dL·g-1的F2311 最适合作为HMX 基PBX 的粘接剂，用其制备的PBX 力学性能和成型性能得到明显改善。然而，这些研究主要集中在有关包覆结构的微观包覆机理以及对宏观层面性能变化的影响，目前关于不同包覆结构的PBX 在冲击加载下的动态响应，尤其是包覆结构如何影响动态损伤的起始和演化还缺乏深刻理解。

由于炸药的不透明性，从实验上很难实时观测到损伤在其内部的演化过程，所以数值模拟是炸药动态响应研究不可或缺的技术手段。例如，Xiao 等［11］在ABAQUS 中采用包含损伤的结构预测了PBX 在冲击载荷下的应力-应变关系。仿真结果与实验数据吻合良好。Wang 等［12］在冲击载荷作用下，对HMX 基PBX的热力学响应进行了介观尺度模拟，获得了等效应变和温度分布等信息。Bennett 等［13］简化了SCRAM 模型，建立了各向同性粘弹性统计裂纹力学模型（Visco-SCRAM）并将该模型嵌入到LS-DYNA 软件中，对受约束的PBX9501 爆炸冲击过程进行数值模拟，得到了样品表面的位移场分布，与实验测量相符。该模型已被广泛用于描述PBX 的动态损伤响应［11］。最近，有研究提出了一种新型的粘弹性微平面模型来模拟准脆性PBX 材料的行为［14］。该模型的特征在于它考虑了粘弹性行为以及损伤引起的各向异性。这些模拟结果可以帮助更好地理解炸药的力学损伤和点火行为。应该注意的是，基于网格的模拟方法不能有效地处理由裂纹和空隙等的演化引起的不连续性，因为其控制方程是空间微分表达式。为了处理裂纹演化等非连续性问题，通常需要特殊的技术来修改传统的计算模型［15］，这会耗费额外时间并且操作复杂［16］。

为有效处理裂纹等非连续性问题，国际上新近发展了非局域近场动力学理论（Peridynamics，PD）［17-18］。与FEM 模型相反，PD 中的控制方程是积分运算，而不是空间微分方程。因此，它避免了关于位移场的连续性的假设，从而允许自发的裂纹形成、扩展和相互作用。这种优势使PD 更加适合模拟损伤行为。PD 模拟已广泛用于研究各种材料（如玻璃，金属和复合材料等）的力学性能，在含能材料领域也有了初步应用。如Deng 等［19］基于PD 理论结合Voronoi 图对PBX建模，研究了含微观结构的PBX 计算模型冲击加载下的动态损伤响应，揭示了PBX 中穿晶损伤与沿晶损伤的竞争机制。Talamadupula 等［20］基于多物理耦合的PD 理论研究了PBX 中损伤的形成与演化及裂纹面摩擦对热点的影响。Huang 等［21］基于PD 理论，研究了带有约束的球壳炸药在低速撞击下的力学损伤响应，从应力波传播的角度分析了钢球壳材料参数是如何影响球壳炸药力学损伤行为的。上述基于PD 的模拟加深了人们对PBX 动态损伤响应的理解和认识。然而，PD 在含能材料领域的应用还比较少，尤其是考虑含能材料包覆结构等微介观结构方面的研究鲜有报道。

因此，本研究基于PD 理论，结合Voronoi 建模研究了冲击加载下炸药晶体包覆结构对PBX 动态损伤的影响，揭示了不同冲击速度和不同包覆结构下PBX的损伤行为和特点，详细分析了单层包覆结构和双层包覆结构对［21］包覆材料选择的敏感性，为PBX 中包覆结构的优化设计提供参考。

1 键基近场动力学理论

根据Silling［17］提出的近场动力学理论（Peridynamics，PD），通过考虑材料点x与可能无限数量的其他点x'之间的相互作用来分析物体的运动。因此，在材料点x与其他材料点之间可能存在无限数量的相互作用。我们假设材料点x和材料点之间的相互作用超出某个区域（近场域，半径为δ）而消失，该区域由H表示，如图1 所示。材料点x只能与它自己近场域内的材料点发生相互作用，这种相互作用称为键。PD 中的相互作用力由成对的力函数f表示，该函数表示材料点x与其近场域内的材料点x'形成的力矢量。因此，可以根据牛顿第二运动定律［18］给出材料点x的运动方程：

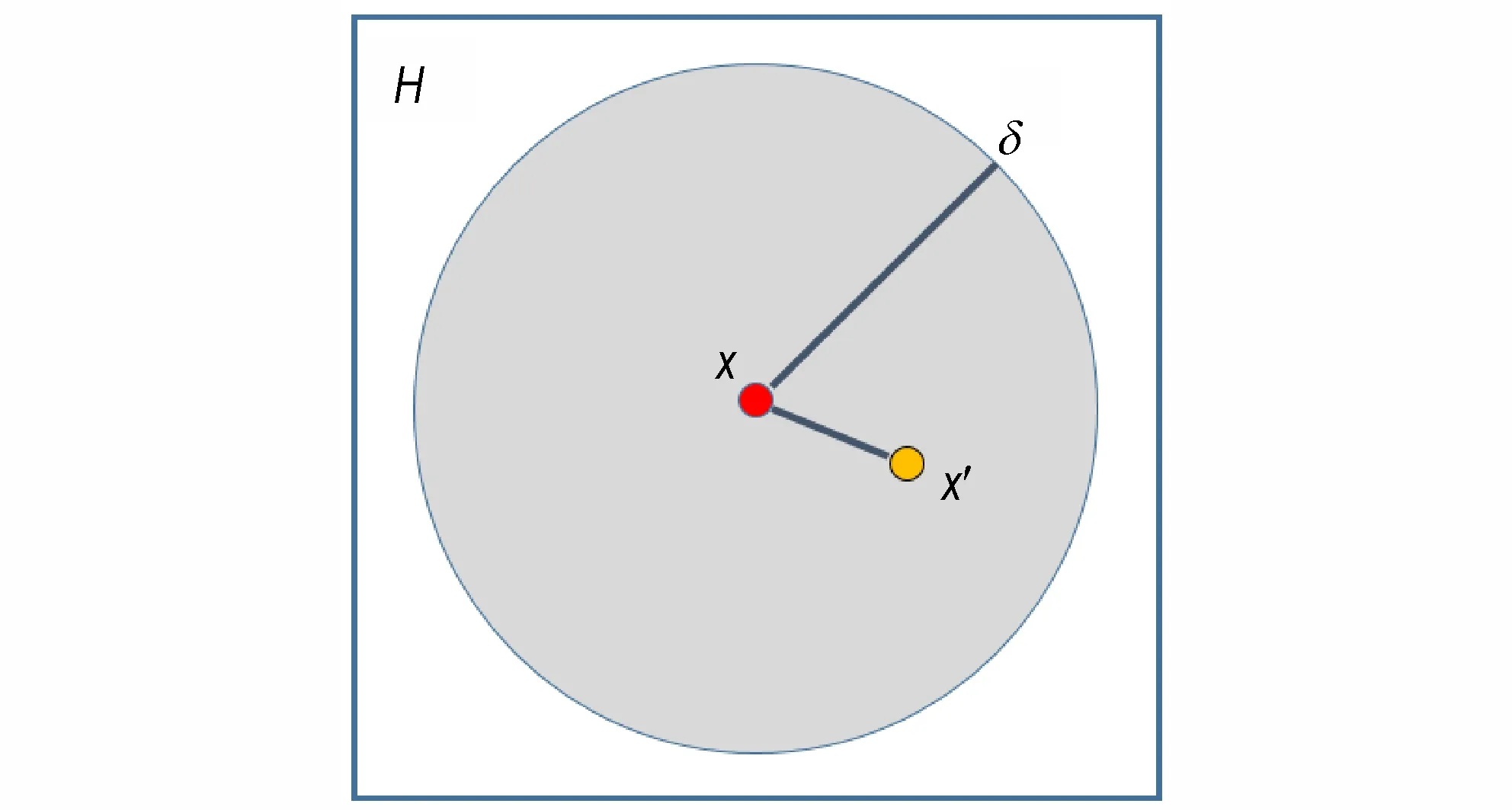
图1 材料点和近场域范围Fig.1 Material points and near field range

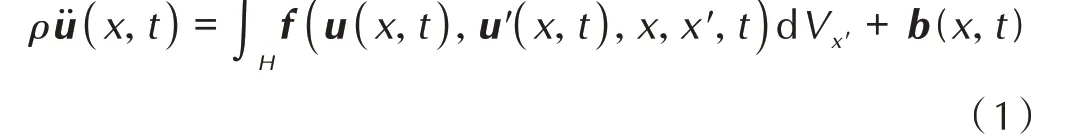
式中，ρ为材料点密度，kg·m-3；u为材料点位移，m；H为材料点近场域；V为材料点体积，m3；b为材料点体力密度，N·m-3。在三维模型中，近场域通常被视为以点x为中心半径为δ的球体。可以看出，当材料中出现不连续性时，PD 理论可以避免经典连续力学面临的数学上的奇异性。

在PD 理论中，材料点x的运动状态仅取决于其初始状态以及与近场域内所有材料点的相互作用。在经典的键基近场动力学理论中，微弹脆性模型（PBM）f可以用以下形式表示［18］，

式中，c代表微模量，kg·m-3；s为PD 键的相对伸长率；μ(t，ξ)为损伤函数。在PD 中，2 个材料点在参考构型中的相对位置矢量表示为ξ=x+x'，它们的相对位移表示为η=u'-u。结果，ξ+η表示变形构型中2 个材料点之间的当前相对位置。微模量是与经典连续体力学的材料常数相关的量，Silling 等通过经典连续理论的等效弹性和应变能密度推导出了微模量。它表示相同材料和相同形变情况下的应变能密度。三维情况下，c可以表示为杨氏模E和近场域半径的函数［18］：

在近场动力学中，通过引入损伤函数来描写材料的损伤行为［22］。当材料点x和材料点x'间的伸长率s超过其特定的临界值sc时，会引发材料点损伤。随后，运动方程中两点之间的相互作用将永久消除。损伤函数表示为［18］，

在模拟中，材料点在t时刻的损伤程度可以通过局部损伤进行量化，局部损伤定义为材料点的损伤键的数目与初始总PD 键数目的比值。某一点的局部损伤可以表示为［23-24］：

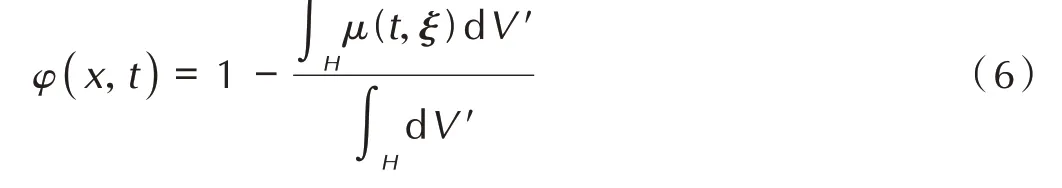
材料在t时刻的整体损伤程度可以通过损伤比进行量化，损伤比定义为材料中所有损伤键的数目与材料中初始的总PD 键数目的比值［25］。

模拟时计算域被离散为立方晶格，晶格常数为Δx，体积为Δx3。计算采用显式的Velocity-Verlet 算法［23，26-27］进行时间积分，以产生所有单个材料点的运动。时间步长Δt是满足稳定性条件［23，26-27］。

2 模型和边界条件

2.1 多晶模型

前期已对所用自研程序模拟结果进行了初步验证［19］。本研究构建了PBX 的近场动力学计算模型。矩 形样品模型沿x，y和z的尺寸分别为4.0，8.0 mm 和4.0 mm。计算过程中采用活塞方式进行冲击加载，冲击加载强度可以通过调节不同活塞速度得到。计算过程中，沿y方向的三层网格设为恒定速度的边界条件，其余为自由边界条件，模拟样品尺寸及加载方式如图2 所示。

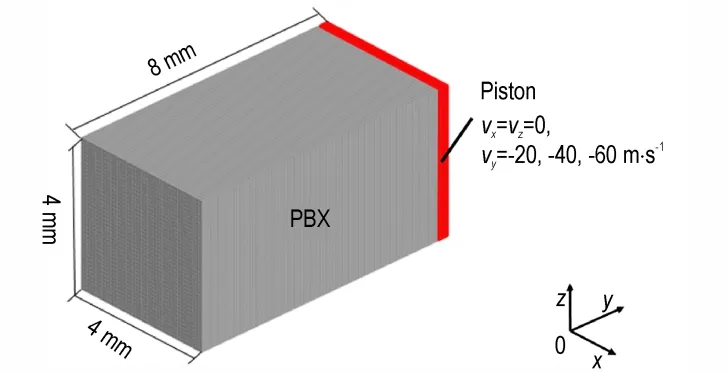
图2 计算模型的几何尺寸及其加载条件Fig.2 Dimensions of computational model and loading conditions

整个计算域被划分为三维矩形网格，网格尺寸为0.1 mm，材料点数目为128000。共有128 个HMX 晶粒，平均晶粒尺寸约为1 mm。为了描述PBX 结构中HMX 晶粒的包覆结构，该计算模型结合Voronoi 划分方法生成HMX 单层包覆结构和双层包覆结构，不同包覆结构的PD 模型如图3a，3b 所示。单个HMX 晶粒的包覆结构示意如图3c，3d 所示。模拟时间步Δt设置为10-9s，仿真持续时间为40 μs。

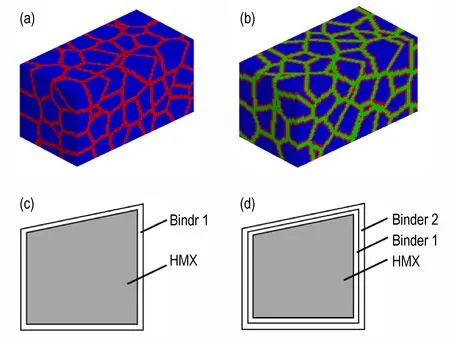
图3 HMX 晶粒的单层包覆结构和双层包覆结构：（a） HMX 晶粒的单层包覆结构；（b） HMX 晶粒的双层包覆结构；（c） 单个HMX 晶粒单层包覆结构示意图；（c） 单个HMX 晶粒双层包覆结构示意图Fig.3 Single-layer and double-layer coating structure： （a）HMX grains with single-layer coating structure； （b） HMX grains with double-layer coating structure； （c） Sketch of single-layer coating structure of single HMX grain； （d）Sketch of double-layer coating structure of single HMX grain

2.2 材料模型

对于PD 模拟来说，在2 个材料点之间相互作用模型对描述材料的真实行为至关重要。已发表的微弹性材料PD 模拟中，经常使用由Silling 和Askari 提出的微弹脆性模型［18］，如图4 所示。

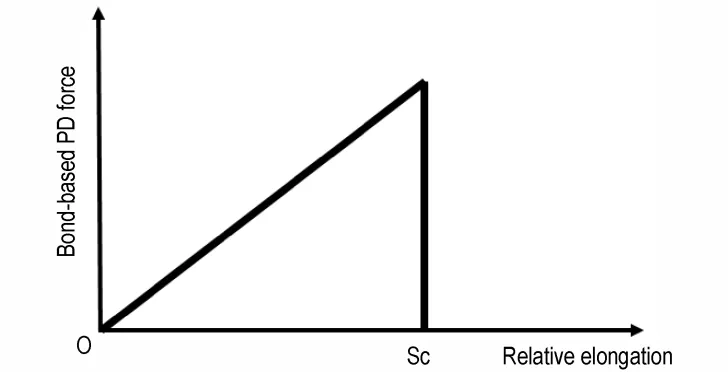
图4 微弹脆性模型［18］Fig.4 Prototype of micro-elastic brittle model［18］

需要说明的是，上述模型中的参数是在PD 键尺度上定义的，本研究所需参数通过拟合相应的实验数据来校准。因此，为了获得模拟的HMX 和包覆材料的应力应变数据，构建了如图5a 所示的PD 杆。尺寸为长32.0 mm，宽和厚22.0 mm。并且其边界区域沿纵向受到恒定速度载荷。左右边界区域的速度大小为0.1 mm·s-1，方向相反。近场域为δ=3.02 mm，杆由等间距网格Δx=1.0 mm离散。计算时间步长设置为Δt=1 ns，小于由方程（10）确定的200 ns 的临界时间步长。如图5b 所示，应力是根据样品中截面上的总PD 力除以该平面的面积来计算的。包覆材料粘接剂1 根据实验结果［18，28］校准，如图5b 所示。

经过材料参数的校准，得到参数列表如表1 所示。

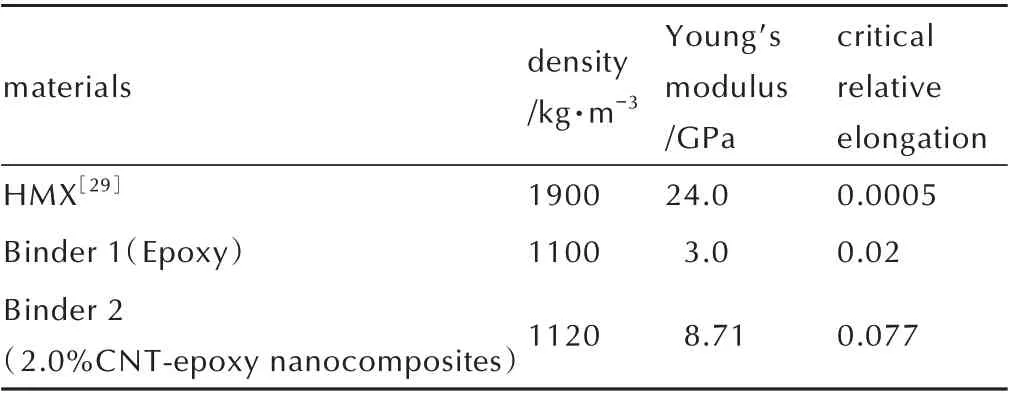
表1 材料参数Table 1 Material parameters used in the simulations

值得注意的是聚酯型聚氨酯、氟橡胶F2314 等具有复杂的非线弹性应力应变关系，微弹脆性模型无法很好描述他们的行为。本研究参考了文献中较为详细报道过断裂行为的2 种粘接剂：Epoxy 和2.0%NCT-epoxy nanocomposites，并结 合Yu 等［30］研究 中Epoxy 的断裂测试结果验证了参数以及程序的有效性。计算结果与文献中报道的加载-位移曲线符合很好（图5b）。

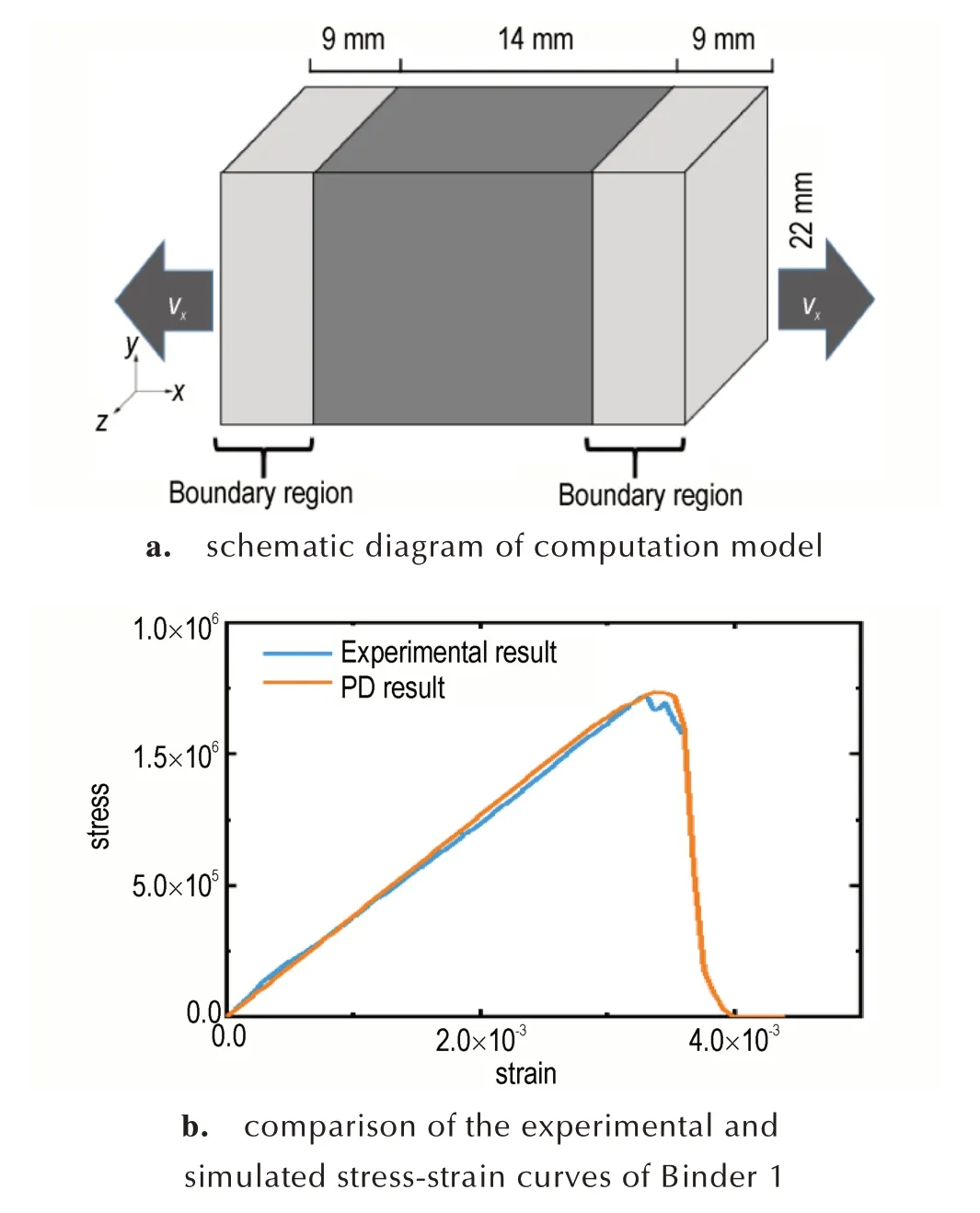
图5 根据实验结果校准Binder 1 的应力应变关系Fig.5 Stress-strain relationship

3 结果分析

3.1 单层包覆结构和双层包覆结构的HMX 损伤特点

为了对比采用单层包覆结构和双层包覆结构的HMX 晶粒的损伤特点，模拟设置了2 组算例：（a）样品中HMX 晶粒采用粘接剂1 进行单层包覆，单层粘接剂厚度为0.1 mm，沿厚度方向有1 层材料点。计算样品在加载速度v分别为20，40，60 m·s-1时的损伤情况；（b）样品中HMX 晶粒采用粘接剂1 进行双层包覆，每层粘接剂厚度为0.1 mm，每层粘接剂沿厚度方向有一层材料点。同样计算样品在加载速度v分别为20，40，60 m·s-1时的损伤情况。结果如图6 所示，样品中HMX 晶粒采用粘接剂1 单层包覆时，在20 m·s-1的加载速度下加载时间t为7.5 μs 时样品发生了轻微的损伤，且损伤主要发生在粘接剂附近，沿晶损伤较为明显，HMX 晶粒几乎无穿晶损伤发生（图6a）。在40 m·s-1的加载速度下加载时间t为3.75 μs 时样品发生了较为明显的损伤，且损伤主要发生在粘接剂附近，沿晶损伤明显，HMX 晶粒穿晶损伤明显（图6b）。在60 m·s-1的加载速度下加载时间t为2.5 μs 时样品发生了严重的损伤，沿晶损伤和HMX 晶粒穿晶伤都比较严重（图6c）。样品中HMX 晶粒采用粘接剂1 双层包覆时，在20 m·s-1的加载速度下加载时间t为7.5 μs 时样品发生了轻微的损伤，且损伤主要发生在粘接剂附近，沿晶损伤较为明显，HMX 晶粒几乎无穿晶损伤发生（图6d）。在40 m·s-1的加载速度下加载时间t为3.75 μs 时样品发生了较为明显的损伤，且损伤主要发生在粘接剂附近，沿晶损伤明显，HMX 晶粒穿晶损伤不明显（图6e）。在60 m·s-1的加载速度下加载时间t为2.5 μs 时样品发生了严重的损伤，沿晶损伤比较严重，HMX 晶粒穿晶损伤不严重（图6f）。图6 结果直观反映了采用包覆材料粘接剂1 双层包覆的HMX 比单层包覆的HMX 具有更好的抗损伤的能力。

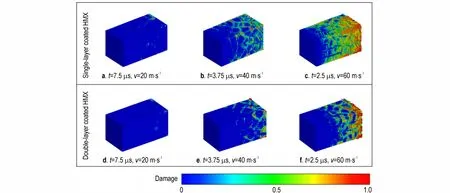
图6 相同加载位移下采用粘接剂1 单层包覆和双层包覆HMX 晶粒在3 种加载条件下的损伤分布Fig.6 Damage distribution of single-layer coating HMX grains and double-layer coating HMX grains with Binder 1 corresponding to the same loading displacement for three different loading conditions

另外，为了量化损伤程度和损伤分布特点，本研究给出了样品的损伤比［19，25］统计结果，经过分析得出了样品内部损伤的分布特点，如不同样品各加载条件下的沿晶损伤和穿晶损伤对比关系。这里用HMX 材料点与粘接剂材料点间键的损伤比来量化沿晶损伤程度，用HMX 材料点与HMX 材料点间键的损伤比来量化穿晶损伤程度［15］。结果如图7 所示，采用包覆材料粘接剂1 单层包覆的HMX 晶粒在3 种加载速度条件下均表现为穿晶损伤程度高于沿晶损伤，而采用包覆材料粘接剂1 双层包覆的HMX 晶粒在3 种加载速度条件下均表现为沿晶损伤程度高于穿晶损伤。说明对于粘接剂1，样品中HMX 晶粒采用双层包覆结构能够更好的被保护。

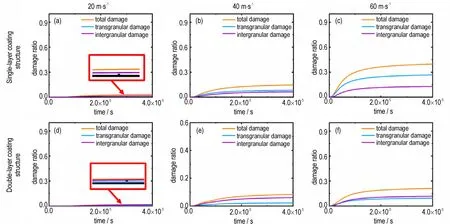
图7 不同包覆结构在不同加载条件下的损伤比Fig.7 Damage ratio under different loading conditions

另外，本研究对样品损伤稳定后的量化结果进行了分析。结果表明，样品的损伤程度随加载速度的增加而增大，且采用粘接剂1 的双层包覆结构，在3 种加载速度条件下HMX 的损伤程度均小于采用粘接剂1的单层包覆结构，如图8 所示。

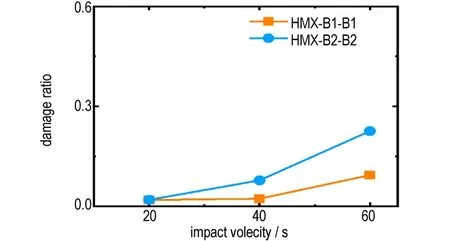
图8 采用粘接剂1 单层包覆和双层包覆的HMX 晶粒在3 种加载条件下的损伤对比Fig.8 Comparison of the two coating structures for three different loading conditions

由此，可以得出结论，采用粘接剂1 对样品中HMX 晶粒进行包覆，采用单层包覆结构时，撞击对HMX 晶粒的破坏较强；采用双层包覆结构时，撞击对HMX 晶粒的破坏较弱。表明双层包覆结构对HMX 的保护作用相比于单层包覆结构更强，不但能够降低了PBX 样品整体的损伤程度，还能将损伤分布由HMX 穿晶损伤转移到沿晶损伤，以此降低撞击对HMX 晶粒的破坏。研究不同单双层结构带来的影响，将对PBX的降感设计有一定参考价值。

3.2 包覆材料和包覆顺序对炸药晶体损伤的影响

为了探究包覆材料对包覆效果的影响，研究了2种包覆材料（粘接剂1 和粘接剂2）分别对单层包覆结构和双层包覆结构对HMX 晶粒保护效果的影响。

首先，对于采用单层包覆结构的样品，分别用粘接剂1 和粘接剂2 对PBX 样品中HMX 晶粒进行包覆，随后计算样品分别在20，40，60 m·s-1加载速度下的损伤行为。如图9 所示，采用单层包覆结构时，包覆材料的不同并没有引起PBX 损伤行为的明显变化。由此可见，采用单层包覆结构时，包覆材料的强度差异对HMX 晶粒的保护作用影响不明显。在双层包覆结构下，包覆材料的差异对HMX 晶粒的保护作用有明显的影响。从图9 中数据可以得出，采用粘接剂1 包覆时，相比于单层包覆而言，当加载速度分别为20，40 m·s-1和60 m·s-1时，双层包覆结构使HMX 晶粒的损伤分别降低了42.8%，87.2%和46.8%，明显降低了PBX 中HMX 晶 粒 的 损 伤。

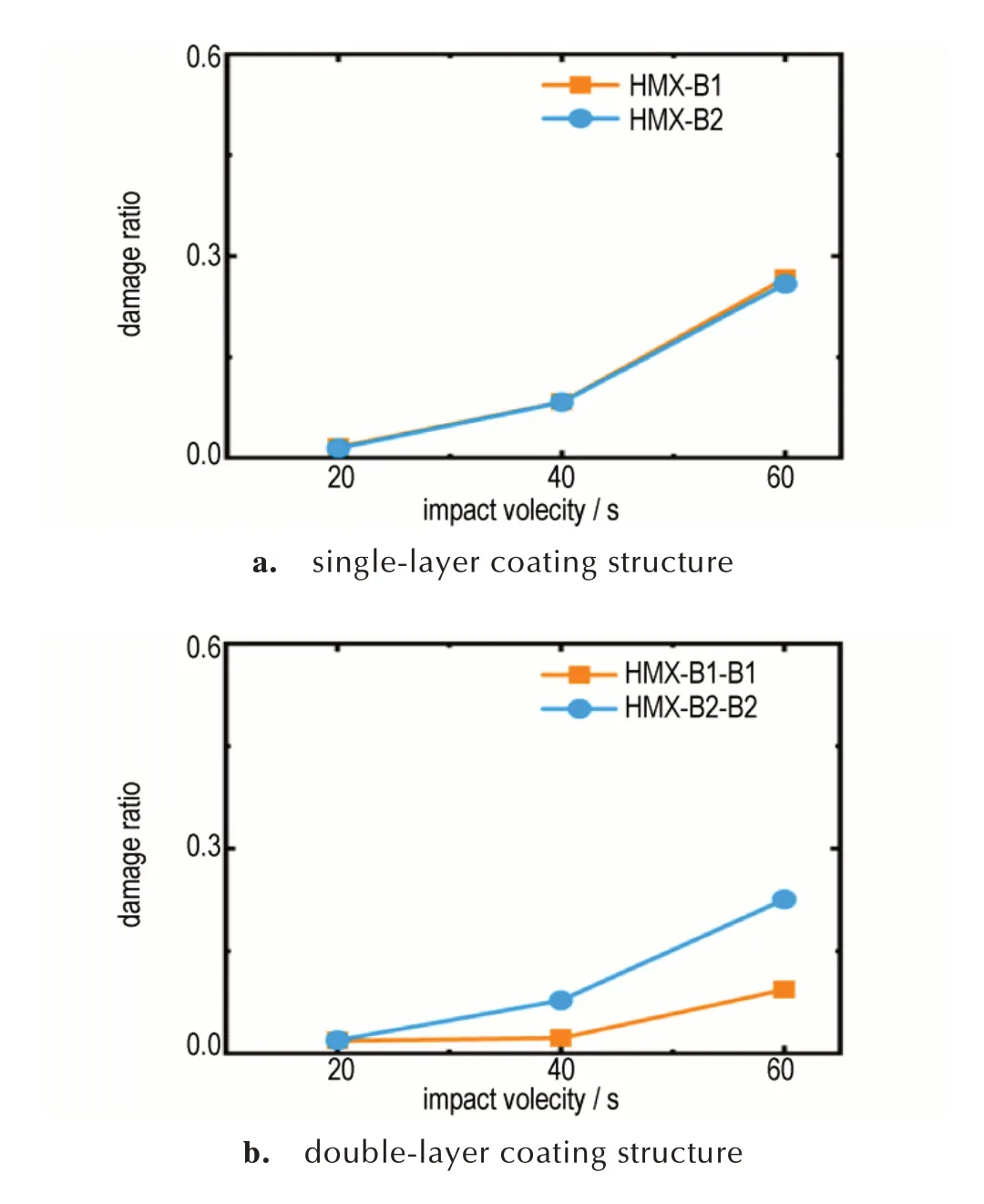
图9 单层包覆结构和双层包覆结构对包覆材料选择的敏感度Fig.9 Difference in the sensitivity to the two binders between single-layer coating structure and double-layer coating structure

另外我们还对双层包覆结构下的4 种情况（图10）进行了定量分析（加载条件为60 m·s-1），结果见图11。图11 可以看出，采用包覆顺序HMX-B2-B2时，PBX 的损伤程度最大，且穿晶损伤占比高于沿晶损伤占比，说明双层包覆结构下样品中的HMX 晶粒采用模量较高的粘接剂2 包覆时更容易损伤；采用包覆结构顺序分别为HMX-B2-B1，HMX-B1-B2，HMX-B1-B1时，PBX 的损伤程度逐渐降低，表明双层包覆结构下HMX 晶粒采用模量较低的粘接剂1 包覆抗损伤效果更好，且采用粘接剂1 直接包覆在HMX 晶粒表面更能起到保护效果。此外，损伤分布还按上述包覆结构顺序逐渐从HMX 晶粒的穿晶损伤转向沿晶损伤，且总损伤明显降低，尤其当采用HMX-B1-B1 包覆顺序时穿晶损伤占比低于沿晶损伤且总损伤最低。

图10 双层包覆结构中包覆材料的包覆顺序示意图［31-32］Fig.10 Schematic diagram of orders of coating materials in double-layer coating structure

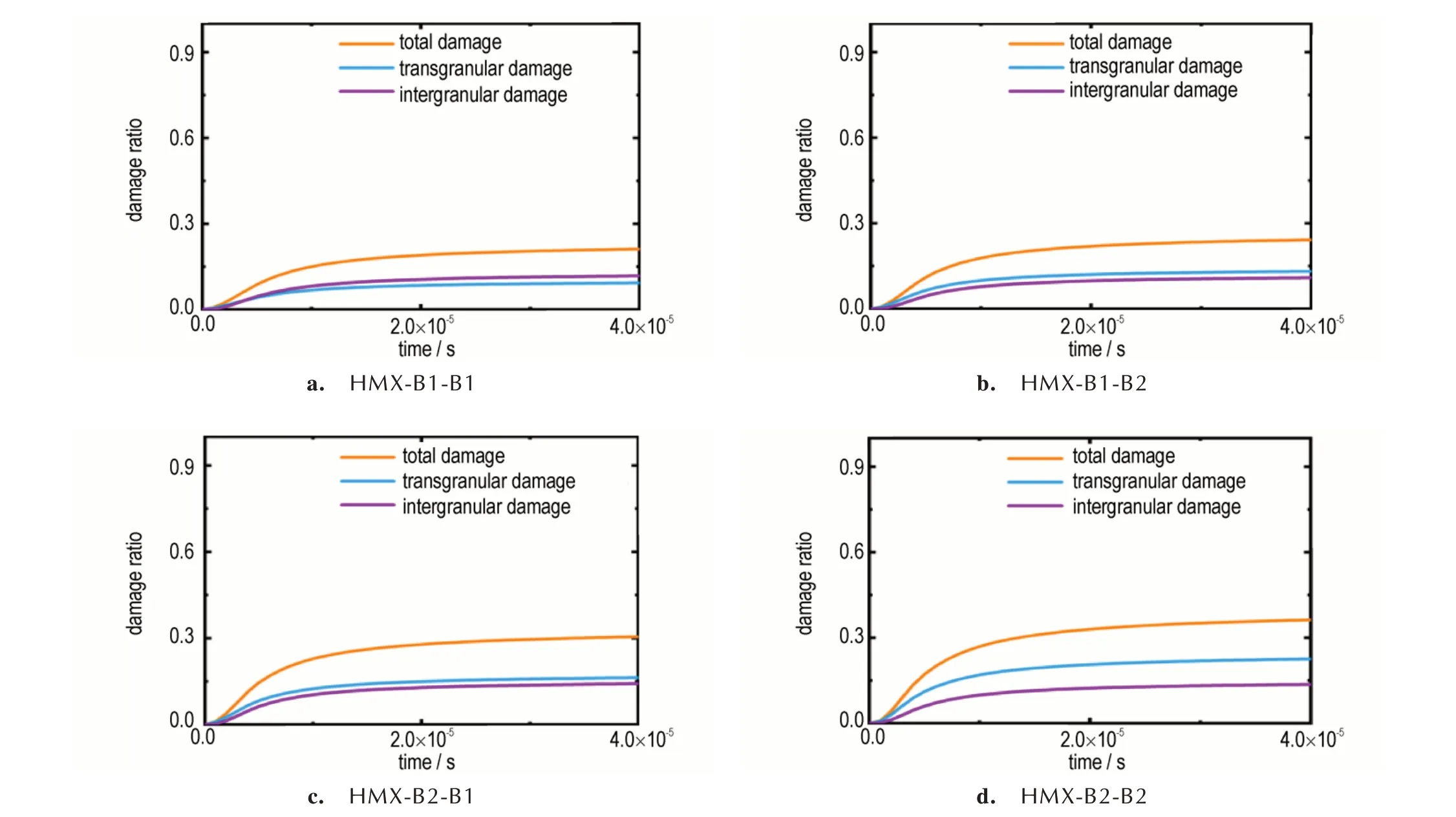
图11 4种包覆顺序下的损伤情况Fig.11 Damage of the four coating orders

由此得出结论，粘接剂1 对HMX 晶粒的保护作用优于粘接剂2，且粘接剂1 直接包覆在HMX 晶粒表面时对HMX 晶粒的保护作用更好。结合图12 对3 种加载条件下4 种包覆顺序对损伤影响的量化结果，4 种包覆顺序对HMX 晶粒的保护能力从高到低依次为：

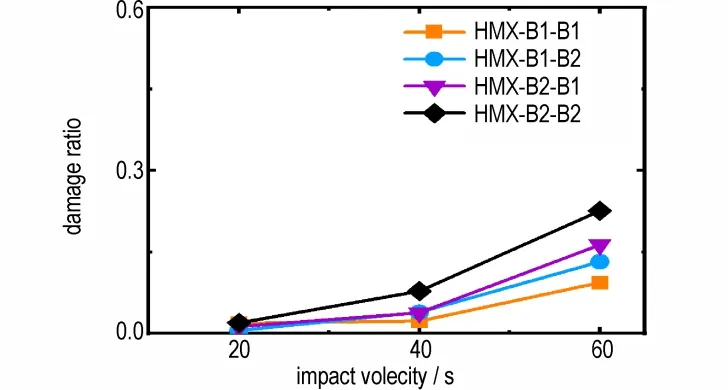
图12 4 种包覆顺序对损伤的影响Fig.12 Effects of the four coating orders on damage

HMX-B1-B1＞HMX-B1-B2＞HMX-B2-B1＞HMX-B2-B2。这对特定的PBX 设计，尤其是需要多种材料包覆HMX晶粒以满足特定需求的PBX 有一定参考价值。

3.3 不同包覆结构下的应力状态

模拟过程中材料点经历高应力状态是导致其损伤的直接因素，因此本研究对比分析了不同包覆结构在同种加载条件下相同时刻的应力状态对比情况并对材料点应力状态由低到高进行了量化对比，对不同的包覆结构是如何影响PBX 样品中HMX 晶粒损伤有了更加深刻的认识。

首先，对于HMX 晶粒采用粘接剂1 进行单层包覆和双层包覆的PBX 样品，在相同的加载条件下（v=60 m·s-1），图13 展示两者在相同时刻下的应力状态。图13 的结果显示，采用粘接剂1 双层包覆的HMX 晶粒中应力明显小于相同加载条件下相同时刻采用粘接剂1 单层包覆的HMX 晶粒。即采用粘接剂1 对HMX 晶粒的双层包覆结构通过降低HMX 晶粒经受的应力来起到保护更强的保护作用。

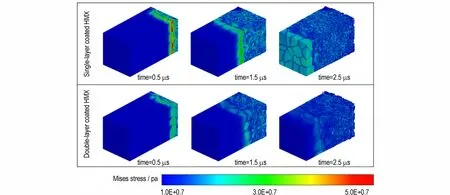
图13 采用粘接剂1 的2 种包覆结构在3 种加载条件下HMX 晶粒的应力状态对比Fig.13 Comparison of HMX stress state of the two coating structures with Binder 1 for three different loading conditions

同样，双层包覆结构下，粘接剂对HMX 晶粒的保护作用也体现在对HMX 经受应力的减弱。同时，本研究统计了不同包覆结构顺序HMX-B1-B1，HMX-B1-B2，HMX-B2-B1，HMX-B2-B2 在加载条件为60 m·s-1，模拟时间为1.5 μs 时HMX 材料点在不同应力区间（106～107Pa）的量化结果，如图14a 所示。结果表明，对HMX 晶粒保护作用较好的包覆结构（HMX-B1-B1），其较高应力状态材料点与总材料点的比例较低，相反，对HMX 晶粒保护作用较差的包覆结构（HMX-B2-B2），其较高应力状态材料点与总材料点的比例较高。此外，图14b 展示了不同包覆结构下的应力平均值，HMX-B1-B1，HMX-B1-B2，HMX-B2-B1，HMX-B2-B2 4 种不同包覆结构所对应的平均值分别为3.89，4.17，4.26，4.66 MPa，可以看出，较好的包覆结构也对应较低的平均应力。由于较高的应力状态通常导致较严重的损伤行为，因此应力分布结果与图12所得到的损伤分布一致，并从应力分布角度解释了包覆结构能对损伤状态的影响。

图14 1.5 μs 时刻加载条件v 为60 m·s-1时，不同包覆顺序下各应力范围HMX 材料点概率统计Fig.14 （a） Stress distribution of HMX material points for different coating orders at the speed of 60 m·s-1 and the time of 1.5 μs， （b） Calculated average stress （MPa） for different coating orders

4 结 论

本研究通过构建含单层包覆结构和双层包覆结构的PBX 近场动力学计算模型，研究了不同撞击加载条件下含不同包覆结构的PBX 的动态响应过程，比较了单层包覆结构和双层包覆结构对HMX 晶粒的保护能力，分析了2 种包覆结构对包覆材料选择的敏感性，以及双层包覆结构下包覆顺序对HMX 晶粒保护能力的影响，并从应力分布角度揭示了不同包覆结构对HMX晶粒损伤影响的机制。主要结论如下：

（1）相比单层包覆而言，双层包覆能够明显提高包覆材料对HMX 晶粒的保护作用。

（2）对HMX 晶粒单层包覆时，损伤主要发生在HMX 晶粒内，损伤模式主要表现为穿晶损伤。采用双层包覆时，损伤模式转变为沿晶损伤，HMX 晶粒得到更好保护，整体损伤得到了有效的降低。

（3）双层包覆结构下，粘接剂1 对HMX 晶粒的保护作用优于粘接剂2，且粘接剂1直接包覆在HMX 晶粒表面时对HMX 晶粒的保护作用更好。总体而言，4 种包覆顺序对HMX 晶粒的保护能力由高到低的顺序为：

HMX-B1-B1＞HMX-B1-B2＞HMX-B2-B1＞HMX-B2-B2。

（4）基于PD 模拟结果的应力分析表明，不同包覆结构影响HMX 晶粒内应力分布。性能较好的包覆结构能有效降低HMX 晶粒内较高的应力状态，从而降低外部加载下HMX 晶粒的损伤程度。

为PBX 炸药制备过程中包覆结构和包覆材料的选择以及双层包覆结构下包覆顺序的选择方面提供了有价值的参考。另一方面，该研究也体现了近场动力学理论在炸药领域中的应用潜在价值。