小型风电行星齿轮的结构设计及动力学分析

汲柏良，杜昱成，秦清海

(曲阜师范大学工学院，山东 日照 276800)

风电作为绿色清洁能源，是全球实现低碳、可持续发展的有效途径之一。我国的低风速区域分布广，占总面积的近7成[1]。近年来，国内低风速区的风电装机量迅速增加，进一步开发低风速区风能资源已经成为风电行业的共识。

风电机组按照风力机与发电机的传动链划分，可分为直驱、半直驱以及双馈3种类型[2]。半直驱方案采用“齿轮箱-永磁发电机-变频器”的技术路线，吸纳了直驱型与双馈型的长处，既在一定程度上避免了双馈型使用多级增速齿轮箱导致的故障率高的问题，又通过提高发电机输入转速相对降低了发电机的体积、重量及制造成本，半直驱渐渐成为兼顾生产制造成本与发电效益的最优解。

齿轮箱是一种工作于高空、低速环境下，受不规律风载提高发电机转速的机械传动装置。齿轮箱故障会造成风电机组停机，降低供电可靠性，对风电行星齿轮传动系统进行动力学分析具有重要的现实意义。Kahraman最早求解了包含齿侧间隙、齿形误差和时变啮合刚度等因素的数学模型表达形式[3]，建立了行星齿轮纯扭转动力学模型并求解分析[4]。文献[5-6]中推导了行星齿轮的平移-扭转动力学模型，文献[6]考虑了齿根裂纹对行星齿轮的影响，并对其进行了分析。文献[7]以人字齿行星齿轮为研究对象，推导了动力学微分方程模型，将受啮合相位影响的时变啮合刚度考虑其中，并分析受不均匀载荷影响时的变化规律。齿轮的啮合运动中，啮合的齿对数及啮合的位置随时间发生变化，因而齿轮的啮合刚度具备时变特征[8]。

本文主要研究低风速半直驱风电行星齿轮箱。首先对满足10 kW半直驱风力发电机运行条件下单级行星齿轮的各主要构件进行参数匹配与结构设计，而后基于经典力学定律，计入时变啮合刚度与综合啮合误差的影响，通过集中参数模型推导行星齿轮的平移-扭转时变非线性动力学微分方程组，最后通过四阶Runge-Kutta法对动力学微分方程组进行求解分析。

1 行星齿轮结构设计

半直驱风电机组如图1所示，主要包含三部分：第一部分为风力机，是风能捕获装置；第二部分为风电齿轮箱，是增速装置；第三部分为永磁同步发电机，是机电能量转换装置。

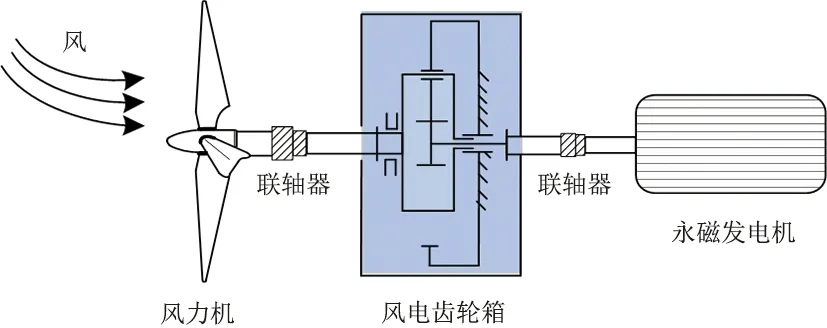
图1 半直驱风电机组

该风电机组主要运行于低风速工况下，输入转速低，转矩大。2Z-X型直行星齿轮结构简单、承载力强、效率高，因此将2Z-X型直行星齿轮作为风电齿轮箱的增速机构。行星齿轮所需的性能要求如表1所示。

表1 风电行星齿轮性能要求

(1)

式中：Kd为算式系数，取值为768；T1为啮合齿轮副中小齿轮的名义转矩；KA为使用系数，与随机载荷有关；KH∑为综合系数；KHP为载荷分布系数，与接触强度有关；φd为小齿轮齿宽系数；σHlim为接触强度下齿轮的接触疲劳极限；u为齿数比，“+”表示外啮合，“-”表示内啮合。

(2)

式中：Km为算式系数，取值为12.1；KFΣ为综合系数；KFP为载荷分布系数，与弯曲强度有关；YFa1为小齿轮齿形系数；z1为齿轮副中小齿轮齿数；σFlim为弯曲强度下齿轮的接触疲劳极限。

选取适当的参数分别代入式(1)与式(2)中计算可得：m1=4.33；m2=4.55。根据国标(GB/T 1357—2008)选定模数为5 mm。经计算，风电行星齿轮的系统参数如表2所示。

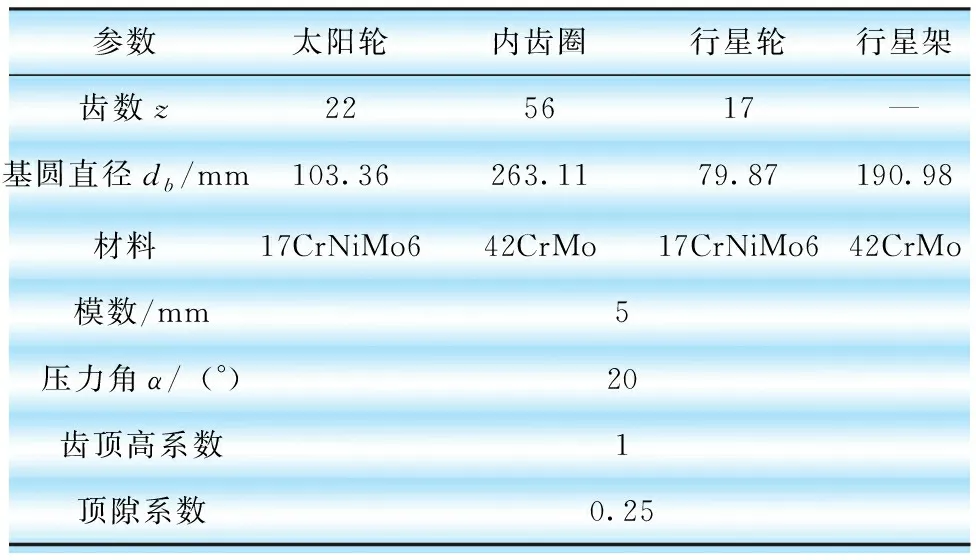
表2 风电行星齿轮系统参数

2 行星齿轮动力学模型

2.1 动力学建模

该风电行星齿轮传动系统中，内齿圈保持静止，扭矩由行星架侧输入轴输入，通过带动行星轮由太阳轮侧输出轴输出。

为简化分析，在建立平移-扭转耦合模型时忽略输入轴与输出轴对行星齿轮的影响；另行星齿轮为直齿轮，没有轴向力的参与，不计行星齿轮的轴向振动；3个行星齿轮的参数完全一致，并且是均载的；不计齿侧间隙以及摩擦对行星齿轮动态响应的作用；动力学模型中的阻尼都假定为线性阻尼。

基于上述假设，建立行星齿轮的平移-扭转耦合动力学模型如图2所示。图中有3个坐标系：坐标系OXY是静止坐标系；Oxy是旋转坐标系，其原点固定，两坐标轴与行星架同向等速旋转；onxnyn是以行星轮中心点为坐标原点，两坐标轴与坐标系Oxy两坐标轴分别平行且与行星轮等角速度旋转的动坐标系，n=1，2，3。

图2 平移-扭转耦合动力学模型

行星齿轮各构件包含3个自由度，2个平动x、y与1个扭转u。太阳轮、行星轮以及齿圈的直径分别取值为各自基圆的直径，行星架基圆的半径取值为太阳轮中心点与行星轮中心点间的距离。行星齿轮各构件经弹簧和阻尼器的并联结构相连接。ksp、csp分别表示太阳轮与行星轮间的啮合刚度与啮合阻尼；krp、crp分别表示齿圈与行星轮间的啮合刚度与啮合阻尼(p=1、2、3)。kl、cl(l=s、c、r、p)分别表示各个构件的支承刚度与支承阻尼；kcp、ccp表示行星架与行星轮间的支承刚度与支承阻尼。

以Δ表示弹性构件间的压缩形变量，太阳轮与行星轮间及齿圈与行星轮间的压缩形变量为

(3)

(4)

式中：αs、αr为太阳轮与行星轮及齿圈与行星轮间的啮合角(按照标准中心距安装时，啮合角等于分度圆压力角)；φi为各行星轮安装相位角；es(t)、er(t)为太阳轮与行星轮及齿圈与行星轮间的综合啮合误差。

第i个行星轮与太阳轮及第i个行星轮与齿圈间的啮合力为

(5)

式中：ksi为第i个行星轮与太阳轮间的啮合刚度；csi为第i个行星轮与太阳轮间的啮合阻尼；kri为第i个行星轮与齿圈间的啮合刚度；cri为第i个行星轮与齿圈间的啮合阻尼。

第i个行星轮与行星架间的形变量为

(6)

式中：αi为第i个行星轮的压力角。

行星轮与行星架间在x、y向上的支承力为

(7)

式中：kcpi为行星轮与行星架间的支承刚度；ccpi为行星轮与行星架间的支承阻尼。

各部件l在x、y及u向上的支承力为

(8)

式中：kl为部件l的支承刚度；cl为部件l的支承阻尼。

由此可得行星齿轮传动系统动力学微分方程组见式(9)—(12)。

(9)

(10)

(11)

(12)

式中：ms、mc、mr、mp、Js、Jc、Jr、Jp、Ts、Tc、Tr、Tp、Rbs、Rbc、Rbr、Rbp分别为太阳轮、行星架、齿圈与行星轮的质量、转动惯量、转矩以及基圆半径；ωc为行星架的转速。

2.2 参数分析

2.2.1 时变啮合刚度

太阳轮与行星轮间及齿圈与行星轮间，其啮合刚度随时间发生周期性变化，其主要原因如下。

a.啮合时齿轮的啮合对数发生改变。

b.轮齿啮合过程中，其啮合位置随时间发生改变。

行星齿轮各构件间的啮合刚度可使用与啮合频率有关的Fourier级数来等效，为简化计算，此处取其前三次谐波。

(13)

式中：ksiav、kriav分别为行星轮与太阳轮及行星轮与齿圈间的平均啮合刚度，可查阅GB/T 3480—1997计算得到；ksij、krij(j=1、2、3)为傅里叶系数；tsi、tri为太阳轮与各行星轮及齿圈与各行星轮啮合的时间差异；fm为啮合频率，可由式(14)计算得到[11]。

(14)

式中：fc为行星架转频；Zr为齿圈齿数；Zs为太阳轮齿数；fs为太阳轮转频。

2.2.2 综合啮合误差

综合啮合误差产生于齿轮生产制造的过程中，在齿轮啮合的过程中会造成冲击响应。在动力学模型中，可采用正弦函数的形式来近似表示。

(15)

式中：Es为齿轮副综合啮合误差的幅值；βs、βr为太阳轮与行星轮间及齿圈与行星轮间综合啮合误差的初相位。

2.2.3 各构件质量及转动惯量

行星齿轮中各构件质量可通过式(16)—(18)计算得到[14]。

(16)

式中：

dm=(da+df)/2

(17)

b=φdd1

(18)

式中：ρ为材料密度；d0为回转轴直径；B为齿宽；da为齿顶圆直径；df为齿根圆直径；φd为齿宽系数，d1为主动轮的分度圆直径。

各个构件的转动惯量为

(19)

3 计算结果分析

针对所选型设计的行星齿轮进行动力学分析，经计算各构件参数如表3所示。

表3 行星齿轮传动系统参数

基于前文所推导的行星齿轮动力学模型，代入以上参数降阶后采用四阶五级定步长Runge-Kutta法编程求解。

3.1 确定工况下的动态响应分析

在不考虑负载的情况下，设定行星齿轮的输入转速为20 r/min，输入转矩为4775 N·m。行星齿轮各构件的动态响应分别如图3(a)-(f)所示。

(a) 太阳轮x向振动位移

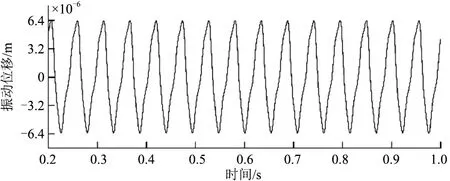
(b) 太阳轮y向振动位移

(c) 行星架x向振动位移

(d) 行星架y向振动位移

(e) 行星轮x向振动位移

(f) 行星轮y向振动位移图3 行星齿轮各构件动态响应

由图3(a)-(f)可知：各构件x向与y向的振动为非简谐周期振动。各构件x向振动位移的时程曲线关于y=0近似对称，太阳轮的x向振动位移幅值约为3.8 μm，行星架的x向振动位移幅值为0.96×10-3μm，行星轮的x向振动位移幅值为1.2×10-3μm。各构件y向振动位移中，太阳轮的y向振动位移幅值约为6.4 μm，行星架的y向振动位移幅值约为2.0×10-3μm，行星轮的y向振动位移幅值约为6.33 μm。

风电行星齿轮传动系统往往运行在低速重载的环境下，系统中各个构件的振动幅度均在“微米”的数量级，可满足要求。

3.2 输入转速的影响分析

风电行星齿轮的太阳轮通过输出轴与发电机相连，太阳轮的动态响应关系到发电机的工况，故在不考虑负载条件下，设定输入转矩为4775 N·m，分别计算输入转速为10 r/min，20 r/min及30 r/min时的动态响应，得到太阳轮扭转方向的振动位移时域如图4所示，去除太阳轮扭转方向振动位移的直流分量并分别进行频域分析如图5(a)-(c)所示。

图4 不同转速下太阳轮扭转位移时域

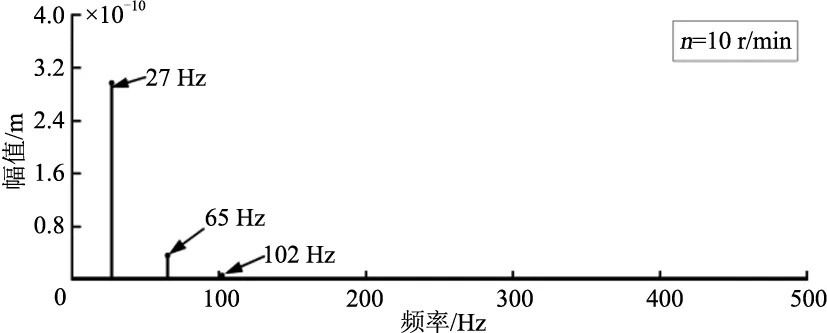
(a) n=10 r/min

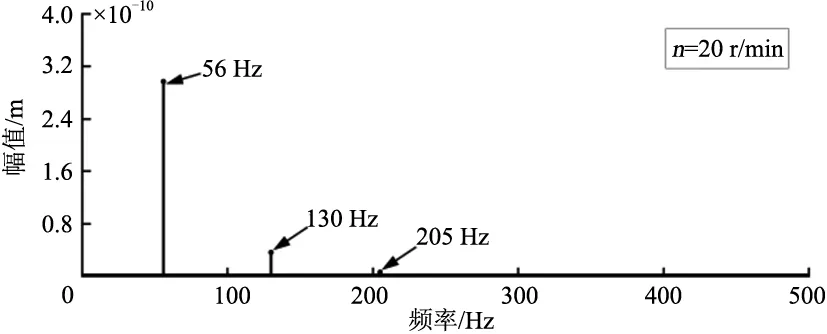
(b) n=20 r/min

(c) n=30 r/min图5 不同输入转速下太阳轮扭转位移频谱

由图4及图5(a)-(c)可知：在保持输入转矩为定值4775 N·m时，改变行星齿轮的输入转速，其扭转振动位移的峰值均为34.15 μm，由此可见定转矩下，输入转速的变化对太阳轮扭转位移幅值的影响非常小；行星齿轮中太阳轮扭转位移的频率分布与行星齿轮的啮合频率有关，主要为啮合频率及其倍频，并且与转速成线性关系。

3.3 输入转矩的影响分析

不考虑负载影响，设定输入转速为20 r/min，计算输入转矩分别为500 N·m、2000 N·m以及4775 N·m时太阳轮扭转位移的动态响应，得到太阳轮扭转方向的振动位移时域如图6所示，同样去除太阳轮扭转方向振动位移的直流分量并分别进行频域分析如图7(a)-(c)所示。

图6 不同转矩下太阳轮扭转位移时域

(a) T=500 N·m

(b) T=2000 N·m

(c) T=4775 N·m图7 不同输入转矩下太阳轮扭转位移频谱

由图6及图7(a)-(c)可知：在输入转速不变情况下，当行星齿轮的输入转矩分别为500 N·m、2000 N·m以及4775 N·m时，太阳轮的扭转位移幅值分别为3.57 μm、14.30 μm、34.15 μm，峰值分别为0.28 μm、1.13 μm、2.71 μm，因此太阳轮的扭转位移会随着输入转矩的增大而缓慢增大，扭转位移的数量级仍处于“微米”级别；输入转矩仅对太阳轮扭转位移的幅值产生正相关影响，与太阳轮扭转位移频率分布无关。

4 结语

a.风电行星齿轮在低速重载的工况下，太阳轮相比于齿圈与行星轮，其x向与y向振动位移相对较大，但其振动幅值仍维持在“微米”级。

b.在仅行星齿轮的输入转速发生变化的情况下，其扭转位移的振动幅值不会发生变化，扭转位移的频率分布主要为啮合频率的倍频，并且与转速成强线性关系。

c.在行星齿轮的输入转矩发生变化的情况下，其扭转位移的振动幅值随着输入转矩而增大，扭转位移的频率分布并未随转矩的变化而发生改变。