基于阻抗特性的次/超同步振荡风电场振荡源识别及切机策略

秦 爽，李忠憓，岳 涵，夏德明

(国家电网有限公司东北分部，辽宁 沈阳 110181)

近年来，我国能源结构发生了深刻变革。2020年底风电、光伏已成为国家电网有限公司第二、三大电源，预计2050年新能源发电量占比将达60%左右[1]。风电通过电力电子变流器并网的电源正显著改变着电力系统的动态行为，其激发出的振荡曾引发数百公里外的火电机组无序跳闸[2]。

传统的控制手段无法有效应对这类新型振荡。一方面，当前的阻尼控制技术侧重于解决特定场景下特定振荡模式的稳定问题，难以适用于多设备多控制环节强交互、频率多模态漂移且广域扩散的宽频带振荡场景[3-4]。另一方面，高比例电力电子电力系统高效精确建模及仿真技术面临着难以克服的等值难题和维数灾难问题[5-6]，控制算法计算难度大。实际电力系统中成千上万台风机经不同的变流器、风力机变压器、馈线和主变压器并入系统，并且风电场内配置有多种类型的动态无功补偿装置。而现有研究通常基于单一或有限个不同型号的变流器及场站无功补偿装置进行等值建模，因此得出的次同步振荡机理只能用作定性分析，提出的抑制措施在实际应用中也具有一定局限性[7-9]。

本文首先给出了振荡源的识别方法，分析了次/超同步振荡期间风电场的阻抗特性，然后提出了优先切除振荡源的高效切机策略。最后，以新疆哈密、景峡南及河北沽源风电场景的实例和仿真验证了所提策略的有效性及适应性[10-12]。

1 基于阻抗特性的次/超同步振荡风电场振荡源识别及切机策略

1.1 振荡源识别方法

由式(1)、式(2)可知，电网激励源频率发生变化时，感性元件感抗和容性元件容抗绝对值也会随之发生变化，且二者趋势相反。因此，将电网等效为有源RLC串联电路，一定存在频率f0，使得系统总电抗为零，如式(3)、式(4)所示。若此时电网总电阻接近零或为负值，且f0互补于火电机组轴系自然扭振频率，则会引发次同步振荡[13]，f0即为次同步振荡频率。

XL=2πfLt

(1)

(2)

XL(f0)+XC(f0)=0

(3)

(4)

式中：f为电网激励源频率；XL和XC为电网感性元件总感抗和容性元件总容抗；Lt和Ct为电网感性元件总电感和容性元件总电容。

根据以上分析，振荡源识别方法是：一般情况下，电网总电阻为正值，对于不含串补的电网，发生振荡的必要条件是有呈负电阻、容性的元件，即风电场阻抗角满足式(5)；同理，对于含串补的电网，发生振荡的必要条件是有呈负电阻、感性的元件，即风电场阻抗角满足式(6)。定义呈上述特性的风电场为振荡源。

180°≤φnc≤270°

(5)

90°≤φsc≤180°

(6)

式中：φnc为不含串补电网风电场振荡源阻抗角；φsc为含串补电网风电场振荡源阻抗角。

特殊的是当振荡源呈负电阻、容性时，除次同步振荡外，在额定频率为50 Hz的电网中，还会引发频率为100-f0超同步振荡[14]。

1.2 风机阻抗特性分析

由于风电群甚至单一风电机组建模较为复杂，本文参考文献[15]采用电路结构较为简单的文氏桥正弦波发生器来分析次/超同步振荡下风机阻抗特性，以证明振荡源识别方法的正确性。文氏桥正弦波发生器及其等值电路如图1所示。

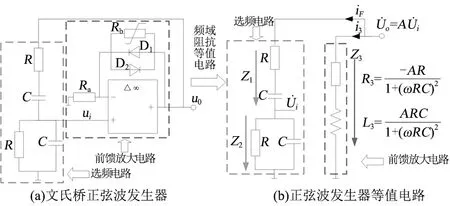
(a)文氏桥正弦波发生器(b)等值电路图1 文氏桥正弦波发生器及其等值电路

图1(a)所示的文氏桥正弦波发生器包含阻容式选频电路和前馈放大电路。其中，RC串联支路和RC并联支路串联构成选频电路，固定电阻Ra、可调电阻Rb、反向并联二极管D1和D2构成前馈放大电路。前馈放大电路放大倍数可由式(7)、式(8)求得。

(7)

(8)

式中：ui和uo分别为文氏桥正弦波发生器的输入电压和输出电压；Ra和Rb分别为前馈放大电路的固定电阻和可调电阻；A为前馈放大电路放大倍数。

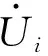
Z1(ω0)+Z2(ω0)=0

(9)

(10)

(11)

(12)

(13)

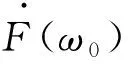
文氏桥电路的阻抗Z可由式(14)、式(15)求得。

(14)

Z=Z1+Z2+Z3=

(15)

式中：Z为文氏桥电路总阻抗。

文氏桥电路总阻抗Z的频率特性如图2所示，当Z的电抗部分为零时，若A<3，电路呈正阻性，不会启振；若A≥3，电阻接近零或为负值，呈现等幅或增幅振荡。

图2 文氏桥正弦波发生器阻抗Z频率特性

1.3 次/超同步振荡风电场切机策略

基于振荡源阻抗特性，提出以下次/超同步振荡风电场切机策略。

a.对于经串补送出的风电场，优先切除次同步阻抗角90°≤φsc≤180°范围内风电场进线；

b.对于未含串补的电网，优先切除次/超同步阻抗角180°≤φnc≤270°范围内风电场进线。

2 策略验证

2.1 直驱风机接入弱电网场景实例验证

新疆哈密地区风电群为直驱风机接入弱电网场景，总规模约3750 MW，直驱机型和双馈机型分别占比71%和29%。风机经35 kV或110 kV馈线接入220 kV风电汇集站，汇集站又经数十甚至上百公里线路接入500 kV三塘湖变电站，如图3所示。

图3 新疆哈密地区风电群汇入三塘湖变接线图

自2015年以来，哈密地区风电初具规模后，共计发生次/超同步振荡事件千余次。振荡分量甚至传导到300 km以外，引起3台660 MW火电机组因轴系扭振保护动作跳闸。对历史次/超同步振荡事故的相关风电场进行阻抗分析，直驱风机次/超同步振荡阻抗角180°～360°，呈容性，如表1所示。因此，阻抗特性为负电阻、容性的直驱风机是接入弱电网场景下激发振荡的源头。

表1 哈密地区次/超同步振荡频率及风机阻抗特性

2.2 双馈风机经串补线路接入电网场景仿真验证

河北沽源风电基地为双馈风机经串补线路接入电网场景，总容量约3420 MW，双馈、直驱、鼠笼机型占比分别为83%、15%、2%。基地24座风电场以辐射状接入500 kV沽源变电站，再通过2条同塔双回串补线路送出，补偿度分别为40%和45%，如图4所示。在PSCAD/EMTDC中搭建沽源风电基地并网模型，其中，华北主网和内蒙古电网用等效阻抗代替，以初始阻抗值±1%范围的变化模拟电网运行状态。

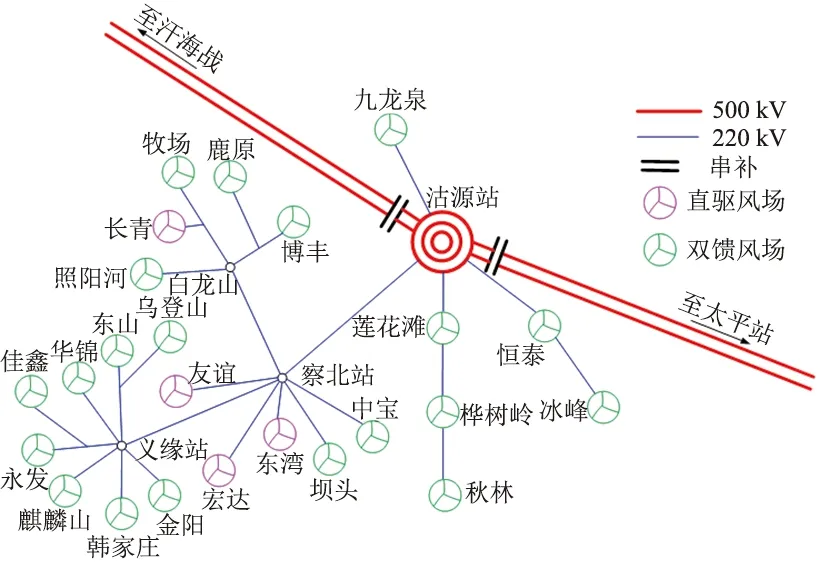
图4 沽源风电场结构

仿真通过风速调整诱发次同步振荡，t=1 s时，所有双馈风电场风速由7.0 m/s匀速下降；t=2 s时，风速降至5.4 m/s并保持；t=11 s时，所有风电场功率开始振荡。风速为5.4 m/s时,各风电场次同步频率阻抗如图5所示，由仿真结果可知，大部分双馈机型风电场呈负电阻性，直驱机型风电场则呈正电阻性。因此，阻抗特性为负电阻、感性的双馈风机为经串补线路接入电网场景下激发振荡的源头。

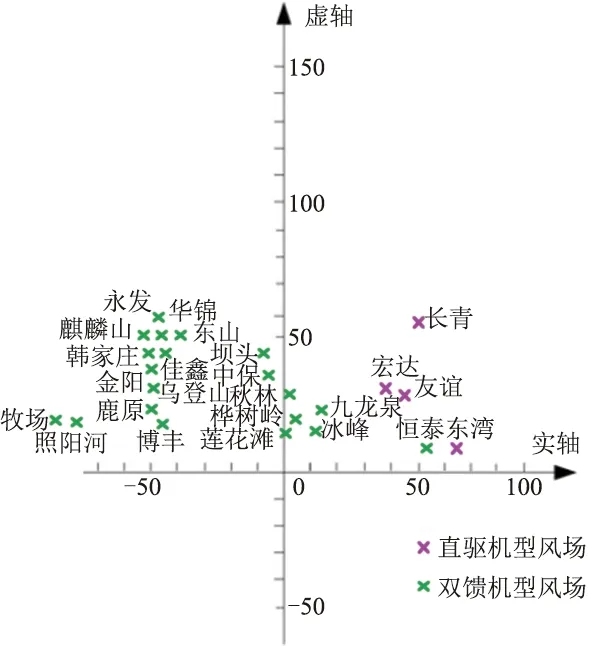
图5 风速为5.4 m/s时各风电场复阻抗图

按以下2种切除方式进行对比。

a.优先切除次同步阻抗角90°≤φsc≤180°范围内的风电场，依次切除2座双馈风电场后,振荡消失，如图6(a)所示。

(a) 优先切除90°≤φsc≤180°范围内风电场

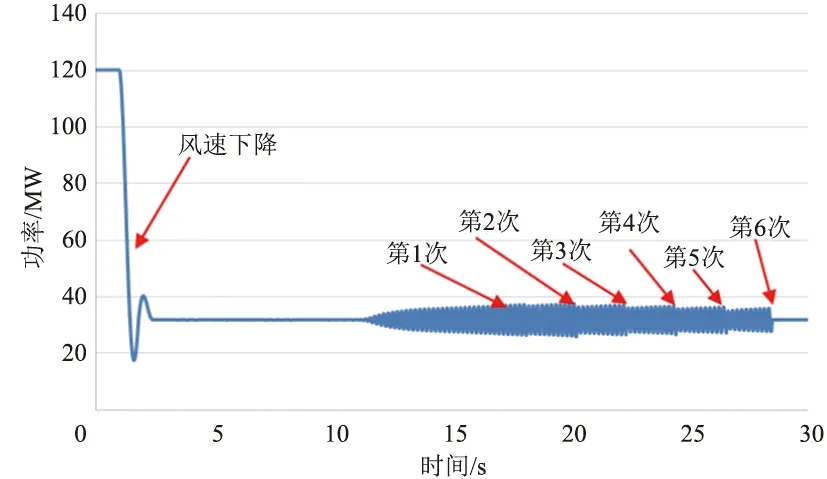
(b) 优先切除90°≤φsc≤180°范围外风电场图6 沽源风电基地某风电场仿真过程中功率曲线

b.优先切除次同步阻抗角90°≤φsc≤180°范围外的风电场，依次切除6座风电场后，振荡消失，如图6(b)所示。

以上实例及仿真结果证明了本文所提风电场振荡源识别及切机策略的正确性及高效性。

3 策略适应性分析

新疆景峡南汇集站为双馈风机加装静止无功发生器(static var generation，SVG)接入弱电网场景，景峡南1、2风电场各配置150台单机容量为2.0 MW的双馈型风电机组和3台容量为±24 Mvar的SVG，接线如图7所示。对2017年9月16日10：16：28：370的振荡数据进行频谱分析，明显存在64 Hz的振荡分量。由图8可知，风电场SVG谐波阻抗角波动范围为210°～240°；集电线谐波阻抗角波动范围为90°～105°；出线谐波阻抗角波动范围为230°～260°。

图7 景峡南风电汇集站接线图

(a)风电场SVG阻抗

(b)风电场集电线阻抗

(c) 风电场出线阻抗图8 风电场SVG、集电线及出线次同步阻抗实测值

风电场集电线阻抗呈负电阻、感性，不含串补的电网呈正电阻、感性，故二者不具备振荡条件，双馈风机非振荡源。而风电场SVG阻抗呈负电阻、容性，可引发振荡，故可判定SVG为振荡源。由图8(c)可知，风电场出线阻抗即风电场整体对外也呈负电阻、容性，因此本文策略同样适应于由双馈风电场SVG等其他源头引发的振荡。

4 结语

随着风电装机的迅猛增长，电力系统次/超同步振荡风险逐渐增大。而短期内又难以从理论分析和离线仿真方面取得突破性进展，以指导实际工程应用。鉴于此，本文提出了一种基于阻抗特性的次/超同步振荡风电场振荡源识别及切机策略，该策略可快速准确切除振荡源，高效化解电网振荡风险。同时该策略也适用于由风电场无功补偿装置、光伏电站等诸多源头引起的次/超同步振荡。使用该方法的次同步振荡监控装置已在东北电网得到初步应用。