燃煤电站碳捕集系统的分布式预测控制研究

伍 权， 杨晋宁， 王志勇， 徐 冬， 杨 阳， 唐子寒， 吴 啸

(1．国家能源集团新能源技术研究院有限公司，北京 102209；2．东南大学 大型发电装备安全运行与智能测控国家工程研究中心，南京 210096)

近年来，温室气体的持续排放导致了全球变暖、海平面上升等一系列环境问题，缓和全球气候变化已经成为国际社会的广泛共识[1]。在各类温室气体对气候变化的贡献中，CO2的贡献值在55%以上[2]。我国CO2排放主要来自化石燃料的燃烧，其中燃煤电站(Coal Fired Power Plant, CFPP)的 CO2排放量占总排放量的38.4%[3]。由于在未来的很长一段时间内，燃煤电站仍将占据我国电力供应的主力位置，研究燃煤电站CO2捕集对于实现我国“碳达峰”“碳中和”的战略目标具有极其重要的意义。

与此同时，随着可再生能源在电网中的接入比例不断上升，其间歇性和随机性特点严重影响了能源系统供能的稳定性和可靠性[4]。燃煤电站需要频繁深度参与调峰，以支撑可再生能源的消纳。相应地，碳捕集系统也需要灵活适应电站烟气质量流量的波动。因此，研究电站碳捕集系统的协同优化控制，是实现整体系统稳定、低碳和灵活运行的关键。

研究人员针对独立化学吸收燃烧后CO2捕集(Post-combustion Carbon Capture,PCC)系统的控制设计开展了研究。Lawal等[5]设计了基于比例积分(Proportional Integral, PI)控制的单变量反馈控制系统，分析了系统中补水控制的重要性；Posch等[6]提出一种比例控制系统，使贫液质量流量随烟气质量流量变化，以保持两者比值恒定，该设计可快速消除烟气质量流量变化的影响；Cormos等[7]开发了基于速率法的PCC全过程模型，并为其设计了模型预测控制器(Model Predictive Controller, MPC)。然而，上述研究未考虑PCC系统抽汽对发电机组的影响[8]，无法获得电站-碳捕集系统在发电和减排上的整体最优方案。Lawal等[9]建立了500 MW亚临界燃煤机组与化学吸收CO2捕集系统的耦合动态模型。该模型的动态仿真研究表明，火电机组的过渡过程时间要远远小于碳捕集系统，采用分散独立设计的PI反馈控制器无法考虑系统间的相互影响[10]，因此难以满足整体运行的要求。Wu等[11]在分析电站-碳捕集系统关键变量动态关联的基础上，设计了集中式MPC控制器，实现了电站-碳捕集系统的灵活运行。但由于集中式控制器涉及参数多、结构复杂，系统在线优化计算量较大，实时性较差。同时，由于系统局部故障将导致整个控制系统停运，控制器的可靠性较低。

分布式预测控制是在分散式控制的基础上，考虑系统间耦合关联和整体优化的新型复杂系统优化控制方法。该控制方法将大规模互联系统分解成若干个含耦合项的子系统，将优化问题解耦成若干个独立且耦合的子优化问题，独立设计的局部控制器间可通信和共享信息，其在缩小系统规模、提高求解效率的同时，各局部控制器相互协调运行，保证了控制性能的全局最优性[12]。分布式预测控制已在微电网系统[13]、多区域建筑供热[14]等能源领域得到较好应用。然而，尚未有研究将分布式预测方法应用于CFPP-PCC系统的协同控制中。

综上，笔者采用分布式预测控制，为CFPP和PCC系统分别设计局部预测控制器，并在控制器的预测模型和性能指标构造中引入关于另一控制器的状态信息项，实现局部控制器间的相互感知。进行在线优化求解时，局部控制器通过信息共享和迭代交互，对全局运行目标进行优化，实现了CFPP-PCC整体系统的稳定、低碳与灵活运行。

1 系统描述

1.1 CFPP-PCC系统结构

660 MW超临界CFPP耦合单乙醇胺(Monoethalnoamine, MEA)化学吸收PCC系统如图1所示。CFPP产生的烟气经脱硝、脱硫、除尘等预处理后被送入PCC系统的吸收塔底部，与从塔顶进入的吸收剂贫液逆向接触，烟气中的CO2被化学吸收。脱碳后的烟气从吸收塔顶部排入大气，富含CO2的溶液从吸收塔底部流出，经换热器后进入分离塔，在汽轮机中低压缸所抽取蒸汽的加热下，释放溶液中的CO2，进行溶剂再生。脱离后的CO2蒸汽从分离塔顶部进入凝汽器，并经压缩后被送入下游输送管道。再生的贫液经换热、冷却后被送入吸收塔循环工作[15]。

笔者将采用Liao等[16]基于gCCS仿真软件[17]搭建的660 MW超临界CFPP-PCC系统仿真模型。典型工况下CFPP-PCC系统主要变量的运行参数如表1所示。

1.2 CFPP-PCC系统动态特性

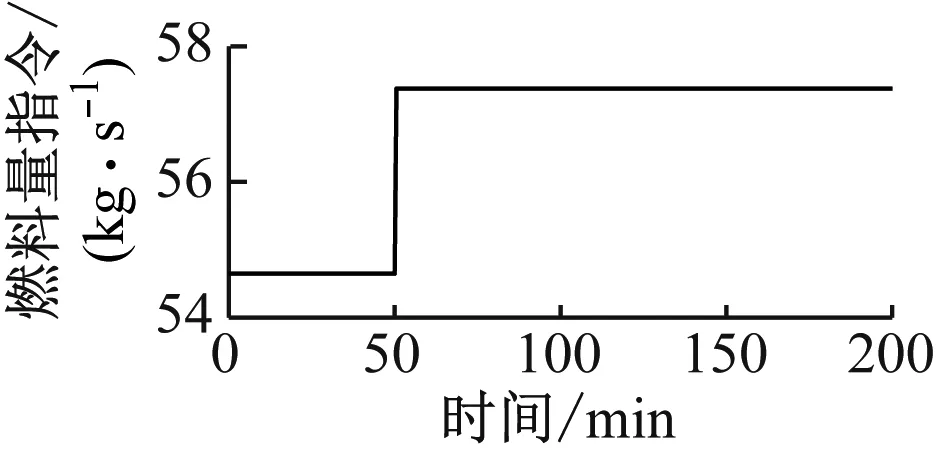
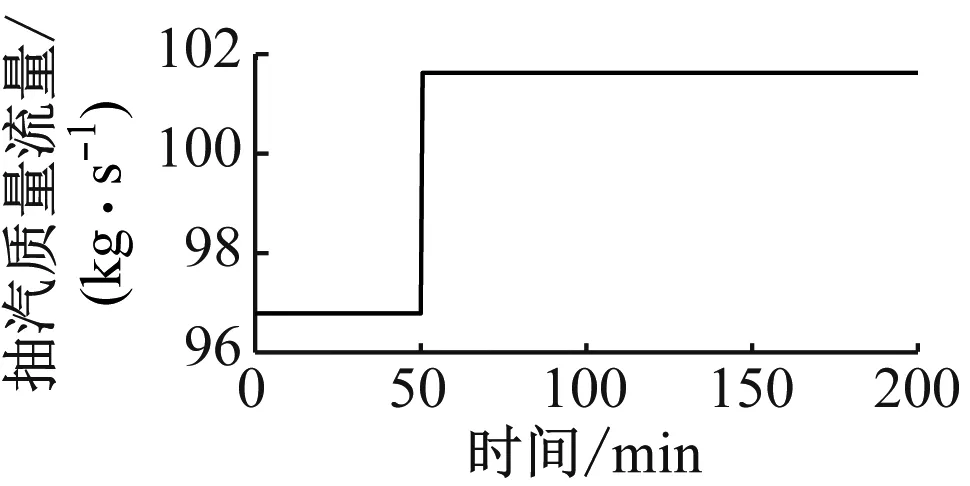
由图1可知，CFPP和PCC系统通过烟气和再沸器抽汽相互耦合，因此有必要深入了解2个系统间的动态相互作用，通过开环阶跃响应测试，分析2个系统的动态耦合特性。假设初始时刻CFPP-PCC系统处于表1所示的稳态工况点。在第20 min时，燃料质量流量和抽汽质量流量分别阶跃增加5%，CFPP-PCC系统中主要变量的动态响应如图2和图3所示。

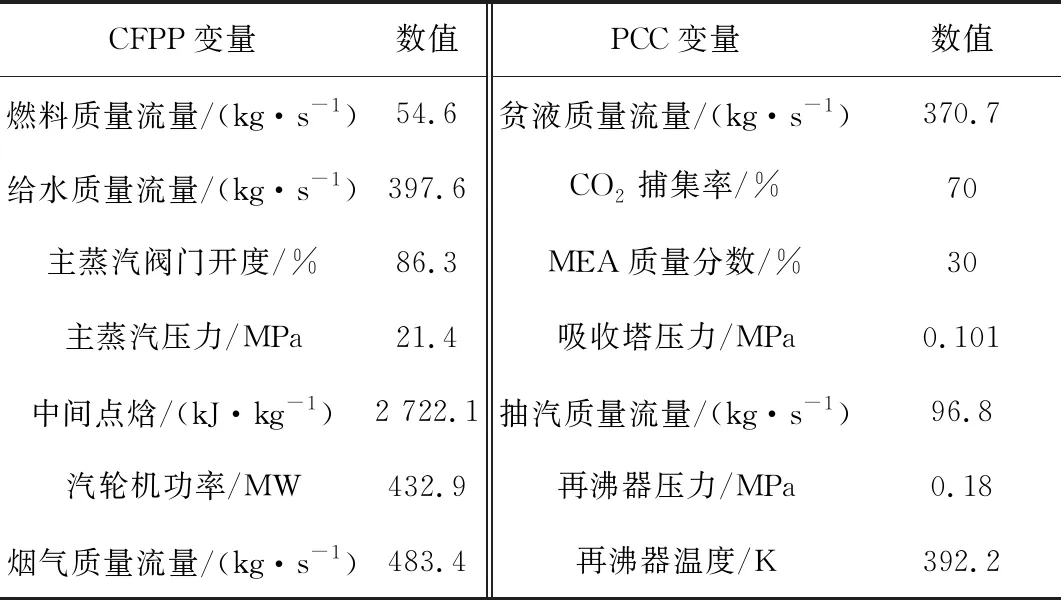
表1 典型工况下CFPP-PCC系统主要变量运行参数

图1 660 MW超临界CFPP-PCC系统流程图

由图2可知，增加燃料质量流量可以有效提升主蒸汽压力和汽轮机功率，因此可通过控制燃料质量流量来满足发电负荷的需求。同时，燃料质量流量变化会引起烟气质量流量的改变，从而影响下游的CO2捕集系统，导致CO2捕集率下降，而再沸器温度基本不变。由图3可知，通过改变抽汽质量流量可以快速调节汽轮机功率。同时，增大抽汽质量流量会使再沸器温度上升，从而降低贫液负荷，最终PCC系统的CO2捕集率得到提高。由于中间点焓和主蒸汽压力受抽汽质量流量变化的影响较小，因此图3中未展示其响应曲线。综合比较图2和图3可知， PCC系统相比于CFPP系统具有更强的惯性，同时二者具有很强的耦合作用，单独的分散控制方法难以实现CFPP-PCC系统的稳定、灵活运行。因此，笔者采用分布式MPC控制方法，设计合理的局部控制器，并通过控制器间的信息共享来考虑2个系统的相互耦合作用，实现电碳两侧控制效果的全局优化。

(a)

(a)

2 燃煤电站CO2捕集系统分布式预测控制

2.1 CFPP-PCC分布式预测控制算法

本文采用动态矩阵控制(Dynamic Matrix Control, DMC)算法实现CFPP和PCC系统的预测控制设计，该算法是一种基于被控对象阶跃响应的预测控制算法。根据文献[18]和文献[19]中的原理实现DMC算法的分布式求解。采用Liao等[16]搭建的660 MW超临界燃煤火电机组和燃烧后CO2捕集系统整体动态模型，得到CFPP-PCC系统各被控量对各控制量的阶跃响应，获取相应的阶跃响应系数。为了设计局部MPC控制器，对CFPP和PCC 2个系统建立多变量预测模型，以CFPP系统为例，建立如下预测模型：

ACPΔuPCC,M(k)

(1)

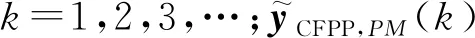
在控制过程中，一般考虑被控量尽量接近期望值并避免控制量剧烈变化，因此在分布式多变量DMC滚动优化中，在k时刻进行第l次迭代计算时，可取全局优化性能指标JC(k)为：

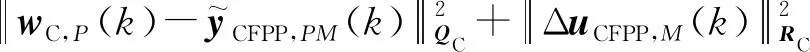
(2)

由于CFPP系统的预测模型和全局优化性能指标均涉及PCC系统还未求解的未来控制增量矩阵ΔuPCC,M(k)，可采用预估迭代算法来解决这一问题，即在第l次迭代中，CFPP系统的预测模型为：

ACPΔuPCC,M,l-1(k)

(3)

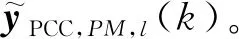
将全局优化性能指标表示为：

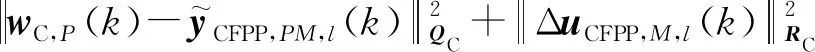
(4)

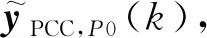
按上述同样的方法可构造PCC系统的全局优化性能指标，计算在迭代时刻l的控制增量ΔuPCC,M,l(k)。

考虑到CFPP-PCC系统中阀门、泵等控制元件的物理限制，对CFPP-PCC系统施加控制量的速率约束(式(5))和幅值约束(式(6))。

Δuj,min≤Δuj≤Δuj,max

(5)

uj,min≤uj≤uj,max

(6)

式中：Δuj,max和Δuj,min分别为控制量变化速率Δuj的上、下限；uj,max和uj,min分别为控制量uj的上、下限；下标j表示CFPP或PCC。

在k时刻，将式(3)代入式(4)，在每个采样周期对性能指标进行最小化，同时考虑控制量的速率约束和幅值约束。通过求解以上预测控制优化问题，得到未来M个时刻内的最优控制增量ΔuCFPP,M(k)，并使当前时刻的控制量uCFPP(k)作用于CFPP系统。按同样方法可计算ΔuPCC,M(k)，并将当前时刻控制量uPCC(k)作用于PCC系统。

在控制量uCFPP(k)和uPCC(k)分别作用于CFPP和PCC系统后，根据预测模型可得到未来P个时刻的被控量预测值。

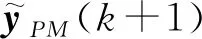
(7)

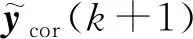
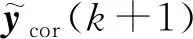
(8)

式中：S0为移位矩阵。

可按上述过程对预测模型进行校正，并基于校正模型开展滚动优化计算。

2.2 分布式预测控制计算流程

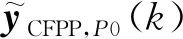
步骤2：每个子控制器接收另一子控制器的前次优化控制增量后，通过最小化全局性能指标，并行求解各自的预测控制优化问题，得到本次迭代最优解ΔuCFPP,M,l(k)和ΔuPCC,M,l(k)。

步骤3：检验2个子控制器得到的最优解是否满足迭代收敛条件，即

(9)

式中：εCFPP、εPCC为指定精度。

若2个子控制器的求解均满足迭代收敛条件，则令ΔuCFPP,M(k)=ΔuCFPP,M,l(k)，ΔuPCC,M(k)=ΔuPCC,M,l(k)，进行步骤4；否则，令ΔuCFPP,M,l-1(k)=ΔuCFPP,M,l(k)，ΔuPCC,M,l-1(k)=ΔuPCC,M,l(k)，l=l+1，返回步骤2。

步骤4：将计算得到的当前时刻控制动作uCFPP(k)=uCFPP(k-1)+ΔuCFPP(k)和uPCC(k)=uPCC(k-1)+ΔuPCC(k)分别作用于CFPP和PCC系统，并代入预测模型，得到此时2个子系统的被控量预测值，通过反馈校正、移位等步骤更新预测模型，为下一时刻的滚动优化做准备。

3 仿真分析

为了验证所建立的分布式MPC对于CFPP-PCC系统的控制效果，分别设置分布式MPC控制器参数。

MPC对CFPP的控制参数：采样时间Ts=30 s，QC=diag(90,10,40)，RC=diag(8 500,200,8 300)，控制步数M=3，预测步数P=20，设置控制变量的速率约束和幅值约束分别为ΔuCFPP,min=[-5 -15 -0.03]T；ΔuCFPP,max=[5 15 0.03]T；uCFPP,min=[20 200 0.4]T；uCFPP,max=[120 600 1]T。

MPC对PCC的控制参数：采样时间Ts=30 s，QP=diag(2×106,3×106)，RP=diag(80,180)，控制步数M=3，预测步数P=20，设置控制量的速率约束和幅值约束分别为ΔuPCC,min=[-20 -10]T；ΔuPCC,max=[20 10]T；uPCC,min=[100 30]T；uPCC,max=[700 250]T。

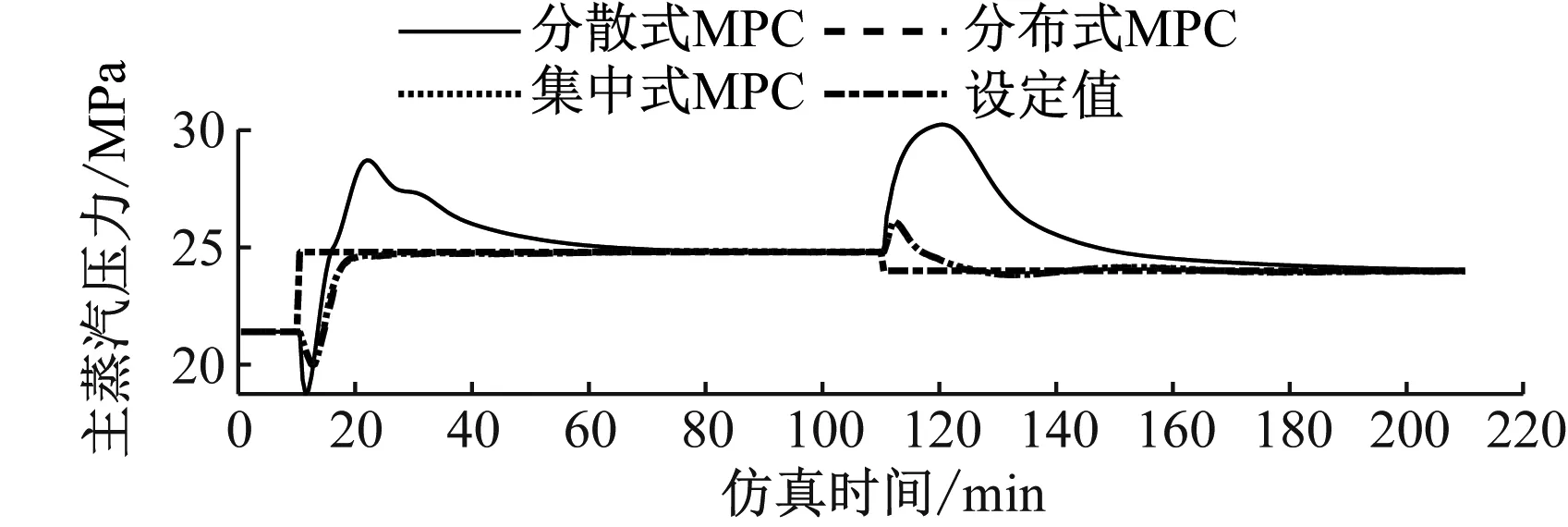
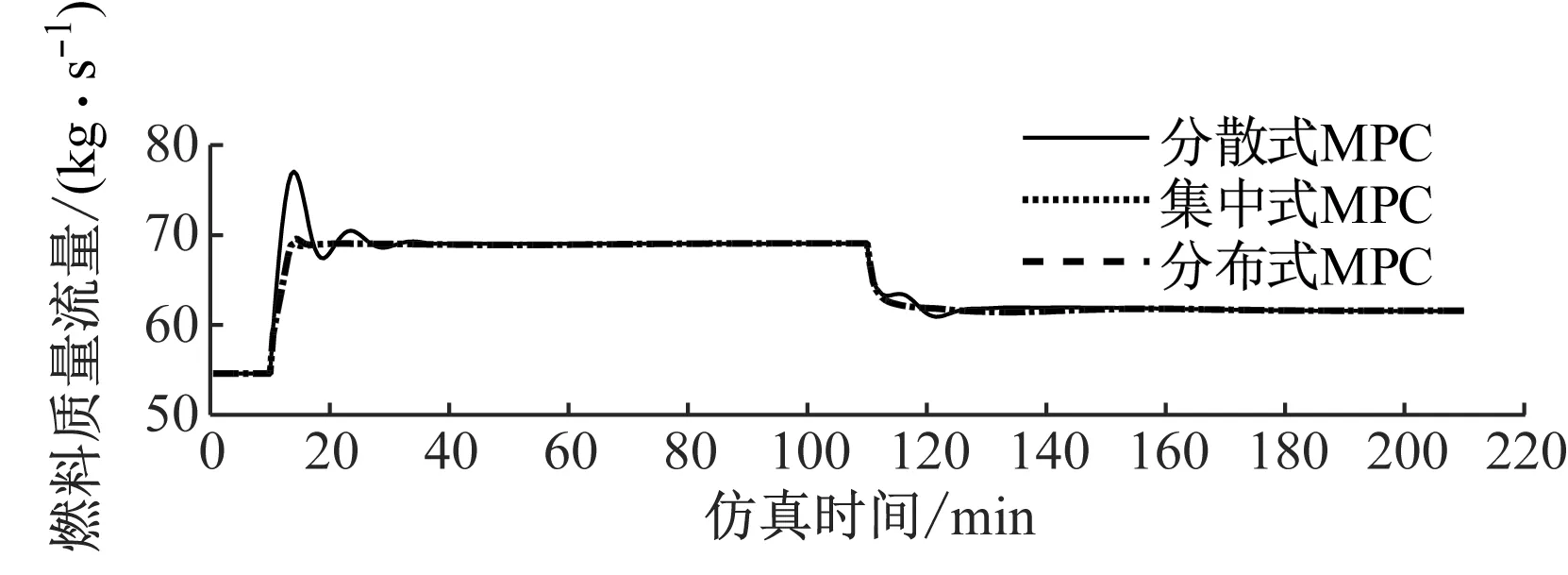
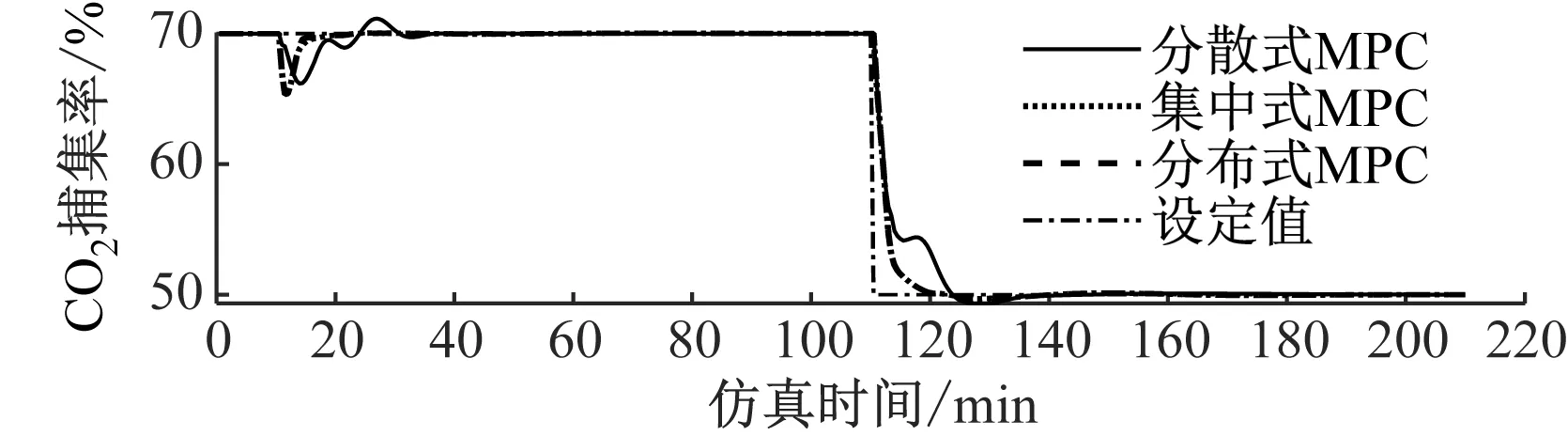
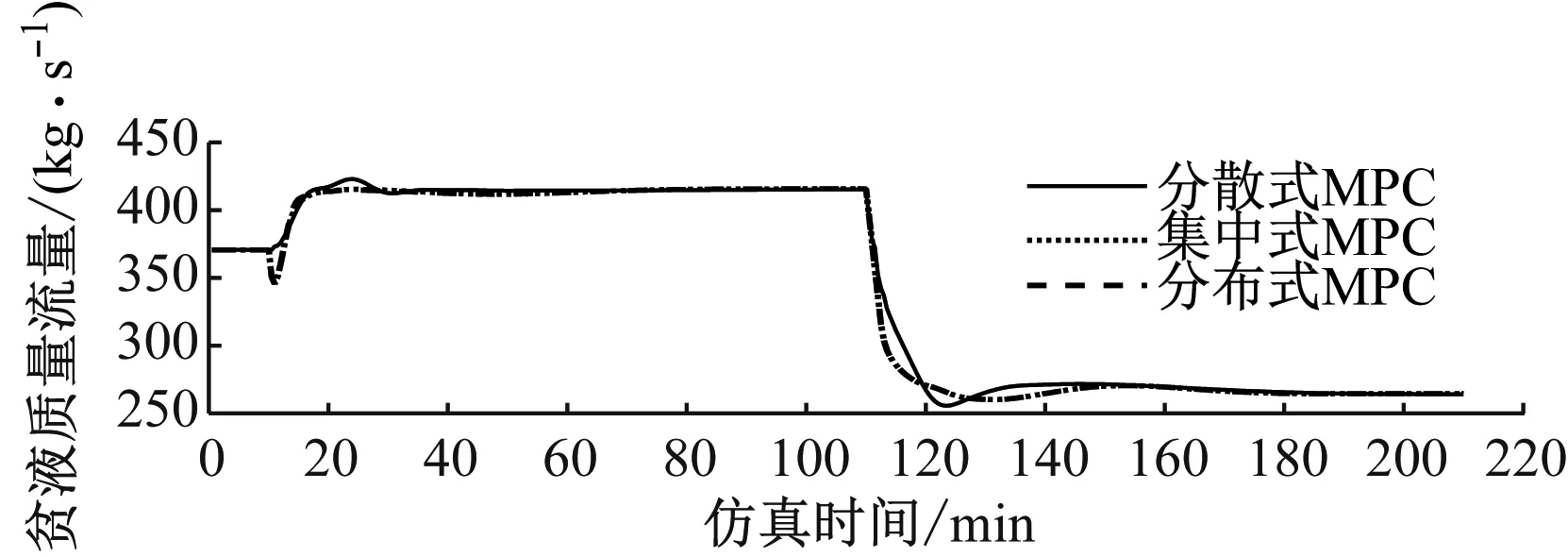
仿真中考虑功率输出和CO2捕集率设定值的变化，来模拟CFPP-PCC系统的运行状况。假设CFPP-PCC系统在稳态工况(见表1)下运行10 min后，功率输出设定值从432.9 MW增大到552.8 MW，主蒸汽压力、中间点焓设定值分别调整为24.8 MPa、2 674.5 kJ/kg，CO2捕集率和再沸器温度分别保持为70%和392.2 K。CFPP-PCC系统再运行100 min后，功率输出设定值降至506.9 MW，主蒸汽压力、中间点焓设定值相应变为24 MPa、2 702.5 kJ/kg，CO2捕集率降低至50%，再沸器温度仍保持在392.2 K。

为了验证所建分布式MPC控制器的有效性，将其与分散式MPC和集中式MPC控制器进行对比，其参数设定与分布式MPC控制器相同。系统总仿真时间为210 min，分布式MPC的每个采样周期迭代计算次数最大值设为5次，迭代终止精度εCFPP=εPCC=0.05，仿真结果如图5～图8所示。

(a)

从图5～图8可以看出，由于分布式MPC考虑了2个系统的相互作用，在每个采样周期通过子控制器间的信息共享及迭代计算保证了整体系统的控制效果。分布式MPC具有与集中式MPC相当的全局最优控制效果，相较于分散式MPC，分布式 MPC能更快、更平稳地调节主蒸汽压力、汽轮机功率以及CO2捕集率，有助于实现整体系统的低碳灵活运行。控制器单次优化所需计算时间如表2所示。由于控制器的分布设计，分布式MPC单次优化计算所需的时间更少，因而在线优化计算效率较高。此外，由于子系统故障一般不会影响全局，分布式MPC具有更高的运行可靠性。

(a)

(a)

(a)

表2 控制器单次优化所需计算时间

4 结 论

基于动态矩阵控制原理建立了煤电站-碳捕集系统的分布式MPC方法。结果表明，分布式预测控制器具有与集中式预测控制器相似的全局最优控制效果，控制性能明显优于分散式预测控制器，且其计算效率高于集中式预测控制器，能够实现电站-碳捕集系统的稳定、低碳及灵活运行。