串列深腔流致声共鸣特性研究

张正凡，王 鹏，*，王炜哲，刘应征

(1. 上海交通大学 机械与动力工程学院 叶轮机械研究所，上海 200240；2. 上海交通大学 燃气轮机研究院，上海 200240)

0 引 言

由于流量分配和流动测量的需求以及空间场地限制等，主管路-侧深腔（或旁支管）的结构布局广泛存在于工业复杂管路系统，如核电一回路系统[1-2]、天然气输运系统[3]和飞机空气分配系统[4]等。此时，主管路来流会在腔体开口处发生流动分离而形成剪切涡脱；当剪切涡脱沿着腔体开口处向下游输运时，一旦与腔体内部固有声模态达成频率锁定和相位匹配[5]，则会发生严重的流致声共鸣现象，从而产生强烈的噪声辐射，甚至引起结构振荡和声疲劳破坏等事故。尤其是对于本文研究的串列深腔来说，上游腔体和下游腔体之间能够形成声学放大效应[6-7]，使得内部的声驻波模态更容易被来流剪切涡脱所激发，从而产生更加严重的流致声共鸣现象。因此，深入研究串列深腔流致声共鸣产生规律，对于相关管路腔体优化布局及其气动噪声抑制等具有重要的理论指导和工程应用价值。

截至目前，国内外已有许多学者针对管路中的单个深腔结构内的流动噪声现象开展了研究。赵伟等[8]采用压力传感器测量了深腔底部压力脉动的变化规律，发现：流致声共鸣的发生使得壁面压力呈正弦波动，并指出流致声共鸣导致的窄带噪声幅值明显高于由剪切层和湍流脉动引起的宽频噪声。East等[9]同样采用单点压力测量的方法研究了腔体压力脉动与来流速度和腔体深度之间的关系，发现：适宜的几何条件和来流下流致声共鸣可以被激发，增大来流雷诺数达一定值时，可以激发更高阶声模态，产生更高频率的流致声共鸣和壁面压力脉动；此外，结果还表明增大腔体深度可以减小压力脉动的窄带频率。Hong等利用LES-FWH模型数值模拟方形、圆形和梯形腔体中的流致振荡，发现方形腔体能够被激发出最强的声共鸣，且腔体长深比越小声共鸣越弱[10]。这些研究揭示了不同管路形状和流动条件下单个腔体中的声共鸣现象的变化规律。

在对多个深腔声共鸣的研究中，Tonon等对多种有双深腔结构的管道进行了研究，指出若使上游腔体深L2、两腔间距L3、下游腔体深L4满足L2=L3(2n-1)/2j=L4(2n-1)/(2i-1) ，i= 1, 2, 3,···；j= 0, 1, 2,3,···；n= 1, 2, 3,···，则发生声共鸣时的壁面压力脉动频率fn=c0(2n-1)/(4L2)，c0为声速[11]。Tonon等研究了带有6个不同深度串列腔体的管道，测量了各个腔体端面压力脉动，发现最强烈的振荡与同一时刻下仅有一个剪切涡出现在腔口的一阶水动力模态有关，同时在6个串列谐振腔中改变部分腔体深度的做法对声共鸣影响十分有限[12]。Avraham、Tonon等总结了流声耦合效应的相关理论和机理，提出了一种利用能量守恒预测自激振荡的模型并将其应用在多种有T形分支的管道系统中[2]。Kriesels等为探究带有可调深度对称深腔的管道中的脉动现象，使用涡团法计算二维流场，使用激光多普勒测速仪（laser Doppler anemometry, LDA）、纹影法得到方管中的速度场，测量了圆、方管端部压力脉动，结果显示圆、方管的测量结果与计算结果十分相近[13]。

在这多种管道布置形式中，双深腔串列管道结构的流致噪声问题得到了部分研究者的关注。Bruggeman等经过理论分析认为发生声共鸣时的声波波长λ与侧腔深度L存在关系：L= (n+1/2)λ/2 ，n=0, 1, 2, 3, ···，并利用LDA、流动可视化、压力脉动测量方法研究了有串列腔体的圆截面和方截面管道中的流动，证实了腔体间距为2倍腔体深度时存在强烈的声共鸣；端面无量纲压力脉动强度随腔体长径比和马赫数变化，但在低马赫数下无量纲压力脉动几乎与马赫数不相关；提高当地声速如采用恰当的扰流板布置，可以将噪声减小30～40 dB[7]；还提出了一种减小下游腔体前缘的曲率半径以增强涡脱落的声吸收作用的方法，指出腔口扰流板的降噪效果取决于辐射和摩擦损失的大小[14]。Ziada等研究了存在声源激励、系统压力0.35 MPa时串列和对称腔体在一定来流马赫数下的剧烈声共鸣现象，认为这种声共鸣的机制与浅腔中旋涡撞击腔口下游弯角的振荡机制不同[15]。

然而，在现有的资料中，很少见到使用管腔壁面多点压力脉动测量方法参照声模态计算结果对双串列深腔流致声共鸣现象进行研究。本文在计算得到理论声共鸣频率的基础上，对串列深腔流致声共鸣现象开展声模态计算和压力脉动测量，利用声模态计算获得了不同腔体间距的管道在各阶模态下的压力时空分布特征，利用动态压力传感器阵列得到了不同来流雷诺数和腔体间距下的腔体压力分布，并将两者进行对比分析，对串列双深腔声共鸣特性随腔体间距变化的规律进行了探究。

1 研究方法

1.1 声学计算

1.1.1 固有声模态

声波在管道、深腔中传播时，会在到达一个腔体端面时发生反射。入射波pi与反射波pr相叠加：

其中：piA为入射波的幅值，prA为反射波的幅值，ω和k分别为该列波的圆频率和波数，t和x分别为时间和空间坐标。当入射波与反射波能量相近时，第一项幅值远小于第二项，第二项占主导，因此在距离壁面x=nπ/k=nλ/2 处振幅最大，而距离壁面x= π(2n+1)/(2k)=λ(2n+1)/4 处振幅为零(n为自然数)。声压振幅与坐标有关，在管腔中形成了驻波[16]。

在串列深腔中，若要能够维持自激振荡，需要驻波模态的驻波波节位于深腔开口的T形接头处，否则由于T型接头处空气振荡向上下游辐射能量，导致模态不能被激发，于是发生强烈声共鸣时的声波波长λn= 2L/(n+1/2)，n= 0, 1, 2,···。n= 0时，有λ0= 4L[7,14]；n= 1时，有λ1= 4L/3 =λ0/3。295 K时，空气声速c1=346 m/s，可以计算出一阶驻波模态频率f0=c1/λ0≈540.6 Hz和二阶频率f1=c1/λ1= 3f0，取基准频率f0=540 Hz对峰值频率无量纲化。

在特定腔体间距布置下，一定流速的流体流过串列深腔开口能够激发对应特定声波频率f的驻波模态cn。不同模态阶数n对应不同波长λ、模态频率f=c/λ和不同的管腔壁面压力分布。

1.1.2 声学有限元

建立管腔结构的几何模型，在LMS Virtual.Lab中作声学计算。对所用的管腔模型腔体的上下游管道做了延伸，紧邻布置上下游管道长都为5.4L，其他布置上下游管道长分别为7.5L、12.5L，其余尺寸与试验模型相同（见1.2.1节）。

空气压力脉动可以分为流动成分与声压成分。由于在计算模型中不存在流动，可以将计算得到的压力场视为声压场，即只有声音成分的压强时空分布。在给定的管腔结构中，特定波长的声波可以形成驻波，驻波形成时管腔内声压分布关于时间坐标和空间坐标是解耦的，每个位置处的声压都以特定幅值和周期做简谐振荡。计算得到的声模态展现了各个不同频率的驻波及其声压分布，声压分布为压力脉动达到峰值时的压力空间分布。

采用默认的全反射边界条件，计算频率范围为200 ～ 2 800 Hz。取每种串列深腔布置的第一阶（C1:f≈f0）和第二阶（C2:f≈ 3f0）驻波模态作分析。

1.2 试验测量

1.2.1 试验设备与测量方法

使用带有串列双深腔的管道作为试验段流道（图1），其中腔体宽Dc= 32 mm，管道和腔体垂直于纸面的厚度和主流管道截面高为Dm= 1.25Dc，腔体深度L满足L/Dc= 5。4种布置的两深腔中轴之间的间距D1满足D1/λ=D1/(4L) = 1/16、1/4、1/2、3/4[14]。本文将D1/λ= 1/16的腔体布置称为紧邻布置，而将D1/λ= 1/2的布置称为半波长布置。

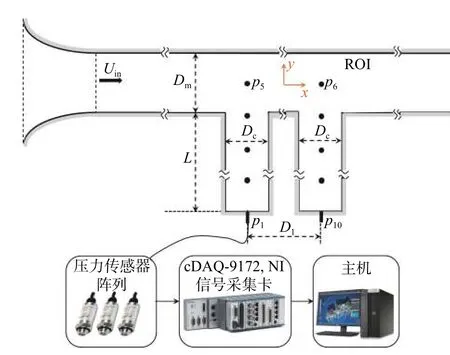
图1 管道及测量设备示意图Fig. 1 Schematic of pipeline and auxiliary equipment

试验段入口上游主管道壁面开有一孔，可以用于测量来流的静压，也可以插入毕托管测量入口流速。使用数据采集卡和压力传感器实现连续压力测量。流道侧壁共有10个动态压力测点，每侧腔体5个，从腔体端面到腔体与主管道轴线交点均匀排布。4种腔体间距的测点布置相同。测点处壁面开有测压孔，高灵敏度动态压力传感器（PCB，USA）插入测压孔测得动态压力信号。信号通过BNC线被传给采集卡（cRIO-9 039，NI Labview，USA），之后通过USB线被传给主机并由主机保存测量数据[17-19]。利用预先标定的传感器系数换算，可以获得入口静压和10个测点的压力脉动。

空气在涡声耦合试验台和抽气泵之间循环，通过稳定段、收缩段和滤网的处理以尽可能接近层流的状态流入试验段。试验前标定风洞内风速，以获得风机频率和来流速度的换算系数。

使用腔体间距不同的4种管道布置进行试验，对每一种布置，在不同入口风速下测定压力脉动。在特定工况的特定时刻下，由10个传感器测量到的10个压力值，可以得到该时刻的驻波波形。

1.2.2 数据处理

为了便于测量声共鸣发生时的管腔压力分布并分析其特征，需要选取流致声共鸣较剧烈的工况，并与声共鸣较弱的工况相对比。选取压力脉动最强的测点（由测量结果可知为腔体端面上的测点1、10，实际使用测点1）的数据，绘制无量纲化压力脉动均方根值pRMS/(0.5ρuin2)随来流雷诺数Rein=UinDm/v1和腔体间距D1变化的图象，其中ρ是295 K时空气在入口静压下的密度，v1为295 K下的空气动力黏度。

从无量纲化压力脉动时均值变化曲线上选取部分工况作进一步研究。利用FFT变换将压力脉动信号转换到频域上，绘制幅频曲线。测量时的采样率为50 kHz，采样时长大于1 s，故频域的范围为1 ～ 25 kHz。通过识别幅频曲线极值点可以得到压力脉动的特征频率，并算出脉动周期。

为刻画流速随峰值频率的变化，将每个腔体间距下的所有工况的峰值频率各自绘在一张图中。选取部分工况，绘制一个周期内10个测点压力的时空分布图以描述声共鸣被激发时的压力时空变化特征，将瞬态压力p用入口动压0.5ρuin2无量纲化：p/ (0.5ρuin2)。

2 结果与讨论

Peters等[20]指 出，当 腔 体 间 距 为D1=mλ/2 =2mL，m= 0, 1, 2,···， 管道中的驻波模态可以被激发并产生声共鸣现象。以下详述D1＜ λ 的4种情形，包括D1=λ/16（紧邻布置）、λ/4、λ/2 （半波长布置）、3λ/4。

2.1 串列腔体声学驻波模态

声模态计算结果为压力云图，为获得一般性的压力分布特征，用pmax将压力pa无量纲化（图2）。

D1=λ/2时，管道的一阶驻波模态频率与理论值非常接近，相差仅1.43%。这里与腔深为λ/4相配套的半波长布置使得驻波波节恰好位于T形接头处，不会由于T形接头处的振荡导致驻波模态能量向上下游辐射，因此能够维持驻波[14]。

D1=λ/16时，声模态计算一阶驻波模态频率为489.6 Hz，低于根据二倍深腔深度2L推算的理论值f0约10%；而根据加入腔体间距的驻波波长λ0=2(2L+D1)推 算 的 一 阶 驻 波 模 态 频 率 为=c/λ0≈480.556 Hz，声模态计算结果与仅相差1.8%。二阶驻波模态频率也存在相同的情况。因此在计算紧邻布置管腔结构的实际声模态频率时需要将腔体间距纳入考量。

D1=λ/4 时，一阶驻波模态频率相距基准频率比紧邻布置更远；从图2中可以看出D1=λ/4时一阶模态下向主流管道的行波辐射较为严重，其在实际流动中将无法维持驻波。D1= 3λ/4的情形与D1=λ/4相似，由于驻波波节不位于T形接头处，使得驻波模态因沿管道的能量辐射不能被强烈地激发。

图2 各腔体间距下的管腔声模态：(a) D1 = λ/16（紧邻布置），(b) D1 = λ/4，(c) D1 = λ/2（半波长布置），(d) D1 = 3λ/4Fig. 2 Acoustic modes of tubes with different distances between cavities: (a) D1 = λ/16, (b) D1 = λ/4, (c) D1 = λ/2, and (d) D1 = 3λ/4

此外，注意到一阶驻波模态有两种情形：两腔体振荡同相与反相。在D1=λ/16、λ/4时（图2（a、b）），一阶驻波模态表现为两腔内反相位振荡；由于腔体之间管道很短，对于波腹位于主管道的驻波模态，腔口的压力脉动产生向上下游的能量辐射，无法维持自激振荡，两腔同相位的驻波模态不会被激发。在D1=λ/2、3λ/4时（图2（c、d）），一阶驻波模态表现为两腔内同相位振荡，诱发两腔间主流管道内反相位振荡；若其驻波模态波节位于主管道中央，则会导致T形接头位置的振荡幅值过大，驻波的能量向上下游辐射，因此两腔反相位的驻波模态无法被激发。主流管道的波腹处声压脉动峰值低于腔体端面脉动峰值，可能与声波能量沿主管道传播有关。

2.2 压力脉动频谱分析

图3为4个不同腔体间距的管道中第一个测点即上游腔体端面处的无量纲化压力脉动随来流速度的变化。紧邻布置和半波长布置在一定流速下被激发出了强烈的声共鸣，而这种现象在另两种管道中并未出现。

提取紧邻布置和半波长布置的各个来流雷诺数下的声压脉动主频展示在图4（a、b）中，其中剔除了环境低频噪声占主导的工况，cn=1、2分别表示一阶或二阶驻波模态被更强烈地激发。将图3与图4（a、b）对照，在较大的雷诺数范围下，声共鸣主频与理论值（1.1.1节）很接近，可能是由于紧邻布置的一阶驻波模态被激发，但其腔体间距导致了模态频率与基准频率约10%的偏差。从图3可以看到f≈ 3f0时声共鸣幅值已经很小，可能是由于高阶模态被激发所产生的声共鸣可以被忽略。

图3中，半波长布置的振荡幅值略大于紧邻布置，这可能是由于紧邻布置的一阶模态的波节不严格位于T形接头处，该处的压力脉动造成的声能辐射使其一阶驻波模态的能量稍弱于半波长布置。

图3 上游腔体端面的无量纲化压力脉动RMS值与来流雷诺数的关系Fig. 3 Relationship between the RMS value of dimensionless pressure pulsation at the endplate of the upstream cavity and the inflow Reynolds number

除了存在D1=nλ/2 (n= 0, 1, 2,···) 驻波模态被激发时的频率锁定现象外，还可能存在峰值频率f、来流雷诺数Rein的正相关关系（图4（a、b））。当D1=λ/4或3λ/4，驻波模态没有被强烈地激发时，这种相关性更为明显。D1=λ/4 的结果中St数分布在0.32～0.45和0.66～0.79两区间（图4（c）），中位数分别为0.39和0.74；D1= 3λ/4 的St数分布在0.3～0.44和0.65～0.8两区间（图4（d）），中位数分别为0.38和0.74；二者的St数均与Bruggeman等所得的StH=(0.4±0.02)(n+1)较为接近[14]，其中St=fDc/Uin。这里可能存在低马赫数、高来流雷诺数下与腔口剪切层振荡有关的流体动力学模态或涡脱落模态[14-20]，其模态频率与来流雷诺数成正比。流体动力学模态的相关情况还有待后续进一步研究。

图4 不同工况下的峰值频率分布及其对应的模态Fig. 4 Peak frequency distribution under different distances of cavities spacing and acoustic modes

2.3 声共鸣波形分析

为了验证管道中发生声共鸣时其内部压力分布符合声模态计算得到的驻波模态结果，这里给出了D1=λ/16和λ/2 的声模态计算与试验结果的腔体压力分布对比（图5）。分别取图3中所选工况下幅值最大的相位的压力测量数据和声模态计算输出的数据，并用各自的最大压力脉动峰值进行无量纲化处理，得到波形对比图。

两种布置在所选工况下测得的压力分布证实了这些工况下所激发的模态均为一阶驻波模态。紧邻布置下声压测量与声模态计算结果吻合较好（图5（a））。声模态计算所得压力在两腔体间管道的中央幅值为0，并向两个腔体端面逐渐增大，与试验结果、理论分析中的n= 1的情形及Ziada等[21]的结论相符，证明了它的有效性。注意到测量数据的左侧幅值大于右侧，可能与不同的两腔体流动条件、涡强度等因素有关。

半波长布置下试验与声模态计算得到的压力分布不存在较大偏差（图5（b））。该布置试验结果受实际流动中剪切层振荡、涡脱等可能的因素影响，不是完全对称的，但对称性稍好于紧邻布置。

图5 紧邻腔体和半波长间距腔体一阶模态的测量结果与声模态计算结果的比较Fig. 5 Comparison of measurement and simulation results of the 1st acoustic mode of the close-proximity duct as well as the half-wavelength duct

由于不同的工况下管道声共鸣特性可能有较大不同，选取7个工况（图3），提取这些工况下测得的一个周期内的壁面压力数据，得到壁面压力的时空分布图（图6、图7），从图中可以对这些工况下的腔体壁面压力脉动特性有直观了解。

图6 紧邻布置下的管壁压力时空分布Fig. 6 Spatio-temporal evolution of wall pressure at D1≈0

图7 半波长布置下的管壁压力时空分布Fig. 7 Spatio-temporal evolution of wall pressure at D1 = λ/2

对于紧邻布置，随着来流雷诺数逐渐增大，一阶驻波模态被激发，腔体端面压力脉动不断增强，在Rein= 1.17×105时最为剧烈，幅值可达2～3倍入口动压，产生的声共鸣也十分强烈（图6（a））；在来流雷诺数继续增大时，脉动幅值有所降低，在达到入口动压一半后（图6（b）），小幅回升并达到一个新的略大于入口动压一半脉动强度的峰值（图6（c）），随后压力脉动逐渐减弱。在此过程中始终为一阶驻波模态占主导，且两腔振荡相位相反，波节位于深腔开口附近。

在半波长布置中，随着来流雷诺数增大（图3），一阶驻波模态被激发，Rein= 0.61×105时出现第一个压力脉动峰值（图7（a）），腔体端面压力脉动幅值接近入口动压；随后声共鸣快速削弱，但在来流雷诺数进一步增大时重新增强并在Rein= 1.26×105处变得十分强烈，压力脉动峰值达到2倍入口动压的最大值（图7（b））；之后压力脉动快速减弱，但在Rein=1.56×105处脉动幅值约为0.5倍入口动压时（图7（c））脉动幅值下降速度放缓；在达到Rein= 1.78×105时脉动幅值仍接近0.5倍入口动压（图7（d）），这是二阶驻波模态被激发的结果，一阶驻波模态已不占主导。一阶和二阶驻波模态分别在不同的来流雷诺数下被激发并产生强烈的声共鸣现象，这与紧邻布置仅一阶模态被强烈地激发有所不同。在前两阶驻波模态被激发时，两个深腔中的振荡相位始终相同。

3 结 论

本文使用4个腔体间距不同的串列双深腔的管道模型布置，对不同布置下管道的压力时空分布进行了声模态计算，并对各布置在不同来流雷诺数下的管腔侧壁压力脉动进行了试验测量。试验得到了各布置在不同工况下的特征频率，并对比声模态计算和测量得到的压力脉动波形、分析几个不同工况下的压力时空分布，验证了所激发的模态为驻波模态，初步揭示了不同腔体间距串列深腔内的声共鸣规律，主要得到了以下结论：

1）压力脉动均方根值的变化表明，在合适的腔体间距（半波长布置和紧邻布置）下，串列腔体内一阶驻波模态能够在较宽的速度范围内被激发，压力脉动幅值保持在较高水平，脉动时均值可以超过入口动压；而二阶驻波模态仅在半波长布置下被强烈地激发，其强度弱于一阶模态被激发时，但时均值仍可达0.4倍入口动压。半波长布置的压力脉动强度最高，其次为紧邻腔体布置，它们的声共鸣现象最为剧烈；λ/4、3λ/4间距布置的压力脉动强度始终在中等或更低水平（10-3～10-1倍入口动压）。

2）对特定腔体深度和截面下串列腔体间距不同的管道，用不同方法得到了相近的流致声共鸣模态频率。利用文献中给出的声共鸣频率计算方法计算了本研究中的腔体声共鸣的理论一阶驻波模态频率[11]。频率理论值与半波长布置的声模态计算结果十分相近而与紧邻腔体布置有少许偏差；腔体间距非λ/2整数倍的管道不满足发生声共鸣的几何条件，驻波模态不能被强烈地激发，这在实验中得到了印证。试验得到的声共鸣频率与声模态计算结果吻合较好。紧邻和半波长布置在不同的来流雷诺数下被激发出的前两个声共鸣主频分别对应于声模态计算所得一阶和二阶驻波模态频率。

3）压力脉动时空分布显示驻波模态被激发时，波腹位于腔体端面，而波节总位于T形接头处。紧邻布置的两个深腔内部声压脉动反相位振荡；半波长布置的深腔声压脉动同相位振荡，诱发主管路声压反相位振荡。声模态计算结果中主流管道波腹位置的压力振荡幅值略小于腔体端面。压力脉动测量得到的压力时空分布验证了声模态计算的结果。