基于自抗扰控制的永磁同步电机矢量控制系统研究＊

林立 ， 吕金培 ， 林敏之

（1．多电源地区电网运行与控制湖南省重点实验室，湖南 邵阳，422000；2．邵阳学院电气工程学院，湖南 邵阳，422000；3．邵阳资水科技有限公司，湖南邵阳，422000）

永磁同步电机（Permanent Magnet Synchronous Motor，PMSM）因具有体积小、效率高、功率密度高等优点，已广泛应用于医疗器械、数控机床、电动汽车、航空航天等行业[1-3]。然而永磁同步电机本身是一个具有多变量、强耦合、非线性和可变参数的复杂系统[4]，在实际应用中，永磁同步电机的发展受其结构和控制电路性能的影响，良好的控制系统可以显著提升其性能。

目前，针对PMSM控制技术应用最多的当属PID控制，结合PMSM矢量控制理论，已能够满足绝大多数控制场合要求，然而其响应速度和超调量两者之间不可调和的矛盾也制约着PI技术在高精度控制场合的应用[5]。随着科学技术的不断进步，对于控制性能的要求越来越高，高精度控制领域中PID难以处理复杂控制对象的缺陷逐渐显露出来[6]。现代控制理论产生并涌现出了如最优控制、鲁棒控制、自适应控制等理论成果，大部分的现代控制理论方法均依赖于系统的数学模型，在实际应用中有局限性[7]。为实现高性能控制，提高系统的控制精度、鲁棒性和响应速度。模糊控制、预测控制、滑模控制和自抗扰控制等先进控制策略不断被提出，其中，ADRC独立于被控对象的数学模型，因其响应速度快、控制精度高，在电力系统、加工车床等领域得到了广泛应用。

然而，传统ADRC因非线性fal函数在原点和断点附近的平滑度不好、控制器的调整参数较多、参数整定困难等问题，降低了ADRC的控制性能。本文正是基于此提出了一种优化的自抗扰控制器，并应用于矢量控制的速度环，通过对传统ADRC和改进ADRC进行对比仿真验证，改进ADRC控制系统控制精度高、抗干扰能力强、响应速度快。

1 标准ADRC模型原理分析

ADRC是源于PID技术发展而来的、且不依赖被控对象，尤其在要求实现高速高精度控制的场合，与PID相比，ADRC的控制精度和抗干扰能力更佳。ADRC由3部分组成：跟踪微分器（Tracking Differentiator，TD）、扩张状态观测器和非线性误差反馈控制律，如图1所示。

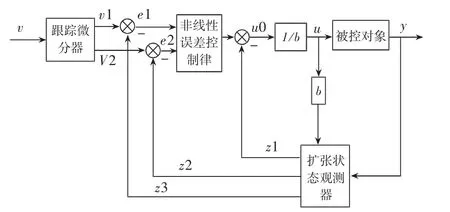
图1 ADRC控制示意图

1．1 跟踪微分器

其中，TD是一个过渡过程，为了防止目标值突变，使输入信号突变部分变得平滑。TD的状态方程可用式（1）表示：

式中，x1、x2为系统状态，v（k）为输入信号，r0为决定跟踪快慢的参数，h为积分步长，h0为滤波因子，fhan函数为最速控制综合函数。其中r0的值越大，跟踪的速度也会越快，r0的值过大会使跟踪信号与原信号重叠；h0的值越大，响应速度会随着h0的值增大而减小。

1．2 扩张状态观测器

ESO是自抗扰控制的核心部分，用于观测系统中产生的未知外扰动和内扰动，对系统各状态和未知扰动进行跟踪估计，并对其进行补偿。其状态方程如下：

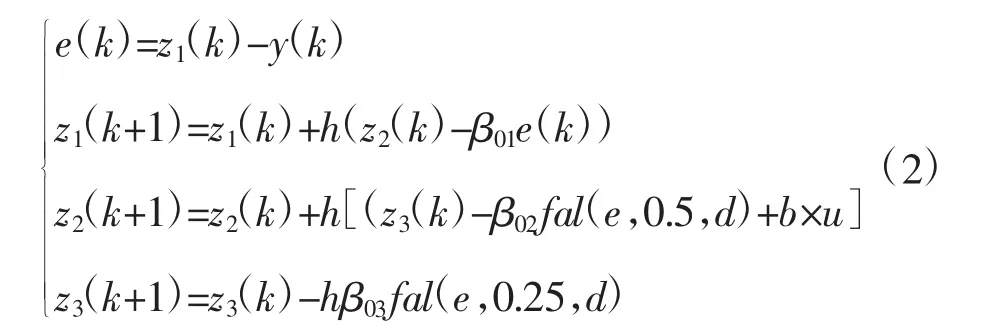
式中，z1（k）、z2（k）、z3（k）为ESO的三个输出，z1（k）的数值是跟随着输出y的，z2（k）是跟随y的微分的，z3（k）是系统扩张的一个状态，它对系统的总扰动观测并进行一定的补偿。

1．3 非线性误差反馈控制律

NLSEF是由跟踪微分器产生的跟踪信号与状态观测器观测系统输出值之间的误差e1以及对给定信号的微分与系统输出的导数得到的误差e2来进行控制和扰动补偿的：

式中，e1、e2分别为误差和误差积分，d为滤波因子，β1、β2为控制器可调增益参数，α为非线性因子。以上提到fal的函数表达式为：

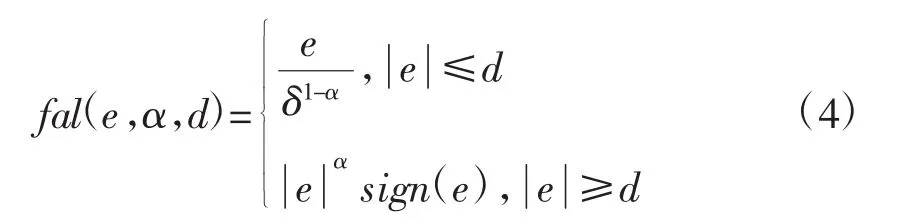
fal函数具有大误差小增益、小误差大增益的特点，在（-∞，-d）、（d，+∞）为非线性区间，在（-d，d）为线性区间，在-d和d两点出现函数拐点。

2 基于改进ADRC技术的PMSM建模

传统ADRC控制中，ESO和NLSEF包含fal函数，该非线性函数存在拐点、系统整定参数较多、参数整定困难，导致系统精度降低，在高精度的控制系统中难以得到应用。针对上述问题，本文采用线性控制律代替非线性误差控制律简化了控制器模型，又利用一种平滑性较好的sigfal函数对ESO的fal函数进行了替换。采用以上两个措施在标准ADRC技术上进行改进，以提升ADRC控制精度。sigfal函数的状态方程如下式所示：

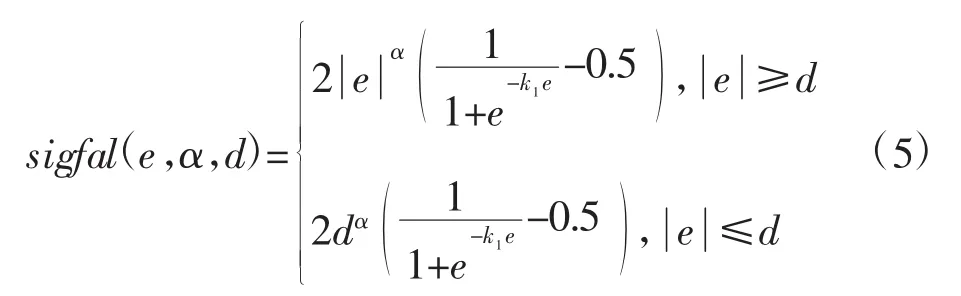
式中，e、α、d分别为偏差、非线性因子、滤波因子，在 sigfal函数中，取 k1＝1／d，可保证该函数的平滑性。

改进ADRC控制结构如图2所示，改进ADRC的 ESO状态方程如式（6）：

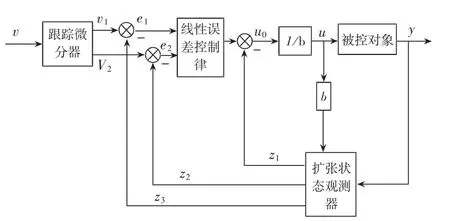
图2 简化二阶ADRC结构图

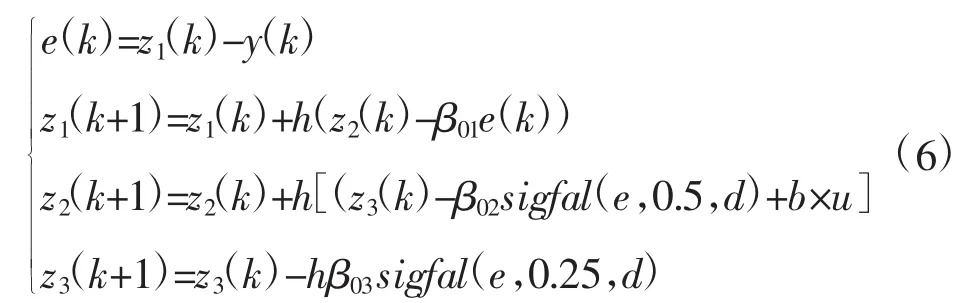
非线性误差反馈控制律中，利用非线性函数fal生成控制信号实现无静差调节，系统整体调参的难度较大。采用线性控制律代替非线性误差反馈控制律，参数整定更容易，工作效率可以得到提高。线性控制律对TD和ESO的输出信号做差，产生误差e1和e2，误差通过比例微分得到u0，再结合扰动补偿分子生成控制信号u，其公式可表示为：

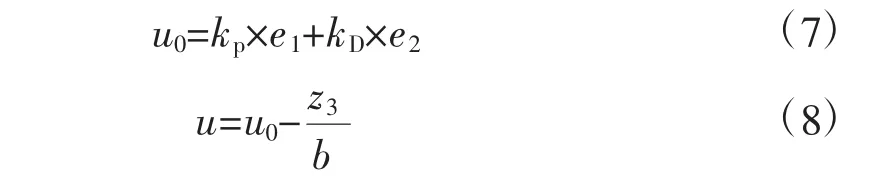
式中：kP为比例系数、kD为微分系数。

3 基于改进ADRC的速度控制器设计与仿真

在MATLAB／Simulink仿真软件中对基于改进ADRC永磁同步电机矢量控制系统进行了模型搭建，在双闭环控制系统中，速度环采用改进ADRC、电流环采用PI控制，并将其与基于传统ADRC的永磁同步电机矢量控制系统在空载和负载条件进行了仿真对比研究。控制系统的整体框图如图3所示。

图3 改进型ADRC的PMSM矢量控制框图

在空载条件下，系统给定转速设为1000，仿真波形图如图4和图5所示。

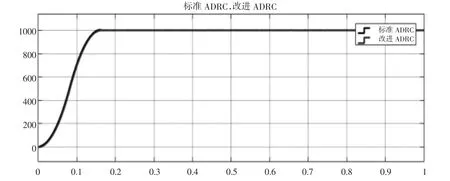
图4 空载条件下改进型ADRC与标准ADRC对比图

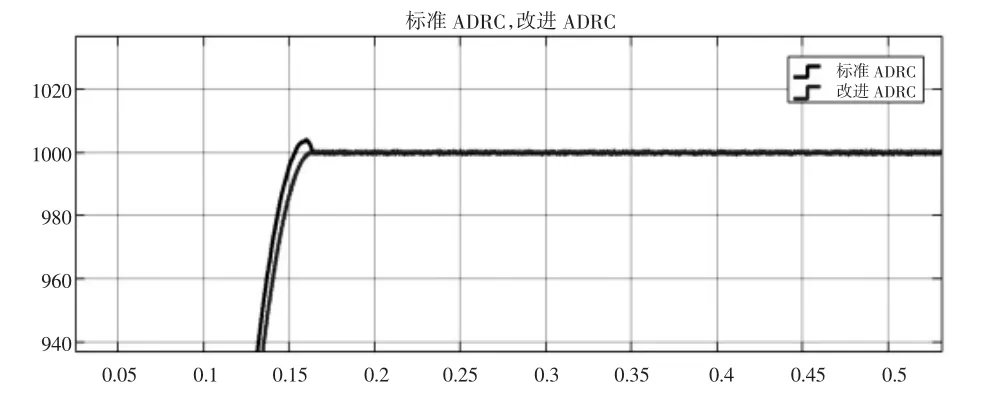
图5 空载条件下改进型ADRC与标准ADRC对比放大图

如图所示，改进型ADRC控制系统和标准ADRC控制系统相比，改进型ADRC控制系统的超调量约为0．06%，比标准ADRC控制系统超调量降低了 0．34%；调节时间约为 0．159s，比标准 ADRC 控制系统调节时间减少了0．005s。由此可见，改进型ADRC控制系统响应速度更好、超调更小、性能较为优越。

在负载条件下，系统给定转速设为1000，在0．5s给系统施加了一个20Nm的负载，仿真波形图如图6和图7所示。

图6 带负载条件下改进型ADRC与标准ADRC对比图

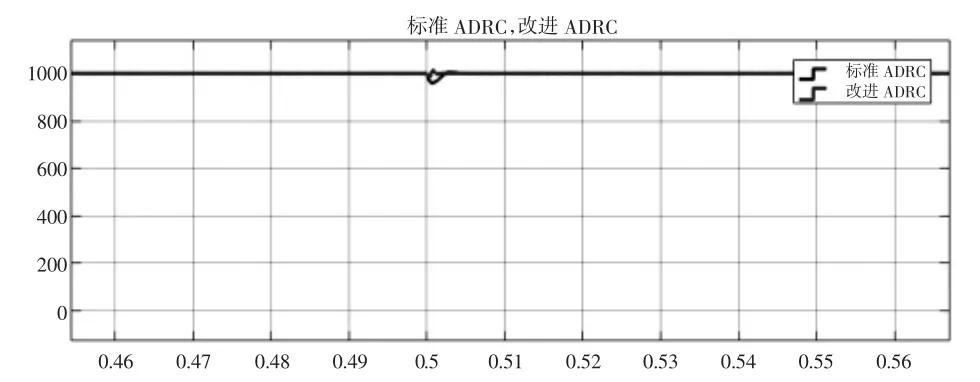
图7 带负载条件下改进型ADRC与标准ADRC对比放大图

如图所示，改进型ADRC控制系统和标准ADRC控制系统的速度响应曲线都有一定的超调，相比之下，改进型ADRC控制系统的超调量较小，比标准ADRC控制系统的超调量降低了1．11%；改进型ADRC控制系统的调节时间约0．0024s，比标准ADRC控制系统的调节时间减少了0．003s。因此受到负载扰动时，改进型ADRC抗负载扰动能力强、系统的控制精度更精准，可以使系统具有更好的抗扰动能力。

4 结论

本文针对标准ADRC中的fal函数拐点处不平滑、容易引起系统抖振而导致系统控制精度提升难的问题，提出了一种改进型ADRC控制器，并在空载和负载条件下，对改进型ADRC控制的PMSM矢量控制系统和标准ADRC控制的PMSM矢量控制系统进行了仿真对比。仿真结果表明，改进型ADRC控制比标准ADRC控制动态响应时间短、参数整定更容易、系统抗负载扰动的能力更强、具有更高的动态性能。