压水堆辐照后燃料中子源强计算方法研究

陈 军，彭良辉，杨伟焱，汤春桃，毕光文，杨 波，姚进国，王 瑞，陈丽培

(1.上海核工程研究设计院有限公司，上海 200233；2.国核示范电站有限责任公司，山东 荣成 264312)

由于核设施在安全性和经济性方面需求，次临界状态下的堆芯反应性测量技术一直是国际上研究的热点[1]。次临界棒价值测量方法是在次临界状态下的堆芯反应性测量技术基础上发展的新一代控制棒价值测量技术，其与临界后低功率阶段动态棒价值测量方法相比的显著区别是：临界前堆芯中子通量水平较低，堆内固定外中子源对通量分布的影响十分显著[2]。因此，准确模拟堆内固定外中子源的源强，是获得高质量中子通量分布预测值的先决条件。对于次临界商用压水堆堆芯，堆内固定外中子源主要有初级中子源、次级中子源和辐照后燃料中子源。其中，辐照后燃料中子总源强与初级中子源强或次级中子源强相当，且具有更复杂的空间分布效应和燃耗历史效应。因此，准确计算辐照后燃料中子源强是次临界棒价值测量技术的基础，具有重要的应用价值。

辐照后燃料中子源由辐照后燃料中的锕系核素或其他被活化核素通过自发核反应产生，主要包括自发裂变中子源和(α,n)中子源[3]。目前，工业界广泛采用点燃耗程序ORIGEN[4]完成辐照后燃料组件中子源强的计算[5-6]，这种方案简单便捷，但存在以下缺点：通常基于平均燃耗历史，由点燃耗模型开展计算，不能精确考虑对辐照后燃料中子源强有重要影响的反应堆空间效应和实际运行历史效应，势必引入较大不确定度。为解决上述问题，本文首先使用堆芯计算程序中的微观燃耗模型计算辐照后燃料中的锕系核素核子密度，其次对辐照后燃料中子源强计算的理论模型进行研究，并基于自主开发核设计程序系统[7-8]开发辐照后燃料中子源强计算功能，精确考虑反应堆空间效应和实际运行历史效应，获得堆芯精细的三维节块辐照后燃料中子源强，为次临界棒价值测量方法的研发奠定基础。

1 理论模型

1.1 堆芯计算程序微观燃耗模型

锕系核素核子密度的获取是辐照后燃料中子源强计算的基础。自主开发的堆芯计算程序对锕系核素采用基于微观燃耗的修正方法考虑燃耗历史效应[8]，即实时求解锕系核素燃耗方程获得核素精确的核子密度，继而计算材料宏观截面。微观燃耗修正方法是微观燃耗方法的改进，具有精度高、易于进行重要核素核子密度跟踪和停堆衰变计算等优点。

微观燃耗修正方法的计算式为：

(1)

(2)

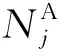
为满足自发裂变和(α,n)中子源强计算需求，在自主开发核设计程序实时跟踪的锕系核素中增加242Cm和244Cm，涵盖重要的自发裂变和α衰变锕系核素。

1.2 自发裂变源强计算方法

可自发裂变的核素i的自发裂变源强为：

Qsf,i=Niλcsfυp1024V

(3)

其中：Qsf,i为自发裂变源强，s-1；Ni为核子密度，cm-3；λ为衰变常量，s-1；csf为自发裂变分支比；υp为每次自发裂变平均释放中子数；V为系统体积，cm3。

此外，考虑停堆衰变反应后的自发裂变源强为：

Qsf,i=Ni,0e-λtλcsfυp1024V

(4)

其中：Ni,0为可自发裂变的核素i停堆时刻的核子密度，cm-3；t为停堆后经历时间，s。

式(4)中的自发裂变数据包括衰变常量、自发裂变分支比和每次自发裂变平均释放中子数，可从评价核数据库获取，表1列出了本文考虑的12种锕系核素的自发裂变参数[9]。

表1 主要锕系核素自发裂变参数Table 1 Spontaneous fission parameters of main actinide nuclides

1.3 (α,n)源强计算方法

堆内α粒子的来源主要为238Pu、239Pu、240Pu、241Am、242Cm和244Cm等锕系核素的α衰变。在这些核素中，242Cm的贡献占据主导，是堆内α粒子的主要来源[10]。α粒子可与重核发生(α,n)反应产生中子，图1给出了不同富集度辐照后燃料中的(α,n)源强占总中子源强比例随燃耗的变化。换料循环绝大部分旧料燃耗超过20 000 MW·d/tU，可见绝大部分辐照后燃料(α,n)源强占辐照后燃料总中子源强份额均小于15%，且随燃耗单调减小。其次，由于实际运行堆芯辐照后燃料直接计算(α,n)源强需先计算α衰变母核核子密度得到α粒子源强，再计算α粒子与各种重核的(α,n)反应率得到中子源强，过程相对复杂。为此，本文基于(α,n)源强与自发裂变源强之比提出以下两种(α,n)源强近似计算方法。

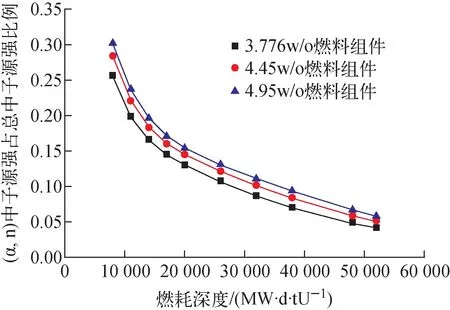
图1 不同富集度燃料组件(α,n)源强占辐照后燃料总中子源强比例随燃耗的变化Fig.1 Ratio of (α,n) to fuel total neutron for different enrichment assemblies vs burnup

方法1为242Cm近似法。该方法近似认为(α,n)源强主要由242Cm产生，忽略其他核素产生的(α,n)源强。利用ORIGEN程序产生典型压水堆3种不同富集度再入堆组件停堆不同衰变时间242Cm产生的(α,n)源和自发裂变源，列于表2。由表2可知，不同富集度组件在不同衰变时间点242Cm产生的(α,n)源和自发裂变源之比稳定在0.191附近。因此，242Cm近似法通过在242Cm产生的自发裂变源强基础上乘以系数0.191来近似考虑堆内(α,n)源强。由于忽略242Cm以外的其他核素的贡献，因此可预见使用该方法得到(α,n)源强将相对偏小。

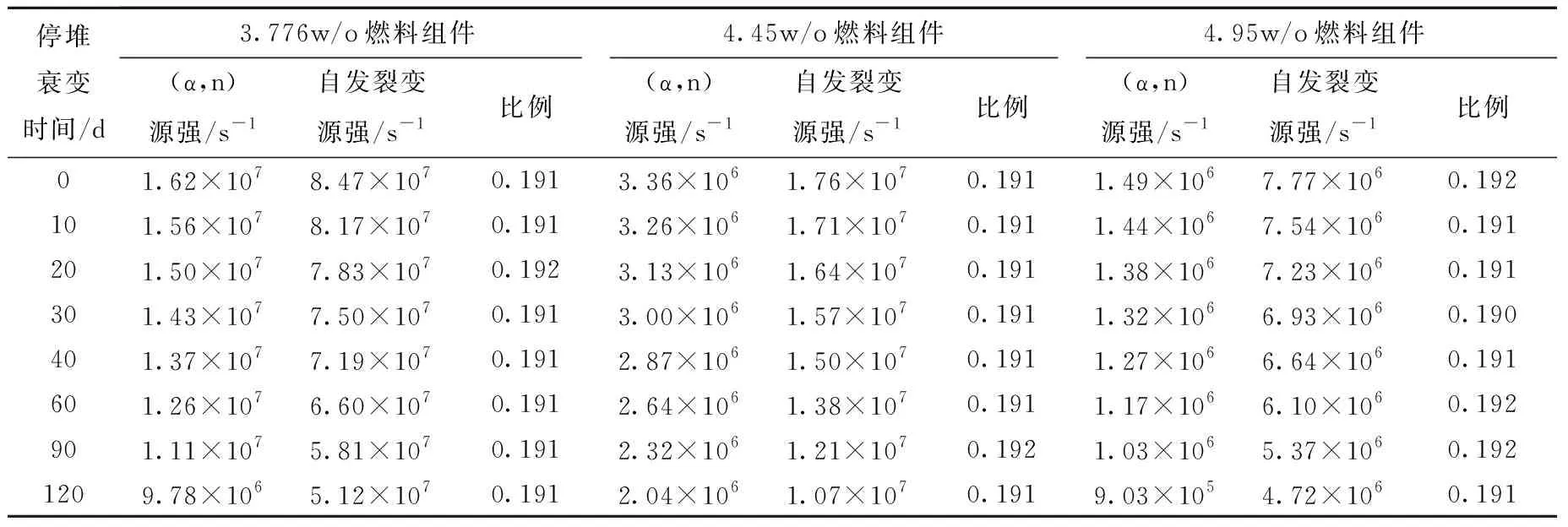
表2 不同富集度组件不同停堆衰变时间下242Cm的(α,n)源强占自发裂变源强比例Table 2 Ratio of (α,n) to spontaneous fission neutron of 242Cm for different enrichment assemblies at different shutdown decay time

方法2为比例系数拟合法。该方法通过拟合各富集度燃料随燃耗变化的(α,n)源强占辐照后总中子源强比例关系式，在自发裂变源强基础上计算(α,n)源强贡献。由图1可知：1) 不同富集度燃料组件(α,n)源强占辐照后总中子源强比例存在一定差异；2) 大于20 000 MW·d/tU燃耗区间，(α,n)源强占辐照后总中子源强比例随燃耗近似呈线性关系。基于上述结论，本文针对不同富集度组件，在不等于20 000 MW·d/tU燃耗区间，采用两种不同的拟合关系式，获取(α,n)源强占辐照后总中子源强比例随燃耗深度的变化关系。其中，小于20 000 MW·d/tU燃耗区间采用多项式拟合关系式，大于20 000 MW·d/tU燃耗区间采用线性拟合关系式。

图2给出3.776w/o燃料组件(α,n)源强占辐照后总中子源强比例在小于和大于20 000 MW·d/tU燃耗区间关于燃耗的拟合曲线，分别采用四阶多项式拟合和线性拟合。类似地，图3、4分别给出4.45w/o燃料组件和4.95w/o燃料组件(α,n)源强占辐照后总中子源强比例系数关于燃耗的拟合曲线。以上3种不同富集度燃料组件(α,n)源强比例拟合关系式分别见式(5)～(7)。

(5)

(6)

(7)

式中：y为(α,n)源强占辐照后总中子源强比例；x为组件燃耗，MW·d/tU。

由图2～4拟合结果可知，小于20 000 MW·d/tU燃耗区间的多项式拟合精度较高，但大于20 000 MW·d/tU燃耗区间的线性拟合存在一定偏差。为进一步评估线性拟合的偏差，表3列出不同富集度组件的线性拟合偏差，偏差最大值-8.1%，出现在3.776w/o燃料组件的48 000 MW·d/tU，其余偏差基本在5%以内。考虑到48 000 MW·d/tU工况(α,n)源强占辐照后总中子源强比例约为5%，因此线性拟合对总源的偏差贡献为-0.4%。

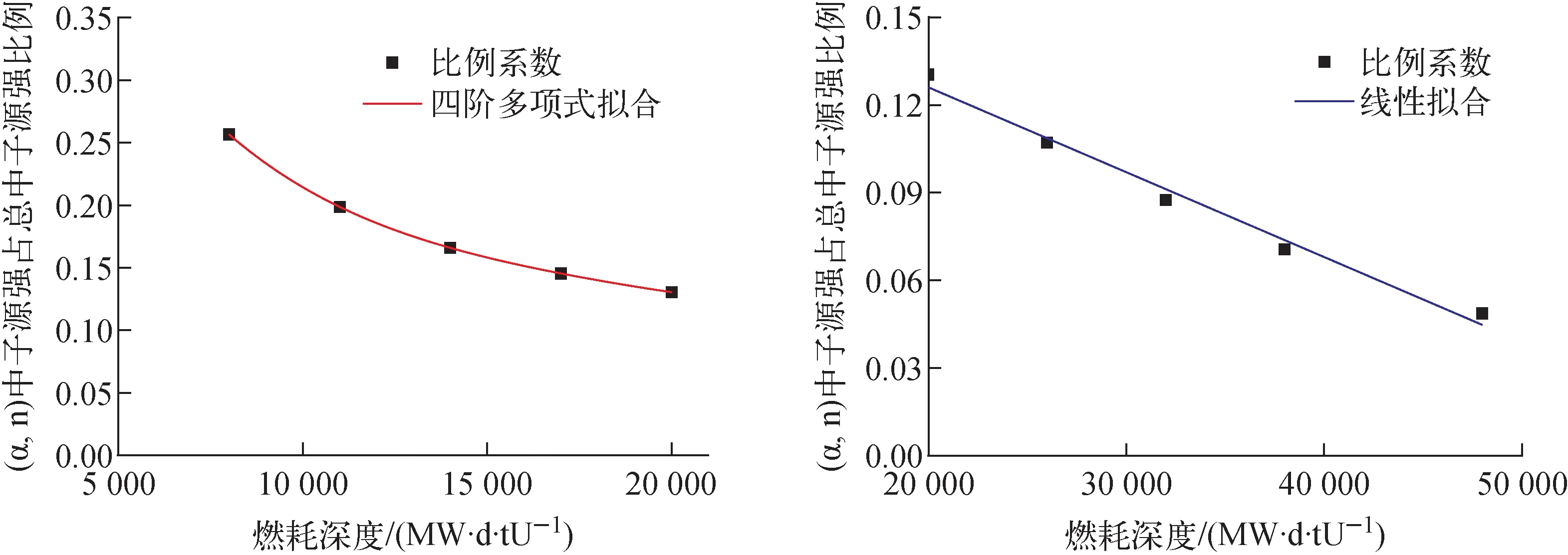
图2 3.776w/o燃料组件(α,n)源强占辐照后燃料总中子源强比例对燃耗的拟合Fig.2 Fitting for 3.776w/o fuel assembly ratio of (α,n) to total neutron about burnup

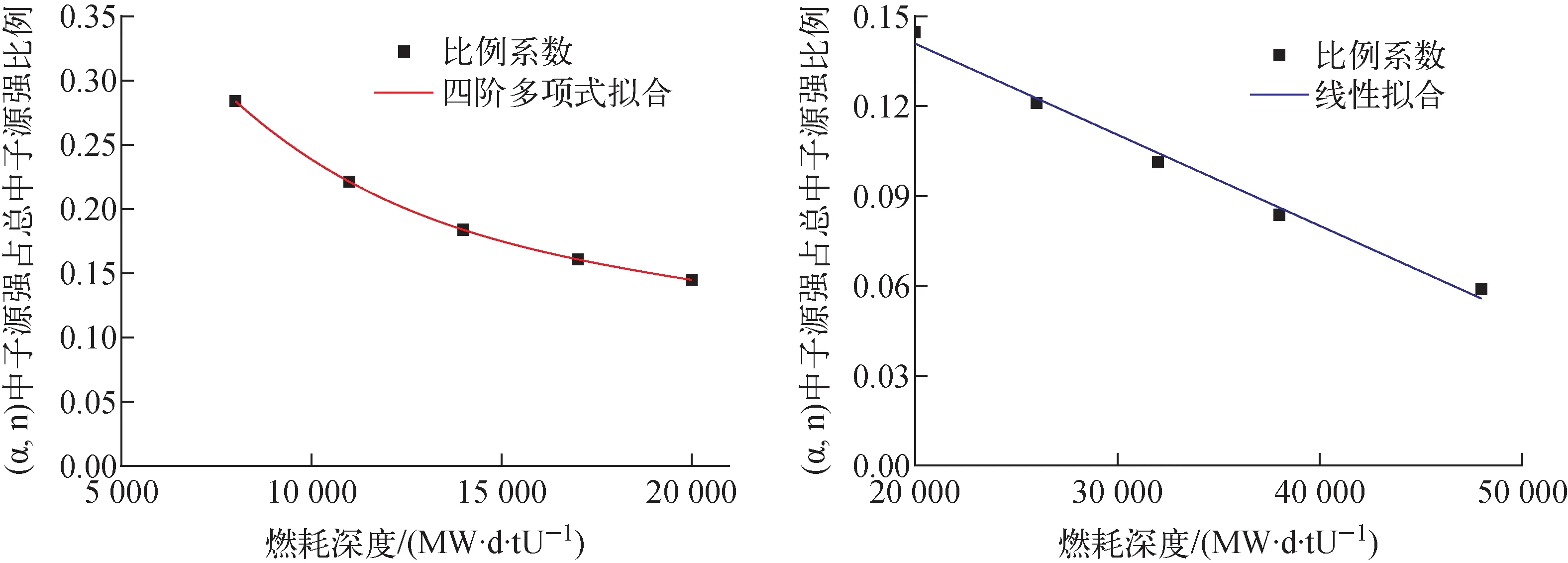
图3 4.45w/o燃料组件(α,n)源强占辐照后燃料总中子源强比例对燃耗的拟合Fig.3 Fitting for 4.45w/o fuel assembly ratio of (α,n) to total neutron about burnup

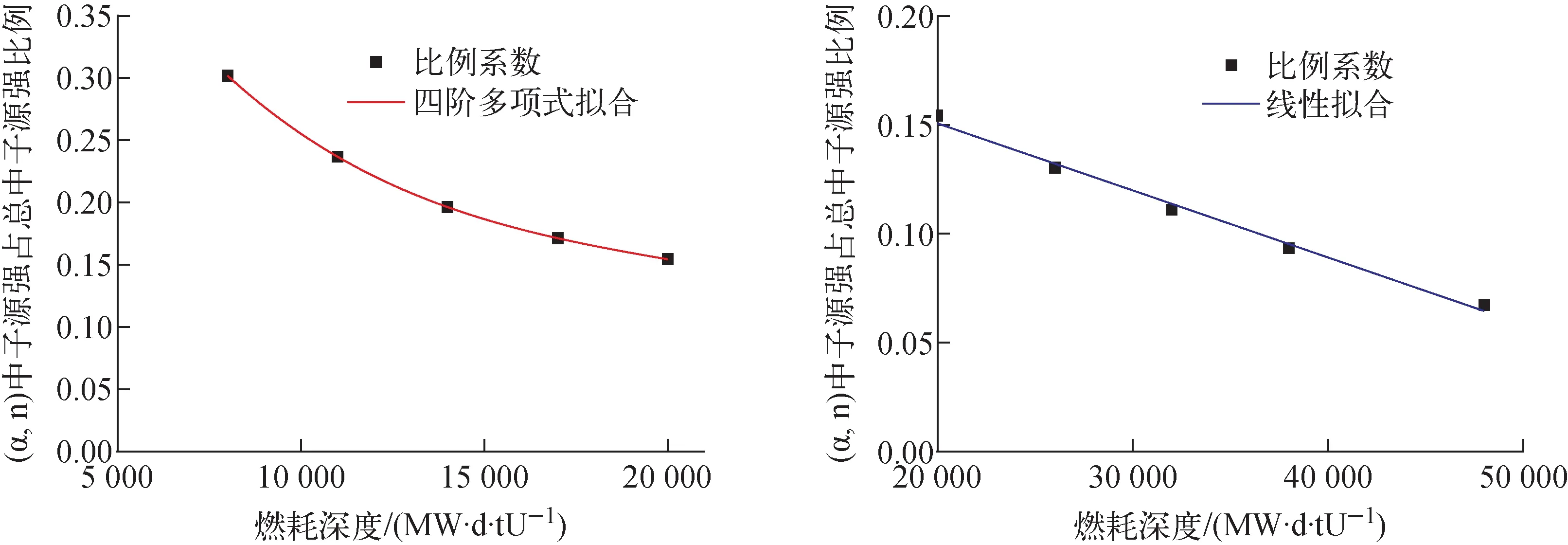
图4 4.95w/o燃料组件(α,n)源强占辐照后燃料总中子源强比例对燃耗的拟合Fig.4 Fitting for 4.95w/o fuel assembly ratio of (α,n) to total neutron about burnup

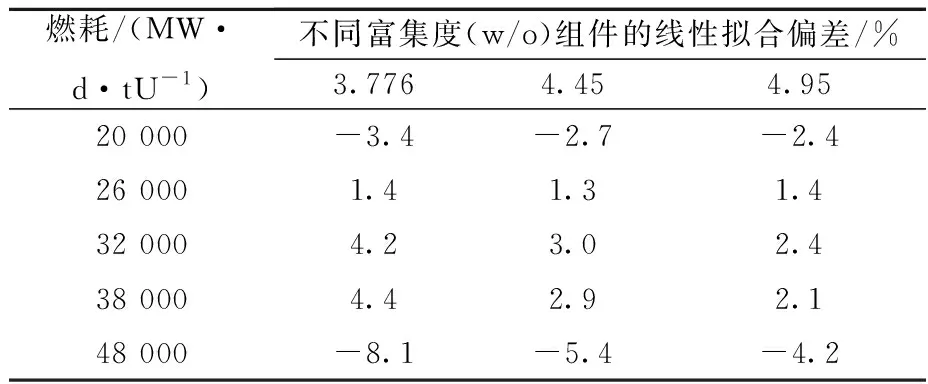
表3 不同富集度组件的线性拟合偏差Table 3 Deviation of linear fitting for different enrichment assemblies

2 数值结果

基于自主开发核设计程序系统，开发了压水堆辐照后燃料自发裂变源强和(α,n)源强计算模块。以某商用压水堆3.776w/o燃料组件为例，构造测试算例。分别使用ORIGEN程序和自主开发程序对该组件进行燃耗计算，对比分析了20 000 MW·d/tU和40 000 MW·d/tU燃耗点下的自发裂变源强、(α,n)源强和总源强计算结果。需指出，组件层面的自发裂变及(α,n)反应中子源强计算不涉及反应堆空间效应和实际运行历史效应，是给定燃耗历史的，ORIGEN程序针对给定燃耗历史计算结果是可靠的。因此，本文在燃料组件层面自发裂变及(α,n)反应中子源强的验证采用ORIGEN作为参考。

表4、5分别列出了各燃耗点下的自发裂变源强和(α,n)源强计算结果对比。由结果可知，对于自发裂变源强，与ORIGEN程序参考解相比，20 000 MW·d/tU和40 000 MW·d/tU下的最大相对偏差分别为-3.9%和-2.1%；对于(α,n)源强，与ORIGEN程序参考解相比，若采用242Cm近似法，各燃耗点下的最大相对偏差分别为-17.0%和-10.4%；若采用比例系数拟合法，则最大相对偏差分别为-6.6%和-7.4%。

表4 各燃耗点下的自发裂变源强计算结果对比Table 4 Comparison of spontaneous fission source intensity results

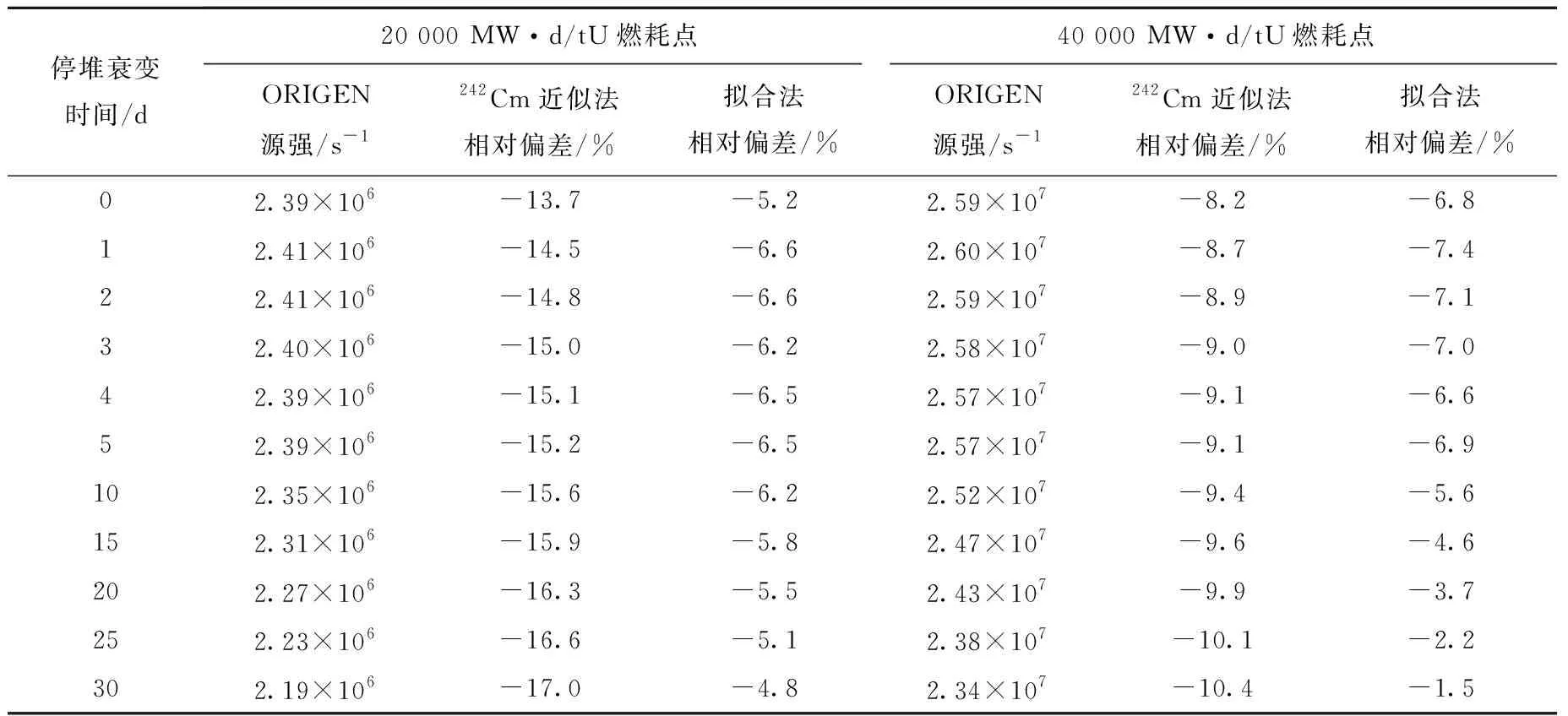
表5 各燃耗点下的(α,n)源强计算结果对比Table 5 Comparison of (α,n) neutron source intensity results

表6列出了各燃耗点下的总中子源强计算结果对比。由结果可知，若采用242Cm近似法，各燃耗点下的最大相对偏差分别为-5.5%和-2.5%；若采用比例系数拟合法，各燃耗点下总中子源强的最大相对偏差分别为-4.3%和-2.3%。

表6 各燃耗点下的总中子源强计算结果对比Table 6 Comparison of total neutron source intensity results

由以上的计算分析，可得到如下结论：1) 本文的自发裂变源强计算方法精度较高，最大相对偏差为-3.9%，但由于仅考虑了12种锕系核素的自发裂变(表1)，导致整体结果偏负；2) 基于比例系数拟合法的(α,n)源强计算方法，因考虑了更多核素的(α,n)反应，计算精度高于242Cm近似法。但由于(α,n)源强占总中子源强比例约13%，采用两种(α,n)源强计算方法得到的总中子源强精度相当，最大相对偏差约5%，因此两种(α,n)源强计算方法均具备工程应用价值。

考虑到242Cm近似法相对易于实施，在后续堆芯计算中推荐采用42Cm近似法计算(α,n)源强。在自主化堆芯计算程序中采用242Cm近似法计算(α,n)源强，计算得到典型压水堆临界前的堆芯三维辐照后燃料中子源强分布，详细考虑了反应堆空间效应和实际运行历史效应。将三维辐照后燃料中子源强分布分别在轴向和径向上归并，可得到辐照后燃料中子源强径向和轴向分布，如图5、6所示，图中同时给出了堆外源量程探测器径向和轴向位置示意。

图5 辐照后燃料中子源强径向分布(1/4堆芯)Fig.5 Radial distribution of burned fuel neutron source intensity (quarter core)

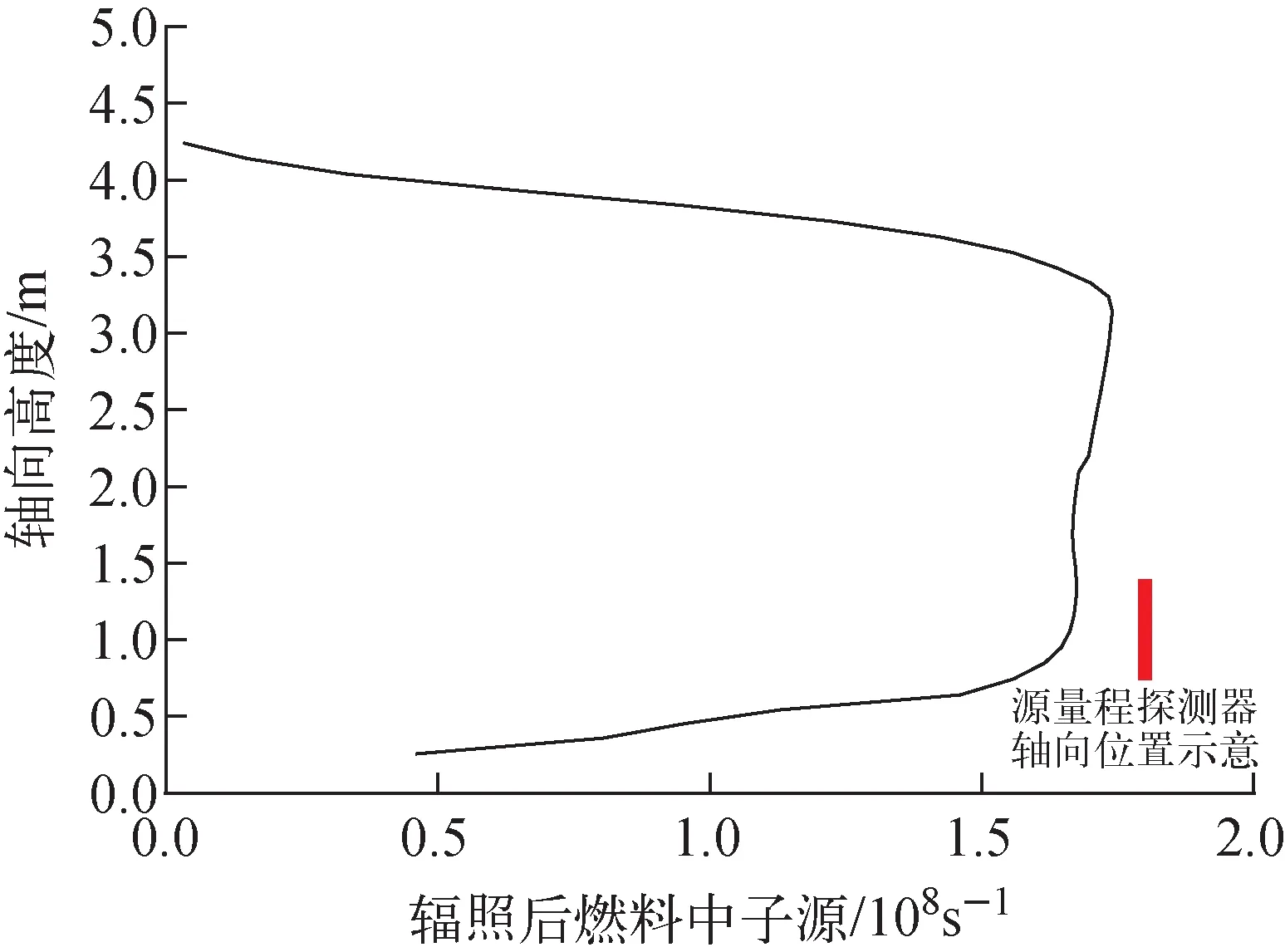
图6 辐照后燃料中子源强轴向分布Fig.6 Axial distribution of burned fuel neutron source intensity

3 结论

研究了在压水堆次临界状态下的堆芯反应性测量中具有重要作用的辐照后燃料中子源强，确定了辐照后燃料自发裂变源计算方法，提出了242Cm近似法和比例系数拟合法两种(α,n)源强计算方法，在自主研发堆芯核设计程序中开发了计算功能模块，考虑了反应堆空间效应和实际运行历史效应。组件层面的测试验证结果表明本文提出的辐照后燃料中子源强计算方法具有很高的计算精度，满足压水堆次临界状态下堆芯反应性测量时的源强计算需求。