内燃机机械主轴承损伤量化评估技术研究
李佳诚
(长春大学,松原 138000)
机械主轴承是现代内燃机机械的重要机械零件。机械主轴承经常处于高负荷和高转速等施工场景,因此对内燃机机械轴承进行实时定量评价是维护内燃机工作效能的关键。轴承处发生破损后,容易造成高频率同步振荡,严重时甚至产生高斯分布状态下的振荡。此外,随着凹槽的增大,轴承处造成的非规则振荡的能量波动随之增加[1]。目前,施工单位对机械轴承的故障评估技术不够全面,数据收集方法的自主程度较低,分解频带的模型状态混乱,无法量化评估轴承全过程的损伤情况,需要将具有主成分分析(Principal Component Analysis,PCA)特性的奇异值分解作为重构信号的基础数据。首先,选择恰当的嵌入维数和故障信号值,在保证信号稳定的前提下降低重构信号的故障频率。其次,使用具有自主性的自适应局部迭代滤波(Adaptive Local Iterative Filtering,ALIF)算法分解重构信号得到滤波函数。最后,将各阶段能量区间的JRD(Jensen-Renyi Divergence)值作为评估的量化指标,完成对轴承的损伤量化评估。
1 内燃机机械主轴承损伤量化评估技术
1.1 获取重构信号
对运行期间的内燃机机械主轴承进行检测时,脉冲和非规律的信号容易干扰轴承的振动,因此对检测方法的性能和稳定性提出了高要求。振动传感器在进行监测时,主轴承的旋转速度和情况不断改变[2]。为了使评估技术具有良好的适配性,要求可以非固定化地收集旋转主轴承的损伤信号。设从振动传感器采集的旋转主轴承损伤信号为X(t),离散化后为X=[x1,x2,…,xc],使用Tenkal矩阵空间进行轨迹X矩阵的重构,重构步骤可表示为

式中:μ为延迟时间;n为嵌入矩阵指数。这两项参数对主轴承损伤信号十分重要。确保轨道矩阵X的两个固定矢量的高度匹配,可以提高轨迹矩阵的复合线性。本文选择的延迟时间μ为1。嵌入矩阵指数n的选择由两个因素决定[3]。前者要求有较大的操作平台,后者则要求较小的嵌入矩阵指数,已获得更高的运算率。振动分析中,可将嵌入矩阵指数按所需的最小失效频率设置最低要求,形式为

式中:gq为取样频率;g为轴承理论失效次数。经数据分析,一般70%的组元能确保整个信号重建。
重构信号X´(t)可作为嵌入维数和故障频率的确定方法,用公式表示为

式中:s为固定参数;N为故障次数;v为X´(t)的极值。根据重构信号可以确定滤波器的长度,为滤波单元的设计提供数据基础。
1.2 设计滤波函数
重构信号后,需要对输入法框架(Input Method Framework,IMF)数量进行初始化。IMF为ALIF算法分解的n阶主轴承损坏信号,基于ALIF算法可以自动将其分解为n级失效信号。函数编程(Function Programming,FP)的加入使得算法在辨识随机故障信号方面具有良好的性能。FP有函数性能[4],且收敛性强。但是,由于非规则性的干扰,系统的收敛性随着信噪比的降低而降低,且ALIF算法在一定的迭代数内难以收敛。为了改善系统的信噪比,在输入AILF算法前应先设定一个预处理元件,以加快计算速率,降低迭代爆炸发生的概率。
为克服过多迭代和不确定性因素带来的影响,文章采用一种新的ALIF算法。该算法将带有主成分分析(Principal Component Analysis,PCA)特性的奇异值分解为ALIF的前置滤波器,并在此基础上对其进行预处理,然后利用同样数量的IMF进行运算。利用ALIF算法对内燃机机械主轴承信号的均衡滤波器进行改进,并将其应用于Fokker-Planck方程[5]。不仅可以减少信号干扰的次数,实现IMF的自主分解,还可以提高其滤波的精准度。假定h(a)和g(a)在(a,b)中符合光滑可导功能,则FP滤波器的特定表达方式为

基于g(a)<0 式(6)中需要判断X´(t)是否为所需项,也就是说其只有一个极值。若满足,则外层循环停止;如果不满足,则继续重复计算[6]。将以上步骤重复n次后,初始信号将会被分解为n阶故障频率IMF和一个x´(t)数值的总和,减少了迭代爆炸情况。 JRD能量熵能够细致表达频率间能量的微小变化[7]。JRD间距越大,损坏和未受损的内燃机机械主轴承差别越大,损伤程度越严重。本文定义损伤轴承与未损伤轴承的故障概率的能量分散程度,计算公式可表示为 式中:l为损伤轴承能量概率;l´为未损伤轴承的能量概率;a为参数变量;Dz为能量散度;i为IMF的阶段;n为ALIF的分解阶段。因此,能量分散程度的JRD距离可表示为 式中:DJRD为能量分散程度的JRD距离。它比较稳定和连续,同时具有更高的对称性。JRD距离可以反映轴承的损坏情况,从而可以对其损伤进行定量评价。 以轴承数据作为轴承故障的分析基础,故障信号来自系统的运行端振动信号,频率取值15 000 Hz。主轴承型号为4531—3TSJDMVKG,可进行全方位旋转。轴承的旋转体为10个,内圈直径为30 mm,外圈直径为60 mm,轴承厚度为20 mm,旋转体直径为8.23 mm,连接部位的直径为40.50 mm。轴承损伤部位的尺寸分别为0.022 70 mm、0.011 34 mm以及0.032 10 mm,损伤的类型为内圈、外圈和旋转体。该数据分别在运行阶段施加1HP、2HP以及3HP的负荷力,速度变化范围为1 843~1 856 r·s-1。在工程的轴承损伤阶段,本文选取3个数据集进行分析。工程概况的分类如表1所示。 表1 工况分类 在外圈故障的工况A下,采用JRD与内燃机机械主轴承损伤量化评估技术进行量化评估,各损伤阶段的量化评估结果如图1所示。 图1 两种技术的损伤量化对比 由图1可知,在相同数据集合中,内燃机机械主轴承损伤量化评估技术的变化幅度较小,说明在相同情况下的相同损伤部位,采用内燃机机械主轴承损伤量化评估技术得到的数据变化量小。在实际生产中,它可以准确评价旋转速度和负荷改变对定量评价的效果。同一条件下,不同抽样范围内的波动性计算公式可表示为 在3种工况下,传统评估方法和内燃机机械主轴承损伤量化评估技术的JRD值和波动率如表3所示。 根据表2可知,传统评估方法的JRD值有很大变动。JRD误差对主轴承失效损害的评价精度产生了一定影响,严重时可导致诊断错误,而内燃机机械主轴承损伤量化评估技术具有很好的稳定性。 表2 3种工况的JRD值波动率 本文提出了内燃机机械主轴承损伤的量化评估技术。通过研究发现,在相同数据集合中,内燃机机械主轴承损伤量化评估技术与传统评估技术相比变化的幅度较小,具有很好的稳定性。目前,内燃机机械主轴承损伤的量化评估技术尚处于发展阶段,距离实际目标尚有一定距离,需要进一步研究。
1.3 根据JRD距离数值进行评估
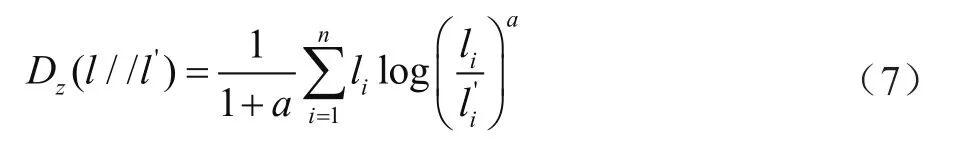
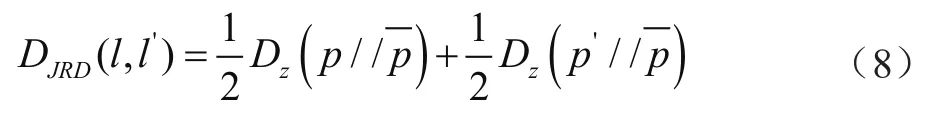
2 实验分析与结论




3 结语
——内燃机4.0 Highest Efficiency and Ultra Low Emission–Internal Combustion Engine 4.0

