基于自适应权值粒子群算法的滑动轴承优化设计

李 盼

（湖南城建职业技术学院，湘潭 411101）

电机是船舶推进系统的动力“心脏”。特别是在推进轴系中，由于大承载力的需求，很多电机主轴采用滑动轴承。相对于滚动轴承，滑动轴承具有承载能力大、抗振性能好以及价格低廉等优点，被广泛采用。在传统滑动轴承设计中，大部分采用的是经验设计。对于轴承的宽径比、轴承的相对间隙以及润滑油的动力黏度等设计参数的选择，常规的经验设计得到的结果往往不尽如人意。为了提高设计轴承的工作性能，可以采用智能优化算法对其进行多目标优化设计[1]。

本文选用的算法是自适应权值粒子群算法（Adaptive Partical Swarm Optimization，APSO）。相对于粒子群算法（Partical Swarm Optimization，PSO）[2]，APSO采用非线性动态权值系数，可以更好地解决PSO存在的局部极值、早熟收敛等问题，平衡PSO算法的全局搜索能力和局部改良能力[3]。本文以轴承宽径比、轴承相对间隙与润滑油动力黏度为设计参数，根据润滑特性计算得到的范围，采用合理约束条件，确立承载能力、轴承功耗以及轴承温升为目标函数，在分别进行单目标函数优化后，采用加权方法建立多目标函数模型进行优化设计[3]。将设计结果与常规设计结果进行对比分析，发现采用智能优化算法，轴承性能得到了显著提高，对轴承的结构设计具有很好的指导意义。

1 电机滑动轴承优化模型

图1为电机滑动轴承结构图。轴瓦部分采用推力瓦和径向瓦相结合的结构。因为该电机用于船舶推进系统，在工作过程中会在风浪的作用下短时间变成倾斜状态，所以需要考虑轴向力的作用。但是，该电机轴承在一般情况下主要受到径向力的作用，可以简化为径向滑动轴承模型。

图1 电机滑动轴承结构图

1.1 设计参数的确定

滑动轴承的设计参数中，对轴承性能影响较大的参数包括轴承宽径比、偏心率、润滑油的动力黏度。因此，选择的设计变量是轴承的宽径比B/d、轴承的相对间隙ψ以及润滑油的动力黏度η，即

式中：x1、x2、x3分别为3个设计变量。

1.2 目标函数的确定

为了保证轴承具有良好的工作性能，本文主要从3个方面考虑轴承的性能目标，即轴承的承载能力、轴承本身的功耗以及轴承的发热量[4]。

式中：f1(x)为承载力的倒数最小的目标函数；Cp为承载力系数；v为轴颈线速度；B/d为轴承的宽径比；d为轴径直径；F为轴承所受到的工作载荷；ψ为轴承的相对间隙；f2(x)为摩擦因数最小的目标函数；η为润滑油的动力黏度；ω为轴颈的角速度；p为轴承的比压；ξ为宽径比倒数的3/2次方；f3(x)为发热量最小的目标函数。

1.3 约束条件的确定

1.3.1 最小油膜厚度约束条件

根据流体润滑相关知识，为了保证轴承能够正常工作，必须要保证油膜厚度大于许用最小值，即

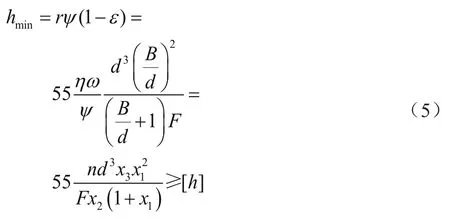
式中：hmin为油膜厚度的最小值；r为轴径半径；ε为轴承的偏心率；[h]为许用油膜厚度。

1.3.2 宽径比约束条件

根据设计准则[5]，轴承的宽径比需要满足以下条件

即

1.3.3 比压约束条件

比压约束条件为

式中：pmin为比压的最小值；pmax为比压的最大值；B为轴承的宽度。

即

1.3.4 相对间隙约束条件

相对间隙约束条件为

即

式中：ψmin为轴承相对间隙的最小值；ψmax为轴承相对间隙的最大值。

1.3.5 润滑油黏度约束条件

润滑油黏度约束条件为

式中：ηmin为润滑油动力黏度的最小值；ηmax为润滑油动力黏度的最大值。

1.3.6 温度约束条件

温度约束条件为

式中：ti为润滑油的入口温度，通常根据冷却装置的选择取为30～45 ℃；Δt为润滑油温度差。

2 电机滑动轴承优化算法

传统的设计方法主要采用的是经验设计，不仅耗时长、效率低，而且得到的设计结果有时候不尽如人意。为了使轴承获得更好的综合性能，本文采用一种群智能优化算法，即自适应权值粒子群算法（APSO），根据建立的相关数学模型优化设计轴承。

2.1 自适应权值粒子群算法

粒子群算法（PSO）[6]的主要思想是通过将微粒群的运动近似于鸟类的飞行，通过粒子群之间的协作与信息共享求解复杂的优化问题，即

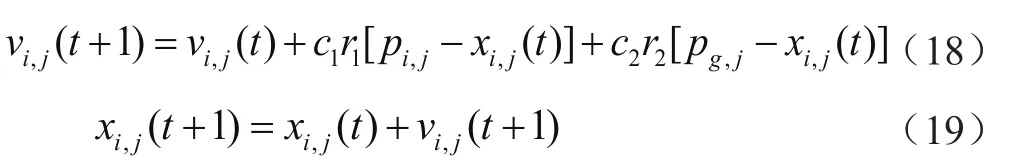
式中：vi,j(t+1)为t+1时刻微粒群的速度；vi,j(t)为t时刻微粒群的速度；c1和c2为非负常数的学习因子；r1和r1为相互独立的随机数，服从[0,1]上的均匀分布；pi,j为t时刻每个微粒所经过的最佳位置；pg,j为t时刻群体所发现的最佳位置；xi,j(t)为t时刻每个粒子的位置；xi,j(t+1)为t+1时刻每个粒子的位置。

为了更好地控制与调整微粒的飞行速度，引入惯性权重系数ω。同时，为了避免粒子群陷入局部极值、早熟等现象，平衡粒子群的局部改良能力与全局搜索能力，采用非线性动态惯性权值系数，称为自适应权值粒子群算法，即

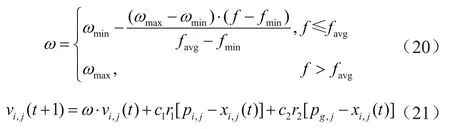
式中：ωmin为惯性权重系数的最小值；ωmax为惯性权重系数的最大值；f为微粒当前的目标函数值；fmin为当前所有微粒的最小目标值；favg为当前所有微粒的平均目标值。

2.2 外点惩罚函数法

轴承优化设计问题属于约束非线性规划问题，采用直接解法的难度大且难以得到良好结果。为了更好地求解该类问题，采用外点惩罚函数法[7]，即

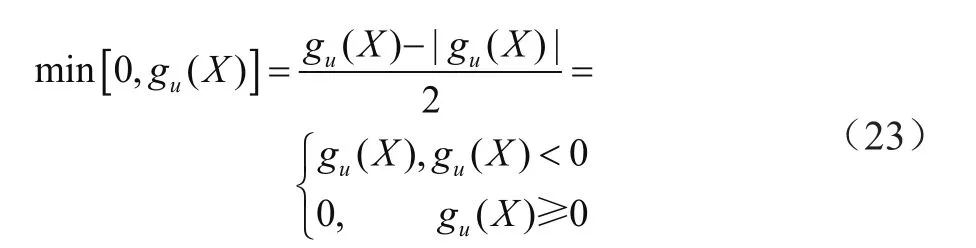
式 中 ：X为 设 计 变 量 ；γ(k)为 惩 罚 因 子 ；φ[X,γ(k)]为 惩 罚 函 数 形 式 ；f(X)为 原 目 标 函 数 ；为惩罚项；{min[0,gu(X)]}2为泛函形式；gu(X)为不等式约束条件。

3 电机滑动轴承优化结果

3.1 设计参数

通过分析得到电机轴承优化设计模型。本文采用Matlab软件编写计算程序，先计算单目标优化函数得到加权因子，再带入多目标优化函数计算得到轴承的性能。参数根据润滑特性计算获得，如表1所示。

表1 电机轴承优化设计参数表

3.2 单目标函数优化结果

图2～图7分别为各目标函数的优化结果和适应度曲线图。从优化结果和适应度图可知，自适应权值粒子群算法具有较好的鲁棒性和适应性，且均可得到优化的设计参数。

图2 承载力系数优化结果

图7 发热量为目标函数的适应度曲线图

3.3 多目标函数优化结果

将单目标函数优化结果的最优解即(0.519 3 0.001 6 1.309 0)代入加权因子计算公式可得加权因子，即(1.925 7,625,0.763 9)。

将加权因子带入多目标函数，可得

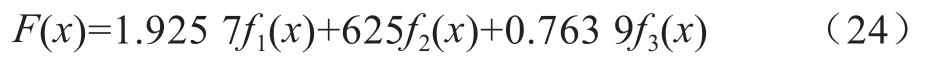
将式（24）作为目标函数，计算可得到多目标函数优化结果，如图8所示。

图8 多目标函数优化结果

图3 承载力系数为目标函数的适应度曲线图

图4 摩擦因数优化结果

图5 摩擦因数为目标函数的适应度曲线图

图6 发热量优化结果

从图9可知，自适应权值粒子群算法具有较好的鲁棒性和适应性。当X=[0.600 0 0.001 2 0.021 0]时，优化函数取得最优解，即2.718 8。

图9 多目标函数的适应度曲线图

采用对比法将优化后的数值进行处理，将其与之前通过经验设计得到的数值进行比较分析，可得到表2。其中：Cp为轴承的承载力系数；f为摩擦因数；pv为轴承的pv值，单位为MPa·m/s

从表2可知，采用APSO算法的优化设计，性能结果比经验设计得到的结果更好，承载能力提高了约13.20%，摩擦因数降低了约5.26%，发热量降低了约16.7%。该优化设计方法相比于常规设计方法，避免了经验设计存在的设计盲目性，对于后续轴承的设计特别是结构设计可以提供较好的指导作用。

表2 优化设计与常规设计结果对照表

4 结论

针对船用电机滑动轴承结构问题，选用自适应权值粒子群算法（APSO）进行优化设计，得出以下结论：

（1）常规的经验设计得到的结果往往不尽如人意，为了提高设计轴承的工作性能，需要采用智能优化算法（APSO）对其进行多目标优化设计；

（2）采用APSO算法的优化设计，其性能结果比常规设计得到的结果更好，即承载能力提高了13.20%，摩擦因数降低了5.26%，发热量降低了16.7%；

（3）智能优化算法相比于常规设计方法，避免了经验设计的盲目性，对轴承的结构设计具有良好的指导意义。