基于视觉感知的转杯混色纱颜色评价研究

杨月茹 夏宇航 蒋家淼 李玲利 吴艳丰 程 璐

（1.新疆大学，新疆乌鲁木齐， 830017；2.新疆溢达纺织有限公司，新疆乌鲁木齐， 841100）

色纺纱因其富有立体色彩感及风格多变等特点而拥有广阔消费市场前景，同时其具有“小批量，多品种，快交货”的市场需求［1］。然而，现阶段的色纺纱生产不仅配色过程复杂，且在对色过程的产品颜色评价阶段也存在不利于色纺纱企业扩展生产规模的问题，例如耗时长和对色人员受自身情绪等主观因素干扰导致评价不准确等。由此，将颜色评价的主观感知量客观定量化，即研究色差公式计算数值能否合适、准确地表征两个样品之间与人眼目测感觉相符的颜色差异跨度，可成为一种规避该类问题的可行性途径，以提高生产效率。

色差公式的提出是基于某一种均匀颜色样品进行大量颜色匹配试验研究而来，但在实际生产应用中对色差公式的使用是针对不同基底（纺织品、显示器图像、印刷体等）的颜色样本。因此，将不同色差计算公式应用到不同类别的颜色样品后会导致色差计算结果与人眼视觉感知呈现不同程度的不一致性［2］。本研究对象为色纺纱，其呈色机理复杂，与目前大多数研究所用颜色样本有着较大差异，因此对最为合适表征色纺纱颜色的色差公式研究具有重要意义。

目前在纺织领域直接以色差公式与人眼视觉特性一致性程度之间的矛盾点出发来对样品进行颜色评价的研究较少，但在印刷、图像等领域对主客观颜色评价相关研究较多。郭鹏飞等［3］基于光柱全息印刷品通过主客观评价研究得出CIELAB色差公式可较好地表征全息印刷品样本对之间的色差值；黄敏等［4］通过主观目测试验对7个色差公式表现性能进行对比，研究得出CAM02-SCD和CAM02-UCS色差公式的表现较好；汪哲弘［5］基于阴极射线管显示色检验CIELAB色度空间的色差公式，发现CIEDE2000表现最好；KIM D H等［6］选择染色涤纶织物，采用灰梯尺法主观评价得到CIE94色差方程的修正模型LCD公式的性能最好。

综上所述，针对3种色差计算公式，即最基础的CIELAB色差公式［7］、纺织行业常用的CMC（l∶c）色差公式［8］以及国际照明委员会（CIE）现推荐的CIEDE2000色差公式［9］，何者为最适用于以色纺纱为基底的颜色样本色差预测有待考究。为此，在本研究中纺制不同混色比例色纺纱颜色样本，设计人眼视觉评估试验，探究色纺纱视觉评估值与3个色差公式计算值主客观之间的相关性，确定适合本研究试验对象的色差公式。

1 颜色评价方法

1.1 主观评价

在纺织领域中进行主观评价色差时常采用灰卡评级的心理物理学试验方法。灰卡评级法是指借助灰色样卡中评价色牢度所用的级别来标定对色目测试验中有色标样与比样之间的颜色差异，且用于色差范围较广的色织物样品视觉色差评估［10-12］。本研究采用GB/T 250—2008《纺织品 色牢度试验 评定变色用灰色样卡》中的灰色样卡，该色卡共设置9对灰色对比色块，每对中的两个灰色色块之间的色差不同［13］。按照对比色块之间色差大小将色差划分为5级9档，色差由大至小分别对应色差级别1级到5级，且每两个整数级别之间存在一个半级［14］。在进行目测试验时，观察者依照规定要求观察标准光源下放置的标样与比样，通过感知两者之间的颜色差距并与灰卡中的级别进行比对，给出视觉感知的灰卡级别值。

1.2 客观评价

1.2.1CIELAB色差公式

CIELAB色差公式的提出为颜色科学领域的后续研究发展奠定了基础，其采用颜色空间中两个样品色度坐标点之间的几何距离表示，如式（1）所示。

式中：DL*为明度差异；Da*为偏红绿程度；Db*为偏黄蓝程度。

1.2.2CMC（l∶c）色差公式

CIELAB色差公式形式简洁，但其均匀性较差。当处于不同色区的两对样品应用该色差公式时，所计算得到的色差值相等，但人眼视觉反馈出的色差感知并不处于同一等级。为缓解此问题给实际生产应用带来的困扰，在CIELAB色差公式基础上，相关颜色研究工作者引入调整因子l和c及修正系数对公式进行优化，建立CMC（l∶c）色差公式，如式（2）所示。

式中：DL*、DC*、DH*分别为标样与比样的亮度差、饱和度差、色相差；SL、SC、SH为修正系数；l和c分别为调节明度和彩度的相对宽容量系数，纺织行业常采用l=2、c=1。

1.2.3CIEDE2000色差公式

色差公式不断加以修正、优化，2001年适用于中、小色差的CIEDE2000色差公式得到CIE推荐［15］，如式（3）所示。

式中：KL、KC和KH为与试验条件有关的校正系数，取KL∶KC∶KH=2∶1∶1；SL、SC及SH分别为明度、饱和度及色调的权重函数；RT为旋转函数，用来校正蓝色区域色分辨椭圆主轴方向的偏转。

1.3 色差评价效果统计方法

1.3.1性能评价因子PF/3

GUAN S等提出性能评价因子PF/3值作为表征两个数据集一致性程度的指标，如式（4）～式（9）所示，在分析主客观评价数据时多被采用［16］。PF/3数值越小，计算色差和人眼的目测数据之间的一致程度越高，即色差计算值更符合人眼对产品色差产生的感觉，色差公式的预测性能就越好。

式中：CV为变化量的系数；γ和VAB均表示两个对比数据集之间的不一致性程度；N为颜色刺激色样数据组的个数；ΔEi和ΔVi分别为第i对样品对的色差计算值和视觉感知量；F、f为系数因子。

1.3.2标准化残差平方和STRESS

与PF/3近似，STRESS的数值越小，表明计算色差和人眼目测数据之间的一致程度越高，其取值范围是0～100。STRESS的计算公式如式（10）所示。

2 试验与结果

2.1 制样及颜色测量

2.1.1样品原料选取

根据颜色视觉理论，某一种颜色可由红、黄、蓝三原色不同比例混合而成，混成颜色可占据色域空间较大的区域，是较为全面且常用的原色体系。本研究选用由博拉经纬纤维有限公司提供的红、黄、蓝3种原液着色粘胶散纤维作为试验原料，平均纤维长度33.2 mm，线密度1.95 dtex，散纤维实物图如图1所示，其色度参数见表1。

图1 散纤维实物图

表1 单色纤维色度参数值

2.1.2颜色样本对选择

本研究共设置53个混配比例，采用转杯纺纱方式纺制颜色样品。具体纺纱工艺流程：称量纤维（FA124型电子天平）→手扯开松→FB360型梳理打样机（梳理三次）→A301型并条试验机（三道）→FA601A型转杯纺纱试验机。为控制混配比例单一变量，避免其他因素的干扰，在制备试验样本时将纱线线密度固定为58.3 tex，且手工紧密绕制纱线色卡便于后续颜色测量。部分色纺纱样品纺制实例如图2所示。

试验者首先通过目测评估筛选颜色接近、颜色差异较小的色样，组成人眼主观评价色差试验所用颜色样本对54对，3种单色纤维混配质量比例总递增减量基本控制在0～20%之间。颜色样本对配对设置见表2。

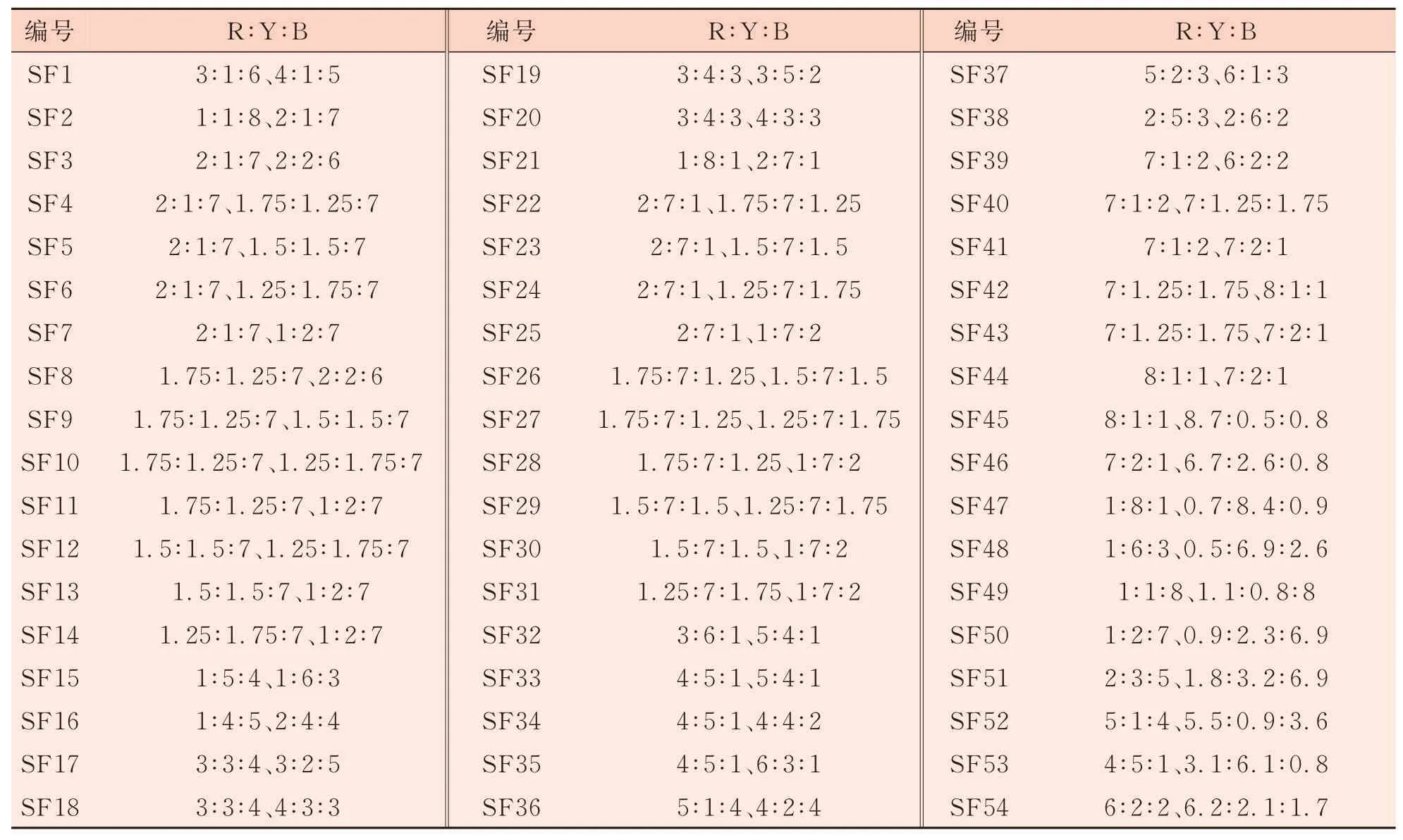
表2 颜色样本对设置

2.1.3色度学指标测量

采用上海韵鼎国际贸易有限公司提供的Hunter Lab Ultra Scan PRO测色仪测量试验样本的光谱反射率值。仪器参数设定：光线几何条件确定为照明观察条件d/8、照明光源D65、测量孔径0.991 cm，在光阱和白板的校准完成后进行试验。将绕制色纱样卡的正面（缠绕的纱线整齐度好的一面）对准测试孔径，选取不同的6个测样点进行测试，取平均值。

2.2 人眼视觉评价试验

本研究选择经过石原氏色盲测验后色觉正常的观察者20人，测试环境尽量保持黑暗，观察者观测条件参考AATCC评定程序9《纺织品色差的目视评定》。试验者向观察者介绍试验内容，将本试验目测色差评定参数设置准则告知观察者，以变色用灰色样卡作为察觉颜色差异的参考对，将试验色样对与之对比，确认试验样对之间的观感色差接近于灰卡某级别所具有的观感色差时，记录该级数作为该试验样对的目测结果Gi值（1、2、3、4），中间等级按0.5来记录。将每次判断的结果Gi取平均值，获得观察者评估的最终结果。

2.3 主客观色差测量值计算

运用MATLAB软件，将筛选的54对样品对的反射率代入色差公式，分别计算得CIELAB、CMC（l∶c）、CIEDE2000共3种不同色差公式的色差处理结果ΔE。将其整理至EXCEL表格。同时将目测评估试验得到的灰卡级别G值对应记录，使用MATLAB软件将两组数据进行多项式拟合，G值代入关系式即得视觉感知量ΔV，此数值将用于PF/3及STRESS指标的计算。

2.4 观察者准确性

2.4.1误判率

本研究评价观察者的准确性采用误判率（WD），WD的取值范围是0～100%，WD的值越接近于0，则说明观察者在此次试验的判断越精准。计算公式如式（11）所示。

式中：N为总样品对数量；Wi为与错误判断次数占总判断次数的比例。

在本研究中以每对样品对的灰卡级别均值为基准，观察评级结果大于均值的观察次数超过半数时，认为大于均值的级别为正确决定，小于均值的评级结果则为错误判断，反之亦然。每对样品共被20人观察，每人观察3次，一对样品共被观察60次。计算每一对样品对大于、小于均值的次数，在认定正确决定的前提下计算每一位观察者做出与整体评估情况不同的观察次数，将其除以总观察次数3，即得每位观察者对某一样品对的观察结果误判率。最后将20人次观察的54对样品对的误判率作平均处理，此平均值即可作为观察者的准确性，观察者准确性结果见表3。

表3 观察者的准确性

数据处理结果显示，20人次观察中误判率最大为50.10%，最小为13.30%，均值为35.40%。与多位前人的研究数据比较，除去观察者15和观察者18，本试验其他观察者数据均在可接受的范围内，因此本研究中的人眼目测评价色差试验数据是具有有效性的［17-18］。

2.4.2反射率偏差

反射率偏差是标样反射率与比样反射率之差的绝对值除以标样的数值，可以反映两个色样之间的颜色差异，反射率偏差值越小，表明两者的颜色越相近。本研究引入反射率偏差与灰卡级别G值对比作为观察者准确性的评价指标，结果见表4。

表4 颜色样本对反射率偏差

通过Minitab对表4两组数据作异常值分析后再进行相关系数分析。相关系数为-0.445，呈现一般的负相关性，p值为0.001，小于显著性水平α=0.05，否定了原假设p＞0.05时无显著线性相关性，即可认为反射率偏差与G值为负相关。两者整体呈现反射率偏差越小，灰卡级别G值越大；G值越大，样品对给人的视觉感知差异越小，由此也可验证本研究目测评价结果较为准确。

2.5 色差公式评价效果分析

将获得的色差计算值与经过数据处理后的视觉感知量整理于EXCEL表格中，将CIELAB、CMC（2∶1）、CIEDE2000色差公式计算的样品对色差数值分别于各自拟合得到的视觉感知量代入PF/3以及STRESS公式，对两两配对，共3组的数列数据进行计算处理。PF/3及STRESS两项评价指标均数值越小，公式的预测性能越好。CIELAB、CMC（2∶1）、CIEDE2000色差公式的PF/3分别为22.33、19.02、41.24。结果显示，针对原液着色粘胶纤维转杯纱，CMC（2∶1）色差公式的预测性能最优，即人眼目测感觉与色差计算结果符合程度是最好的，相同的数值变化给人不同的颜色差别感觉较小；CIELAB次之，CIEDE2000最 差。CIELAB、CMC（2∶1）、CIEDE2000色差公式的STRESS分别为28.78、24.72、40.47。借助STRESS评价方式所得的结果与PF/3保持一致。为将色差公式预测性能发挥至最优，后续仍需更多的颜色科学工作者创建不同材料的色差数据集来研究不同色差公式所对应的最合适应用对象。

3 结论

本课题主要研究了3种色差公式对原液着色粘胶纤维转杯纱色差的预测性能，探究最适合表征色纺纱颜色差异的色差公式，得到以下结论。

（1）在进行观察者准确性分析中，其均值为35.40%。与前人研究数据以及反射率偏差结果相比较，本次视觉评价试验数据是有效的。

（2）计算样本对的反射率偏差，其也可表征样本对的颜色差异，同时可以检验目测试验评价的效果，两者整体反映出一致的规律，即反射率偏差越小，灰卡级别G值越大，两样本之间的颜色差异越小。

（3）在以本试验设置混纺比例的色纺纱为研究对象来探究3种色差公式与人眼目测一致性程度试验中，CMC（2∶1）、CIELAB、CIEDE2000的PF/3和STRESS值分别为19.02、22.33、41.24和24.72、28.78、40.47。CMC（2∶1）预测性能最优，CIELAB次之，CIEDE2000最差。因研究对象的不同且色纺纱呈色机理较为复杂，CIEDE2000的预测性能表现不好，与前人应用此方法的研究结论有所出入，故此问题需继续加以研究。