基于改进粒子群算法的储能调峰容量优化配置研究

刘红

(南方电网广东东莞供电局，广东 东莞 523000)

近年来，减少碳排放已成为世界各国的重要战略共识。中国积极践行生态优先、绿色低碳的发展道路，大力发展风电、光伏等清洁可再生能源。根据《中国电力行业年度发展报告2021》，截止到2020年年底，并网风电281.65 GW，比上年增长34.7%；并网太阳能发电253.56 GW，比上年增长24.1%[1]。然而，由于风电、光伏等清洁能源发电具有间断性、波动性、随机性等不友好特性，其大规模并网影响了电网的稳定性、安全性和可靠性[2]。

为了实现“双碳”目标，我国将持续增加光伏、风电等清洁能源装机，加快清洁能源发电并网，这给电网带来了更加严峻的挑战，其中调峰问题尤为显著[3]。在这一背景下，储能由于具有容量大、灵活性强、效率高等优点，可以提供调频、调峰、调压等辅助服务，解决清洁能源并网带来的一系列问题，越来越受到人们的重视与关注。而且随着储能技术的成熟，储能成本逐渐下降，储能的竞争性不断增强。因此，探究储能调峰容量的优化配置尤为必要。

目前，诸多学者探究了储能调峰的容量优化配置。文献[4]提出了考虑储能综合系统运行成本和储能投资成本的储能选址和容量优化的双层模型。文献[5]从技术和经济角度出发，提出一种储能辅助电网调峰的配置方案。文献[6]基于调峰成本最小目标，提出了多类型电源参与调峰辅助服务市场模型。文献[7]考虑火电深度调峰，针对多类型储能系统的经济性进行分析。文献[8]提出计及循环寿命的储能配置与运营两阶段优化策略。文献[9]考虑风电的反调峰特性，提出了储能调峰优化策略。文献[10]提出了考虑电氢耦合的风光场站氢储能优化配置策略。

虽然上述文献对储能调峰的优化配置进行了研究，但大多未同时考虑经济性和调峰效果。有些文献虽然同时考虑了两者，但是仅仅将2个目标标准化后简单相加转化为单目标求解，所得结果未考虑2个目标的重要性程度差异。此外，这些文献多是根据单个典型日负荷曲线进行储能容量的优化配置，没有考虑不同季节典型日间的差异。这样配置的储能无法保证配置结果的准确性。基于此，本文以工业园区为研究对象，在分析储能调峰机理的基础上，综合考虑储能系统的充放电损耗、峰谷差率、成本、收益等多方面因素，以储能调峰效果为约束条件，以经济性为目标，构建储能调峰容量优化配置模型，并综合考虑不同储能系统、不同季节典型日的差异，探究工业园区中储能参与调峰的容量优化配置。

1 储能调峰机理分析

由于储能系统具有能量转移的时空特性，可以通过充放电过程参与电网调峰，其参与调峰的机理如图1所示，图1中：Pmax为调峰前负荷的峰值，Pmin为调峰前负荷的谷值，ΔP1为调峰前负荷的峰谷差，P1为削峰线，P2为填谷线，ΔP2为调峰后负荷的峰谷差，Pcmin、Pcmax分别为常规能源的最小出力和最大出力。当负荷低于P2时，储能系统进行充电；当负荷高于P1时，储能系统进行放电；当负荷介于两者之间时，其他常规能源和新能源出力能满足实际需求，储能系统既不充电也不放电。通过此种方式，降低了负荷的峰谷差值，从而达到削峰填谷的效果。

图1 储能调峰机理示意图Fig.1 Schematic diagram of energy storage peak regulation mechanism

2 储能调峰日效益模型

储能系统调峰的收益主要包含低储高发套利收益、调峰补偿收益、环境收益、新增新能源消纳量收益等部分，具体可表示为

I=I1+I2+I3+I4.

(1)

式中：I为储能调峰的日收益，元；I1为低储高发套利收益，元；I2为调峰补偿收益，元；I3为环境收益，元；I4为新增新能源消纳量收益，元。

2.1 储能低储高发套利收益

储能的低储高发套利收益为储能系统在低负荷时充电在高负荷时放电由于峰谷价差所获得的收益，表示为

(2)

式中：ac、af分别为储能系统的充、放电效率；Pc(t)、Pf(t)分别为t时刻储能系统中储能设备从电网充、放电的功率(简称储能充、放电功率，下同)，kW；Cf、Cg分别为调度日当日的峰、谷电价,元/kWh。

2.2 储能调峰补偿收益

储能调峰补偿收益为储能系统参与调峰时根据各地方政策给予的补偿。参考文献[5]的处理方式，I2可表示为

(3)

式中pa为单位电量调峰补偿价格，元/kWh。

2.3 储能调峰环境收益

储能调峰环境收益为储能系统替代火电等其他调峰方式减少污染物排放所带来的环境收益。主要表现为储能系统向电网放电时，替代了其他调峰方式向电网供电，减少了一部分污染物排放，增加了环境收益。因此，参考文献[11]的处理方式，I3可表示为

(4)

式中pb为单位电量增加的环境价值，元/kWh。

2.4 储能新增新能源消纳量收益

储能新增新能源消纳量收益为当新能源出力呈反调峰特性[12]时，在负荷低谷时，储能系统参与调峰所增加新能源消纳量(即减少弃风弃光量)带来的收益，参考文献[5]，I4可表示为

(5)

式中pc为单位弃风弃光惩罚价格。

3 储能日成本模型

在分析储能系统的经济性时，除要考虑储能参与调峰所获得的效益外，还要分析其成本。在分析储能系统的成本时，主要需要考虑储能系统的建设成本、运维成本及设备残值等方面，因此，储能系统的总成本

C=C1+C2-C3.

(6)

式中：C1为储能系统的日建设成本，元；C2为储能系统的日运行维护成本，元；C3为储能系统的日设备残值，元。

3.1 储能建设成本

储能系统的建设成本主要包含功率成本和容量成本2部分。其中，功率成本由储能系统的额定功率决定，容量成本由其额定容量决定[13]。考虑到储能系统的全生命周期，则储能系统的日建设成本

C1=r(1+r)m(CPPP+CSES)/365[(1+r)m-1].

(7)

式中：r为基准折现率；m为储能系统的寿命，年；CP为储能系统的单位功率成本，元/kW；CS为储能系统的单位容量成本，元/kWh；PP为储能系统的额定功率，kW；ES为储能系统的额定容量，kWh。

3.2 储能运维成本

储能系统的运维成本主要由固定运维成本和可变运维成本2部分组成。其中，固定运维成本与储能系统的额定功率有关，可变运维成本与储能的充放电量有关[14]。因此，储能日运维成本

(8)

式中：CPW为储能系统单位功率的年固定运维成本，元/年；CSW为储能系统单位容量的可变运维成本，元/kWh。

3.3 储能设备残值

储能设备残值是指储能系统内的设备在报废后其中的贵金属等可被回收利用部分的价值。假定储能设备残值与其建设和运维成本之和呈线性关系，则储能设备残值

C3=a(C1+C2).

(9)

式中a为储能设备残值系数。

4 储能调峰容量优化配置

4.1 目标函数

综合上文分析，考虑储能调峰的成本、收益等经济性因素，以日净收益fI-C最大为目标函数建立储能调峰容量优化配置模型，如式(10)所示。

maxfI-C=(I1+I2+I3+I4)-(C1+C2-C3).

(10)

4.2 约束条件

a)储能功率约束。储能功率约束指储能系统中储能设备的实际充放电功率不大于其额定功率，且不能同时进行充放电过程，见式(11)—(13)。

0≤Pc(t)≤PP,

(11)

0≤Pf(t)≤PP,

(12)

Pc(t)Pf(t)=0.

(13)

b)储能荷电状态约束。储能荷电状态约束指为保证储能系统长期稳定运行，储能系统参与调峰的过程中，将储能系统的实时容量与额定容量的比值限制在一定范围内，如下：

(14)

式中：Et为t时刻储能系统的容量，kWh；Smax、Smin分别为荷电状态上下限。

c)峰谷差率约束。峰谷差率约束是指事先约定好的储能系统参与调峰的调峰效果约束。

b=(P1-P2)/P1≤K1.

(15)

式中：b为储能调峰后的峰谷差率；P1、P2分别为储能参与调峰后的最大负荷、最小负荷，kW，见式(16)—(18)；K1为峰谷差率上限。

P′(t)=P(t)+Pc(t)/ac-Pf(t)af,

(16)

P1=max(P′(t)),

(17)

P2=min(P′(t)).

(18)

式(16)中P(t)、P′(t)分别为t时刻储能参与调峰前、后电网的净负荷，且

(19)

式中：Pi为第i种清洁能源出力；P0(t)为t时刻储能参与调峰前电网的负荷；k为清洁能源种类数。

d)储能容量平衡约束。储能容量平衡约束是指在单个调度日内储能系统的初始状态和结束状态相同，即

(20)

式中T为单个调度日的总时段数。

(5)系统功率平衡约束。系统功率平衡约束指任意时刻系统内不同清洁能源出力、净负荷与储能充放电功率之和等于调峰前t时刻电网的负荷，即

(21)

4.3 求解方法

标准粒子群算法是一种模拟鸟群群体觅食活动而发展起来的智能算法。该算法的实质是在模拟鸟群在寻找食物的过程中，基于共享信息的理念，鸟群中的每个个体可以根据种群最佳位置和个体最佳位置来改变自己的位置，从而更快速地找到目标食物[15]。将鸟群中的每个个体作为单个粒子，则其速度和位置更新过程可用式(22)、(23)表示。

vj+1=wvj+c1(g-xj)R+c2(z-xj)R,

(22)

xj+1=xj+vj+1.

(23)

式中：vj+1、xj+1分别为粒子下一次速度和位置，vj、xj分别为粒子当前速度和位置；R为随机函数；g为粒子种群的最佳位置；z为该粒子的最佳位置；w为惯性权重；c1、c2为学习因子。

标准粒子群算法相较于其他智能算法具有计算速度快、易收敛等优点，但同时存在一定缺陷。惯性权重和学习因子是标准粒子群优化算法中控制迭代寻优步长的关键因素，由于两者是定值，如果步长过大，可能找不到最优解；如果步长过小，可能陷入局部最优，也可能导致收敛速度过慢。为了避免此种结果，本文采用线性递减的惯性权重[16]和异步学习的学习因子[17]对标准粒子群优化算法进行改进，使其能在加快算法收敛速度的同时避免陷入局部最优，见式(24)—(26)。

w=wmax-(wmax-wmin)j/n,

(24)

c1=c1st+(c1en-c1st)j/n,

(25)

c2=c2st+(c2en-c2st)j/n.

(26)

式(24)—(26)中：wmax、wmin分别为惯性权重w的最大值与最小值；c1st、c1en分别为学习因子c1的初始值、结束值；c2st、c2en分别为学习因子c2的初始值、结束值；j为当前迭代次数；n为最大迭代次数。

本文基于提出的改进粒子群算法，采用MATLAB 2021a软件编写程序进行求解，从而实现储能调峰容量优化配置。其流程如图2所示，具体详细步骤如下：

图2 储能调峰容量优化配置流程Fig.2 Flow chart of energy storage peak regulation capacity optimization configuration

a)初始化相关数据。根据电网的实际运行情况，初始化负荷、储能系统相关参数及电价等相关数据。

b)初始化种群。根据种群大小，随机生成不同的削峰线，从而对种群进行初始化，并设置最大迭代次数等相关参数。

c)计算目标函数值。根据不同的削峰线，考虑储能容量平衡、调峰后峰谷差率约束、荷电状态约束、功率约束等，计算得出对应的最佳填谷线和此时的最大日净收益，即目标函数值。

d)根据目标函数值，确定粒子最优解及全局最优解。

e)更新粒子的速度和位置。根据粒子最优解和全局最优解，更新粒子的速度和位置，计算此时粒子对应的目标函数值，并与上一次粒子目标函数值进行比较，取较大者为粒子最优解，并更新粒子全局最优解。

f)重复迭代直至最大迭代次数。若收敛，则输出粒子全局最优解及对应的最佳填谷线；否则继续迭代。

g)计算储能容量优化配置结果。根据最终的粒子全局最优解及对应的最佳填谷线，结合储能荷电状态、功率等约束，计算得出对应的储能功率和容量，即为储能系统应配置的最佳功率和容量。

5 实证分析

5.1 算例设置

5.1.1 算例目的

拟实现对L地区M工业园区(下称M园区)的储能容量进行优化配置。M园区日平均负荷约1 500 MW，配备了350 MW的风电发电机组。假定该工业园区仅使用储能系统进行调峰，且储能系统仅用于调峰。

5.1.2 求解思路

a)不同季节M园区储能容量优化配置。根据不同季节典型日净负荷曲线，考虑不同电池储能系统差异，使用所提策略和方法，分别进行储能容量优化配置。

b)M园区储能容量优化配置。以典型负荷曲线中对储能需求最大的场景作为规划依据，确定M园区储能系统容量优化配置结果。

5.1.3 算例参数

a)仿真数据。参考文献[18]的相关数据，对该工业园区不同季节典型日的负荷、新能源出力数据进行模拟预测，并由此计算出该工业园区不同季节典型日的净负荷。M园区不同季节典型日净负荷曲线如图3所示。

图3 M园区不同季节典型日净负荷曲线Fig.3 Net load curves on typical days in different seasons in M park

从图3可以看出，不同季节典型日净负荷曲线间存在较大差异，因此需要先针对不同季节特点分别进行储能容量优化配置，再以典型负荷曲线中对储能需求最大的场景作为规划依据，确定M园区储能系统容量优化配置结果。

b)储能系统参数。假定M园区拟采用电池储能系统进行调峰，参考文献[19-22]，不同电池储能系统的相关参数见表1。

表1 电池储能系统参数Tab.1 Parameters of battery energy storage system

c)L地区分时电价表。假定L地区电费采用分时定价的方式进行计价，不同时刻的电价见表2[23]。

表2 L地区分时电价表Tab.2 Time-of-use electricity price in L area

d)其他数据设定。假定L地区调峰补偿价格为0.2元/kWh，弃风弃光惩罚价格为0.15元/kWh[5,11]，单位电量增加的环境价值为0.14元/kWh[7,24]，调峰后的峰谷差率不大于0.35，基准折现率为5%，储能设备残值系数为0.05[14]。

5.2 结果分析

5.2.1 改进粒子群算法有效性验证

为了验证上述所提改进粒子群方法的有效性，本文首先选择铅炭电池作为储能系统对M园区进行调峰，分别使用标准粒子群算法和改进粒子群算法对储能系统的容量进行优化配置。其中，标准粒子群算法的惯性权重w为1，学习因子c1、c2均为1.5。改进粒子群算法的惯性权重最大值为0.9，最小值为0.4；学习因子c1的初始值和结束值分别为0.5、2.5；学习因子c2的初始值和结束值分别为2.5、0.5。2种算法的种群规模均为300，最大迭代次数均为400。以夏季储能容量优化配置为例，2种算法的迭代过程对比如图4所示。

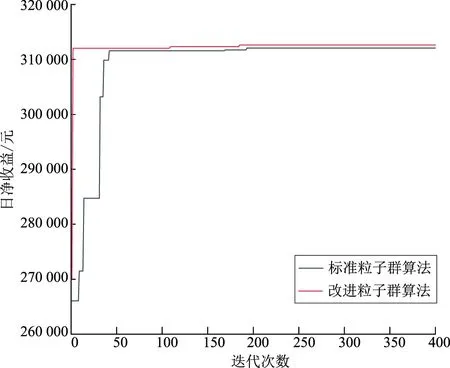
图4 改进粒子群算法与标准粒子群算法日净收益计算迭代对比Fig.4 Iterative comparisons of improved particle swarm and standard particle swarm optimization algorithms for daily net gain calculation

从图4可以看出，改进粒子群算法的收敛速度较标准粒子群算法快，两者所得到的日净收益很基本相同，且改进粒子群算法略大些，这说明改进粒子群算法在接近收敛时局部搜索范围更大。综上，证明了本文提出的改进粒子群算法的有效性。

5.2.2 铅炭电池储能系统调峰结果分析

使用改进粒子群算法对铅炭电池储能系统调峰容量进行优化配置。以夏季储能容量优化配置为例，在满足预期调峰效果、储能系统容量平衡等多项约束限制下，经多次迭代，当储能系统日净收益最大时，储能系统调峰前后的净负荷曲线如图5所示，储能系统的实时功率及荷电状态如图6所示。

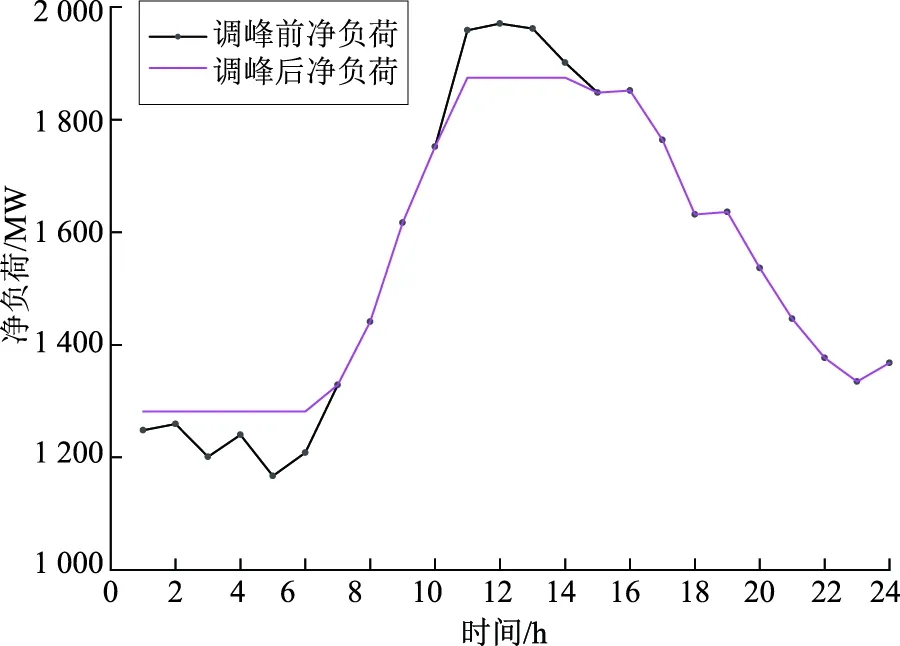
图5 调峰前后净负荷曲线Fig.5 Net load curves before and after peak shaving

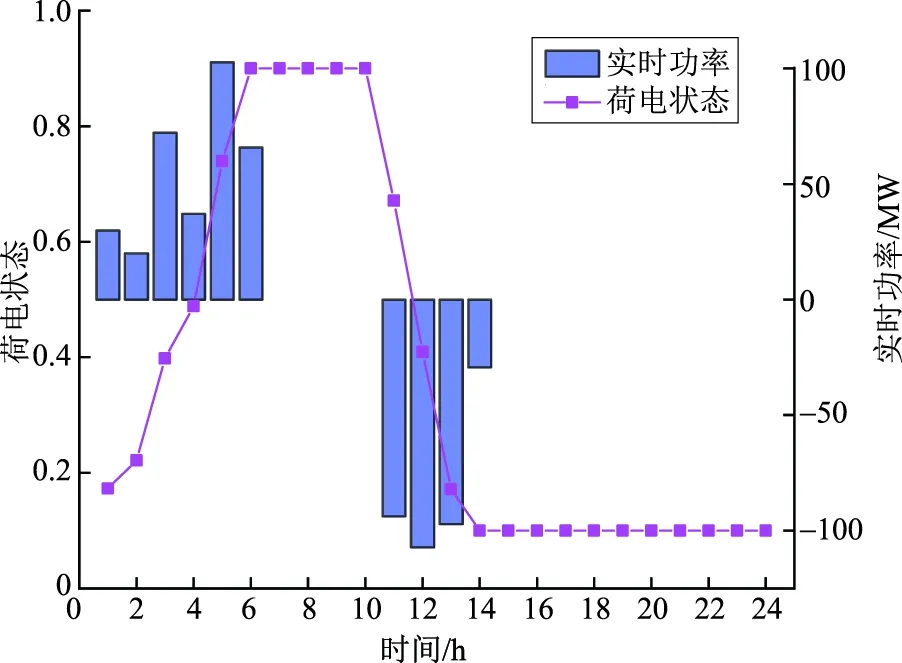
图6 储能系统实时功率及荷电状态Fig.6 Real-time power and state of charge of energy storage system

由图5可以看出，储能系统参与调峰可有效降低峰谷差率，达到削峰填谷的效果。此时调峰后净负荷峰值为1 874.57 MW，谷值为1 281.14 MW，峰谷差率为0.317，小于0.35，满足预期调峰效果。由图6可以看出，在一日内的任意时刻，储能系统的荷电状态均处于0.1～0.9之间，满足铅炭电池储能系统荷电状态要求。因此，基于M园区夏季调峰前后净负荷峰谷值、荷电状态等相关数据以及相关公式，可计算得出此时的铅炭电池储能系统的最优储能配置结果，即功率107.14 MW、容量409.33 MWh。

5.2.3 不同储能系统容量优化配置结果比较

由于不同电池储能系统的各项成本、使用年限、充放电功率损耗等不同，在考虑削峰填谷效果、荷电状态等多项约束下，其获得最大日净收益时所需要配置的储能系统的容量和功率均不同。为了选择恰当的储能系统参与调峰以获得更多收益，本文使用改进粒子群算法分别求解不同储能系统在满足上述约束条件下时所应配备的储能系统的功率和容量。由于每次运行结果有些微差异，本文对多次运行结果进行取平均值处理。以夏季储能容量优化配置为例，处理后的不同储能系统容量优化配置相关结果见表3。

表3 夏季不同储能系统容量优化配置结果Tab.3 Optimal configuration results of capacity of different energy storage systems in summer

由表3可知，铅炭电池、锂离子电池、钠离子电池3种储能系统最终得到的最优容量配置相差不大，调峰后的峰谷差率也差异很小，且均满足了预期调峰效果。从新增新能源消纳量来看，铅炭电池储能系统较多，锂离子、钠离子电池储能系统相差不大；从收益来看，锂离子电池和钠离子电池储能系统的收益相差不大，且比铅炭电池高许多；从成本来看，铅炭电池储能系统的成本最低，钠电子电池次之，锂离子电池最高；从日净收益来看，钠离子电池储能系统最高，铅炭电池次之，锂离子电池最低。分析原因，铅炭电池是因为其寿命短、充放电效率较低，锂离子电池主要是因为初始成本较高。综合上述考虑，建议选择钠离子电池组成储能系统参与调峰，其日净收益可达23.42万元，此时储能优化配置结果为功率109.96 MW、容量404.75 MWh。

5.2.4 园区M储能容量配置结果

基于园区M其他季节的典型日净负荷曲线，采用相同的策略和方法，使用改进后的粒子群优化算法求解对应的储能系统容量优化配置结果，见表4—6。

由表4—6可知：无论是基于哪个季节的典型日净负荷曲线，所求解的储能系统都应选择钠离子电池组成储能系统，这样既可以满足调峰效果约束，还能获得最大的净收益。为了满足所有季节需求，本文以典型负荷曲线中对储能需求最大的场景作为规划依据，确定M园区储能系统容量优化配置结果，即M园区应选择钠离子电池组成储能系统参与调峰，优化配置结果为功率153.65 MW、容量766.64 MWh。

表4 春季不同储能系统容量优化配置结果Tab.4 Optimal configuration results of capacity of different energy storage systems in spring

表5 秋季不同储能系统容量优化配置结果Tab.5 Optimal configuration results of capacity of different energy storage systems in autumn

表6 冬季不同储能系统容量优化配置结果Tab.6 Optimal configuration results of capacity of different energy storage systems in winter

6 结束语

本文针对储能参与调峰的容量优化配置进行研究，综合考虑了储能的充放电功率损耗、调峰效果、荷电状态、储能建设和运维成本、储能调峰各方面收益等诸多因素，提出了考虑储能调峰效果和经济性的储能调峰容量优化配置策略，以及用于求解的改进粒子群优化算法。最后，通过对L地区M工业园区储能调峰的容量进行优化配置，一方面证明了储能系统参与调峰的削峰填谷效果，另一方面验证了所提策略及改进粒子群算法的有效性。本文为考虑储能调峰效果的容量优化配置提供了参考，具有一定的实际价值。然而，本文未将其他调峰方式纳入研究范畴，需要在后续工作中作进一步的研究。