Unified description of different soils based on the superloading and subloading concepts

Yong Lu,Yu Jing,Wenxun Zhu,Yunfeng Bo,Gunlin Ye,Feng Zhng

a Department of Civil Engineering,Suzhou University of Science and Technology,Suzhou,215011,China

b Department of Civil Engineering,Shanghai Jiao Tong University,Shanghai,200240,China

c Suzhou Integrated Infrastructure Technology Research Institute (SITRI),Suzhou,215000,China

d Department of Civil Engineering,Nagoya Institute of Technology,Nagoya,466-8555,Japan

Keywords: Elastoplastic behavior Constitutive model Sand Clay State dependence

ABSTRACT Geotechnical engineering often involves different types of geomaterials,such as sandy soil and clayey soil.Existing studies have confirmed that these soils have some common features,i.e.their mechanical behaviors depend not only on the inherent characteristics but also on their initial states.To describe the main mechanical behaviors of different soils within a simple and reasonable constitutive framework is of great significance for the numerical analysis on geotechnical engineering.This paper first introduces a model based on the concepts of superloading and subloading,which considers the “state dependence”(effects of overconsolidation and structure)of soil and only adds two material parameters compared with the Cam-Clay model.Secondly,conventional triaxial tests are systematically carried out on four types of soils(i.e.sand,silty clay,clay,and intermediate soil)with different initial void ratios,and the mechanical similarities and differences of these soils are discussed uniformly.After that,six material parameters of these soils are uniformly determined based on the concepts of superloading and subloading,and then used in constitutive calculations to verify the feasibility.The calculated results show a good agreement with test data,indicating that the model based on the concepts of superloading and subloading has great potential for describing the general mechanical behaviors of different soils within a unified framework.This work is expected to be applied to constitutive selection and parameter determination in the geotechnical numerical analysis of complex soil profiles.

1.Introduction

The surface of the earth’s crust has undergone weathering,erosion,transportation and deposition processes,forming different types of sedimentary geomaterials (e.g.soft rock,sand and clay).For rock masses with internal structural planes,it is difficult to describe their mechanical behaviors within a framework of continuum mechanics (e.g.Steinhauser et al.,2009;Kamrin,2010;Zhang et al.,2012).Nevertheless,for sandy soil and clayey soil,they can be regarded as continuum medium,and numerous elastoplastic constitutive models can be constructed to describe their mechanical behaviors (e.g.Roscoe and Poorooshasb,1963;Bolton,1986;Dafalias and Herrmann,1986;Hashiguchi,1989;Yu,1998;Asaoka et al.,2000;Li and Dafalias,2000;Yao et al.,2009;Hashiguchi,2017).These models facilitate the description of sand or clay,while they also make practical applications lack uniformity and have challenges due to too many options.Whether it is possible to describe the main mechanical behaviors of different soils within a relatively simple and reasonable constitutive framework is of great significance for numerical analysis on geotechnical stability of complex soil profiles.

For the mechanical behaviors of soil,many experimental studies have been carried out.The main mechanical characteristics of soil can be summarized as follows.The first three characteristics are essential in determining the mechanical behaviors of soil,and are also the main difference between soil and other continuum materials.The mechanical behaviors of soil also depend on its physical state,which can be described as“state dependence”,including the stress history and the structure formed in the sedimentary environment as indicated in the 4th and 5th characteristics.

(1) Elastoplastic characteristic.Soil exhibits an obvious nonlinear elastoplastic mechanical behavior during loading.This makes the basic concepts in elastoplastic mechanics(i.e.yield characteristics,flow rule,and coaxial/non-coaxial behavior) applicable to the construction of soil constitutive models.

(2) Compressive hardening characteristic during compression.Roscoe and Poorooshasb (1963) carried out an isotropic compression test on the remolded saturated kaolin,and the normal consolidation line(NCL)can be described ase=eNλln(p/pN),whereeNis the reference void ratio for NCL under reference pressurepN(pNis often set to 1 kPa).This shows that during the isotropic compression of normally consolidated clay,the void ratioedecreases as the mean effective stresspincreases,and the slope decreases with the increase ofp.This indicates that the bulk modulus of the clay increases with thepvalue,which shows the performance of compressive hardening characteristics.In practice,since it is difficult to directly obtain the inherent/intrinsic NCL of sandy soil through experiments,the compressive hardening performance of normally consolidated clay provides a reference standard for the compressive characteristic of different soils(e.g.Yu,1998;Yao et al.,2012;Hashiguchi,2017;Mo and Yu,2018).

(3) Critical state characteristic during shearing.Roscoe and Schofield (1963) conducted triaxial shear tests on Weald Clay and found that the soil generally exhibits two types of critical state phenomena during the shearing process.One is the critical state of stress ratio (friction): the effective stress of the specimen remains unchanged after entering the critical state,and the ratio ofqf/papproaches a constant value,in whichqfis the deviatoric stress when entering the critical state.In thep-qplane,a linear function(qf=Mp)can be used to describe this characteristic,in whichMis defined as the critical strength parameter.This function essentially indicates soil’s friction property and is called the critical state line(CSL)of stress ratio.The other is the critical state of void ratio: the void ratio of the specimen will no longer change after entering the critical state,and it is approximately concentrated near a straight line parallel to NCL in thee-lnpplane,which is CSL of void ratio and can be described ase=eΓ-λln(p/pN),whereeΓis the reference void ratio for CSL under reference pressurepN.In addition,it was found in subsequent experimental studies that these two critical state phenomena exist in different soils (sandy soil and clayey soil),and the soil specimen will gradually approach the CSL of void ratio during compression and shearing,resulting in a macroscopic volume change,i.e.dilatancy (e.g.Rowe,1962;Roscoe and Burland,1968;Li and Dafalias,2000;Cai and Li,2004;Yang and Luo,2015;Lu et al.,2016).

(4) Stress history.Schofield and Wroth (1968) carried out isotropic unloading-reloading tests on overconsolidated clay.The test results show that the mechanical behaviors of clay are significantly affected by the degree of overconsolidation,and the clay undergoes a gradual accumulation of plastic strain during unloading-reloading process.Similarly,Li and Dafalias (2000) confirmed the correlation between the mechanical behaviors of sandy soil and its initial compaction degree based on numerous test results,and proposed a statedependent dilatancy equation by introducing a compaction state variable.From the perspective of compressive hardening characteristics,the compaction state of sandy soil or the overconsolidation state of clayey soil is essentially related to the stress history of soil,which will significantly affect the apparent mechanical behaviors of soil (e.g.Ishihara and Shigeru,1978;Gajo and Piffer,1999;Lee et al.,2011;Nishimura et al.,2011).

(5) Structure.The undisturbed soil in the natural sedimentary environment or the reinforced soil formed by artificial cementation,in which the particle connection is different from that in the remolded soil due to physical and chemical effects,is then called structured soil.Many experimental studies on the mechanical behaviors of structured soil have shown that under the same pressure,structured soil can maintain a larger void ratio than remolded soil.Besides,the compression curve of structured soil often has an obvious inflection point (yield point) and gradually approaches the compression curve of remolded soil after exceeds the yield point(e.g.Leroueil and Vaughan,1990;Cuccovillo and Coop,1997;Horpibulsuk et al.,2004;Zhang et al.,2018;Khalid et al.,2019).

To describe the above-mentioned essential mechanical characteristics and“state dependence”,numerous constitutive models of soil have been developed accordingly.Undoubtedly,the Cam-Clay model proposed by Roscoe et al.(1963) is the first one that can describe the essential mechanical characteristics of soil,including the above-mentioned 1st-3rd characteristics.However,since the classic Cam-Clay model has only one yield surface,plastic deformation cannot be accumulated when the stress state is inside the yield surface during the reloading process.This is inconsistent with the actual case and cannot reasonably describe the 4th characteristic.For this problem,some important development has been made based on the Cam-Clay model,such as the double-surface model (Krieg,1975),bounding surface model (Dafalias and Herrmann,1986),concept of subloading surface (Hashiguchi,1989,2017),and unified hardening model (Yao et al.,2009).The development of these models has promoted the understanding of“state dependence” of soils,making it possible to reasonably describe the mechanical behaviors of overconsolidated clay or compacted sand numerically(e.g.Lashkari,2009;Li et al.,2011;Wu et al.,2019).Furthermore,in order to describe the effect of structure formed in natural sedimentary environment (i.e.aforementioned 5th characteristic),Asaoka et al.(2000) and Asaoka et al.(2002)proposed the concept of superloading surface,which can describe the higher compressive modulus and the damage of structure.By combining superloading and subloading surfaces,the mechanical properties of overconsolidated soil and natural structured soil can be described uniformly within one constitutive framework,which is applied well in constitutive calculations (e.g.Zhang et al.,2007,2018;Ren et al.,2018;Khalid et al.,2021).Similarly,some other methods have been proposed to describe the influence of structure on the mechanical behaviors of soil,such as the moving NCL(MNCL)based on the unified hardening model(Zhu and Yao,2015),and the expanded yield surface based on the boundary surface(e.g.Yu et al.,2007a;Horpibulsuk et al.,2010;Suebsuk et al.,2011).Here,it needs to be explained that many factors,such as intermediate principal stress/Lode angle(e.g.Matsuoka et al.,1999;Sheng et al.,2000;Yao et al.,2009),time-dependent/rheological characteristic(e.g.Nakai et al.,2011;Oka et al.,2019),temperature (e.g.Hamidi et al.,2014;Xiong et al.,2019),unsaturation (e.g.Yao et al.,2014;Lloret-Cabot et al.,2017),principal stress rotation(e.g.Tian and Yao,2018;Xue et al.,2020),anisotropy(e.g.Borja et al.,2019;Yang et al.,2020),and micro-scale particle characteristics (e.g.Yang and Luo,2015;Alshibli and Cil,2018;Kawamoto et al.,2018;Lashkari et al.,2020;Cabalar et al.,2021) have been recognized and considered in soil mechanics.These have promoted the refined development of constitutive models and expanded numerical applications.Nevertheless,it should be emphasized that these factors can often be supplemented or expanded based on the abovementioned five main mechanical characteristics.Therefore,capturing and describing the main characteristics are still an important and fundamental task,which can provide direct and important guidance for most engineering applications.

The above-mentioned experimental and constitutive studies on the five mechanical characteristics of soil theoretically make it possible to uniformly describe the main mechanical behaviors of different soils at varied initial states.However,most of the existing studies generally focus on one or a few aspects of a specific soil and lack systematic discussion of characteristic parameters and unified calculation of mechanical behaviors for different soils.This cannot provide a valuable and effective reference for determining the material parameters of different soils in practice,which is often thought to be a bottleneck for engineers to use a sophisticated constitutive model.Therefore,this paper first introduces a theoretical framework based on the concepts of superloading and subloading,which considers the “state dependence” of soil and is expected to uniformly simulate the main mechanical characteristics of different soils at varied initial states.After that,conventional triaxial tests on the mechanical behaviors of soils (sand,silty clay,clay,and intermediate soil) with varied initial void ratios under different confining pressures are carried out systematically.Then,on the basis of the concepts of superloading and subloading,the material parameters of the above different soils are discussed and determined uniformly.Finally,the determined material parameters of four soils are used to carry out constitutive calculations to explore whether the main mechanical behaviors of different soils with varied initial states can be uniformly described based on the concepts of superloading and subloading.This work attempts to analyze and calculate the mechanical behaviors of different soils in one framework and is expected to be applied to the numerical analyses on geotechnical engineering problems of complex soil profiles from sandy to clayey soils.

2.Brief introduction of the concepts of superloading and subloading

2.1.Yield function

Based on the modified Cam-Clay model,Asaoka et al.(2000)presented the superloading surface concept to consider the influences of structure on the deformation and strength of undisturbed soil,and it was also combined with the subloading surface concept proposed by Hashiguchi (1989) to consider the influences of stress history(overconsolidation/compaction degree).After that,a constitutive model containing three similarly shaped yield surfaces is proposed to comprehensively consider the effects of overconsolidation and structure on the mechanical behaviors of soil.

The three yield surfaces,i.e.subloading surface,normal yield surface,and superloading surface,as shown in Fig.1,have been applied and extended by many researchers(e.g.Zhang et al.,2007,2011;Ye and Ye,2016;Ye et al.,2018;Lu et al.,2021).The normal yield surface depends on the normal consolidation stress corresponding to the plastic volumetric strain,which is the same as the Cam-Clay model.The subloading surface is where the current stress is located,and it varies during both loading and unloading processes.This can describe the effects of overconsolidation,especially the plastic deformation that occurs during reloading.The superloading surface describes the potential compressive yield stress,which considers the effects of structure.The similarity ratio(R*)of normal yield surface to superloading surface is adopted to represent the degree of structure,and the similarity ratio (R) of subloading surface to superloading surface is adopted to represent the degree of overconsolidation.

Fig.1.Yield surfaces based on the concepts of superloading and subloading: (a) p-q stress plane,and (b) e-lnp plane.

where,andpmrepresent the positions of superloading surface,normal yield surface,and subloading surface inp-qstress plane,respectively.

By adoptingR*andRto represent the degree of structure and overconsolidation,the subloading surface where the current stress state is located can be derived as follows:

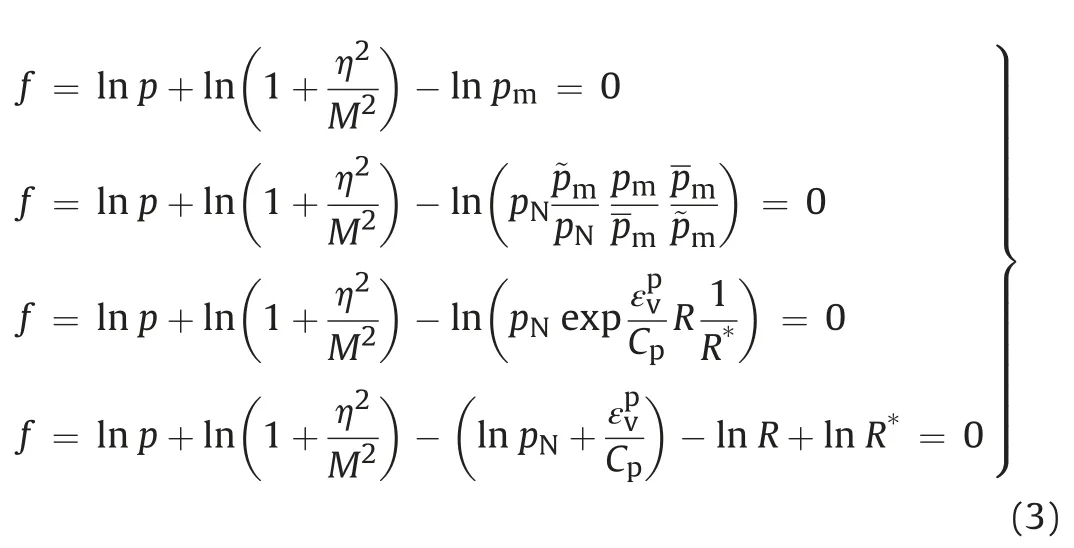
The variables involved in Eq.(3) are expressed as

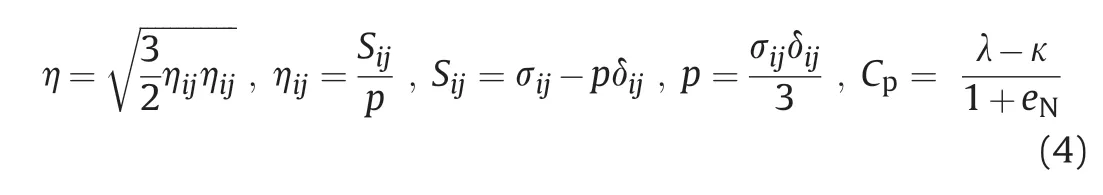
2.2.Evolution rules of overconsolidation and structure

Here,the evolution rule of overconsolidation in Asaoka et al.(2000) was adopted and was controlled by the norm of plastic strain increment tensor.In addition,an additional factorUproposed by Zhang et al.(2007) in the cyclic mobility model was also introduced so that the model can consider the static liquefaction state that may occur during the undrained shearing process(Eq.(5)).If the soil is near liquefaction state (i.e.mean effective stresspbecomes small),the value ofUis almost equal to zero.This makes it possible to generate a large plastic shear strain with small overconsolidation change near the liquefaction state,and it is in agreement with actual case.

wheremis a parameter that defines the evolution rate ofR,and the norm of plastic strain increment tensoris

The evolution rule of structure defined by Asaoka et al.(2000)and Asaoka et al.(2002) is a function of plastic deviatoric strain.However,some experimental studies on structured soils have confirmed that both plastic volumetric strain and plastic deviatoric strain can result in structure loss,and the structure can also be damaged during isotropic compression (e.g.Lagioia and Nova,1995;Horpibulsuk et al.,2004;Nguyen et al.,2017).In current study,the structure evolution is supposed to be relevant to the norm of plastic strain increment tensor(Eq.(7)),which is the same as Ye and Ye(2016).

whereais a parameter that controls the structure damage rate during the loading.According to the definition,it is obvious that dR*is positive beforeR*reaches one,representing the damage of structure.WhenR*reaches one,dR*approaches zero,indicating that the structure will never be recovered once lost.

Based on Eqs.(5) and (7),the evolutions of structureR*and overconsolidationRwith different parameters(aandm)are shown in Fig.2,where the parametersMandCpare assumed to be 1.8 and 0.015,respectively.It can be well described that the overconsolidationRand the degree of structureR*gradually evolve with the accumulation of plastic strain,and largeraormbring faster evolution.

2.3.Material parameters and initial state variables

There are seven material parameters,i.e.M,eN,λ,κ,ν(Poisson’s ratio),aandm,involved in the model here,and the first five parameters are consistent with those of the Cam-Clay model(Roscoe et al.,1963).

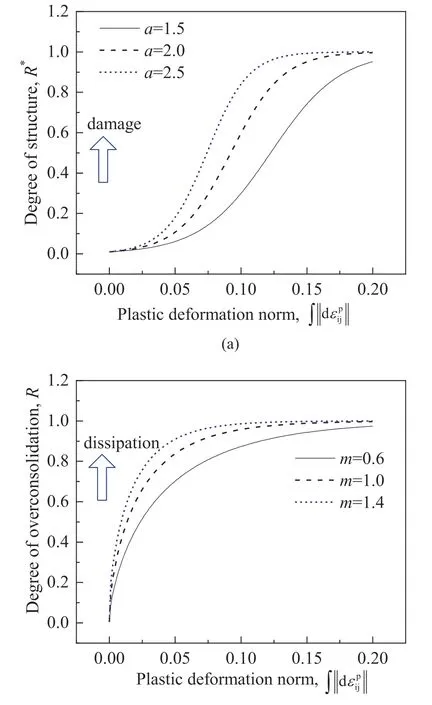
Fig.2.The evolution of (a) R* and (b) R with different parameters.

In the concepts of superloading and subloading (Hashiguchi,1989;Asaoka et al.,2000),the mechanical behaviors of soil under loading depend on inherent/intrinsic properties and initial states,which are relevant to the history it has experienced.For the model here,there are four initial state variables:pm0(kPa): initial mean effective stress;e0: initial void ratio under initial mean effective stresspm0;: initial degree of structure;andR0: initial degree of overconsolidation.

Based on the above-mentioned yield function,evolution rules of state variables and material parameters,the stress increment tensor can be calculated with the consistency equation (see Appendix A).

3.Laboratory tests

To explore whether the mechanical behaviors of different soils can be uniformly described based on the concepts of superloading and subloading,this study first carried out conventional triaxial tests on different soils,such as sandy soil,clayey soil and intermediate soil (sand with fine grains),to obtain their mechanical properties.

3.1.Different soils

The sandy soil used in this study is a type of China ISO standard sand with quartz as the main component,i.e.Fujian sand.Its particle size distribution(PSD)curves,X-ray diffraction(XRD)patterns,and scanning electron microscope (SEM) images are shown in Fig.3,and the key physical properties are presented in Table 1.Besides,the maximum and minimum void ratios are obtained following GB/T 50123 (2019).

The two types of clayey soils used in this study were collected in Suzhou at southeastern China.Their PSD curves,XRD patterns,and SEM images are also shown in Fig.3.The clayey soil paste was first dried and crushed and then passed through a 2 mm sieve for removal of shell pieces and other large particles.Finally,its physical properties were tested.The physical properties of the two clayey soils listed in Table 2 were also obtained following GB/T 50123(2019).These two clayey soils can be classified as silt clay and clay according to GB/T 50145 (2007) and can also be classified as lean clay according to ASTM-D2487 (2011).

Table 1 Physical properties of Fujian sand.

Table 2 Physical properties of two types of clayey soils.

The intermediate soil used in this study is a mixture of Fujian sand and silty clay with a certain mass ratiorr(i.e.the dry weight ratio of clayey soil to sandy soil).It should be emphasized that the mechanical properties of intermediate soil will be inevitably affected by the content of coarse and fine particles (i.e.Thevanayagam and Mohan,2000;Naeini and Baziar,2004;Monkul and Ozden,2007;Cabalar and Hasan,2013;Monkul et al.,2021),but this is not the focus of the research here.In this study,theintermediate soil mixed with coarse and fine particles in a certain mass ratio was used as one type of soil to systematically discuss the similarities and differences of the mechanical behaviors of different soils (i.e.sand,silty clay,clay,and intermediate soil) to comprehensively verify the applicability of the subloading surface concept.It should also be noted that the research here is aimed at element test and constitutive calculation,thus the uniform distribution of coarse and fine particles in the intermediate soil sample is important.Otherwise it should be discussed within the framework of the boundary value problem.Therefore,for the intermediate soil sample,there is one thing in detail that should be noted during preparation.During the compaction and saturation stages of sample preparation,the clayey particles with small content are easy to deposit to the bottom of the sample,resulting in nonuniformity (Fig.4a).To overcome this problem,the preliminary test of sample preparation was carried out,and it was determined that mass ratiorr=50%combined with moist tamping method(e.g.Ni et al.,2021) is suitable for the preparation of uniform intermediate soil samples(Fig.4b).Accordingly,de-aired water with a mass ratio of 5% was added to the intermediate soil in advance,stirred evenly,and then stored in a sealed bag to ensure uniform moisture(Fig.4c).

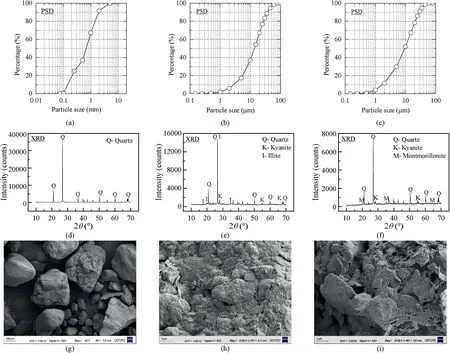
Fig.3.PSD curves of (a) sand,(b) silty clay and (c) clay,XRD patterns of (d) sand,(e) silty clay and (f) clay,and SEM images of (g) sand,(h) silty clay and (i) clay.

3.2.Test procedure

For different soils mentioned above,drainage triaxial tests of samples with different initial void ratios (dry density) under different confining pressures were carried out.This is to systematically verify the applicability of the model based on superloading and subloading surfaces,especially their advantages in describing the“state dependence”of soil.The test scheme is shown in Table 3,and each group of tests includes 2-3 parallel specimens to ensure the reliability of test results.

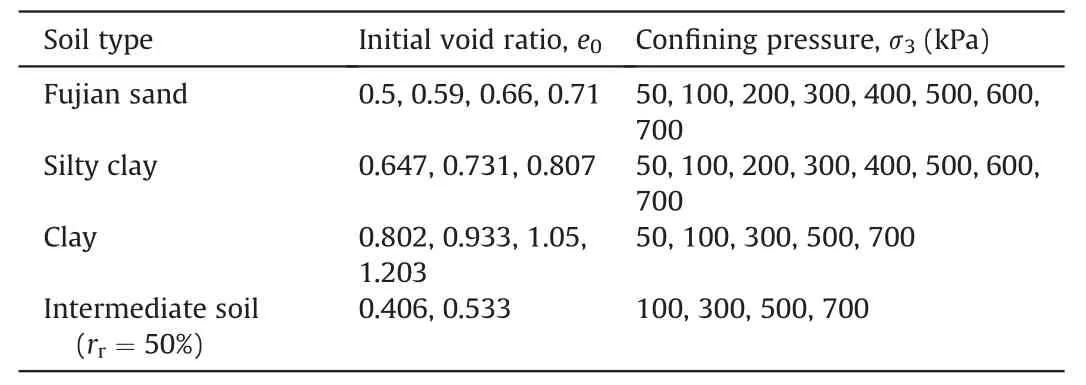
Table 3 Test scheme for different soils.

As shown in Fig.5,for a certain initial void ratio,the weight of dry soil for a specimen can be calculated by the weight-volume relations,as shown in Eqs.(8) and (9).The calculation processes for different soil are the same.When Eqs.(8) and (9) are used for the calculation of single soil instead of intermediate soil,rrneeds to be set to zero or infinity.

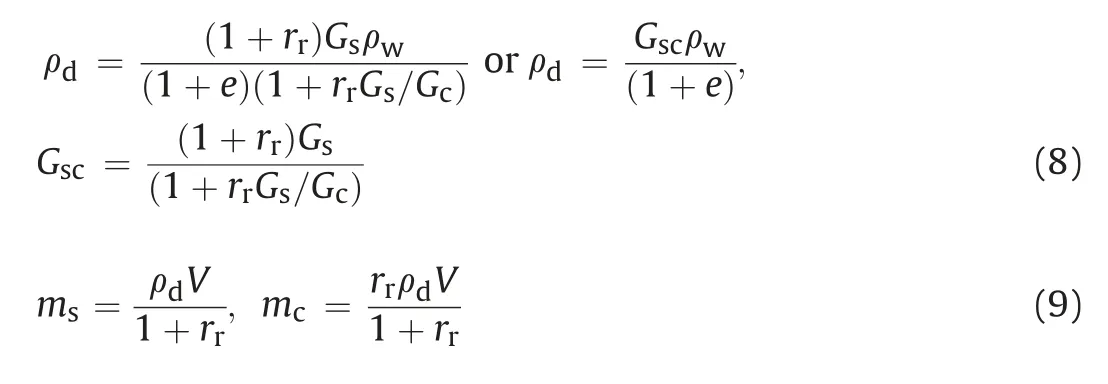
whereGsandGcare the specific gravity values of sandy soil and clayey soil,respectively;ρwis the density of water;Vis the volume of the specimen with diameter (d) of 39.1 mm and height (h) of 80 mm;ρdandGsccan be regarded as the equivalent density and equivalent specific gravity of intermediate soil,respectively;andmsandmcare the dry weights of sandy soil and clayey soil,respectively.

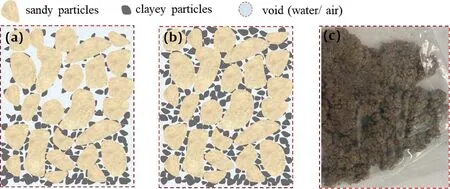
Fig.4.Preparation of intermediate soil:(a)Non-uniform,(b)uniform,and(c)stored in a sealed bag.

For the preparation of sandy soil and intermediate soil specimens,GB/T 50123(2019)was followed.A split mold placed on the base of the test apparatus was used to fabricate specimens(Fig.6a).To obtain a uniform specimen,the predetermined weight of dried sand(or moist intermediate soil)was deposited into the split mold in five layers with the aid of a long-neck funnel(or spoon)(Fig.6b).Each layer can be slightly compacted by a flat-bottom tamping rod to achieve the desired void ratio (Fig.6c).Then,filter paper,permeable stone,and loading cap were placed on top of the specimen in sequence(Fig.6d).After that,a small suction(negative back pressure) of-5 kPa was applied to the specimen to avoid collapse when removing the mold and kept unchanged until the confining pressure was increased to 5 kPa to maintain the specimen.Finally,CO2gas first flushed gently from the bottom of the specimen to replace the air,followed by the infiltration of de-aired water under a low pressure to saturate the specimen (Fig.6e).

For the preparation of clayey soil specimen,the process is somewhat different from that of sandy soil.The dried clayey soil with predetermined weight was divided into five parts with equal mass and then deposited into a separate split mold in five layers(Fig.7a).Each layer was also compacted by the flat-bottom tamping rod to achieve the desired void ratio (Fig.7b).Different from the saturation process of sandy soil or intermediate soil,the clayey soil must be saturated in vacuum by de-aired water for about 24 h before the test using a saturation container(Fig.7c).After that,the saturated specimen was taken out and placed on the base of the triaxial apparatus.Filter paper,permeable stone,and loading cap were placed on the top of the specimen in sequence (Fig.7d).Finally,the confining pressure was increased to 5 kPa as the initial stress state (Fig.7e).

To obtain high saturation for all specimens,a back pressure of 100 kPa was applied,and the confining pressure was increased simultaneously to keep the effective confining pressure at 5 kPa.Through these steps,the measured Skempton’sBcoefficient of all specimens was larger than 0.98.Then,the predetermined confining pressure was applied to the specimen for isotropic consolidation.After the consolidation was completed,drained shearing processes at 1 mm/min,0.005 mm/min,and 0.05 mm/min were performed for sandy soil,clayey soil,and intermediate soil,respectively,considering the difference in permeability of soils.

3.3.Results and discussion

For different soils with varied initial states,the relationships between deviatoric stress and axial strain,and that between volumetric strain and axial strain can be directly obtained through conventional drainage triaxial tests.The detailed test results are presented and compared with constitutive calculations in Section 5.Here,to uniformly determine the material parameters of different soils,the main characteristics related to strength and deformation are discussed first.

Fig.5.Schematic diagrams of different soils.

Fig.6.Specimen preparation of sandy soil and intermediate soil: (a) Spilt mold,(b) long-neck funnel or spoon,(c) flat-bottom tamping rod,(d) assembled situation,and (e)specimen saturation.

3.3.1.Peak or residual stress ratio of different soils with different initial states

Fig.8 shows the peak or residual stress ratio of different soils with varied initial void ratios obtained in conventional drainage triaxial tests.The peak stress ratio corresponds to the peak point of the stress-strain relation(i.e.Rp=σp/σ3,where σpis the peak stress during the shearing process).The residual stress ratio corresponds to the approximately stable stage of the stress-strain relation (i.e.Rf=σf/σ3,where σfis the residual stress corresponding to the stable stage during the shearing process).It can be seen from Fig.8a that the Fujian sand in this study has an obvious peak point of the stress-strain relation (i.e.strain softening),and this phenomenon gradually weakens with the increase of initial void ratioe0and confining pressure σ3.This actually shows the “state dependence”of the mechanical properties of sand,which has attracted many researchers’attention(e.g.Lee et al.,2011;Li et al.,2011;Mo and Yu,2018;Ye et al.,2018;Lu et al.,2021).Another important phenomenon is that all the different soils in this study approximately have their own stable stage during the shearing process,and the residual stress ratio corresponding to this state is not significantly affected by the initial void ratioe0and confining pressure σ3(Fig.8a-d).Meanwhile,it should be noted that when the confining pressure becomes larger,the axial strain required to approach the stable stage also becomes larger,which makes the residual stress ratio slightly affected by the confining pressure.

Fig.7.Specimen preparation of silty clay and clay: (a) Deposition of soil,(b) flat-bottom tamping rod,(c) specimen saturation,(d) assembled situation,and (e) application of confining pressure.

Fig.8.Peak stress ratio Rp or residual stress ratio Rf with varied initial states of different soils: (a) Fujian sand,(b) silty clay,(c) clay,and (d) intermediate soil (rr=50%).

The above results on the stress ratio also confirm the rationality of the concepts of superloading and subloading.The peak stress ratio is largely dependent on the physical state of the soil(i.e.void ratio and mean effective stress),thus it cannot be used as an inherent characteristic parameter of the soil.In contrast,the residual stress ratio is basically not affected by the physical state of the soil and can be used to approximately determine the CSL of stress ratio,which depends on the friction properties of the soil(e.g.Ye and Ye,2016;Patil et al.,2017;Lu et al.,2021).

3.3.2.Isotropic consolidated void ratio of different soils with varied initial states

Fig.9 shows the isotropic consolidation curves of soils with different initial states obtained from the conventional drainage triaxial tests.The isotropic consolidation curves of each soil with different initial states vary,which further confirms the “state dependence”of soil mechanical behavior.It is worth noting that the isotropic consolidation characteristics of sandy soil are different from that of clayey soil and intermediate soil.For clayey soil and intermediate soil,as the consolidation pressure increases,the consolidation curves gradually approach and eventually converge to an inherent curve unrelated to the initial void ratio (Fig.9b-d).According to the concepts of superloading and subloading,this inherent curve is the NCL proposed in critical state of soil mechanics (Roscoe et al.,1963),and it can be described ase=eN-λlnp.For sandy soil,the consolidation curves with different initial states also tend to converge as the consolidation pressure increases,but it is difficult to converge to an inherent curve within a limited confining pressure range,as shown in Fig.9a.This phenomenon has been mentioned in many studies on sandy soil,and it is generally believed that the inherent curve NCL of sandy soil is more difficult to obtain than that of clayey soil(e.g.Cubrinovski and Ishihara,1998;Yu,1998).In practice,NCL of sandy soil is often assumed by calculating and fitting specific test results (e.g.Yu,1998;Asaoka et al.,2000;Yu et al.,2007b;Zhang et al.,2007).

3.3.3.Critical void ratio of different soils with varied initial states

Fig.10 shows the relation between the void ratio and mean stress for different soil specimens at stable stage during the shearing process.A common phenomenon is that the void ratio of specimens will eventually approach to a stable value related to the mean effective stress during the shearing process,and the relation can be approximately described ase=eΓ-λlnp.This is actually the CSL of void ratio proposed in critical state soil mechanics (Roscoe et al.,1963) and its slope is basically consistent with the corresponding NCL in thee-lnpplane.However,it should be mentioned that the test results here show that the CSL of sand is affected by the initial void ratioe0,and this effect is more significant in dense sand than in loose sand.As shown in Fig.10a,when the initial void ratioe0increases to 0.66,the position of CSL will gradually stabilize.This indicates that the CSL of sand is not unique,and the CSL of dense sand needs to consider the influence of the initial void ratio of the sample,which is different from clayey soil or intermediate soil.The reason for this issue may be related to the strain localization phenomenon that often occurs in dense sand (volume change occurs locally in the sample) (e.g.Hazeghian and Soroush,2016;Huang et al.,2018).The non-uniform deformation of dense sand affects the overall dilatancy or shrinkage of the sample during the shearing process,making it difficult for the sample to reach the critical state as a whole.This issue is worthy of further investigation by taking strain localization as a boundary value problem.

Fig.9.Isotropic consolidation curves of(a)Fujian sand,(b)silty clay,(c)clay,and(d)intermediate soil(rr=50%)with varied initial states obtained in conventional drainage triaxial tests.

4.Determination of material parameters

Based on the concepts of superloading and subloading,the material parameters(M,eN,λ,κ,ν,m,a)and initial state variables for each soil are uniformly determined.

4.1.Material parameters related to critical state mechanics (M,eN,λ, κ, ν)

It should be emphasized that five parameters (M,eN,λ,κ,ν)are the same as those in the Cam-Clay model,and they belong to the category of critical state soil mechanics proposed by Roscoe et al.(1963).In other words,these five parameters are inherent characteristic parameters independent of the physical state of soils.

ForM,it is related to the residual stress ratio rather than the peak stress ratio during the loading process.According to the concepts of superloading and subloading,the peak stress ratio is not an inherent characteristic parameter of soil but is related to the physical state,such as overconsolidation and structure.This viewpoint has also been confirmed by the results in Section 3,i.e.the peak stress ratio changes with the initial state of soil,while the residual stress ratio is almost constant.Accordingly,the residual stress ratioRffor each soil can be used to calculate the critical strength parameterM,as shown in Eq.(10).The calculatedMfor each soil in this study is listed in Table 4.

ForeNand λ,they are related to the compressive characteristics of soil.As mentioned in Section 3,for clayey soil and intermediate soil,the consolidation curves gradually approach and eventually converge to an inherent curve that is not related to the initial void ratio.This inherent curvee=eN-λlnpis exactly the NCL proposed in the critical state soil mechanics (Roscoe et al.,1963).Therefore,theeNand λ of silty clay,clay,and intermediate soil in this study can be obtained directly from the test results(see Fig.9),and the values are listed in Table 4.

However,the consolidation curves for sandy soil with different initial void ratios are not easy to converge to an inherent curve within a limited confining pressure range,making it difficult to obtain the NCL for sandy soil (Fig.9a).Fortunately,a common phenomenon is that during the shearing process,the void ratios of specimens with different initial void ratios will eventually approach a set of stable curves parallel to each other and can be approximately described ase=eΓ-λlnp(Fig.10a).These curves are similar to the CSL of void ratio in critical state soil mechanics,and the slope λ can be determined to be consistent with corresponding NCL in thee-lnpplane,which can be used to indirectly determine the parameter λ for sandy soil.Besides,the modified Cam-Clay model proposed that the distance between NCL and CSL in thee-lnpplane satisfies Eq.(11).The detailed derivation of this equation is presented in Appendix B,which has been applied in many existing works (e.g.Asaoka et al.,2000;Yu et al.,2007b;Zhang et al.,2018).Accordingly,the parametereNof sandy soil with different initial void ratios can be determined indirectly based on the set of parallel curves similar to CSL.In this way,for sandy soil,λ andeNrelated to initial void ratio can be obtained,and the values are listed in Table 4.

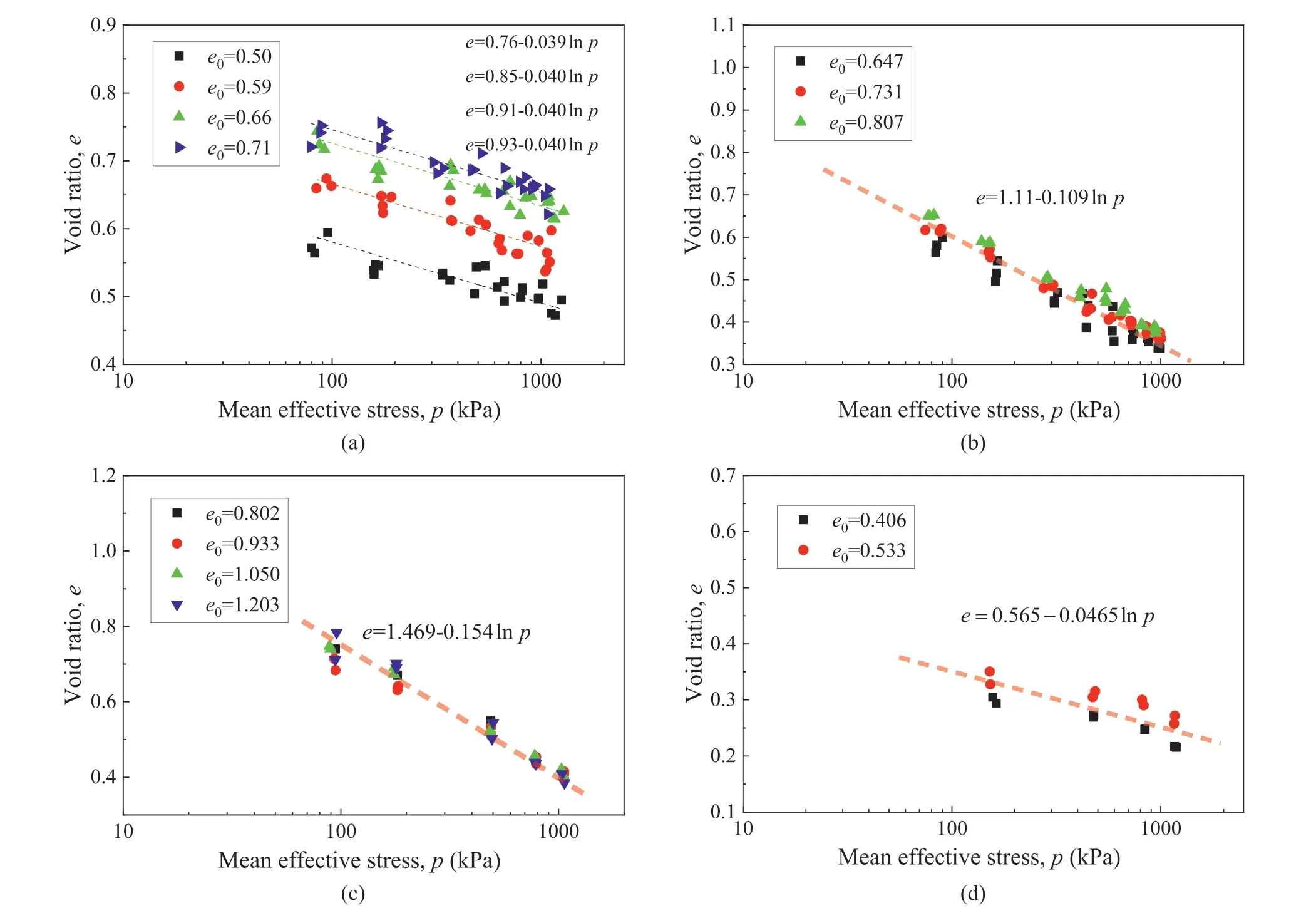
Fig.10.Critical void ratio of (a) Fujian sand,(b) silty clay,(c) clay,and (d) intermediate soil (rr=50%) with varied initial states obtained in triaxial tests.

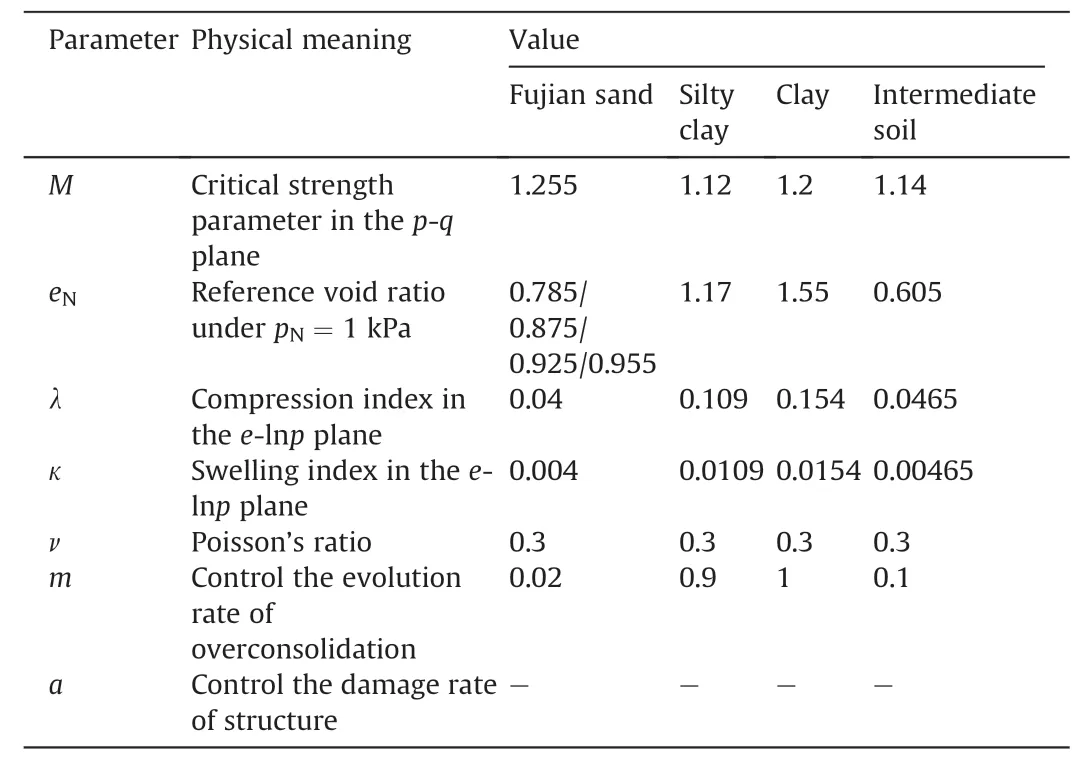
Table 4 Material parameters of different soils.

For κ and ν,they describe the elastic swelling characteristic and the elastic Poisson’s effect,respectively.Empirically,for soil,the swelling index κ is generally 0.1-0.15 times the compression index λ,thus the value in this range is not sensitive when used in the calculation ofeNin Eq.(11) andCpin Eq.(4).The Poisson’s ratio is generally 0.25-0.35.This value is also not sensitive when used to determine the elastic modulusEin Eq.(A4),especially for elastoplastic response.In this study,for different soils,the swelling index κ is approximately taken as 0.1 times the compression index λ,and the Poisson’s ratio is uniformly taken as 0.3,as listed in Table 4.

4.2.Initial state variables

According to the concepts of superloading and subloading,the mechanical behaviors of soil under loading depend on the inherent material parameters and initial states.Therefore,the initial state variablespm0,e0,andR0for each soil need to be determined first.The initial mean effective stresspm0and initial void ratioe0can be determined directly from the specimen.In this study,there is no confining pressure for the prepared specimen.Butpm0is set to asmall value of 5 kPa for the convenience of calculation as shown in Table 5.

Table 5 Initial state variables of different soil specimens.

For the initial degree of structure,it is difficult to determine directly because it is relevant to the history of soil formation.According to the concepts of superloading and subloading,describes the strengthening effect of structure on the mechanical properties of soil.It can be estimated empirically by the following methods.Firstly,the initial normal consolidation stressthat determines the initial position of normal yield surface can be obtained according to Eq.(12),and the detailed derivation is presented in Appendix C.Secondly,the potential compressive yield stressthat determines the initial position of superloading surface can be obtained from the isotropic consolidation curve,and the value corresponds to the inflecting/turning point in thee-lnpplane(Fig.1).Finally,can be calculated by Eq.(13),which is used to describe the degree of structure in the concepts of superloading and subloading surfaces.

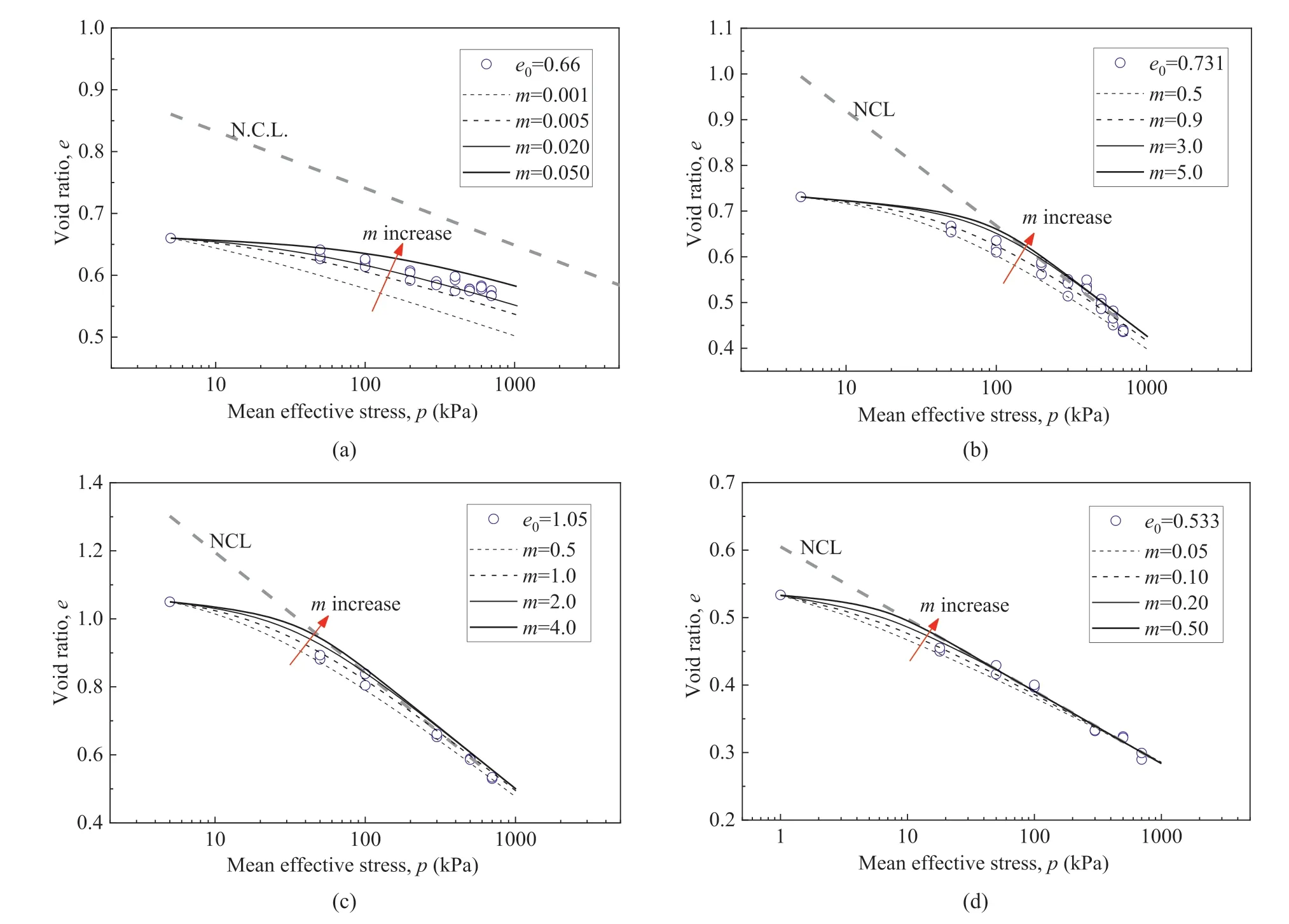
Fig.11.Fitting lines of parameter m based on isotropic compression results of (a) Fujian sand,(b) silty clay,(c) clay,and (d) intermediate soil (rr=50%).

It should be pointed out that only disturbed and remolded soils are under consideration in this study.A systematic analysis of different types of undisturbed soil will be the next important task.Therefore,the four remolded soils in this study do not possess an initial structure,and the corresponding0is set to 1 (i.e.=～pm0).Another issue is that,in the concepts of superloading and subloading,the initial degree of overconsolidation(R0)includes the effects of both structure and conventional compaction degree(Fig.1),and it can be calculated from other known initial state variables

4.3.Fitting for m and a

The two parametersmandahave clear physical meanings,where parametermdefines the evolution rate of overconsolidation,and parameteradefines the damage rate of structure.They are also inherent parameters in the concepts of superloading and subloading.However,they are related to the evolution of state variables which are different from the critical state parameters in the Cam-Clay model.Therefore,these two parameters cannot be derived from the test results when the specimen enters the critical state,because the state variable at this time has completely evolved(R=1,R*=1).In practice,these two parameters need to be determined by calculating and fitting the test results,which have been explained in previous studies (Zhang et al.,2007;Ye and Ye,2016).

There is no need to consider the structure evolution for the four types of remolded soil in this study.Only the parametermneeds to be calculated and fitted here,as shown in Fig.11,and the corresponding values are listed in Table 4.It should also be mentioned that for any specific soil,once these parameters are determined,the same set of parameters will be used regardless of the loading conditions and initial states.This is actually the advantage of the concepts of superloading and subloading,which reasonably considers the “state dependence” of soil and its evolution.

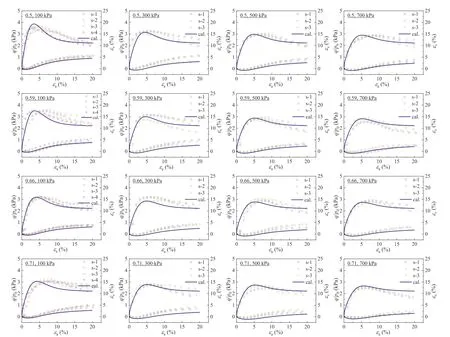
Fig.12.Test results of Fujian sand and the corresponding constitutive calculations under different initial void ratios and confining pressures.

From Table 4,it is found that there are some meaningful regularities among the material parameters of different soils: (1) The critical strength parameterMof sandy soil is generally larger than that of clayey soil.This difference is essentially related to the friction properties of the mineral composition of the soil particles;(2)The compression index λ of sandy soil or intermediate soil is significantly smaller than that of clayey soil,which actually describes the difference in the compressive hardening characteristics of different soils;(3) Instructively,similar to the difference in compression index λ,the parameter controlling the evolution rate of overconsolidationmfor sandy soil or intermediate soil is also significantly smaller than that of clayey soil,indicating that there is a certain correlation betweenmand λ.These regularities will provide an important and effective reference for determining the material parameters of different soils in practice.

5.Verification

Fig.13.Test results of silty clay and the corresponding constitutive calculations under different initial void ratios and confining pressures.

In this section,the determined material parameters for each soil will be used to carry out constitutive calculations to explore whether the general mechanical behaviors of different soils with varied initial states can be uniformly described based on the concepts of superloading and subloading.The results show the relation between normalized stress ratioq/p0,volumetric strain εvand axial strain εa.

5.1.Fujian sand

Fig.12 shows the test and calculated results of Fujian sand with varied initial void ratiose0under different confining pressuresp0.It can be seen that Fujian sand exhibits the following characteristics:(1)The specimens with differente0(0.5-0.71)in this study exhibit the characteristics of strain softening and shear dilatancy under differentp0values (100-700 kPa) and show a weakening trend with the increase ofp0;(2)Under the samep0,the peak stress ratio corresponding to the peak point of theq/p0-εarelation decreases with the increase ofe0,i.e.the strain softening phenomenon gradually weakens with the increase of initial void ratio.In general,the results actually show the“state dependence”of the mechanical properties of soil(Lee et al.,2011;Mo and Yu,2018;Ye et al.,2018;Zhang et al.,2018;Khalid et al.,2019;Lu et al.,2021).The calculations here basically in agreement with the test results,indicating that the model based on the concepts of superloading and subloading can well describe the main mechanical behaviors of sandy soil.

5.2.Clayey soil

Figs.13 and 14 show the test and calculated results of the silty clay and clay with varied initial void ratiose0under different confining pressuresp0.It can be seen that the two types of clayey soil exhibit the following characteristics: (1) The specimens with differente0values mainly exhibit strain hardening and shear contraction under differentp0values(100-700 kPa),except for the clay withe0=0.8 which shows a certain strain softening and shear dilatancy under 100 kPa;(2)The stress ratioq/p0at a certain axial strain εatends to decrease with the increases ofe0andp0,indicating that the development of shear stress is affected by initial void ratio and confining pressure.This also shows the “state dependence”mentioned in some existing researches(e.g.Lee et al.,2011;Zhang et al.,2018;Khalid et al.,2019).The calculation results are also in agreement with the test results,indicating that the model based on the concepts of superloading and subloading can also well describe the main mechanical behavior of clayey soil.

Asp0increases to 700 kPa,there is a certain difference between the calculated and test results,i.e.the test value ofq/p0is generally smaller than the corresponding calculated value.The reason may be that the consolidation process under high confining pressure makes the void ratio of the specimen smaller,which reduces the permeability of the specimen and makes it difficult for the internal pore water pressure to dissipate.This makes the shear stress determined by the effective stress not fully developed and limits the volumetric strain during shearing process,which is measured by the drainage volume.

5.3.Intermediate soil

Fig.15 shows the test and calculated results of the intermediate soil with varied initial void ratiose0under different confining pressuresp0.It can be seen that the intermediate soil exhibits the following characteristics: (1) The specimens with differente0values (0.406 and 0.533) exhibit strain hardening and shear contraction characteristics under differentp0values (100-700 kPa);(2) Under thep0of 100 kPa and 300 kPa,the initial stiffness(i.e.the initial slope ofq/p0-εa)corresponding toe0=0.406 is slightly larger than that corresponding toe0=0.533,indicating that the development of the shear stress is affected by the initial void ratio,showing “state dependence”.

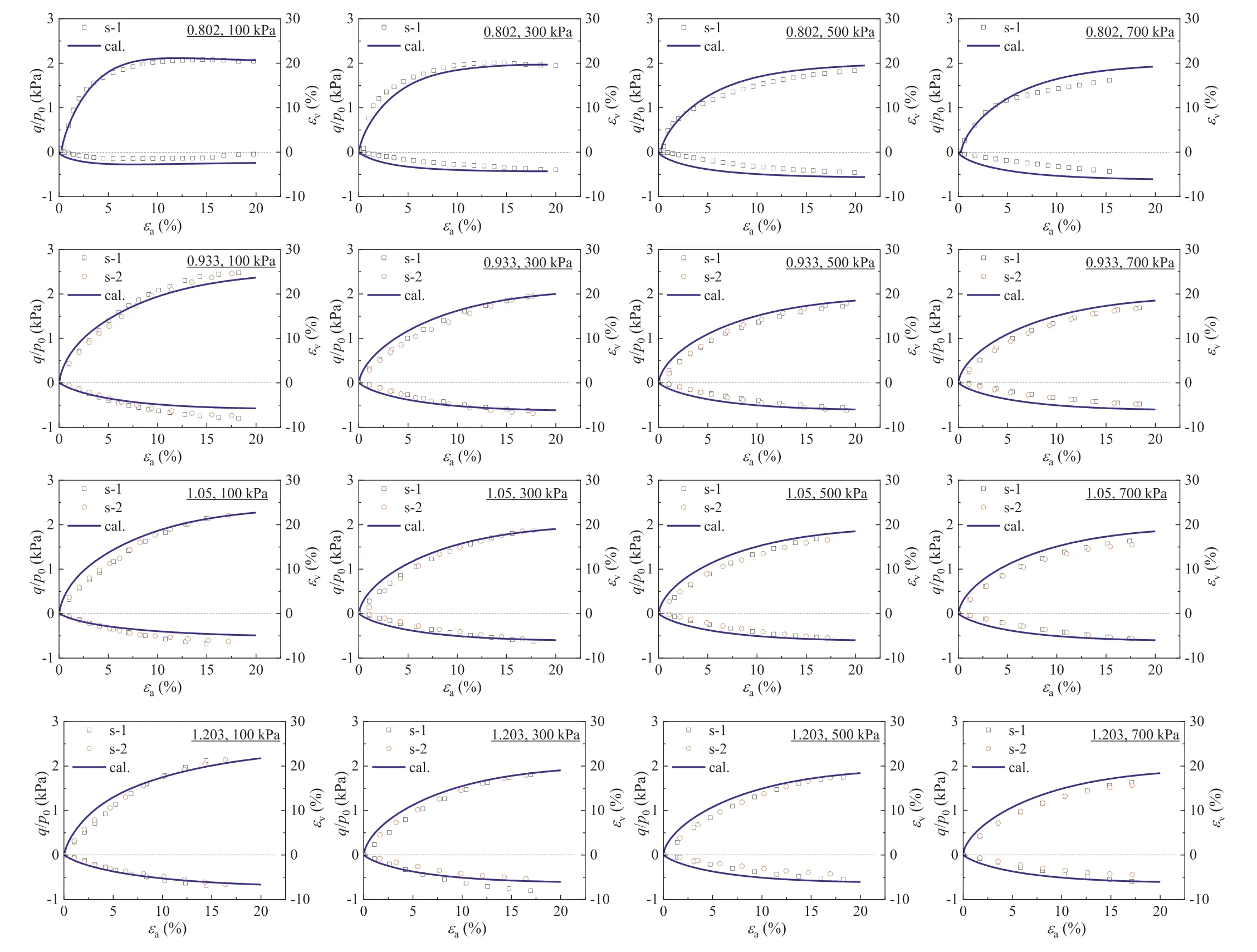
Fig.14.Test results of clay and the corresponding constitutive calculations under different initial void ratios and confining pressures.

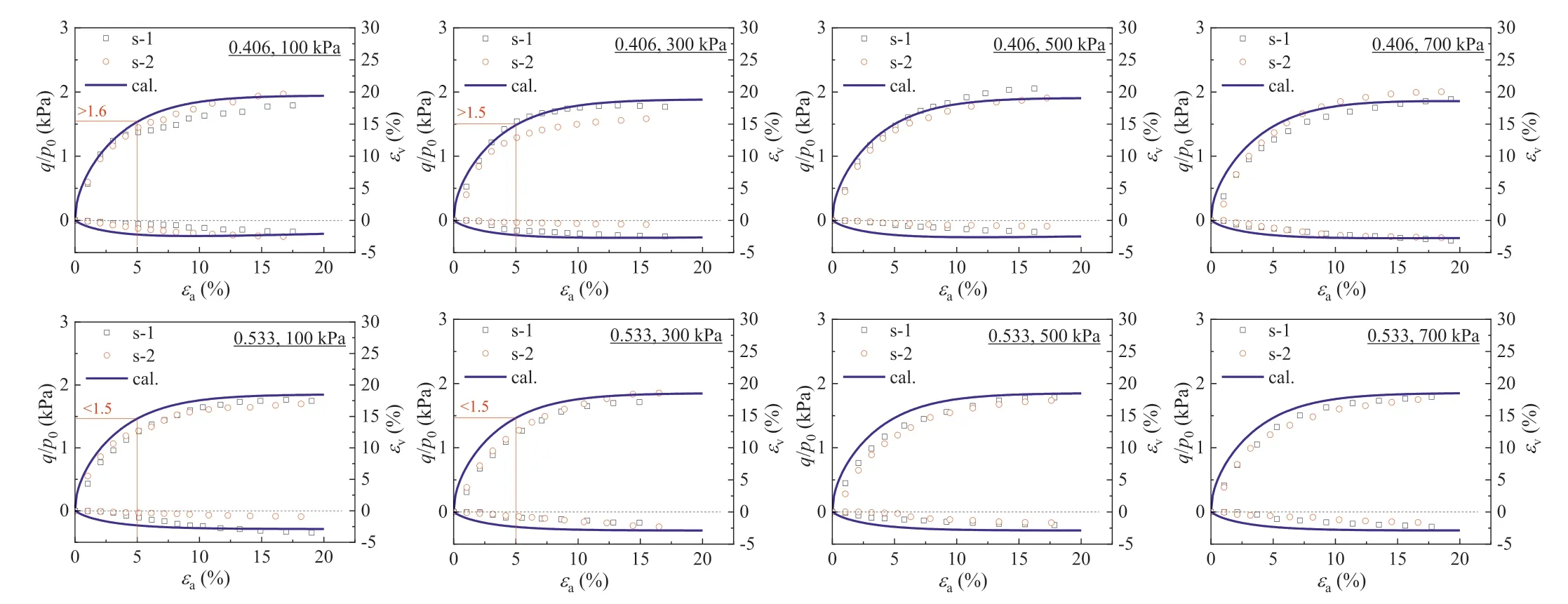
Fig.15.Test results of intermediate soil and the corresponding constitutive calculations under different initial void ratios and confining pressures.

As mentioned above,the intermediate soil mixed with coarse and fine particles in a certain mass ratio is used as one type of soil to systematically discuss the similarities and differences of the mechanical behaviors of different soils,and to verify the applicability of the subloading surface concept more comprehensively.It can be seen from the calculation results that the model based on the concepts of superloading and subloading can also well describe the main mechanical behavior of the intermediate soil.

6.Conclusions

In this paper,a constitutive model based on the concepts of superloading and subloading is introduced to give a unified description of four soils.The “state dependence” is discussed,and the performance of the model is confirmed with drained triaxial tests.The work is expected to be applied to the numerical analyses on geotechnical engineering problems of complex soil profiles with different soils from sandy to clayey soils.The conclusions of the study are drawn as follows:

(1) The peak shear stress ratio in triaxial tests is dependent on the initial state of the soil,such as overconsolidation or compaction degree,and cannot be used as an inherent characteristic parameter of the soil.On the contrary,the residual shear stress ratio is not affected by the initial state of the soil and can be used as an inherent characteristic parameter of the soil.

(2) Unlike clayey soil,the inherent curve NCL(parameterseNand λ) of sandy soil is difficult to obtain directly from isotropic compression test.In practice,the parameterseNand λ of sandy soil with different initial void ratios can be determined indirectly according to a set of parallel curves similar to CSL.

(3) This study did not intend to focus on the mechanical properties of the intermediate soil.However,it is found that the mechanical behaviors of the intermediate soil are essentially similar to that of sandy soil and clayey soil,showing the general mechanical behaviors of granular geomaterials.On the other hand,mixing clayey particles in sandy soil will inevitably change its mechanical behaviors,causing a decrease in shear strength and making the compression behavior look more likely as a clayey soil.

(4) The similarities and differences of different soils are discussed uniformly.The model based on the concepts of superloading and subloading is confirmed to be a promising one,which has great potential for describing the general mechanical behaviors of different soils within a unified framework.This provides an important and effective way to determine the material parameters of different soils,which is often thought to be a bottleneck for engineers to use a sophisticated constitutive model in practical engineering.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

The financial support from the National Natural Science Foundation of China (Grant Nos.41727802 and 42072317),the Science and Technology Project from Construction System in Jiangsu Province,China (Grant No.2017ZD204),and ‘A Project’ funded by the Priority Academic Program Development of Jiangsu Higher Education Institutions,China,is highly appreciated.

Appendix A.Supplementary data

Supplementary data to this article can be found online at https://doi.org/10.1016/j.jrmge.2022.02.015.