基于SWMM模型的城市排水模拟应用研究
于永强 刘 培 程发顺
(中国电建集团中南勘测设计研究院有限公司规划研究院,长沙 410011)
0 引 言
研究区域谌家矶作为长江新城近期重点启动区,城市化进程不断加快,土地利用性质、市政管网建设将极大改变城市雨水排放格局,为保证谌家矶水安全保障体系健全和长江新城高标准建设,对区域雨水管网排水能力进行评估。本文评估模型选用SWMM 模型,其具有动态模拟降雨-径流的能力,广泛应用于城市单一降水时间的模拟。
由于城市化进程中将改变城市下垫面类型,造成径流系数的变化,继而影响城市排水防涝形势。近年来极端天气气候发生概率增大,降雨过程的不确定性也逐渐增大。在应用SWMM 模型(Storm Water Management Model)进行城市排水模拟中,径流系数变化会导致地表径流量变化,影响雨水管网负荷情况,而相同降雨强度和历时的降雨事件下,雨峰偏后普遍会导致排水压力增大。综合以上因素需要对不同径流系数和降雨过程对城市排水防涝形势造成的不确定性进行分析研究。
1 研究区域概况
研究区域谌家矶位于武汉市江岸区北部,长江新城西南部,北靠府寰河,南邻长江(图1)。规划建设用地面积12.4 km2,地处东经114°19′—114°23′,北纬30°39′—30°42′。属北亚热带季风性(湿润)气候,降雨量约为1 150~1 450 mm,降雨集中在每年6—8月,占全年降雨量40%左右。受季风和热带气旋影响,研究区域易遭受强降雨,同时由于地势平坦,排水动力不足,给城市排水系统带来较大压力,易形成积水内涝灾害。
该区域作为长江新城近期重点启动区,城市化进程较快,未来主要用地类型为居住和商业用地,因此区域硬化程度将增大。区域高程为22~35 m,坡度为0.12%~5.10%,地形地势较为平坦。研究区域内主要河流有朱家河、斗马河、四季渠和平安渠,是雨水管网的承泄水体。

图1 研究区域示意图
2 模型构建
2.1 设计暴雨
本次设计暴雨采用武汉市暴雨强度公式及设计暴雨雨型推求,暴雨强度公式见下式:

式中:P为重现期,根据《武汉长江新城起步区控制性详细规划》,本次P取5;t为降雨历时,根据管道汇流时间取2 h。
暴雨过程采用芝加哥雨型拟合,在设计重现期2~100 a内综合雨峰位置系数r取0.7。为研究雨峰位置系数对城市排水过程影响,本次雨峰位置系数r分别选用0.5、0.7和1.0进行对比分析,拟合得到的3条暴雨过程线见图2。
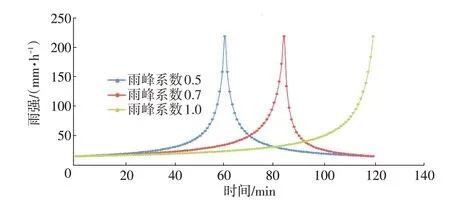
图2 不同雨峰位置系数的设计暴雨过程
径流系数与城市降雨产汇流密切相关,径流系数增大将显著增大地表径流量,进而影响城市排水防涝形势。依据下垫面现状和《室外排水设计标准》(GB 50014—2021),谌家矶的区域综合径流系数为0.55~0.65,考虑其作为长江新城近期重点启动区,城镇化发展潜力巨大,径流系数可能有较大增长,因此增设径流系数为0.75和1.00两个对比情景。当雨峰位置系数r为0.5时,设置径流系数为0.55、0.65、0.75和1.00共4个模拟情景,不同折减系数的设计暴雨过程见图3。

图3 不同折减系数的设计暴雨过程(雨峰位置系数r=0.5)
2.2 雨水井
雨水井构建主要依据研究区雨水管网CAD 成果,将CAD导入GIS平台处理后导入SWMM模型,构建雨水井对象共计1 110个,主要信息包含雨水井、雨水排口和管道的尺寸、位置和标高等,雨水井构建示意图见图4。
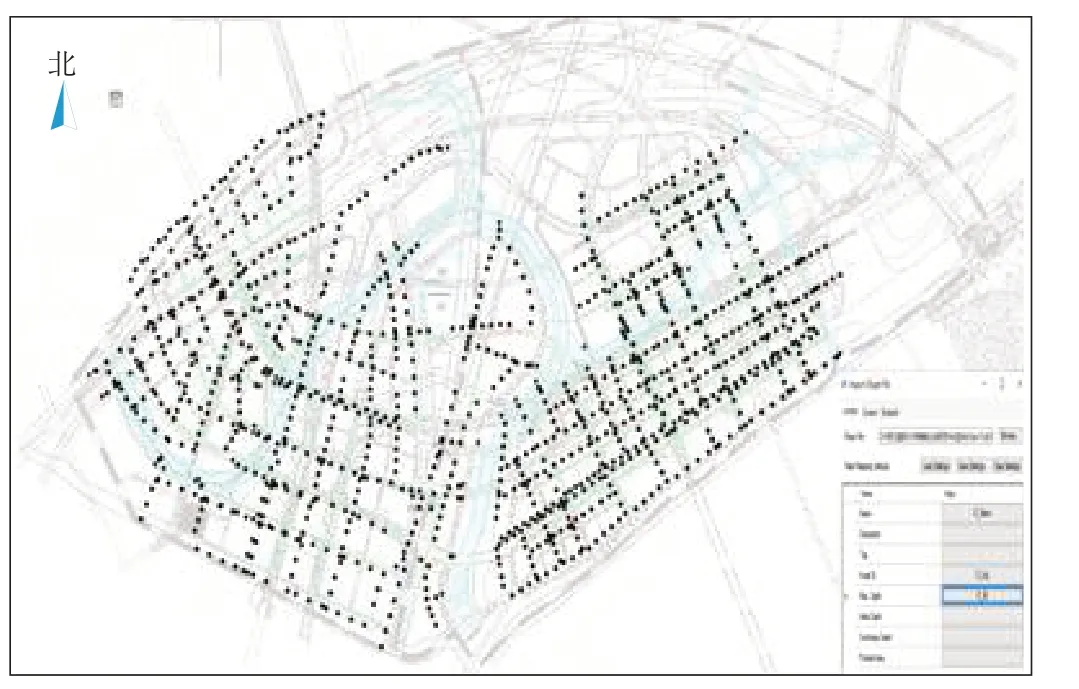
图4 雨水井构建示意图
2.3 雨水井
雨水管段构建主要依据研究区雨水管网CAD成果,将CAD导入GIS平台处理后导入SWMM模型,构建雨水管段共1 105 段,主要信息包含入流节点、出流节点、长度、糙率、出入口偏移等,雨水管渠构建示意图见图5。

图5 雨水管渠构建示意图
2.4 子汇水分区
子汇水分区的划分首先考虑规划的排水分区,根据排水分区划分为Y1、Y2、Y3和Y4 4个大分区,每个大分区内部再采用泰森多边形进行子汇水分区划分,共细分为1 110个子汇水分区见图6。

图6 子汇水分区示意图
子汇水分区主要参数为雨量计、出流节点、面积、漫流宽度、坡度、不透水率、不透水面积糙率等。其中漫流宽度是指子汇水面积与地表漫流最长路径长度的比值,在理想化的汇水分区模式图中,地表漫流沿不同路径经过的长度都一样。本次漫流宽度取值采用面积与漫流长度的比值。
本次产流计算采用径流系数法,具体下渗损失水量已在设计暴雨输入时考虑,因为SWMM 模型中不考虑下渗,所有子汇水分区的不透水面积占比为100%。
子汇水分区坡度取值大小将影响坡面汇流速率,不同子汇水分区的坡度根据区域内平均坡度取值。平均坡度采用GIS 坡度分析获取,谌家矶片区内地势较为平缓,各排水分区坡度为0.03%~5.50%。
2.5 参数选取及率定
本次产流计算采用径流系数法,不考虑Horton产流模型相关参数的率定,主要率定参数为曼宁系数、漫流宽度、坡度。通过研究区域的地形、用地类型和雨水管网资料,结合GIS的坡度坡向分析、叠加加权分析选取模型参数。
利用研究区域易涝区调查信息对城市排水模型进行率定,在2年一遇2 h设计暴雨情景下,易涝区分布与调查易涝区分布基本一致,模型率定情况见图7,模型参数率定结果见表1。

图7 模型率定情况图

表1 模型参数率定成果表
3 模拟计算
3.1 方案拟定
研究区域作为长江新城起步区,未来土地利用类型将发生较大变化,径流系数会相应发生一定变化。本次设计暴雨过程采用芝加哥雨型拟合,雨峰位置系数取值决定设计暴雨峰值出现时间,对模拟结果可能产生一定影响。综合以上因素,本文将考虑不同的雨峰位置系数和径流系数,进行敏感性分析,具体模拟方案如表2所示。
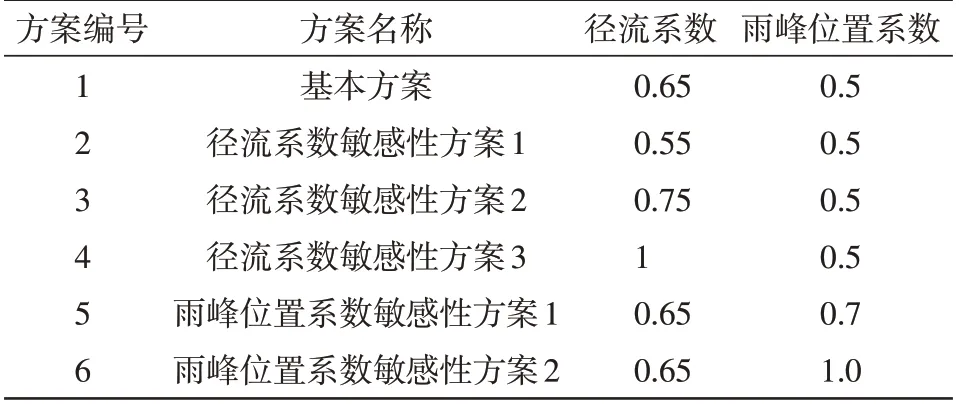
表2 研究方案表
3.2 结果分析
本次研究方案共6 组,方案1、2、3、4 为径流系数对比方案,方案1、5、6 为雨峰位置系数对比方案。模拟结果评价指标为溢流雨水井和超载管段数量,当雨水井发生超过1 h的溢流认为产生严重溢流;当发生满管流,管道流态由无压流转变为有压流时,认为管道发生超载,当管段有压流态下过流能力仍无法有效排除雨水来流时,认为发生严重超载。为评估不同因素对城市排水形势的影响程度大小,对评价指标敏感度进行归一化处理得到相对敏感度,相对敏感度计算公式如下。
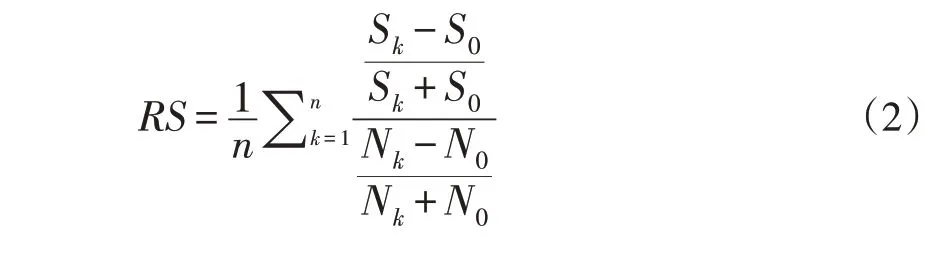
式中:RS为相对敏感度;Sk为第k个敏感性方案的模拟值;S0为基本方案的模拟值;Nk为敏感方案的模型参数值;N0为基本方案的模型参数值;n为敏感性方案数量。
3.2.1 径流系数
对模拟结果的溢流雨水井和超载管段进行统计,得到径流系数对比方案结果统计表和统计图,具体如表3、图8所示。

表3 径流系数对比方案结果表 %
径流系数由0.55增大到1.00过程中,积水井点占比由2.25%增加至10.37%,增加了8.12%;严重集水井占比由0.72%增加至2.52%,增加了1.80%;超载管道占比由10.01%增加至18.21%,增加了8.20%;严重超载管道占比由0.63%增加至2.52%,增加了1.89%。由上可知,随着径流系数增大,雨水管网系统负荷率逐渐增大,雨水井积水和管段超载情况逐渐增多。
3.2.2 雨峰位置系数
对模拟结果的溢流雨水井和超载管段进行统计,得到径流系数对比方案结果统计表和统计图,具体如表4、图9所示。

表4 雨峰位置系数对比方案结果表 %

图9 雨峰位置系数对比方案结果图
雨峰位置系数由0.5增大到1.0过程中,积水井点占比由5.12%增加至7.94%,增加了2.82%;严重集水井占比由0.84%增加至0.86%,增加了0.02%;超载管道占比由11.20%增加至13.31%,增加了2.11%;严重超载管道占比由1.17%增加至1.25%,增加了0.08%。由上可知,随着雨峰位置系数增大,雨水管网系统负荷率逐渐增大,雨水井积水和管段超载情况逐渐增多。
3.2.3 相对敏感度
本文排水模拟成果评价指标主要有积水井点、严重积水井点、超载管道和严重超载管道,根据相对敏感度计算公式可以得到不同对比方案、不同扰动程度下的相对敏感度,具体结果如表5所示。

表5 评价指标相对敏感度成果表
由上可知,在4项评价指标中,径流系数相对敏感度分别为3.04、2.63、1.21 和2.01,雨峰位置系数相对敏感度分别为0.41、0.01、0.21 和1.33,径流系数相对敏感度均大于雨峰位置系数相对敏感度,在城市排水模拟中径流系数相对于雨峰位置系数影响更大。
积水雨水井和严重积水雨水井的径流系数相对敏感度大于超载管段和严重超载管段的径流系数相对敏感度,可见径流系数对雨水井积水情况影响更大。超载管段和严重超载管段的雨峰位置系数相对敏感度大于积水雨水井和严重积水雨水井的雨峰位置系数相对敏感度,可见雨峰位置系数对管段超载情况影响更大。
其原因在于径流系数主要影响地表径流量,径流系数增大将导致地表径流峰值和径流总量增大,而内涝积水主要是由于多余涝水无法及时排除导致。雨峰位置系数主要影响暴雨峰值发生时刻,一般而言暴雨峰值约靠后,雨水管网最大过流量发生时的排水系统可用调蓄容积越少,发挥的“削峰”作用越弱。
4 结 论
(1)研究区域雨水管网标准不足5年一遇,当发生重现期5 a 及以上强度的暴雨时,将出现不同程度的雨水井溢流和管段超载,从而导致城市积水内涝。
(2)径流系数的相对敏感度显著大于雨峰位置系数相对敏感度,可见在城市排水模拟中径流系数相对于雨峰位置系数影响更大,应重点关注径流系数的合理取值。
(3)不同评价指标下的相对敏感度根据类别不同有明显差异,积水雨水井的径流系数相对敏感度大于超载管段的径流系数相对敏感度,超载管段的雨峰位置系数相对敏感度大于积水雨水井的雨峰位置系数相对敏感度。可见径流系数更侧重于影响地面积水,雨峰位置系数更侧重于影响管网排水,在管网排涝能力模拟评估时应考虑雨峰位置系数的影响。
——以长春市天安第一城海绵城市专项为例
——以武汉港西汇水系统为例

