A novel method for atomization energy prediction based on natural-parameter network

Choqin Chu ,Qinkun Xio,,∗∗ ,Chozheng He ,Chen Chen ,Lu Li ,Junyn Zho ,Jinzhou Zheng,Yinhun Zhng

a School of Mechanical and Electrical Engineering,Xi’an Technological University,Xi’an 710021,China

b School of Electrical and Information Engineering,Xi’an Technological University,Xi’an 710021,China

c School of Materials Science and Chemical Engineering,Xi’an Technological University,Xi’an 710021,China

Keywords:Structure prediction Atomization energy Deep learning Coulomb matrix NPN End-to-end

ABSTRACT Atomization energy (AE) is an important indicator for measuring material stability and reactivity,which refers to the energy change when a polyatomic molecule decomposes into its constituent atoms.Predicting AE based on the structural information of molecules has been a focus of researchers,but existing methods have limitations such as being time-consuming or requiring complex preprocessing and large amounts of training data.Deep learning (DL),a new branch of machine learning (ML),has shown promise in learning internal rules and hierarchical representations of sample data,making it a potential solution for AE prediction.To address this problem,we propose a natural-parameter network (NPN) approach for AE prediction.This method establishes a clearer statistical interpretation of the relationship between the network’s output and the given data.We use the Coulomb matrix (CM) method to represent each compound as a structural information matrix.Furthermore,we also designed an end-to-end predictive model.Experimental results demonstrate that our method achieves excellent performance on the QM7 and BC2P datasets,and the mean absolute error (MAE) obtained on the QM7 test set ranges from 0.2 kcal/mol to 3 kcal/mol.The optimal result of our method is approximately an order of magnitude higher than the accuracy of 3 kcal/mol in published works.Additionally,our approach significantly accelerates the prediction time.Overall,this study presents a promising approach to accelerate the process of predicting structures using DL,and provides a valuable contribution to the field of chemical energy prediction.

Accurate prediction of structures in chemical compound space(CCS) is crucial for the design and synthesis of novel materials[1].Although theoretical structure prediction methods have been widely adopted in material research [2,3],the computational cost associated with large-scale structural systems remains a challenge.A CALYPSO software based on swarm intelligence has been developed to accelerate structure prediction [4,5].The existing firstprinciples-based (DFT) methods are time-consuming and economically expensive when applied to predict large-scale structures.Consequently,there is an urgent need to accelerate the process of material structure prediction [6].

Typically,structure prediction methods involve several steps[6]: (1) Randomly generating an initial population of structures under symmetry constraints;(2) Assessing the similarity among generated structures and eliminating duplicates;(3) Performing local optimization and energy calculations using the DFT on generated structures;(4) Constructing the next generation of structures using swarm intelligence algorithms,where low-energy structures evolve into new structures while high-energy structures are replaced by randomly generated ones.However,for large-scale structures containing hundreds or thousands of atoms,the computational time required for energy calculations is significant.Furthermore,performing energy calculations and optimizations for multiple randomly generated structures further compounds the time cost.This limitation significantly impedes the prediction of large-scale material structures in most structure prediction software.Deep learning(DL) methods have gained substantial success in computer vision,pattern recognition,and other fields [7,8].However,their application in predicting and generating new structures in computational chemistry remains limited [9].

In conclusion,the acceleration of material structure prediction is a critical problem that needs to be addressed.While traditional methods face challenges in dealing with large-scale structures,DL methods offer a potential solution.By leveraging DL techniques,it may be possible to overcome the time constraints associated with energy calculations and optimize the prediction process.This application of DL in computational chemistry holds promise for advancing the field of structure prediction and generating new structures.

In recent years,the rapid development of artificial intelligence has made ML a new method that researchers are eager to explore.ML has become popular in various application scenarios that require prediction,classification,and decision-making [4,10].With the availability of large-scale quantum mechanical data [11–13],researchers have established ML models and used them to predict material properties such as formation energies,defect energies,elasticity,and other mechanical properties [4].For instance,Hansenetal.[14] employed a linear regression (LR) algorithm to learn the relationship between structural information and cluster energy and predicted the energy of new clusters based on atomic Cartesian coordinates and nuclear charge.Meanwhile,neural network (NN) methods [15,16] have been leveraged to accelerate the construction of potential energy surfaces.Ruppetal.[17] introduced a machine learning model that predicts the AEs of different organic molecules.Guptaetal.[18,19] utilized the DL method to establish the correlation between molecular topological features and accurate AE predictions,achieving an impressive MAE.

In addition,some DL methods were used to replace the DFT calculation process to reduce the computational complexity of the system and accelerate structure prediction in an end-to-end way[20].Due to the strong feature extraction and feature learning abilities of the DL methods,we have introduced a new NPN [21] model that predicts the AE of different molecules in an end-to-end manner based solely on nuclear charge and atomic position.To address this task,an end-to-end energy prediction model was constructed,and its schematic diagram is shown in Fig.1.

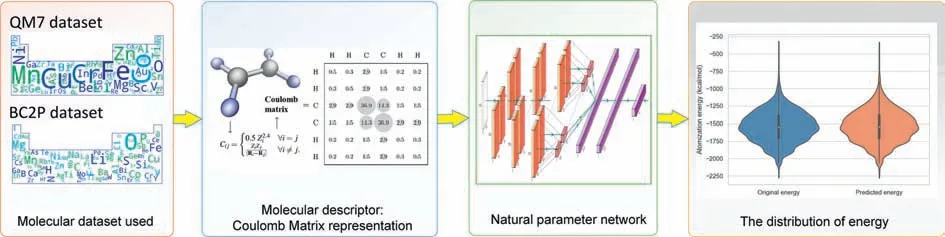
Fig.1. Schematic diagram of an end-to-end chemical energy prediction process.

LetΦbe an AE prediction model,and the modelΦNPNutilizes a neural network architecture for probabilistic modeling.The model leverages the properties of exponential family distributions to transform the neural network output into the natural parameters of the exponential family distribution.This allows NPN to conveniently parameterize the probabilistic model and maximize the log-likelihood function using gradient-based optimization algorithms during training.NPN transforms the conditional probabilityp(Y/X) between the input variable and the output variable into the form of an exponential family distribution.According to all the molecular structure information,we extract the coordinate information of all atoms of each molecule as the input ofΦNPN,which is represented by X.The AE of each molecule is represented by Y.Here we have:

where X is the coordinate information of all atoms of each molecule,andθNPNis the parameters of the NPN model.NPN consists of both linear and nonlinear transformation layers.Here,we first introduce the linear form of NPN.For simplicity,let’s assume a Gaussian distributionξ=(q,d)Twith two natural parameters.We decompose the distribution over a weight matrix=is the corresponding natural parameter.We assume similar decomposed distributions forbl,zl,andxlin NPN,which are all exponential family distributions.For computational convenience,we wish to approximatezlusing another exponential family distribution by matching its mean and variance.To computeandwe can obtainfrom the meanand varianceofzlas follows:

where,the symbol ⊙represents the product of the elements in a distribution,while the bijective functionf(.,.) maps its natural parameters to the distribution’s mean and variance.Similarly,symbolf−1(.,.) denotes the inverse transformation.The means and variances ofWlandbl,which are obtained from the natural parameters,are represented byrespectively.The values ofthat are computed can be used to recoverthereby streamlining the feed-forward calculation of the nonlinear transformation.

Once we have the distribution overzl,defined by natural parametersthat has been linearly transformed,we then apply an element-wise,nonlinear transformationv(·) to it.The resulting distribution of activations is denoted aspx(xl)=pz(v−1(xl))|v−1＇(xl)|,wherepzis the factorized distribution overzldefined by.Even ifpx(xl) is not an exponential-family distribution,we can still approximate it usingby matching the first two moments.Once we obtain the meanand varianceofpx(xl),we can compute the corresponding natural parameters usingf−1(.,.).The feed-forward computation can be expressed as:

To model distributions over weights and neurons,the natural parameters must be learned.The NPN is designed to take a vector random distribution as input,such as a multivariate Gaussian distribution.It then multiplies this input by a matrix random distribution and applies a nonlinear transformation before outputting another distribution.Since all three distributions in this process can be characterized by their natural parameters,learning and prediction of the network can be performed in the space of natural parameters.During back-propagation,for distributions characterized by two natural parameters,the gradient is composed of two terms.For instance,in the equation∂E/∂zq=(∂E/∂xm)⊙(∂xm/∂zc)+(∂E/∂xs)⊙(∂xs/∂zq),whereErepresents the error term of the network.Naturally,nonlinear NPN layers can be stacked to form deep NPN,as shown in Algorithm 1.NPN does not need expensive reasoning algorithms,such as variational reasoning or Markov chain Monte Carlo (MCMC).Moreover,in terms of flexibility,it can choose different types of exponential family distributions for weights and neurons.

Algorithm 1 Deep NPN’s algorithm.

We know thatχcan be converted using a previous study[22] with Coulomb matrices (CM).The CM are matrices that contain information about the atomic charges and atomic coordinates.The CM can be calculated using the following formula:

among them,1 ≤i,j≤23,Ziis the nuclear charge of atomi,andRiis its Cartesian coordinate.

Specifically,QM7 is a dataset consisting of 7165 molecules taken from the larger GDB-13 database,which comprises nearly one billion synthetic organic molecules.QM7 has information about the molecule that consists of the atoms H,C,N,O,and S.The maximum number of atoms in a molecule is 23.The molecules in QM7 exhibit a diverse range of chemical structures,such as double and triple bonds,cycles,carboxylic acids,cyanides,amides,alcohols,and epoxides [23].The CM representation is used to describe the molecular structures,and this approach is invariant to translations and rotations of the molecule.In addition to the CM,the dataset includes AEs ranging from −800 kcal/mol to−2000 kcal/mol [14].

The main focus of this article is on theχandLcomponents in the QM7 dataset.Due to the varying number of atoms in each molecule,the sizes of their true CMs are also different.To make all CMs with the same size of 23×23,we extended the size of the original CM and filled the expanded space in the CM with 0.

For NPN,GCN,CNN,and LSTM models,we use the rectified linear unit (ReLU) activation function in the hidden layer.We used the ADAM optimizer [24] with a learning rate of 0.0001 and a decay rate of 0.00001,and based on our experience and knowledge,we have selected different combinations of network hyperparameters for model training and fine-tuning.We set the learning rate to [0.01 0.001 0.0001],the number of training rounds[100 200 300],the batch size [32 64 128],and the hidden layer nodes [100 200 300].Then,we combined the values of different network hyper-parameters.The experimental results showed that when the learning rate was 0.0001,the batch size was 64,the hidden layer nodes were 200,and the number of training rounds was 200,the model performance was optimal.The proposed models have been implemented in the Pytorch library.As for the hardware system configuration,the processor is an Intel (R) Xeon (R)Silver 4110 CPU@2.10 GHz,the RAM has a capacity of 32.0 GB,and the graphics card is an NVIDIA RTX 2080 Ti [25].We randomly divided the dataset into a training dataset and a test dataset in the ratio of 8:2.

We used the proposed method to train the AE prediction models on training data and validated the performance of the models using testing data,and the losses of the proposed models during the training are shown in Fig.2.

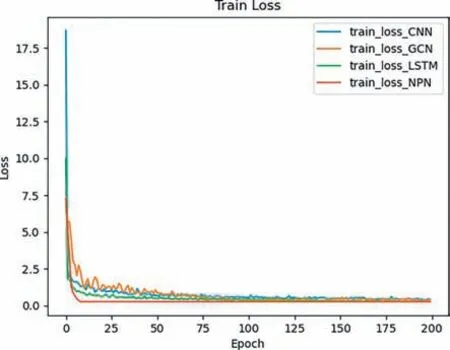
Fig.2. The results of training losses of different DL models.

By training on a large set of different molecules in QM7,we use MAE and root mean square error (RMSE) as evaluation indicators to evaluate the prediction performance of various algorithms under different molecule presentation methods.The comparison results between our method and other methods [22] are shown in Table 1.Our results indicate that the proposed method exhibits a lower prediction error,indicating excellent prediction performance.Based on this,we trained and tested different DL models we designed on the QM7 dataset [26],and obtained some information that reflects the performance of the models,such as model parameters,testing time,and testing errors.Experiments on real-world datasets [26] show that NPN can achieve state-of-the-art performance on regression tasks.The performance of different methods are compared in Table 2.

Table 1 Comparison of prediction errors across multiple algorithms under different representation types using MAE and RMSE metrics.

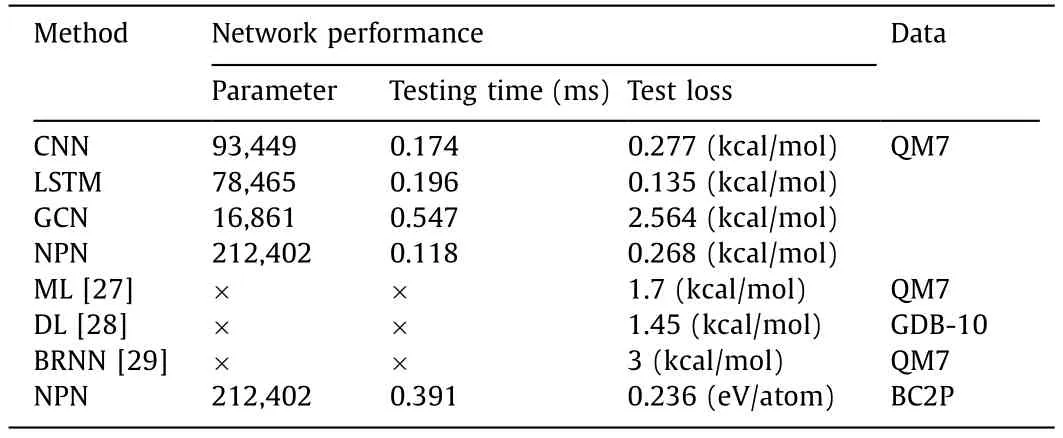
Table 2 Comparison results of performance evaluation of different networks.

In previous experiments [14],researchers often merged feature values/vectors and feature centers with flattened CM to form a 7165-sample dataset withN-dimensional features.However,the integration of new molecular property information has brought about a new problem: the concatenation of old and new features may lead to unwanted “heterogeneity” in the feature vectors,and including more features may actually increase noise in the dataset[30].It should be noted that some traditional ML techniques may not be able to identify meaningful patterns from these newly added features,so merging new features may result in poorer results [31].

We present the results analysis of AEs prediction for four different molecules and their isomers,it can be shown in Fig.3.Based on the structural information,our proposed method achieved good AE prediction results by using the extended CM method to characterize molecules.However,we also found that the model has a significant prediction error for molecules [32] with fewer atoms,which may be due to the interference of additional information supplemented in the extended CM to the model’s learning of structural information features.For some molecules with compact structures relative to sparse spatial structures,the prediction errors were relatively larger.We analyzed that this may be due to the high density distribution of a large number of identical atoms in the molecule,which led to the model’s unsatisfactory extraction of the CM features.

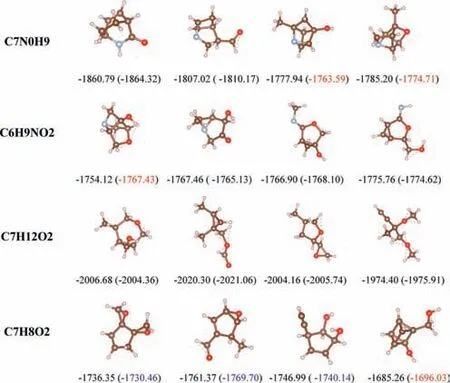
Fig.3. Visualization of different conformations of four molecules and comparison of their AE prediction results.Corresponding predicted AEs by our model are shown in parentheses,all AEs are in kcal/mol.Our model has a prediction error of about 0.2–3 kcal/mol for AE.The data marked in blue indicates an error between 5 and 10 kcal/mol,while the data marked in red indicates an error over 10 kcal/mol.

To validate the robustness and effectiveness of our proposed method,we randomly divided the BC2P data from Fuetal.[33] into a train dataset and a test dataset with an 8:2 ratio.We use our proposed method to train a model on train data,and the trained model accurately predicts the corresponding energy [33].The training loss curve can be seen in Fig.4.Moreover,we tested the model on test data,and the results showed that our model had an average prediction time of 0.391 ms for the energy of each molecular conformation and an average test loss of 0.236 eV/atom.The results of performance evaluation of NPN model on BC2P is shown in Table 2.

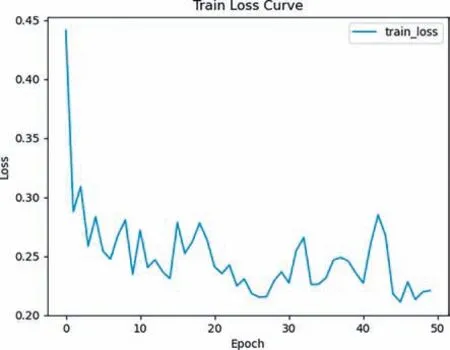
Fig.4. The results of training loss curve of our model on BC2P data.

The study aims to propose and validate a method for predicting atomic energy.Initially,we introduce the extended CM representation of molecular structure along with its inherent characteristics.Subsequently,we compare the performance of various ML and DL models for predicting AEs.These models not only enable fast AE prediction but also expedite the structure prediction process.Furthermore,to overcome the limitations of our current method,we plan to incorporate the three-dimensional spatial pattern of material structure information in future research.We intend to employ the graph convolutional network (GCN) method to mathematically represent atoms in chemical molecules.In addition to model development,we informally discuss the results of numerical experiments conducted in this study.Through extensive comparative experiments and analyses,we gain valuable insights into the performance and potential applications of the proposed method.Some potential applications include catalyst design,materials discovery,optimization of energy storage and conversion,as well as material performance prediction.In the future,we envision conducting further in-depth research on material performance prediction and material discovery.By leveraging the power of machine learning and data mining techniques on large datasets,we can uncover hidden correlations within complex data structures.This will allow us to predict new material structures and their corresponding properties.Ultimately,this research contributes to the advancement of materials science and opens up new possibilities for designing innovative materials with tailored properties.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgment

This work was supported by the Nature Science Foundation of China (Nos.61671362 and 62071366).