多模态混合输入模拟实验过程实现新型Al-Si-Mg 系合金设计*
段志强 裴小龙 郭庆伟 侯华 赵宇宏†
1) (中北大学材料科学与工程学院,太原 030051)
2) (山西省有色金属液态成型工程技术研究中心,太原 030051)
3) (太原科技大学材料科学与工程学院,太原 030024)
数据驱动下,基于大量的实验数据,建立混合特征与力学性能之间非线性规律实现合金新成分的配比和工艺设计一直是一个挑战.本文基于机器学习的方法,提出一种面向性能的Al-Si-Mg 系合金“成分-工艺-性能”的设计策略.将同一体系不同牌号合金的成分、熔炼及热处理工艺等混合因素作为特征,通过随机森林寻找特征与抗拉强度之间的非线性规律.之后将数据集中部分合金的成分、工艺参数设置为目标空值,使用链式方程多重插补算法对目标缺失数据进行预测插补.通过该策略进行性能预测或指导设计的合金抗拉强度的实验值和预测值的误差均保持在±5%之内;而且经实验证实,其中Al-6.8Si-0.6Mg-0.05Sr 的成分配比和540 ℃×10 h+170 ℃×10 h 工艺方案使合金综合拉伸性能优异,质量指数QDJR 达到517.3,高于同类合金低于500QDJR 值的水平.这一结果表明该策略有助于改善高强度Al-Si-Mg 系合金传统设计方法周期长、成本高、效率低的问题.
1 引言
凭借高强度(150—400 MPa)、耐腐蚀和可铸性好的特点,Al-Si-Mg 系合金被广泛应用于传统制造行业.在Al-Si-Mg 系合金的生产过程中,影响合金最终性能的因素很多.基于传统试错实验来提升合金性能的方法主要包括改善合金成分[1−5],优化熔炼[6]和热处理工艺[7,8],以及制备金属基复合材料[9,10]等.然而这些基于传统试错实验的方法在设计新合金时存在周期长、成本高的问题.近年来,随着材料基因组计划的提出和发展[11,12],材料研发开始由经验试错模式向基于知识驱动、数据驱动下的大数据分析-设计-预测的模式革新[13,14].
数据驱动的金属材料“成分-工艺-性能”的研究取得了显著的进展,尤其是在钢材料和轻合金的研究中得到广泛应用.Wang 等[15]从马氏体钢的成分、热处理工艺等19 个参数中筛选出7 个作为输入,屈服强度和延伸率作为输出,使用随机森林算法得到能够提升马氏体钢屈服强度和延伸率的有效成分(Cr 的质量分数为8%—9%)和工艺(回火温度(755±5) ℃,回火时间30—120 min).Guo 等[16]通过筛选得到63127 个钢的数据样本,以Cu,Fe,S 等成分和退火温度等参数作为输入,屈服强度、抗拉强度和伸长率作为输出,基于随机森林设计出满足性能指标的成分和工艺(质量分数为1%的C,屈服强度(YS)=600 MPa,屈服强度/抗拉强度(TS)=0.8).同样将合金成分、工艺作为输入,性能指标作为输出,建立机器学习预测模型在铝、镁轻合金领域也得到较多的应用.对于加工生产普遍应用的AZ31 变形镁合金,Liu 等[17]基于实验数据使用人工神经网络算法建立AZ31 退火工艺(退火温度、退火时间)与抗拉强度、屈服强度、延伸率间的预测模型,最终通过全排列训练优化得到模型的平均相关系数为0.89,平均误差下降了2.91%;Xu等[18]则使用人工神经网络和支持向量机建立AZ31 合金成分(Zn,Al,Ca 等)、工艺参数(均匀化温度、挤压比、轧制温度、轧制比等)与抗拉强度、屈服强度、延伸率之间的定量关系,并制造一种新的AZ31 合金(Mg-0.7489Zn-2.998Al).在铝合金中,Chaudry 等[19]基于文献中的实验数据使用梯度提升树算法搭建关于铝合金成分(Al-Cu-Mg-x(x=Zn,Zr 等))-时效工艺-硬度之间的非线性预测模型,并对Al-4Cu-0.5Mg-0.15Si-0.1Sc 合金在175 和225 ℃时效的性能进行准确预测,其均方误差仅为7.27,决定系数达到0.94.
但是,由于数据量不足以及特征选择较片面,现有的研究对于Al-Si-Mg 系合金的设计仍存在局限性.其中,Yang 等[20]以固溶时效温度和时间4 种因素作为输入使用人工神经网络对A357 合金的抗拉强度和伸长率进行了预测,实验值与预测值的平均绝对误差分别为0.7%和1.85%,并通过等值线图找到了抗拉强度和伸长率之间的关系.Yi 等[21]使用A356-xSr 合金的计算热力学数据(相变温度、相分数、热扩散率、热导率、成核指数等)来预测合金的抗拉强度、屈服强度和延伸率,并通过分析合金的凝固行为建立“成分-凝固组织”之间的非线性联系得到该合金使用Sr 变质的最佳质量分数为0.005%.但是,影响合金最终性能的因素有很多,仅选取部分因素来研究其对性能的影响会在实际应用过程中受到限制.因此,有必要将上述研究过程中所使用到的这些特定的影响因素(合金的成分、热处理工艺等)以及目前研究过程中未使用到的影响因素(模具温度、浇注温度)整合到一起,使用一个特征全面、高质量的数据集通过机器学习来模拟整个实验过程,指导设计可以满足性能需求的合金.
本研究提出一种可以同时满足Al-Si-Mg 系合金成分、工艺设计和性能预测的机器学习策略.为了获得特征全面、数据分布均匀和“噪声”数据少的高质量数据集,收集了关于Al-Si-Mg 系合金相关文献的实验数据构成了由文本数据和数值数据组成的多模态数据集.将实验过程中涉及的合金成分、熔炼工艺及热处理工艺等因素作为输入特征,抗拉强度作为输出,通过构建随机森林和多重插补回归模型实现新合金的设计及其性能预测.最后经过实验进行验证,基于该策略我们可以设计出满足预期(345 MPa)抗拉强度达到349 MPa 的合金成分及热处理工艺,优于同类合金使用Sr 变质[22](Al-7.069Si-0.676Mg-0.02Sr) 341.8 MPa、Sc 变质[3](Al-7Si-0.6Mg-0.12Sc) 324 MPa和复合稀土Re变质[5](Al-6.75Si-0.63Mg-0.2Re)获得349.1 MPa的结果.
2 方 法
本研究提出一种针对Al-Si-Mg 系合金“成分(Al,Si,Mg,Ti,Sr 等)-工艺(模具类型、模具温度、变质温度、浇注温度、固溶和时效工艺)-性能(抗拉强度)”设计及预测的新策略,具体研究框架如图1所示.该策略主要包含数据收集、数据处理、特征筛选、模型构建、基于链式方程多重插补方法的合金设计和工艺设计、基于随机森林算法的性能预测、实验验证.
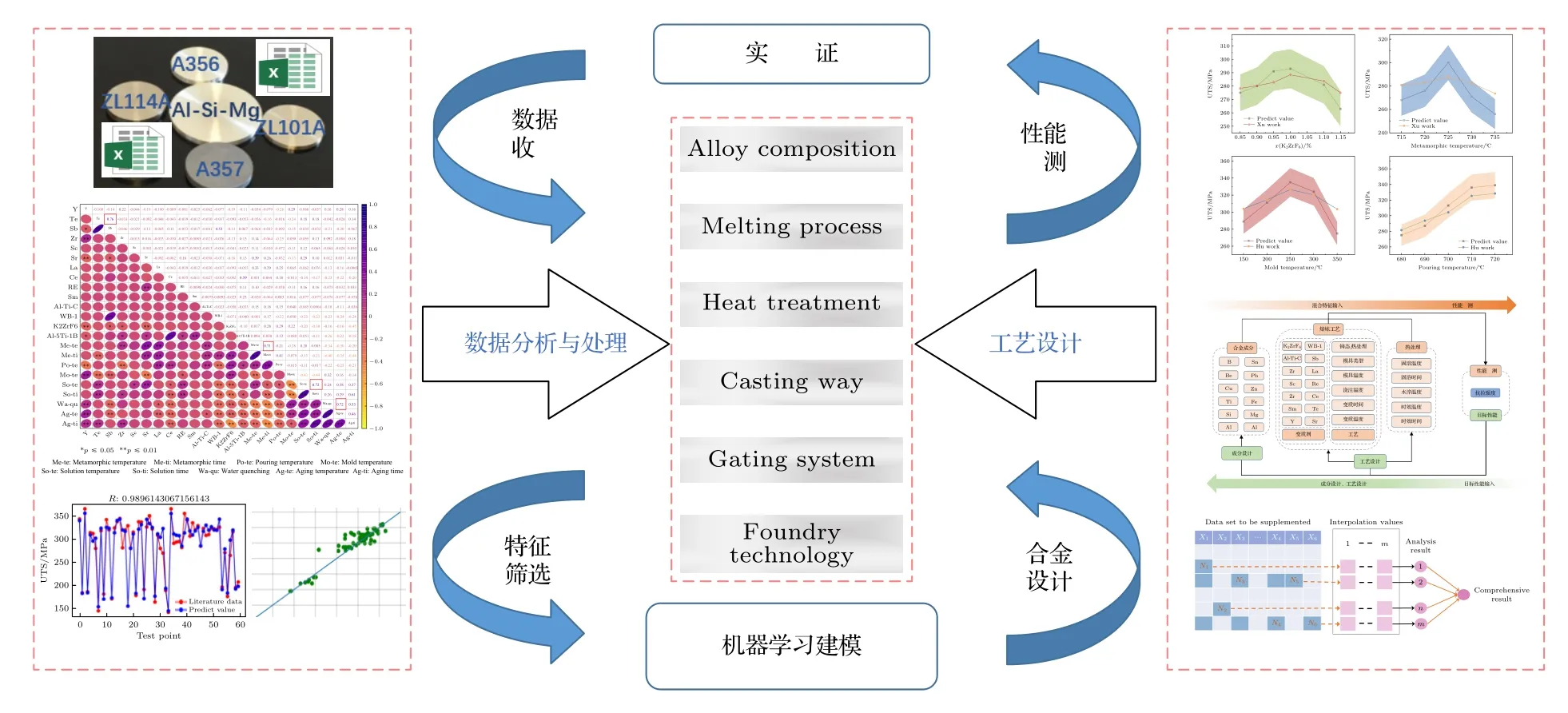
图1 Al-Si-Mg 系合金设计示意图Fig.1.Schematic diagram of Al-Si-Mg alloys design.
2.1 数据收集
一个可以高效表达输入与输出之间非线性规律的机器学习模型不仅要有足够的数据量,更需要保证数据的质量.因此,本工作收集了从2010 年至今所有关于A356,A357,ZL101A,ZL114A 牌号的实验数据,并选择实验过程中可以影响抗拉强度的37 个因素作为输入特征,如图2 所示.其中合金成分主要包括Al,Mg,Si 等基体元素;变质元素则是熔炼过程中常用到的Sr,Zr 等元素或稀土Y,Sc 等;熔炼工艺主要涉及模具类型、模具温度、变质温度等;热处理工艺主要包含了T6 热处理工艺的相关内容.
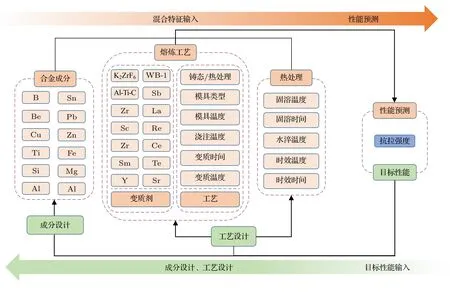
图2 Al-Si-Mg 合金“成分-工艺-性能”双向设计示意图Fig.2.Schematic diagram of bidirectional prediction of Al-Si-Mg alloy composition-process-property.
2.2 数据分析与预处理
2.2.1 多模态数据集的建立及数据预处理
生活中可以通过视听等感官收集不同来源的信息,在大脑中对这些多模态的信息进行理解、记忆并做出相应的反应.在机器学习中,多模态数据主要是数据集中包含多种数据类型,其中包括数字、文字、语音、图片、视频等.由于多模态数据间相互补充和相互关联的关系的存在,使得模型能够提取更多的特征并进行更大范围的预测,从而获得比单一数据模态模型更加可靠的预测结果.因此在本模型中,将模具类型(金属型、砂型)、后处理(铸态、热处理态)等文本分类描述性数据与传统的数字类型数据结合共同构成本模型所使用的多模态数据集.
在多模态数据集中文本特征不能直接作为机器学习模型的输入,必须进行数字化处理.因此选用one-hot 方法[23]对文本数据进行编码,即使用n位状态寄存器对n个特征进行编码,将分类变量作为二进制向量使用,将类别字段映射成整数值,并与原数据集中的数值字段拼接成完整的数据集.
在数据集中不同字段的量纲或规模比例是完全不一样的,从而导致特征值之间的差异较大,不利于样本处理.因此对数据进行了标准化处理[24].转换公式如下:
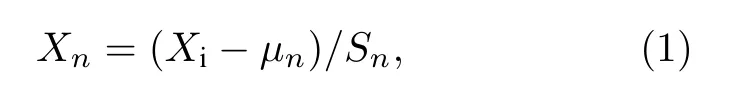
式中,µn为所有样本数据的均值,Sn为所有样本数据的标准差,Xi为原数据,Xn为现数据.
2.2.2 特征筛选
为避免输入特征中存在的冗余特征对模型计算造成负担,有必要通过特征相关性分析对高关联性特征进行筛选剔除.相关系数矩阵图可以直观表达出输入特征数据之间的相关关系.由于本研究的输入特征数值之间差异较大且不满足正态分布的情况,因此选用对原始数据要求较低的斯皮尔曼相关系数进行特征筛选[25].斯皮尔曼相关性分析是假设两个具有相同元素个数N的随机变量分别为X和Y,随机取第i (1≤i≤N)个值分别用Xi,Yi表示.对X,Y进行排序得到两个元素排行集合x,y,其中元素xi,yi分别为Xi在X中的排行以及Yi在Y中的排行.将集合x,y中的元素对应相减得到一个排行差分集合d,其中di=xi–yi,1 ≤i≤N.随机变量X,Y之间的斯皮尔曼相关系数可以由d计算得到[26],其计算方式为
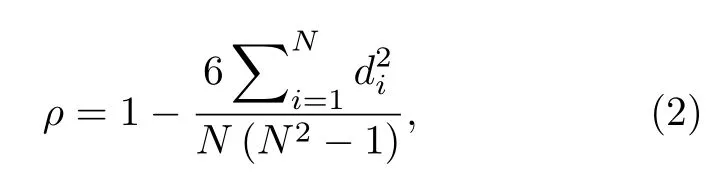
式中,ρ为斯皮尔曼相关相关系数,di表示顺序的差值,N表示数据个数.
2.3 模型构建
随机森林是一种为了满足预测需求集成多个相同类型决策树算法的集成机器学习.随机森林的预测结果依赖于其中的每一个决策树算法,是所有决策树算法预测结果的平均值,所以随机森林比单个决策树得到的结果更加准确[27,28].由于随机森林对数据集中的噪声不敏感,其更偏向于处理特征和输出之间复杂的非线性关系[15,16].因此在本研究中主要采用随机森林算法来建立模型,并将建立线性回归模型作为对照.训练前按4∶1 将数据集分为训练集和测试集,为进一步衡量模型对未知样本预测效果,选用决定性系数R来评估模型准确性,其定义为
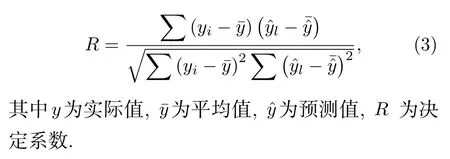
基于链式方程的多重插补方法最初由van Buuren 等[29]提出并应用于关于老年人生存影响的研究当中,之后在关于解决高空中电波传播数据缺失[30]以及电网电能量数据缺失[31]等计算物理领域的问题中有较好的表现.
多重插补算法主要是通过确定被插补变量与协变量的条件分布,来对缺失数据进行补充的一种方法[32].实际上是由一系列回归模型组成,即将数据集中具有缺失值的各个变量作为回归算法中的因变量,将其他剩余变量作为预测变量,依次拟合每个回归模型来对缺失的数据进行回归预测,其主要原理如图3 所示.其中X表示数据集的属性数量,Xj(j=1,2,3,···,s)表示第j个属性的名称,深蓝色方框表示缺失值,浅蓝色方框表示现有值,m表示填充次数.
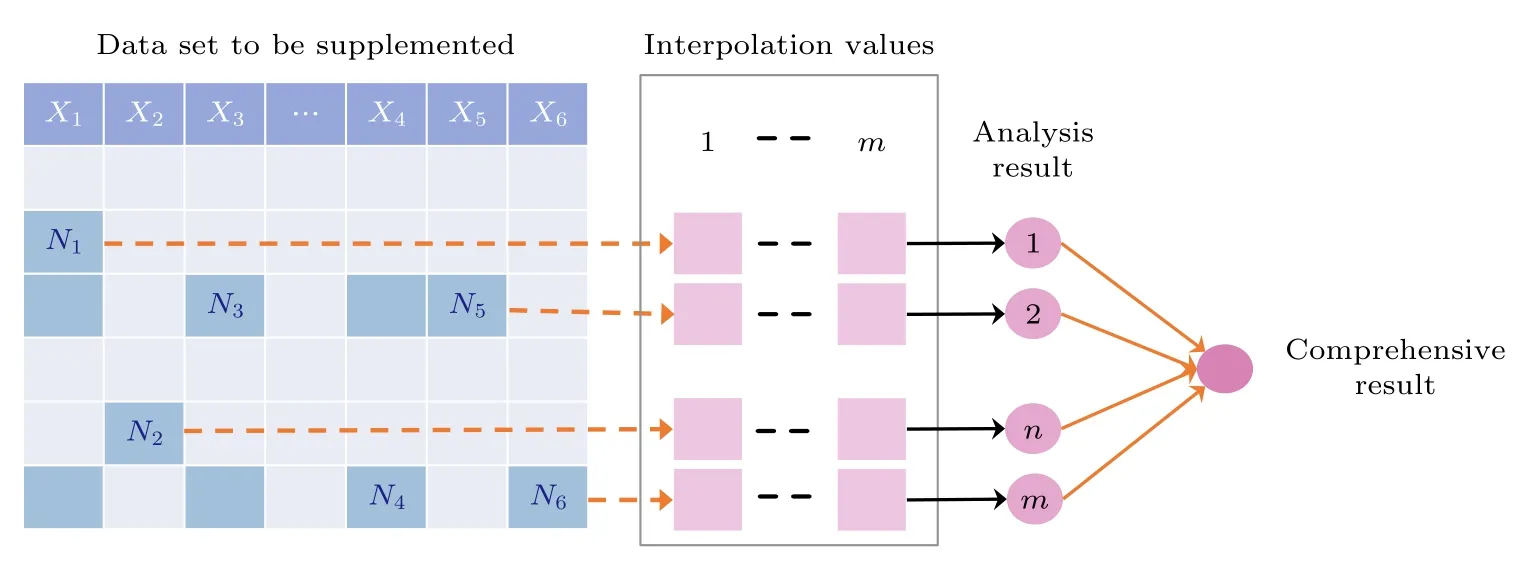
图3 链式方程多重插补示意图Fig.3.Schematic diagram of chain equation multiple imputation.
假设数据集有N个变量,如果N3为缺少值,那么它将在其他变量N1,N2,N4到Nk上回归.然后,将N3中的缺失值替换为获得的预测值.针对同一个数据集,在多重插补法主要为每一个缺失值同时构造m个插补值(m>1),这样就会生成m个数据集,对每个数据集使用相同的方法进行处理,得到m个结果,对来自各个插补数据集的结果进行整合,产生最终的统计推断.
3 合金制备与性能测试
实验前将各金属器具、坩埚置于干燥箱中200 ℃恒温干燥5 h,金属模具预热至200 ℃,所有接触的铁质器具均在表面喷涂涂料.实验过程依次采用Al-5Ti-B 进行细化处理、Al-10Sr 进行变质处理.
室温拉伸实验采用厚度为2.5 mm 的拉伸片(参考GB/T 228.1—2010 标准),采用AG-X plus电子万能试验机进行拉伸实验,取3 个试样的平均值作为最终测试结果.
4 结果
4.1 特征筛选及模型预测精度
通过斯皮尔曼相关性分析得到除合金成分外24 个输入特征两两之间的关系(合金成分属于必要的输入特征),如图4 所示.图中斯皮尔曼相关系数的正负代表正相关或负相关.数值大小代表相关程度,数值越接近于1 代表两参量之间的正相关度越高,将中度相关等级±0.75 视为阈值[33].如果两输入特征之间的相关系数绝对值大于0.75 时,则说明两输入特征之间的关联程度较高,需要剔除高相关性的特征.如图4 所示,根据计算共获得一组包含两个超过阈值的特征: Sn 和Te,因此,在指导设计实验时对于变质剂的选择Sn 和Te 仅需保留其中一个.同时存在部分特征系数接近阈值,其主要集中在在热处理工艺附近,例如固溶温度和水淬温度二者系数达到0.72,在此称其为强相关性特征.当我们需要进一步优化模型时,我们可以选择对部分强相关性特征进行二次筛选来提高整个模型的效率.
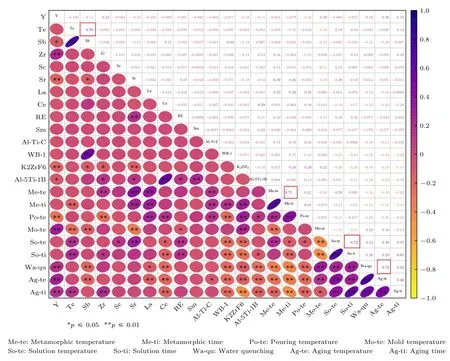
图4 斯皮尔曼相关系数矩阵图.紫色代表正相关,黄色代表负相关;椭圆越扁,数值越大;*号为显著性标记,根据显著性水平变化进行设置,小于0.05 和小于0.01 分别显示*和**Fig.4.Spearman correlation coefficient matrix plot.Purple represents a positive correlation,and yellow represents a negative correlation;the flatter the ellipse,the larger the value;the * sign is a significant mark,which is set according to the change of the significance level,and it is displayed as * and ** when it is less than 0.05 and less than 0.01.
筛选确定了模型的输入特征后,对随机森林和线性回归两种模型的泛化能力进行测试,并得到训练集和测试集的预测精度,如图5(a),(b)所示,随机森林训练集和测试集的决定系数分别为0.989和0.92,图5(c),(d)则是线性回归训练集和测试集的决定系数,分别为0.92 和0.79.通过对比两种模型的结果,可以发现随机森林模型的拟合程度几乎与y=x重合,其预测结果非常接近实际值,同时也证实随机森林的预测效果优于线性回归.

图5 随机森林算法泛化能力测试结果 (a)随机森林模型训练集的预测精度;(b)随机森林模型测试集的预测精度;(c)线性回归模型训练集的预测精度;(d)线性回归模型测试集的预测精度Fig.5.Random forest algorithm generalization ability test results: (a) The prediction accuracy of the random forest model training set;(b) the prediction accuracy of the random forest model test set;(c) the prediction accuracy of the linear regression model training set;(d) the prediction accuracy of the linear regression model test set.
4.2 成分和工艺设计
在进行合金成分及工艺的设计时,将合金目标性能作为特征输入,将要预测的合金的成分或相关工艺参数在数据集中设置为空值并作为输出,之后通过链式方程多重插补对数据集中缺失的成分或工艺参数进行多次回归插补,生成多组数据结果指导实验设计如表1 所示并对其进行实验验证得到图6 所示结果.
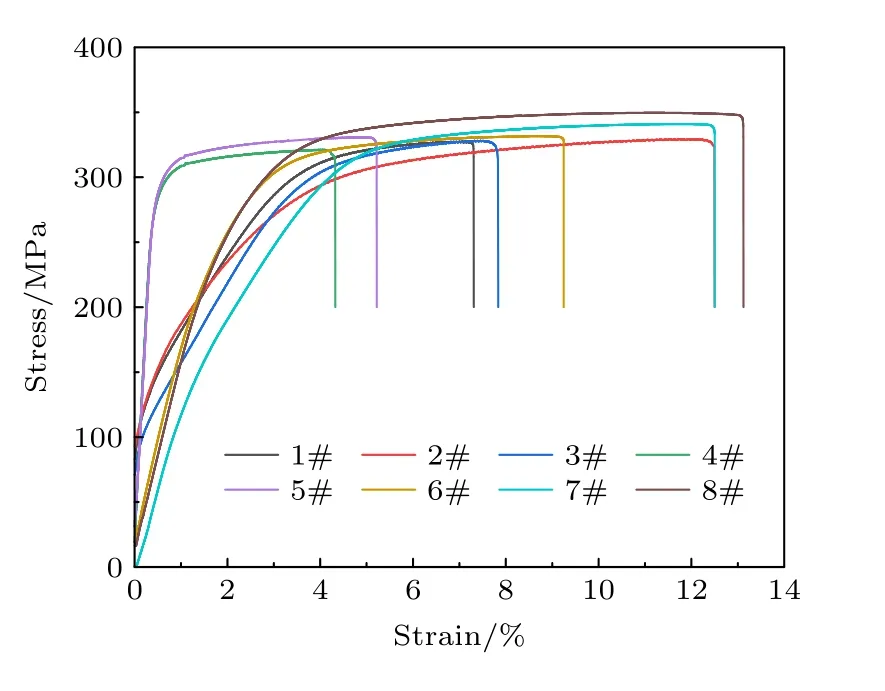
图6 新合金的成分及工艺的实验结果Fig.6.Experimental results of the composition and process of the new alloy.
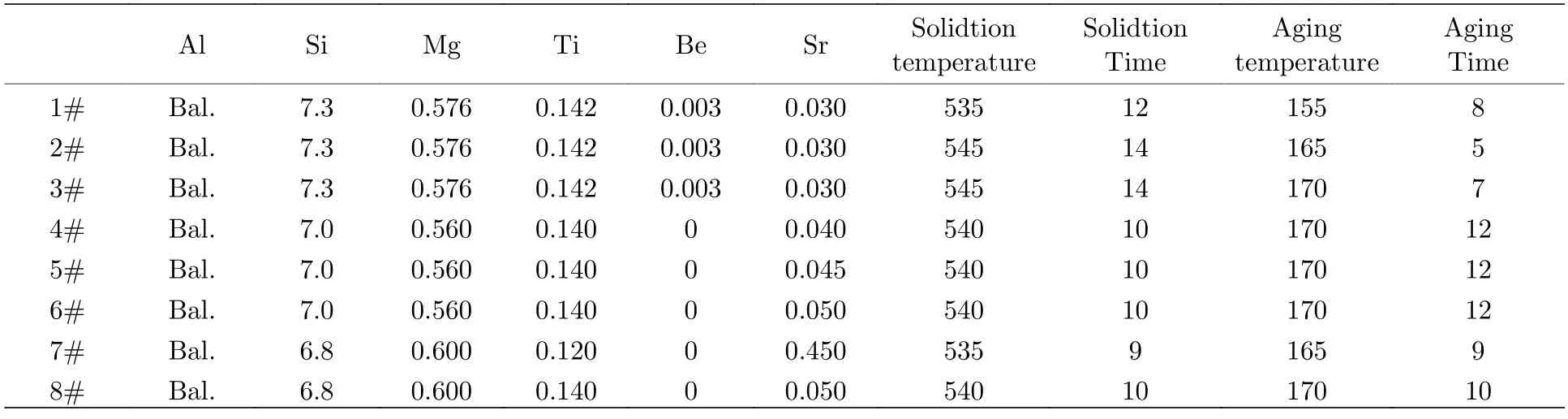
表1 新合金的成分和工艺Table 1.Composition and process of new alloys.
为了进一步显示基于模型所设计合金的综合性能,引入用来评估Al-Si-Mg 铸造合金拉伸性能的质量指数QDJR=UTS+150log(EL)[34](其中UTS为最终抗拉强度,EL 为伸长率),结果如表2 所示.
如表2 所示,经实验验证得到抗拉强度实验值与目标值相对误差控制在±5%之间,尤其通过第八组实验证实Al-6.8Si-0.6Mg-0.05Sr 的成分配比和540 ℃×10 h+170 ℃×10 h 工艺方案综合拉伸性能表现优异,QDJR质量指数达到517.3 (抗拉强度为349.6 MPa,伸长率为13.1%).
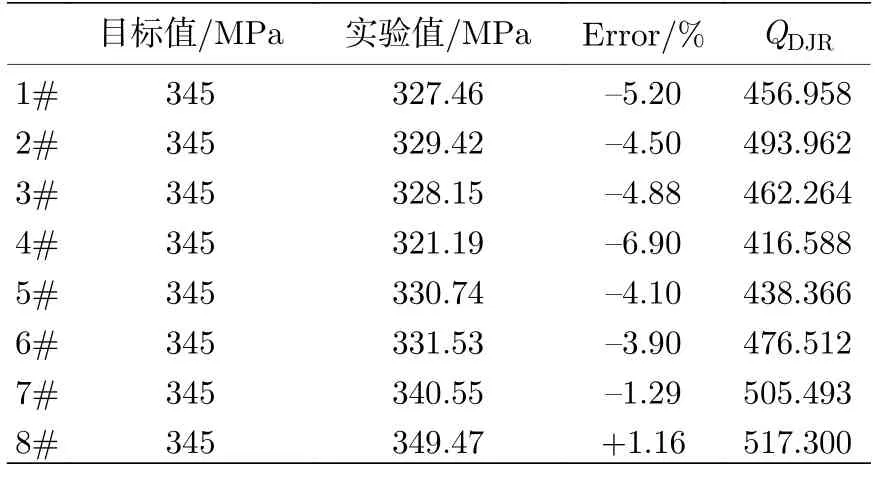
表2 实验结果及误差对比Table 2.Experimental results and error comparison..
5 讨论
5.1 多角度自变量对合金性能的影响
本研究中,为了表现模型在实际应用过程中的多样性和普适性,选取了多个不同尺度的特征变量如变质剂含量、变质温度、浇注工艺、热处理工艺等来研究其对抗拉强度的影响,结果如图7 和图8所示.图7(a)—(d)的误差带图分别对应变质剂含量[35]、变质温度[36]、模具温度[37]和浇注温度[37]的变化对合金性能的影响.图8(a),(b)是基于控制变量法分别从固溶工艺和时效工艺的角度评估模型预测合金性能的准确性[38].从图7 可以看到,随着特征自变量的变化,预测值相对于实验值始终保持在±5%的误差带内,由此说明模型可以针对不同自变量的变化做出准确的结果预测.在图8 中,模型不仅预测出在误差范围内的预测值,而且预测值整体呈现出来的变化趋势与实验值相同,这也证明通过模型可以在不进行试错实验的前提下就可以获得合金的最佳成分和工艺.
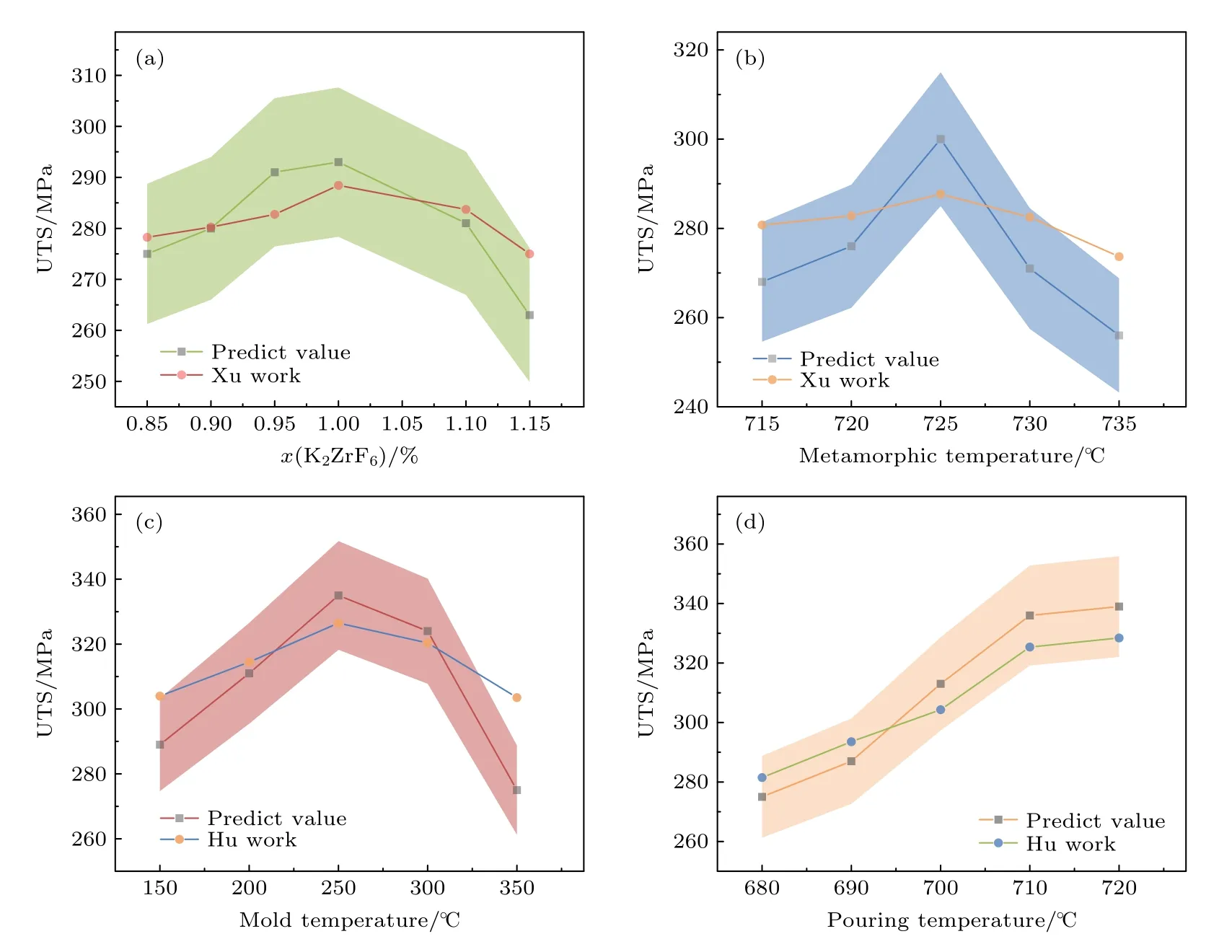
图7 性能预测结果 (a)变质剂K2ZrF6 的含量对合金性能影响;(b)变质温度对合金性能的影响;(c)模具温度对合金性能的影响;(d)浇注温度对合金性能的影响Fig.7.Performance prediction results: (a) The effect of the content of modifier K2ZrF6 on the properties of the alloy;(b) the effect of the modification temperature on the properties of the alloy;(c) the effect of the mold temperature on the properties of the alloy;(d) the effect of the pouring temperature on the properties of the alloy.
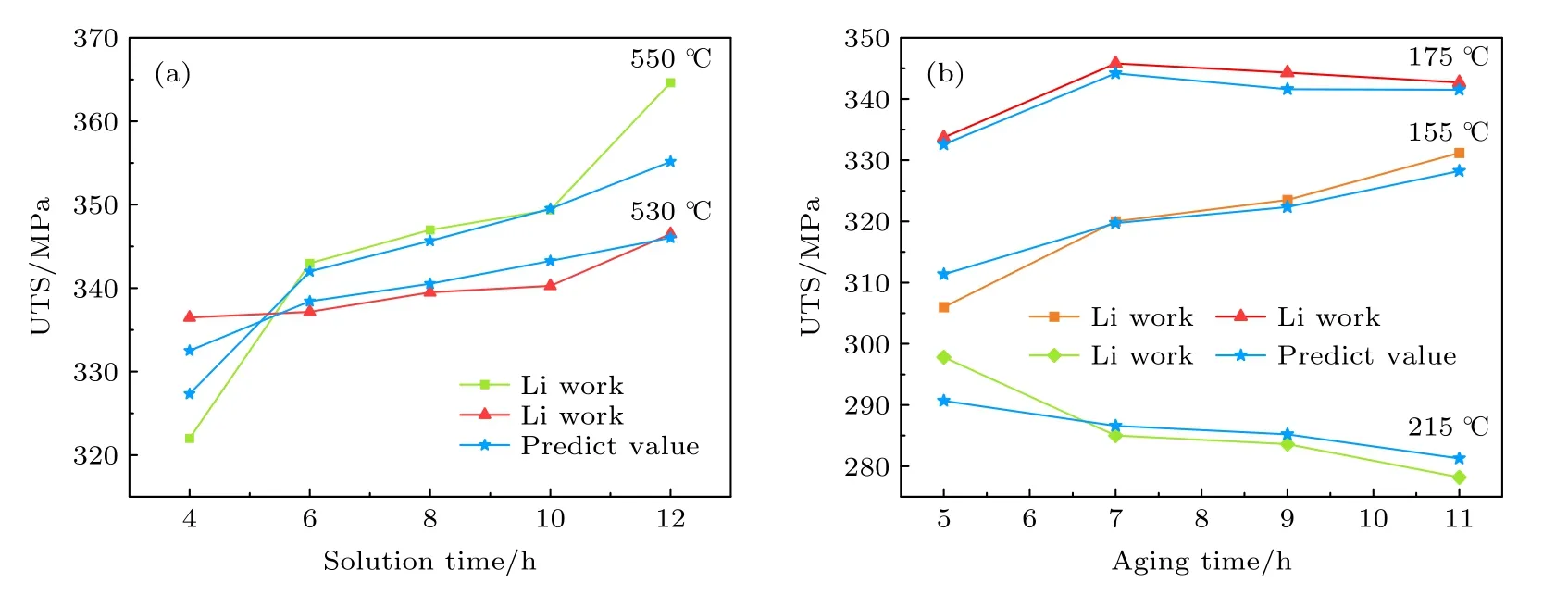
图8 基于控制变量法的合金性能预测结果 (a)固溶工艺对合金性能的影响;(b)时效工艺对合金性能的影响Fig.8.Prediction Results of alloy properties based on controlled variable method: (a) Effect of solution process on alloy properties;(b) effect of aging process on alloy properties.
和同类研究建立单一的成分-性能或热处理工艺-性能等的研究相比,本研究考虑了更多潜在的可以影响合金性能的因素,这不仅使得模型的预测结果更加准确,同时基于模型得到新合金的性能也更优于同类合金.如图9 所示,基于本模型得到Al-6.8Si-0.6Mg-0.05Sr 的成分配比和540 ℃×10 h+170 ℃×10 h 工艺方案综合拉伸性能与同类合金相比处于较高的水平,其QDJR质量指数达到517.3,高于同样使用Sr 变质(Al-7.069Si-0.676Mg-0.02Sr)的合金[22],以及使用稀土进行变质的同类合金[3−5].

图9 合金性能定量比较Fig.9.Quantitative comparison of alloy properties.
5.2 数字模拟实验的误差分析
本研究主要使用链式方程多重插补的方法对合金成分和工艺进行回归预测,并使用概率分布图对插补对象的准确性进行评估,如图10 所示.在原始数据旁边区分显示插补值的分布来判断预测结果与原始数据之间的分布差异,红线代表原始数据的分布,黑线则是每个数据集的插补(估算)值.在图中可以看到,通过对主要特征参数,如镁硅含量、变质剂含量、热处理工艺等的估算值的概率密度进行计算,将其所拟合出的曲线与原始数据的密度分布曲线比较,得出估算值的概率分布与原始数据整体分布规律基本一致,说明通过链式方程插补设计的合金的成分和工艺与原始数据在数据集中满足相同的概率分布.
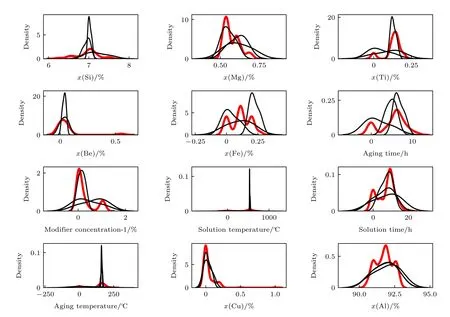
图10 预测概率分布图Fig.10.Prediction probability distribution map.
虽然模型预测结果符合原始数据的分布规律,但是最终预测的精度差异仍比较明显,例如在图7中仍然存在个别噪声点,曲线的增长趋势与实验值只是在误差带内保持同步.从模型角度分析发现目前研究热处理工艺对性能的影响的工作量远远超过熔炼工艺(见补充材料),这也导致数据集中以熔炼工艺为自变量的数据远远少于以热处理工艺为研究对象的数据,最终形成: 单一特征数据量的差异→模型对不同自变量泛化能力的差异→模型对不同自变量预测结果的差异;同时,对模型特征重要性进行量化时发现输入特征的重要性分数差别较大,如图11 所示,合金的热处理工艺在模型的重要性分数中所占比例最高,这也证明了热处理工艺特征在模型中发挥着与具体实验通过热处理提高合金性能相同的作用;对于合金成分的重要性分数来说,造成其差异的主要原因是基体元素Al,Si,Mg 外的其余元素是作为变质剂、细化剂进行添加的,其在整个数据集中的有效数据量远远低于基体元素,所以其重要性分数较低,最终导致模型对不同自变量预测结果的差异.
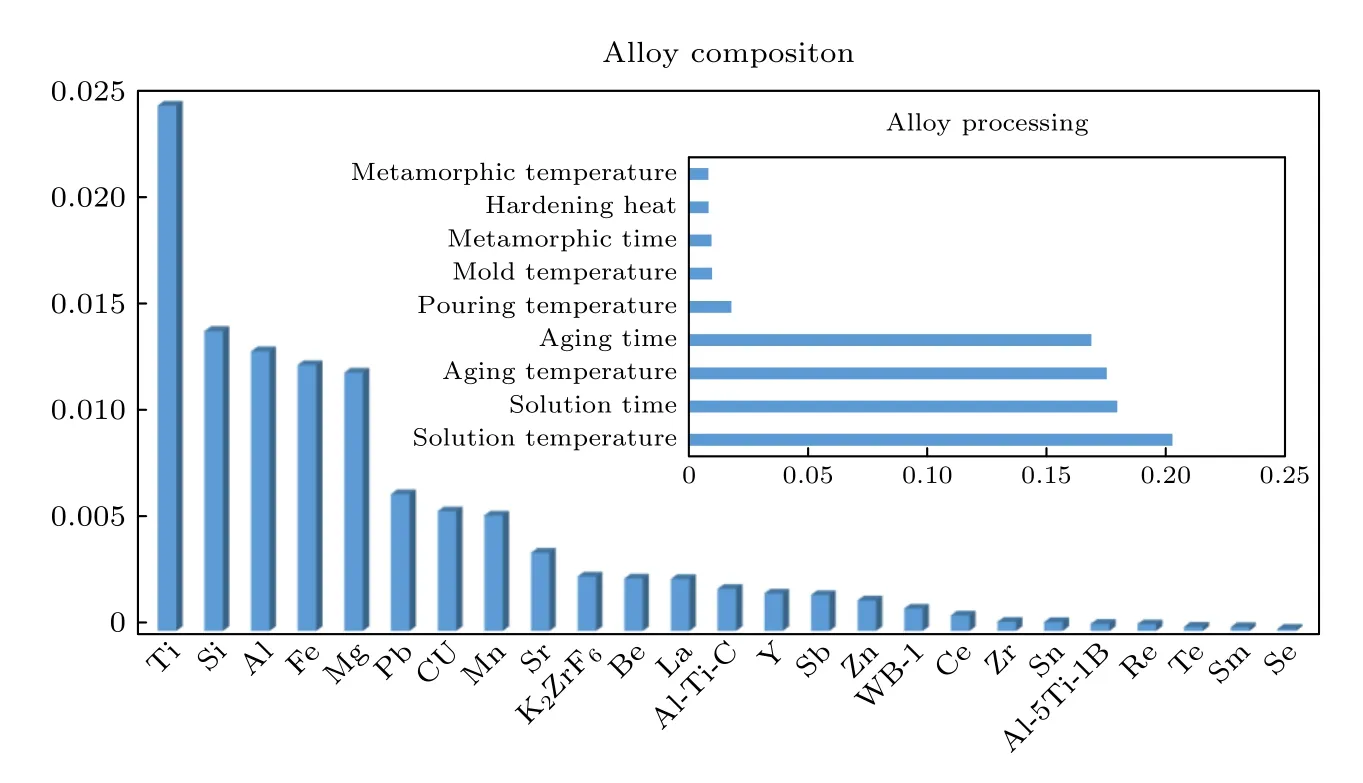
图11 特征重要性分数Fig.11.Feature importance.
因此可以确定,在一个模型中,当一部分小众化的研究特征出现在数据集中并作为研究对象时,其特征自身属性的差异以及其自身数据量的差异,都是造成模型预测效果差异的主要原因.
6 结论
基于机器学习搭建了多模态输入的Al-Si-Mg系合金性能预测-成分-工艺设计完整闭环模型.综合考虑实验过程中能够影响合金性能的因素,将同一体系不同牌号合金的成分、熔炼及热处理工艺等实验因素作为特征,通过随机森林寻找特征与性能之间的非线性规律,多角度,多变量的实现合金性能的预测;使用链式方程多重插补方法对目标数据进行回归预测,最终实现新合金成分和工艺的设计.结果表明: 模型中随机森林算法的决定系数可以达到0.989,使用链式方程多重插补算法得到的Al-6.8Si-0.6Mg-0.05Sr 的成分配比和540 ℃×10 h+170 ℃×10 h 工艺方案后经实验证实其综合拉伸性能表现优异,质量指数QDJR达到517.3 (抗拉强度为349.6 MPa,伸长率为13.1%),其他使用本模型改变多个自变量进行性能预测或指导设计的合金的抗拉强度误差均保持在±5%之内.这证实本文所建立的多模态数据库和机器学习模型可以很好地指导实验,缩短实验周期,降低实验成本,提高整体实验效率从而设计出更高性能的合金.

