叠层/转角二维原子晶体结构与极化激元的近场光学表征*
徐琨淇 胡成 沈沛约 马赛群 周先亮 梁齐 史志文
(上海交通大学物理与天文学院,人工结构及量子调控教育部重点实验室,上海 200240)
极化激元是一种光与物质发生强相互作用形成的准粒子,可以极大地压缩光波长,提供一种突破衍射极限的光调制方式,为纳米光子学、非线性光学、量子光学等相关学科的发展提供了重要支持.范德瓦耳斯二维原子晶体是研究极化激元的理想平台,通过叠层、转角可以为极化激元的调控提供额外的自由度,从而展示出新颖的光学结构和极化激元特性.本文以近场光学为主要研究方法,对近几年出现的叠层及转角二维原子晶体的各种光学结构及极化激元进行综述.综述内容包括叠层石墨烯的畴结构、转角二维原子晶体的莫尔超晶格结构、转角二维拓扑极化激元、转角石墨烯手性等离激元等.最后,对叠层/转角二维原子晶体及其极化激元的未来发展进行展望.
1 引言
极化激元是光与物质中携带电偶极或磁偶极的元激发之间发生强耦合形成的准粒子[1].极化激元可以大幅度压缩光波长,是一种有效突破衍射极限的光调制方式,为纳米光子学等前沿学科的发展提供了重要的支持,在未来信息传输与存储、光学传感检测等领域具有广泛的应用前景.
范德瓦耳斯二维原子晶体是研究极化激元的理想平台,一方面因为材料尺寸减小带来了新颖的光学性质,另一方面因为二维原子晶体能非常容易地通过层数、化学掺杂、外场等条件调控其能带结构、载流子浓度、介电环境等光学依赖的因素[2].不仅如此,通过堆叠、组装可以进一步丰富二维原子晶体结构,双层或多层二维原子晶体通过转角提供了一个额外的自由度,使范德瓦耳斯层间发生轻微晶格失配,引入层间杂化或耦合[3,4].因此,叠层及转角操作允许两个二维原子晶体重新组合并展示出单层材料所不具备的光学结构,并表现出新的极化激元性质.比如,叠层石墨烯中出现的畴结构、转角二维原子晶体中出现的莫尔超晶格网络、转角二维材料中出现的拓扑极化激元等.
根据二维原子晶体中偶极子类型的不同,极化激元主要包含以下几种类型: 自由电子体系中电子振荡为主导的表面等离极化激元[5],极性晶体中晶格振动为主导的声子极化激元[6],半导体中电子-空穴对激发过程中的激子极化激元[7,8]等.实验上用于研究极化激元的技术手段主要包括电子能量损失谱[9]、远场光学成像及光谱[10]、扫描近场光学显微技术(scanning near-field optical microscopy,SNOM)等.其中,SNOM 技术在研究极化激元方面具有其独特优势.首先,SNOM 是一种实空间成像技术,可以直接对极化激元波进行成像,并具有优秀的分辨率和解析力[11].由于倏逝场的局域性,SNOM 空间分辨率远超远场光学衍射极限达到纳米尺度[12,13].其次,借助于原子力显微镜纳米尺度的针尖,倏逝光场具有很宽的动量范围,可以激发不同动量能量的极化激元,实现激发检测同步进行.此外,SNOM 可在大气环境中工作、操作简单且对被测样品无损.因此,SNOM 技术已广泛用于低维材料极化激元的探索研究中.
本文拟对叠层及转角二维原子晶体所形成的各种光学结构及其极化激元进行综述,重点关注基于散射型扫描近场显微技术的极化激元性质研究.内容主要涵盖如下几个方面: 首先是对散射型扫描近场光学显微镜的结构和工作原理进行简要介绍;然后介绍几种常用的叠层及转角样品制备方法;接下来详细介绍不同转角及叠层二维原子晶体的结构特性和对应的等离激元性质,包括双层和三层石墨烯构成的堆叠畴和畴壁结构以及借助探针技术对其光学畴壁的纳米尺度操纵、几种转角二维原子晶体的莫尔超晶格结构、转角双层二维原子晶体的拓扑极化激元、转角双层石墨烯的手性等离激元;最后展望叠层及转角二维原子晶体的潜在应用及未来可能的发展方向.
2 扫描近场光学显微技术介绍
扫描近场光学显微技术是研究极化激元的主要方法之一,其装置以原子力显微镜(AFM)为基础,硬件系统主要由激光光源、扫描探针显微镜和光信号收集单元构成.早期的扫描近场光学显微镜采用光纤探针作为红外光激励源,后来被更高分辨率和信噪比的针尖散射型设计所取代[14,15].散射型扫描近场光学显微镜(scattering-type SNOM 或s-SNOM)的结构及工作原理如图1 所示,红外光汇聚到针尖-样品微区,散射的部分近场信号沿原路返回,经分束片反射,最终到达光探测器.

图1 散射型扫描近场光学显微镜示意图Fig.1.Schematic diagram of a scattering-type scanning near-field optical microscope (s-SNOM).
需要指出的是,由于散射式扫描近场光学显微镜的光路是开放的,探测器收集到的光不仅包含针尖散射出来的样品近场光信号,还含有探针悬臂及样品散射的远场背景光.为了得到纯净的近场光信号,通常采用针尖轻敲(tapping)模式,并利用锁相放大器解调将近场光与远场光分离.具体地,让AFM 探针以其谐振频率w0振动,振幅约50—100 nm.考虑到近场光主要分布在针尖尖端几纳米的空间范围内,因此每个振动周期仅在针尖和样品接触的一瞬间会散射出近场信号,所以近场信号的波形是快速变化的周期性脉冲序列,其傅里叶变换频谱中包含较多高阶分量(见图2).而来自准静态样品的远场散射背景光则近似为一个不随时间变化的常数;来自简谐振动针尖散射的远场背景光主要表现为简谐函数波形,其傅里叶变换频谱主要成分在针尖振动的基频w0上(见图2).因此,提取散射光中高阶频率(2w0,3w0或4w0)成分,即可有效地抑制远场背景光,得到较纯净的具有高空间分辨的近场光信号.
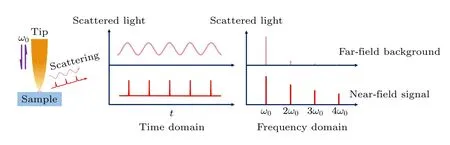
图2 近场光信号与远场背景光信号的波形及其频谱示意图Fig.2.Schematic diagram of the waveforms and Fourier components of near-field optical signal and far-field background noise.
运用s-SNOM 探测材料极化激元的工作原理如下.将激光汇聚在纳米尺度的金属针尖上,在针尖场增强效应作用下产生场强数百倍的局域光场.该局域光场由于空间受限而包含一个宽动量范围,有助于实现极化激元与自由传播光之间的动量匹配,从而有效地激发被测试样品中的极化激元.针尖局域光场激发的极化激元将沿着样品传播,并在边界处发生反射.反射的极化激元波与针尖尖端处的局域光场发生干涉,干涉的局域光场会改变针尖尖端处散射的光信号强度.该散射信号可被置于远场位置的光探测器检测到[2,16],再结合AFM 的面扫描功能就可实现样品中极化激元干涉图案的实空间成像.基于所测干涉图案可计算出极化激元的波长和品质因子等信息,进而获得极化激元的色散关系.
3 叠层及转角二维原子晶体的制备和调控
叠层/转角二维原子晶体可以通过多种方案制备,包括干法和湿法转移技术、生长合成技术、折叠技术及转角二维原子晶体的原位调控技术.不同的制备方案各有利弊,且各自具有不同的适用范围,接下来将依次简要介绍几种实验室常用的制备技术.
3.1 转移技术
转移技术主要分为干法转移以及湿法转移,该技术可以在转移的过程中实现叠层操作和调整转角,是实验室制备叠层及转角二维原子晶体最为常用的技术方案之一.
干法转移主要是以高分子有机物(如聚碳酸亚丙酯PPC、聚碳酸酯PC、聚二甲基硅氧烷PDMS等)作为转移媒介,利用不同温度下与高分子有机物的黏度变化来实现转移[17].由于材料只有其中一侧与有机物接触,在制备完成后这层有机物残留最终可以被等离子体退火过程处理,这使得所制备的叠层二维材料界面较为干净,非常有利于后续研究,其流程原理如图3(a)—(h)所示.基于干法转移发展而来的“撕裂堆叠”(shear and stacking)技术可实现二维材料更为精准的转移(最高0.1°的转角控制),界面也较为洁净[17].干法转移是目前制备高质量叠层/转角二维原子晶体优先考虑的方法.

图3 干法转移制备转角石墨烯的流程原理图 (a),(e)二维材料拾取示意图,红色框表示半球形基板的放大视图;(b)—(d)和(f)—(h)连续堆叠步骤的示意图和相应光学显微照片[17]Fig.3.Schematic diagram of the dry transfer to fabricate twisted bilayer graphene[17]: (a),(e) Schematic diagram of layer pick-up,the red box represents a zoom-in view of the hemispherical handle substrate;(b)–(d) and (f)–(h) the schematic diagrams and optical micrographs of successive stacking steps[17].
湿法转移的主要操作方法是通过刻蚀材料基底使其悬浮在液体表面,然后使用待转移的基底将材料从液体中取出.在制备转角二维材料时,可在材料生长合成前先将衬底的某个区域进行疏水处理,在生长出大面积二维材料后,将材料浸入液体中.在液体的作用下,疏水区域的二维材料依然可以附着在衬底上,而在亲水侧会悬浮在液体中,再将衬底缓慢从亲水侧拉出,从而完成材料的制备[18].这种方法通常适用于大面积材料的转移,其缺点是需要与刻蚀液体接触,这就不可避免地使残留的有机污染物被封装在材料与衬底之间.
3.2 生长合成技术
转移技术目前已被广泛使用,然而该技术对污染物、尺寸和晶格方向的精确控制依然存在一定的不足,从而限制了许多实际应用.为了弥补这些不足,生长合成技术提供了一种自下而上的生长策略,可以带来理想的效果.生长合成技术包括物理气相沉积(PVD)、化学气相淀积(CVD)、原子层沉积(ALD)、分子束外延生长(MBE)等.最近,Liu等[19]使用CVD 方法制备出任意转角的大面积双层石墨烯.到目前为止,生长合成技术被认为是低成本、大面积、高质量的制备叠层/转角二维原子晶体极有前景的技术方案.
3.3 折叠技术
折叠技术是一种获得同质叠层二维原子晶体结构的一种快速且相对容易的方法.二维材料通过相对较弱的范德瓦耳斯力相互作用结合在衬底上,因此二维材料与衬底表面之间的相互作用可以通过其他更强的力来打破.早期的研究发现,SiO2衬底上的薄层石墨烯材料可以在被水冲洗后发生折叠[20],但这种方案并不可控.为了克服这个问题,研究人员发展出了通过高分子有机薄膜吸附二维材料折叠的方案,这使得折叠过程变得更加可控,同时制备出的样品层间也非常干净(见图4)[21].最近,折叠技术又得到了进一步的发展,即使用扫描隧道显微镜探针吸附二维材料的一角,然后进行堆叠,该技术具有原子级的堆叠精度、不引入杂质以及可重复操作的优点[22].
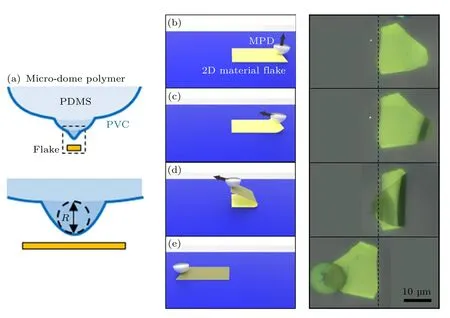
图4 基于微型半球状聚合物凝胶的二维材料薄片折叠技术原理图[21] (a) PDMS 微型半球状聚合物凝胶结构示意图;(b)—(e)二维材料薄片折叠连续操作示意图和相应光学显微照片Fig.4.Schematic diagram of two-dimensional material sheet folding technology based on microdome polymer gel[21]: (a) Schematic diagram of the structure of PDMS microdome polymer gel;(b)–(e) the schematic illustrations of folding two-dimensional material sheet and corresponding optical micrographs of successive steps.
3.4 转角二维原子晶体的原位调控技术
使用以上方案制备出的材料与器件,一旦制备完成,通常很难再对其转角进行调控,为此,研究人员发展出了多种二维原子晶体转角原位调控的技术.其中,采用高分子有机薄膜吸附叠层二维材料并操纵其转角是实验室较为常用的技术.该技术在叠层二维材料上使用电子束光刻(EBL)工艺制作聚甲基丙烯酸甲酯(PMMA)层,并用PDMS 微型半球状凝胶作为操纵器,接触并操纵PMMA 层旋转,进而使叠层二维材料实现转角操作(如图5(a)—(c))[23].最近,Hu 等[24]发展出了一种使用AFM 探针操纵双层二维原子晶体转角的原位调控技术(如图5(d),(e)).利用二维原子晶体在非公度状态下的超滑效应,可以使得其层间轻易发生相对滑动[25,26].该技术的独特之处在于,在上下两层石墨烯之间,插入了原子级厚的hBN 空心齿轮结构,在齿轮的中间空心区域,上下两层石墨烯接触,形成转角区域.使用AFM 探针推动hBN 齿轮,能够精确地控制石墨烯重叠区域的扭转角度.这一技术为研究双层石墨烯的转角效应提供了机会,可以在很大程度上推进转角光电子学的研究.
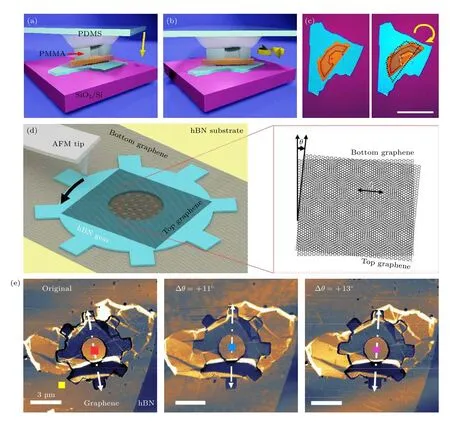
图5 转角二维原子晶体的原位调控技术 (a)—(c)使用PDMS 微型半球状聚合物凝胶操纵叠层二维材料实现转角操作,(a),(b)为方法示意图,(c)展示了样品转角前后的光学成像,标尺为40 µm[23];(d),(e)使用AFM 探针操纵双层二维原子晶体转角的原位调控技术,(d)为方法示意图,(e)为样品转角前后的AFM 成像[24]Fig.5.In situ manipulation of twisted two-dimensional atomic crystals.(a)–(c) Applying PDMS microdome polymer gel to manipulate the stacked two-dimensional materials to twist.(a),(b) Schematic diagrams of the method.(c) The optical images of the sample before and after twisting.Scale bar is 40 µm[23].(d),(e) In situ manipulation of twisted bilayer two-dimensional atomic crystals using AFM probes.(d) A schematic diagram of the method.(e) The AFM images before and after twisting[24].
4 二维原子晶体堆叠次序及堆叠畴壁的近场光学表征
叠层二维原子晶体会因为不同的堆叠形式产生线缺陷或原子重构等现象,这可能会出现由于层间效应和面内应变导致的有趣特性.石墨烯是一种备受关注的二维材料,由于其半金属特性,以及近乎完美的二维自由电子气体系,为等离激元学及相关光电器件的发展提供了良好的平台.目前,单层石墨烯边界[2,16,27]、晶界[5]、台阶[28]的极化激元性质已有大量的研究,可以预见,叠层石墨烯会提供更丰富的光电性质.
4.1 双层石墨烯中的堆叠畴壁
双层石墨烯中存在两个等价的最低能量堆叠次序 AB 和 BA[29,30].AB 和 BA 堆叠的双层石墨烯畴区之间的过渡区域会形成类似孤子的一维畴壁[31],该畴壁是一种独特的线缺陷,拥有受拓扑保护的谷量子霍尔绝缘体的手性边缘态[32,33],可形成一维谷极化导电通道,有助于增强畴壁对于红外光的响应[34].
Ju 等[35]使用s-SNOM 对双层石墨烯层堆叠畴壁进行原位成像(如图6(a),(b)),AFM 形貌图(如图6(a))中无法显示表面畴壁的缺陷,而在对应的近场红外成像中(如图6(b))显示出了光电导率增强的一维亮线,即一维畴壁.不仅如此,叠层石墨烯的畴壁处可以观察到较强的表面等离激元反射[36].双层石墨烯中可以存在不同类型的孤子畴壁,具体取决于孤子畴壁相对于过渡区位错矢量的方向: 平行于位错矢量的是剪切应变,而垂直于位错矢量的是拉伸或压缩应变(如图6(c),(d)).机械剥离制备的双层石墨烯中天然存在多种畴壁结构,并且等离激元的性质表现出对畴壁孤子类型的显著差异性.如图6(d)所示,剪切型畴壁展示出单亮线特征,拉伸型畴壁展示出双亮线特征.剪切应变畴壁与正应变畴壁相比,其反射相位相差π/2;由于剪切孤子畴壁比正应变孤子畴壁宽度更薄,因此反射率更低[36].此外,随着栅极电压从60 V 到–80 V 的调控,拉伸畴壁孤子处的双亮线特征增强且线分离增加;对于剪切畴壁孤子,单亮线特征变强,并逐渐变成三亮线,表现出畴壁处等离激元对栅极电压调控的强烈依赖性[34,36](如图5(e),(f)).

图6 堆叠双层石墨烯中的孤子畴壁 (a)双层石墨烯样品在 SiO2/Si 衬底上的 AFM 形貌图,右下角的小三角形区域对应于单层石墨烯;(b)与图(a)对应的近场光学成像[35];(c)剪切(上图)和拉伸(下图)畴壁孤子的示意图,虚线勾勒出 AB 堆叠平滑过渡到 BA 堆叠的畴壁区域,箭头表示位错方向;(d)双层石墨烯的近场光学成像,展示了弯曲的 L 形畴壁;(e)不同栅极电压下双层石墨烯中剪切孤子和拉伸孤子的近场光学成像,标尺为 300 nm;(f)对应图(e)中白色虚线处的扫描线,展示了在拉伸孤子处栅极依赖的等离激元干涉行为,用虚线表示的两个峰对应于两条亮线,它们的分离随着载流子密度的增大而增加[36]Fig.6.Soliton domain walls in stacked bilayer graphene: (a) AFM topography of the bilayer graphene sample on SiO2/Si substrate,the small triangular area in the lower right corner corresponds to the monolayer graphene;(b) near-field optical image corresponding to Fig.(a)[35];(c) schematic diagrams of shear (top) and tensile (bottom) domain wall solitons,the dashed line outlines the domain wall region where the AB stacking domain smoothly transitions to the BA stacking domain,arrows indicate dislocation directions;(d) near-field optical imaging of bilayer graphene,showing L-shaped domain walls;(e) near-field optical images of shear and tensile solitons in bilayer graphene at different gate voltages,scale bar is 300 nm;(f) corresponds to the scan line at the white dashed line in Fig.(e),showing gate-dependent plasmon interference behavior at the tensile soliton,the two peaks represented by dashed lines correspond to two bright lines,and their separation increases with increasing carrier density[36].
4.2 三层石墨烯堆叠畴
在三层及以上的多层石墨烯中,每层石墨烯都会提供额外的自由度,且不同堆叠顺序意味着构建新的结构对称性,会强烈影响其光电子特性,包括能带结构[37−40],自旋轨道耦合[41],层间屏蔽[42]等.对于三层石墨烯,存在两种稳定的晶体结构: 顶层直接位于底层之上(表示为 Bernal 或 ABA 堆叠),或者位于底层六边形中心的上方(表示为菱面体或 ABC 堆叠)[43,44].最近的研究表明[37,45−47],由于不同的层间电子相互作用和不同的晶体对称性,这两种类型的三层石墨烯具有不同的物理特性:ABA 堆叠的三层石墨烯是一种半金属,而 ABC堆叠的三层石墨烯在栅极电压调控下可由半金属转变为半导体.
比较特别的是,在三层石墨烯中,可以同时形成ABA 和ABC 堆叠的两种畴区,从而产生面内ABA/ABC 异质结构,两种结构过渡的畴壁区域,由局部应变孤子构成.与双层石墨烯类似,三层石墨烯两种结构对应的畴区以及之间的畴壁同样无法直接通过传统的AFM 形貌像进行分辨(如图7(a)).不同的是,由于三层石墨烯两种结构光电性质的根本差别,光学方法包括近场光学、拉曼光谱等技术均可以实现畴区分辨[44,48].
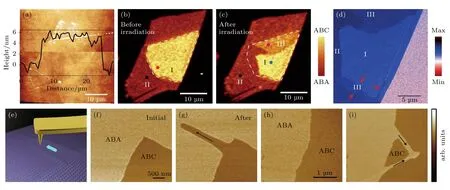
图7 三层石墨烯的多种畴区 (a)衬底上三层石墨烯的 AFM 形貌像和高度剖面图;(b),(c)三层石墨烯样品激光照射处理前、后的拉曼成像;(d)激光照射后三层石墨烯的近场光学成像,具有不同堆叠顺序的畴区在近场光学像中显示出不同的衬度,标记的区域 I,II 和 III 分别对应于 ABC 堆叠、ABA 堆叠和混合 ABC+ABA 堆叠畴区,红色箭头标记了在拉曼图中未显示出的额外混合 ABC+ABA 堆叠区域[48];(e)使用AFM 接触模式对三层石墨烯畴壁进行操纵的示意图,蓝色箭头表示尖端的移动方向;(f)—(i)三层石墨烯的两个区域在沿着黑色箭头对畴壁进行单线扫描前后,畴壁形态变化的近场光学成像[49]Fig.7.Various domains of trilayer graphene.(a) AFM image and height profile of trilayer graphene on the substrate.(b),(c) Raman imaging of three-layer graphene samples before and after laser irradiation.(d) Near-field optical image of trilayer graphene after laser irradiation.Graphene domains with different stacking orders show different contrasts in near-field optical images.Marked regions I,II,and III correspond to ABC stacking,ABA stacking,and mixed ABC+ABA stacking domains,respectively.Red arrows highlight additional mixed ABC+ABA stacking domains not shown in the Raman map.[48] (e) Schematic diagram of the manipulation of trilayer graphene domain walls using AFM contact mode.The blue arrow indicates the direction of movement of the tip.(f)–(i) Near-field optical images of domain walls with the reconstructed configuration before and after single-line scanning along the black arrows in trilayer graphene[49].
Jiang 等[49]使用s-SNOM 究了双层和三层石墨烯的孤子畴壁.在近场红外成像中,双层石墨烯与三层石墨烯的畴壁在近场响应上具有明显的区别.在双层石墨烯中,其畴壁的近场成像为一条亮线,其分隔了双层石墨烯中AB 和BA 不同畴堆叠的区域,而AB 和 BA 堆叠畴之间的红外成像衬度并无差别.与之对比,在三层石墨烯中,ABA 和ABC 堆叠畴区具有不同的红外响应衬度.
通过体材料石墨直接机械剥离获得的三层石墨烯是以ABA 堆叠顺序为主,也存在着少量ABC堆叠构型,这是因为ABA 堆叠构型比ABC 堆叠在热力学上更具稳定性[48].对于存在ABA/ABC孤子畴壁的样品,激光可以诱导局域加热效应,从而驱动 ABC 到 ABA 的相变[48],精确控制激光束的移动,能够重塑畴并操纵三层石墨烯中畴壁的位置和方向(如图7(b)—(d)).不仅如此,Jiang 等[49]结合AFM 探针技术和s-SNOM 成像研究发现,畴壁可以通过AFM 尖端施加的机械应力来移动(如图7(e)—(i)).这意味着,可以用高精度的探针通过机械作用力的方式灵活地操纵并创建定制化的畴结构.
5 转角双层二维原子晶体莫尔超晶格的近场光学表征
莫尔超晶格结构来自于在小转角堆叠的相邻原子层之间的晶格失准或失配,例如在转角的双层石墨烯[50,51]、hBN、过渡金属硫化物[52]等二维原子晶体中会产生周期性超晶格结构.由于应变的存在,两个叠层之间会发生重构,并以具有最低简并能的原子晶格顺序进行堆叠.在面内共存的两个畴的过渡区会产生应变孤子畴壁,这导致了二维原子晶体表面被畴壁划分为周期性的网格.不同对称性的二维原子晶体转角所获得的莫尔图案也有所不同,并且可以通过转角大小来调控.这种图案导致长程层间耦合,极大地改变了电子结构和材料特性.周期性的超晶格结构会影响其中极化激元的传播,使用s-SNOM 是较好的研究方法.目前,已报导的相关的研究中,涉及有转角石墨烯、hBN 等二维材料.
5.1 转角石墨烯
由于单层石墨烯的六重对称性,转角双层石墨烯中会产生三角形莫尔超晶格,表面被AB 和 BA区域所形成的畴壁分隔[50,51](如图8(a)所示),周期性的网格由于晶格重构形成孤子畴壁,且转角可以调制三角形网格的区域大小和周期[50].2016 年,Jiang 等[36]使用s-SNOM 观察到了双层石墨烯中三角形格子组成的孤子畴壁网络,所有畴壁都显示了单亮线的近场红外响应特征(如图8(b)所示).2018 年,Sunku 等[50]进一步对转角双层石墨烯莫尔超晶格中的等离激元行为进行研究.当s-SNOM激发光波频率接近 SiO2衬底的光学声子时,可观察到六重对称性的网格成像,揭示了转角导致的孤子畴壁局域光电导率的增强.研究人员还发现转角双层石墨烯中的等离激元可以被孤子阵列所散射[34,36],与晶界类似[5].
对于基于转角双层石墨烯的器件,经常有添加顶栅的工艺和表面保护的需要,一个可选择的方案是采用覆盖薄层hBN 来封装,而hBN 的介入会减少探针与石墨烯样品之间的近场光学响应强度.Luo 等[53]制备了hBN/转角双层石墨烯/hBN 叠层异质结构,并调谐红外光激励频率,研究发现1500—1620 cm–1的波数显著增强了hBN 中声子极化激元在畴壁处的反射,是可视化内部转角石墨烯的莫尔图案的最佳频率范围.在不同的红外光频率下,该叠层异质结构表现出不同的极化激元特性,其近场红外成像结果如图8(c)—(h)所示.
双层石墨烯莫尔周期性结构也可以用近场光电流表征方法来可视化.Hesp 等[54]和Sunku等[55]分别实现了莫尔超晶格内部的近场光电流成像,该光电响应来自于近场光诱导莫尔超晶格精细结构中产生的光热电效应,其实验结果如图8(i)—(k)所示.
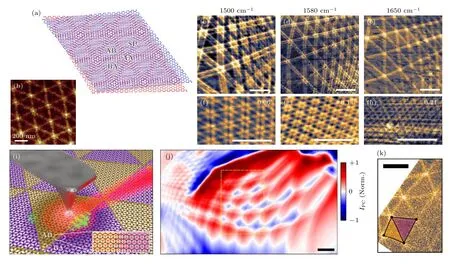
图8 转角双层石墨烯的莫尔超晶格网络 (a)转角双层石墨烯不同堆叠构型,分别用AB,BA,AA 和SP 标记;(b)转角双层石墨烯周期性三角形孤子畴壁的近场光学成像[36];(c)—(e)在不同激发频率下,hBN 封装的转角双层石墨烯莫尔图案的近场光学成像,转角为~0.05°;(f)—(h)在激励频率w=1560 cm–1 下,分别为0.06°,0.11°和0.21°的不同转角的近场光学成像,标尺为500 nm[53];(i)转角双层石墨烯近场光电流成像的实验设置示意图,叠层石墨烯中标记有AB 和BA 畴区;(j)转角双层石墨烯的光电流成像;(k)对应于图(j)中的黄色虚线矩形的近场光学相位图,标尺为500 nm[54]Fig.8.Twisted bilayer graphene superlattice network.(a) Schematic diagram of twisted bilayer graphene showing different stacking configurations.They are marked with AB,BA,AA and SP respectively.(b) Near-field optical images of the periodic triangular soliton domain-wall lattice of twisted bilayer graphene.[36] (c)–(e) Near-field optical images of the normalized amplitude showing moiré pattern in buried twisted bilayer graphene encapsulated with hBN at different excitation frequencies.The twist angle is~0.05°.(f)–(h) Near-field optical images showing different twist angles of 0.06°,0.11° and 0.21° at excitation frequency ω=1560 cm–1.Scale bars are 500 nm.[53] (i) Schematic diagram of the experimental setup for near-field photocurrent images of twisted bilayer graphene with AB and BA labels in stacked graphene layers.(j) Photocurrent map of twisted bilayer graphene.(k) Near-field optical phase image corresponding to the yellow dashed rectangle in Fig.(j).Scale bar is 500 nm[54].
此外,转角双层石墨烯不仅能形成周期性莫尔超晶格结构,而且转角依赖的层间电子耦合能显著影响其等离激元的性质[56−58].Hu 等[57]通过扫描近场光学显微镜对转角双层石墨烯中的等离激元行为进行了研究,其显微成像显示这些等离激元对转角有明显的依赖关系.在较小的转角下,其等离激元波长与单层石墨烯相当.在较大的转角下,等离激元波长显著增大,阻尼明显降低.为了理解这种行为,研究人员通过数值模拟发现,转角的双层石墨烯在狄拉克线性区,其莫尔超晶格势和层间耦合对狄拉克费米子有调制作用,使费米速度发生重整化,从而导致了等离激元波长对转角的依赖性.
5.2 转角六方氮化硼
不仅仅是转角的双层石墨烯,其他二维原子晶体如hBN 中的层间原子平面失配也会形成莫尔超晶格.Ni 等[59]使用s-SNOM 成功实现了hBN 晶体亚表面孤子超晶格的可视化.其超晶格形成于hBN 晶体表面下方约 15 nm,近场光学成像显示为六边形网络(如图9(a)).该hBN 畴区和畴壁对红外光频率有着不同的响应,反映了系统内部不同的弹性应变分布(如图9(b)).由于这种莫尔超晶格结构产生于较厚的薄片状晶体的亚表面界面处,其构型与原子级的薄层转角hBN 有较大差别.原子级的薄层转角hBN 与石墨烯类似,Bernal 堆叠构型的hBN 表面同样会被分割为AB 和BA 的周期性三角形网格畴区.为了研究其声子极化激元性质,Moore 等[60]在石墨衬底上,通过机械剥离的方法构建了原子级厚的转角hBN 样品.该研究团队分别使用压电响应显微术(piezoresponse force microscopy,PFM)[61,62]和s-SNOM 对其进行成像,两者均清晰的显示了AB 和BA 的三角形畴区(如图9(c)—(j)).近场光学成像(如图9(e)—(j))显示出AB、BA、畴壁鞍点(SP,三角形边)、三角形顶点AA 各区域不同的衬度,其衬度归因于转角hBN 面内畴结构各区域的声子极化激元的红外光频率依赖性,反映了其面内横光学支(波数为1360—1380 cm–1)声子共振系统的空间分布.图9(k)—(m)展示了hBN 不同堆叠区域的介电函数实部(图9(k))和虚部(图9(l))的频率依赖性,显示出各区域的横光学支声子频率偏移(具体数据见图9(m)).该团队通过实验和第一性原理计算进一步研究显示,面内应变不足以引起可分辨的横光学支声子频率的差异,这种差异主要来自于 hBN 与其公度的石墨衬底之间极化激元耦合的贡献.

图9 转角hBN 超晶格网络 (a)频率为1368 cm–1 处的转角hBN 畴结构的近场光学成像;(b)转角hBN 声子剩余极化带的近场光学信号的频率依赖关系图,纵坐标表示畴区和畴壁的信号比值,插图显示了对应的近场光学像[59];(c)转角hBN 在石墨/SiO2/Si衬底上的近场成像示意图,该图展示了可能的堆叠构型(AA,AB,BA);(d)转角hBN 的压电响应显微术(PFM)成像,插图显示了直流静电力显微术(DC-EFM)成像;(e)—(j)在3 个选定频率下拍摄的转角hBN 的近场光学振幅和相位的图像,对应图(d)中白色虚线矩形显示的区域,所有实验都是在横向光学(TO)声子调谐频率附近进行的;(k),(l)不同堆叠构型的介电函数对频率的依赖关系;(m)相关拟合参数,反映不同堆叠构型的频率偏移[60]Fig.9.Twisted hBN superlattice networks.(a) Near-field optical image of the twisted hBN domain structure at a frequency of 1368 cm–1.(b) Frequency-dependent plot of the near-field optical signal of the phonon restrahlen band of the twisted hBN.The yaxis represents the signal ratio of the domain region and the domain wall.The inset shows the corresponding near-field optical image.[59] (c) Schematic diagram of near-field optical imaging of twisted hBN on a graphite/SiO2/Si substrate.The possible stacking configurations are drawn above (AA,AB,BA).(d) Piezo-force microscopy (PFM) image of twisted hBN.The inset shows DC electrical force microscopy (DC-EFM) imaging.(e)–(j) Images of the near-field optical amplitude and phase for twisted hBN at three selected frequencies,corresponding to the area marked with white dashed rectangle in Fig.(d).All experiments are performed at the transverse optical (TO) phonon frequency.(k),(l) Frequency dependence of the dielectric functions of different stacking configurations.(m) The fitting parameters,which reflect the frequency shift of the different stacking configurations[60].
石墨烯与hBN 有相近的晶格参数使其叠层转角结构也可以产生莫尔超晶格[63,64],堆叠的石墨烯/hBN 异质结构在超晶格区域边界处获得了卫星亚狄拉克锥(satellite sub-Dirac cones),导致许多有趣的新行为[3,65−67].Ni 等[68]利用s-SNOM 研究了石墨烯/hBN 异质结构中的表面等离激元性质.该异质结样品的制备方法是在hBN 基底上使用无催化CVD 外延生长获得薄层石墨烯[69],在石墨烯/hBN 叠层样品中可同时产生纳米级莫尔超晶格畴区与普通(无超晶格效应)石墨烯畴区,且这两种畴区直接相邻.近场光学成像显示莫尔超晶格畴区比普通石墨烯畴区有更强的近场光学响应.为理解这种行为,该项研究通过第一性原理计算得到了石墨烯/氮化硼莫尔超晶格结构的能带结构,与经典的狄拉克锥能带相比,其能带具有精细的子带结构.这些劈裂的子带结构打开了额外的光吸收通道,从而增大材料的光电导率,最终导致莫尔超晶格畴区近场光学信号的增强.此外,该项研究还发现两种畴区的边界会发生与晶界类似的等离激元反射现象,畴壁两侧具有相近的波长,但莫尔超晶格畴区一侧等离激元表现出更高的阻尼.
6 转角二维原子晶体的拓扑极化激元
根据极化激元等能线(面)的几何形状,它们一般可以分为椭圆型和双曲型两类.当材料的介电张量分量[εxx,εyy,εzz]出现正负异号时,就能支持双曲型极化激元的传播.双曲极化表面具有开放的双曲色散、极大的光学态密度和特定的极化激元传播方向,这产生了诸多不寻常的现象,如负折射、自发辐射增强等.传统上双曲型材料主要通过人工构筑金属阵列图案组成的超材料来实现,而一些极端各向异性的天然二维原子晶体,其特定取向也能表现出负介电函数,从而支持双曲型极化激元的传播.这些天然二维原子晶体兼具光电可调谐的能力和原子级平整的表面,在优化纳米尺度加工并发展双曲超材料方面更具优势.目前,在范德瓦耳斯二维原子晶体中已报道支持双曲极化激元的包括α-MoO3[70,71]、α-V2O5[72](面内声子极化激元)、hBN[73,74](面外声子极化激元)、WTe2[75](面内等离激元)模式、WSe2[76](面外激子极化激元)、黑磷[77,78](理论预言面内等离激元和激子极化激元)等,进一步对双曲型二维原子晶体进行叠层转角操作,可获得其极化激元的新特性,如拓扑极化激元.
6.1 转角双层α-MoO3 的“光子魔角”
2018 年,Zheng 等[70]和Ma 等[71]分别 对α-MoO3范德瓦耳斯二维原子晶体的声子极化激元进行了近场光学研究,结果表明,对于薄层α-MoO3在其剩余极化带内,介电常数的实部沿 [100] 方向(x轴)为负,但沿 [001] (y轴)方向为正(晶体学取向定义如图10(a)所示),这种极端的各向异性使其面内声子极化激元具有双曲线响应[6,74,79].
然而,如何调控二维声子极化激元的拓扑转变是该研究方向更加关心的问题.2020 年,Hu 等[80]利用双层旋转的石墨烯纳米光栅阵列构成了双曲超表面.通过旋转角度的变化实现了可控的光学色散关系.在该体系中,当上下两层石墨烯纳米光栅阵列被旋转到特定角度时,会形成两个近乎平行的色散曲线,进而形成一个低损耗宽波段的传输渠道.
同年,Hu 等[81]又通过转角两层α-MoO3实现了对其声子极化激元色散的精确控制.使用s-SNOM进行实空间成像研究发现,这种声子极化激元的色散轮廓可以通过转角调控实现从双曲线(开放)到椭圆(闭合)的拓扑转变.这种转变可由一个拓扑量来标定,即每层的色散曲线在倒空间中的反交叉点(NACP)的数量.当NACP为 2 时,色散是双曲线的;当其为 4 时,色散是椭圆的.NACP变化的临界转角被称为“光子魔角(photonic magic twist angle)”.声子极化激元拓扑结构从封闭变为开放时,可产生低损耗的定向传输通道.在同一时期,Chen 等[82]和Zheng 等[83]两个团队对这一现象分别进行了独立研究,并给出了类似的结果,对应的实验结果如图10(b)—(q)所示.
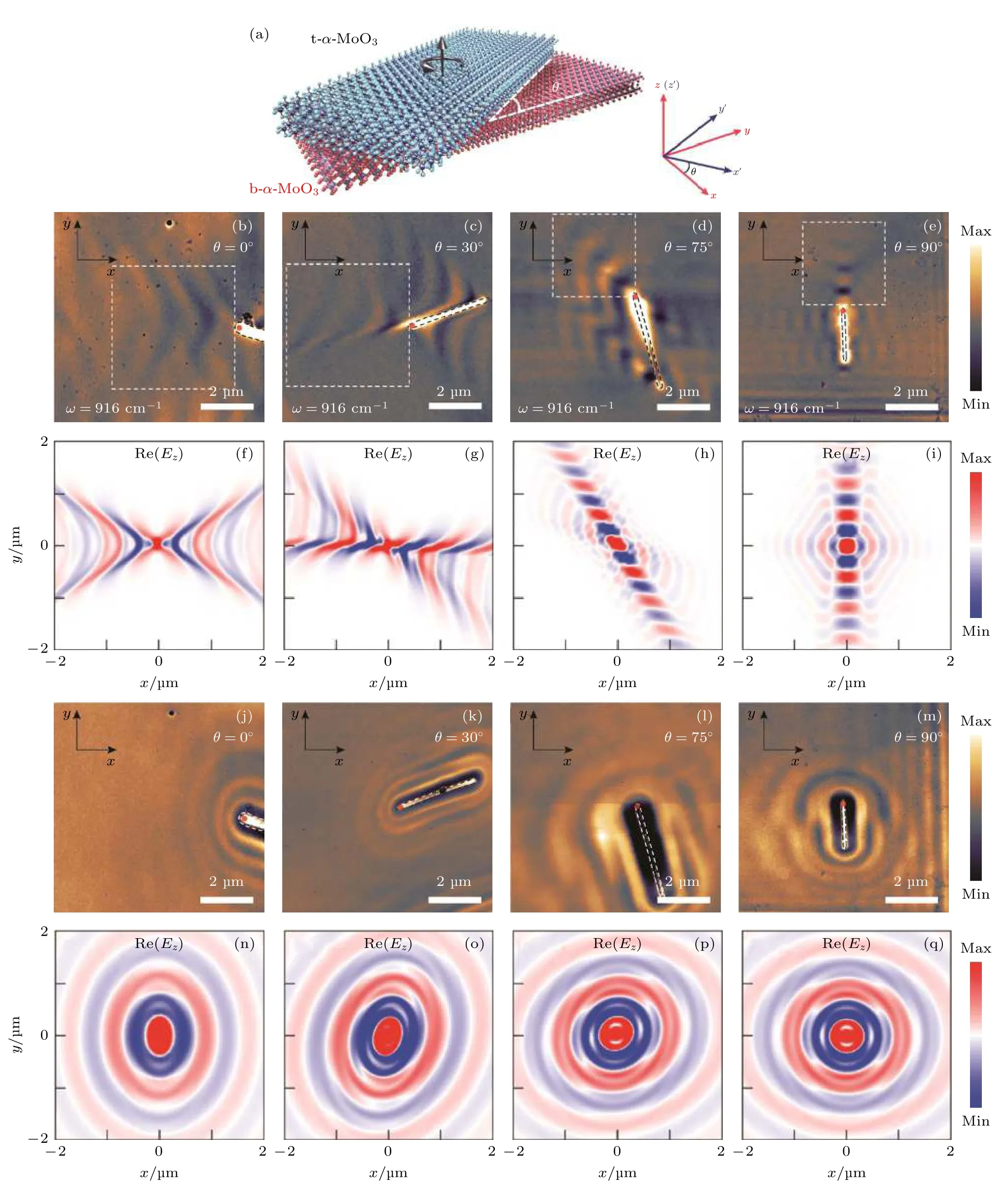
图10 转角双层α-MoO3 的声子极化激元的拓扑转变[83] (a)转角双层α-MoO3 示意图.底层α-MoO3 的 [100] 和 [001] 方向分别定义为x 和 y 轴,转角 Δθ 定义为顶层α-MoO3 相对于底层逆时针旋转角度;(b)—(e)和(j)—(m)显示了真实空间近场光学成像,反映了声子极化激元色散作为转角的函数的拓扑性质,频率为916 cm–1(图(b)—(e)和986 cm–1(图(j)—(m));(f)—(i)和(n)—(q)对应计算的电场分布z 分量的实数部分,Re(Ez)Fig.10.Topological transition of phonon polaritons in the twisted bilayer α-MoO3.[83] (a) Schematic diagram of the twisted bilayer α-MoO3.The [100] and [001] directions of the bottom α-MoO3 are defined as the x and y axes,respectively.The twist angle Δθ is defined as the counterclockwise rotation angle of the top layer α-MoO3 relative to the bottom layer.(b)–(e) and (j)–(m) Near-field optical images reflecting the topological properties of the phonon polariton dispersion as a function of the twist angle at a frequency of 916 cm–1 (Fig.(b)–(e)) and 986 cm–1 (Fig.(j)–(m));(f)–(i) and (n)–(q) corresponds to calculated real parts of z-components of the electric field distributions,Re(Ez).
考虑到石墨烯的能带可调控的特性,通过石墨烯界面工程构建二维堆叠异质结构是一种动态调控层间耦合以实现光学拓扑转变操纵的新策略.2022 年,Zeng 等[84]通过模拟计算发现在石墨烯和α-MoO3堆叠的异质界面结构中,调节石墨烯费米能级和α-MoO3的厚度分别可以实现杂化极化激元的椭圆和双曲线之间的转变.同年,Hu 等[85]在实验上实现了通过改变费米能来调控“石墨烯/α-MoO3/衬底”结构的极化激元的拓扑转变.该团队还发现,在红外光910 cm–1的波数下,石墨烯/α-MoO3结构在Au 衬底上比在SiO2衬底上更容易实现调控,即更低的费米能即可实现双曲线到椭圆的极化激元的转变.
6.2 转角三层黑磷的双曲极化表面
α-MoO3成功演示了天然二维原子晶体中支持双曲声子极化激元,并且双层转角可以调控极化激元从双曲向椭圆的拓扑转变,致使研究人员开始寻找更多介电函数各向异性的天然二维原子晶体[71,86].黑磷具有范德瓦耳斯层状结构,其二维原子晶体具有很强的面内各向异性[87−92],并且被预言有希望支持双曲型等离激元和激子极化激元[70,71].目前已报道关于黑磷极化激元包括薄层、叠层及转角的研究大多是基于理论和模拟的结果.
Zheng 等[93]用模拟的方法演示了三层黑磷通过转角来调控其极化激元双曲线的形态.转角双层双曲材料实现从开放(双曲型)到闭合(椭圆型)的拓扑转变必须满足单层大于45°的开放角的条件.当开放角小于45°时,无论转角如何,都不能实现闭合拓扑.通过三层堆叠就可以使从开到闭的拓扑转变条件降低到开放角大于30°.例如,单片黑磷双曲线在1900 cm–1处的开放角为38.2°,在该频率下,由于开放角小于45°,开放到关闭的拓扑转变无法实现,然而,通过引入第三层黑磷可以激活这种拓扑转变[93].多层堆叠可以在更多的频率范围里灵活地控制色散,从而扩展了从开到关转换控制的可用带宽.
7 转角石墨烯的手性等离极化激元
当物体的镜像并不等于其自身时,它就具有手性.手性材料在偏振光学、立体化学和自旋电子学等领域有着重要应用.扭转角为θ与–θ的双层石墨烯并不具有完全相同的结构,转角会引起整体反演对称性的破缺,从而产生手性.转角双层石墨烯布里渊区中K和K′谷处能带具有方向相反且非零的Berry 曲率,当载流子处于该(K或K′)能带中时会获得一个非经典的横向速度.谷极化会产生非零Berry 通量,从而引起无磁场的手性等离激元激发[10,94].早在2016 年,Song 等[94]预言了在间隙狄拉克材料(gapped Dirac materials)中,净Berry 曲率可导致手性等离激元模式.2018 年,Stauber 等[95]在理论上研究了转角双层石墨烯的等离激元模式以及与纵向磁矩相关的手性特征.2020 年,Lin 等[96]在考虑了转角双层石墨烯层间量子耦合条件下,求解了其手性等离激元的全麦克斯韦方程的一般解,发现转角双层石墨烯可以等效为一个同时具有手性、磁学、电学表面电导率的手性超表面.此后,Stauber 等[97]和Margetis 等[98]也分别对转角双层石墨烯的手性等离激元进行研究,结果表明转角双层石墨烯的手性等离激元可以通过表观纵向磁矩来反映,且与远场圆偏振光相比,等离激元可增强其近场手性.
在实验方面,Kim 等[99]将生长的单层石墨烯单晶薄膜以扭转角θ堆叠制备手性转角双层石墨烯,并首次通过圆二色谱表征其手性特征,获得了较高的椭圆度值(6.5(°)/µm).Huang 等[10]在具有莫尔纹超晶格的转角双层石墨烯中,采用无磁场的圆极化红外光谱观察到了手性等离激元模式.在这项研究中,通过构建螺旋状石墨烯等离激元谐振器以及光谱特征峰比对的策略,观测到了转角双层石墨烯中的手性等离激元对应的特征分裂吸收峰,以及手性等离激元对光强度和电子填充的依赖性.手性等离激元模式展示了小角度下转角双层石墨烯中一种新的量子光学特性.
8 总结与展望
本文从扫描近场光学显微技术、叠层/转角二维原子晶体样品的制备、以及各种光学结构和极化激元性质等方面介绍了极化激元纳米光子学领域的重要进展.这些研究进展为二维光电子学的发展带来新的可能,同时为未来高性能纳米光子器件的研制提供基础和丰富的材料储备.
石墨烯是研究二维等离激元和用于调控叠层异质材料极化激元的重要材料,也是本文重点介绍的材料.石墨烯具有很高的等离激元波长压缩比,是传统金属的数十倍,这使得石墨烯具有制备纳米尺度光子器件的巨大潜力,如纳米光波导、全光逻辑器件等.转角石墨烯结构中出现的莫尔超晶格和周期性孤子网络图案,有望成为构筑无光刻二维等离激元光子晶体的重要手段;在三层石墨烯中,ABA 和ABC 堆叠的结构可以组成金属-半导体面内异质结,且异质界面极易操控,可为纳米光电子器件的发展提供支持.另一方面,石墨烯具有非常高的载流子迁移率和远低于金属的载流子浓度,使得其等离激元可以实现从近红外到太赫兹波段极宽频段的调控.在石墨烯/α-MoO3异质结构中,石墨烯可控的费米能,更易于调控其极化激元的拓扑转变.除此之外,转角石墨烯手性等离激元、转角α-MoO3的双曲极化激元的拓扑转变等奇特物理特性也为微纳光电器件设计带来了新的机遇.比如,利用手性特性制备无磁场的法拉第旋转器、单向波导等新型光子器件,或利用超表面特性开展变换光学理论研究以及制作光学隐身衣、超透镜等装置.
除了本文涉及的石墨烯、hBN、α-MoO3、黑磷外,对于其他二维材料,如过渡金属硫族化合物等,在不同堆叠/转角下也有望观测到新的极化激元特性.例如,过渡金属硫族化合物异质结中存在莫尔激子以及维格纳晶体等行为[100−102],在其中可能涌现出莫尔激子极化激元;在魔角石墨烯中发现了超导现象[103−106],可能存在库珀对极化激元;对于磁性二维材料,可存在磁振子极化激元等.这些材料通过不同的堆叠次序以及不同转角的组合,有望产生更丰富的极化激元新模式及耦合行为,并涌现出新的光电现象.总之,转角/叠层二维原子晶体作为一类支持极化激元的天然光子晶体,为纳米光子学领域研究提供了新的平台,并将继续成为未来材料学与物理学最前沿的研究热点.

