基于ARWLS和AUKF的锂电池SOC估计

周 琴，沈 辉，孙明珠，陈正荣，徐鹏程

基于ARWLS和AUKF的锂电池SOC估计

周 琴1，沈 辉1，孙明珠2，陈正荣1，徐鹏程1

（1.扬州大学，江苏 扬州 213000；2.合肥职业技术学院 汽车工程学院，安徽 合肥 238010）

精确估计锂电池荷电状态（SOC）对纯电动汽车的安全稳定行驶有着深远影响，对锂电池SOC状态的估计主要有参数辨识算法和SOC估计算法两个热点问题。针对辨识过程中出现的“数据饱和”现象以及锂电池SOC状态估计时的滤波发散问题，文章提出了自适应遗忘因子递推最小二乘法（ARWLS）-自适应无迹卡尔曼滤波（AUKF）联合算法。首先建立了二阶R-C锂电池数学模型，并针对传统最小二乘法在参数辨识过程中出现的“数据饱和”现象，引入了自适应遗忘因子动态修正新旧数据权重，提升在线参数辨识的准确度以及效率。其次，针对无迹卡尔曼滤波存在的滤波失效问题，提出了自适应无迹卡尔曼滤波算法来自适应调整系统噪声和观测噪声，从而提高SOC估计时的适应性和鲁棒性。最后在混合动力脉冲能力特性（HPPC）工况下对扩展卡尔曼滤波（EKF）、无迹卡尔曼滤波（UKF）和AUKF三种SOC估计算法进行仿真比较，仿真结果表明，AUKF算法估计的SOC曲线跟随SOC真实值曲线变化的性能最好，估计精度也优于其他两种算法，具有更小的估计误差，收敛性也最好。

锂电池；荷电状态；在线参数辨识；ARWLS；AUKF

目前的环境危机和能源危机严重制约着燃油汽车产业的发展。近年来，各国政府加大了对纯电动汽车的研发力度，未来汽车的发展趋势是电动化、智能化、共享化以及网联化。动力电池作为电动汽车的核心部件之一，其技术发展直接决定了电动汽车的发展前景。锂电池具有重量轻、储能大、功率大、无污染等特点，开始被广泛应用于电动汽车上；但锂电池单体电压、温度及电流过大或过小都严重影响电池性能，高效可靠的电池管理系统（Battery Management System, BMS）被用来满足其安全需要、延长电池使用寿命[1]。

BMS是动力电池工作时的“中枢神经”，对单个电池的运行工况信息进行检测，再将检测到的信息通过控制器局域网络（Controller Area Network, CAN）传输到BMS的主控制器进行相应的操作，最后将动力电池运行参数信号发送到整车控制器和电机控制器，并且将动力电池运行参数信号发送到状态监测模块，让用户能实时掌握每节电池的状态；BMS可以采集动力电池组的单节电池电压、温度以及电流等一些可以直接测量的外部状态，通过特定算法来估计动力电池中不可测量的内部状态，如荷电状态（State Of Charge, SOC）、电池的健康状态（State Of Health, SOH）、充放电功率等[2]。其中SOC用来表征动力电池剩余电量，直接反映出车辆续航里程，有效防止电池过充或过放，达到延长电池使用寿命及提高续航能力的目的，SOC监测对电动汽车安全可靠行驶有着十分重要的作用，但SOC是电池内部状态，需先建立电池模型进行参数辨识，再运用合适算法估计电池SOC[3]。

在建立电池模型进行参数辨识算法方面，当确定模型结构之后，需要获得模型参数，电池在实际使用过程中，在不同SOC、不同温度、不同电流以及不同老化条件下电池的模型参数是不一样的，离线辨识的模型参数是不变的，电池工作时真实情况无法被精确反映，因此，该模型精度是不够的。针对离线参数辨识存在的问题，有学者提出了在线参数辨识，例如递推最小二乘法[4]（Recursive Least Squares, RLS）。RLS的出现，虽然解决了传统最小二乘法在参数辨识时时效性不够的问题，但也出现了新的问题，系统参数随着时间递推较久后，新加入的数据无法正常修正辨识结果，出现“数据饱和”现象[5]。刘志聪等[6]采用带遗忘因子的递推最小二乘法（Forgetting Factor Recursive Least Squares, FFRLS）的参数在线辨识来解决RLS带来的“数据饱和”问题，算法的追踪效果得到了很大改进，但遗忘因子固定不变，需自己选取。

在锂电池SOC估计方面，常用的方法有安时积分法、神经网络法、开路电压法和卡尔曼滤波法。其中，卡尔曼滤波算法的研究最多。田元武等[7]针对锂电池SOC估计精度低的问题，提出了自适应拓展卡尔曼滤波算法将SOC计算误差控制在2%以内，提高了估算精度和鲁棒性。邢丽坤等[8]提出了多新息无迹卡尔曼滤波算法进行SOC估算，并在城市道路循环（Urban Dynamometer Driving Schedule, UDDS）工况下将SOC误差控制在1.08%左右，验证了算法的有效性。

基于上述分析，在锂电池模型参数辨识和SOC估计方面，FFRLS在参数辨识方面虽然解决了“数据饱和”现象，但是遗忘因子没法自动调整，算法适用性不高；在SOC估计时，由于锂电池是强非线性系统，且存在系统噪声和观测噪声的干扰，很大程度上影响了SOC的估计精度。因此，本文提出了自适应遗忘因子递推最小二乘法（Adaptive Recursive Weighted Least Square, ARWLS）-自适应无迹卡尔曼滤波（Adaptive Unscented Kalman Filter, AUKF）联合算法，在参数辨识过程中引入了自适应遗忘因子动态修正新旧数据权重，提升在线参数辨识的准确度以及效率，在SOC估计时提出了AUKF算法来自适应调整系统噪声和观测噪声，解决了滤波失效问题，从而提高SOC估计时的适应性和鲁棒性。最后在混合动力脉冲能力特性（Hybrid Pulse Power Characterization, HPPC）工况下对扩展卡尔曼滤波（Extended Kalman Filter, EKF）、无迹卡尔曼滤波（Unscented Kalman Filter, UKF）和AUKF三种SOC估计算法进行仿真比较。不难发现，ARWLS- AUKF算法估计的SOC曲线跟随SOC真实值曲线变化的性能最好，估计精度也优于其他两种算法，具有更小的估计误差，收敛性也最好。

1 锂电池数学模型的建立

在常用的电池等效模型中，等效电路模型能很好表现出锂电池内部状态中复杂的化学反应。常见的等效电路模型有Rint模型、Thevenin模型、PNGV模型和高阶动态模型[9]。高阶动态模型相对其他模型更加复杂，模型中除了包含电池电压和内阻特性外，还考虑了内部的扩散和极化反应。研究表明，电池模型刻画电池内部的扩散和极化反应的精确度和阶数有关，阶数越高，辨识的精度会越高，但需要辨识的参数也会随之增加，导致需要计算的数据量增加[10]。综合来看，二阶R-C模型更加适用于模拟电池的工作特性，作为建立动力电池数学模型的首选，二阶R-C等效电路模型如图1所示。

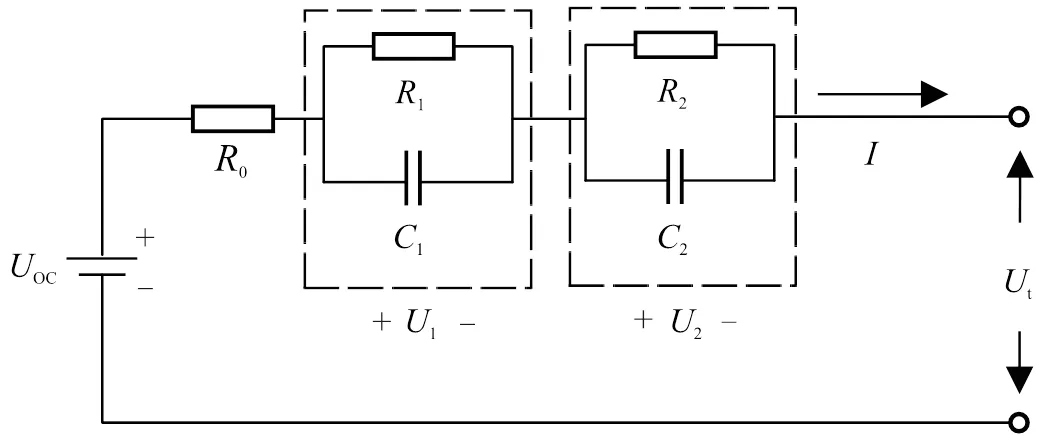
图1 二阶R-C等效电路模型

运用基尔霍夫电压定律和基尔霍夫电流定律对该回路求解来得到函数表达式：

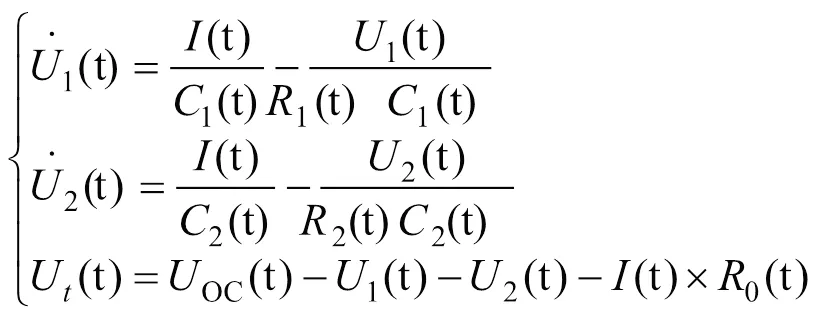
式中，oc为电池开路电压，由电池SOC确定；0为电池欧姆内阻；1、2为电池极化电阻；为电池工作时充放电电流，由传感器测得；t为电池端电压，由传感器测得；1、2为电池极化电容；1、2为R-C回路电压。

通常将SOC定义为电池剩余容量与额定容量之比，比值为0～100%。SOC表达式为

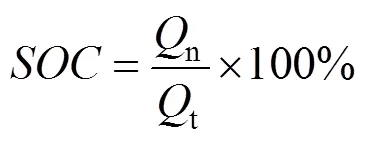
式中，n、t为剩余容量和额定容量。

将式（2）进行离散化处理后的表达式如下：

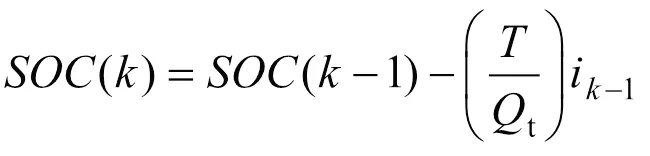
式中，()为时刻SOC值；为充放电时间。

联立式（2）和式（3），可以得到模型的状态空间表达式为

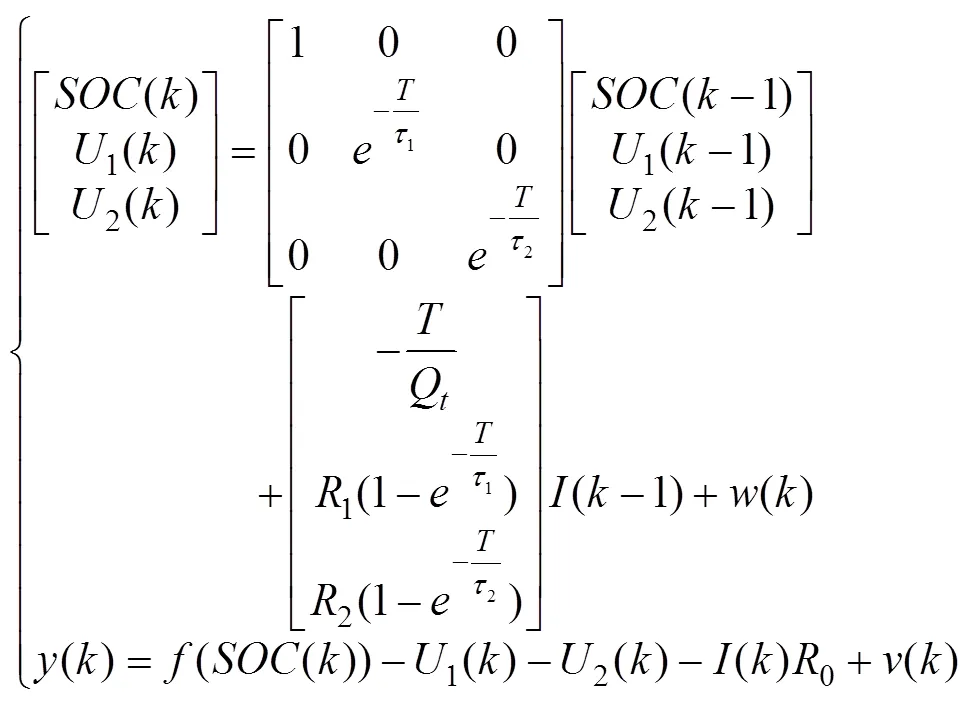
式中，选择[1()2()()]T为三维状态变量；t为输出量；为输入量；=，为时间常数；()为系统噪声；()为观测噪声；()、()均满足正态分布，属于高斯白噪声。

锂电池开路电压（Open Circuit Voltage, OCV）与SOC之间的关系很大程度上影响了SOC估算。为了得到较为准确的OCV-SOC曲线，采用HPPC实验对电池进行脉冲放电[11]。具体步骤如下：

（1）在室温25 ℃时，用1 C倍率给锂电池恒流充电到4.2 V，恒压充电到<1.5 A，即断电静置1 h；

（2）以0.2 C倍率进行放电到锂电池SOC减小了5%，停止放电静置1 h，把此时的oc记录下来；

（3）重复上个步骤，直到锂电池的SOC降到5%。将记录的OCV-SOC数据整理如表1所示。

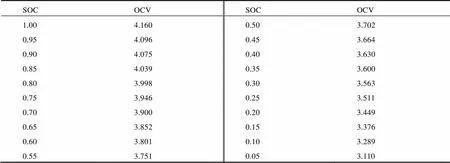
表1 不同SOC下的Uoc值

把表1数据进行9次多项式拟合，得到拟合后的开路电压OCV-SOC的非线性曲线，如图2所示。

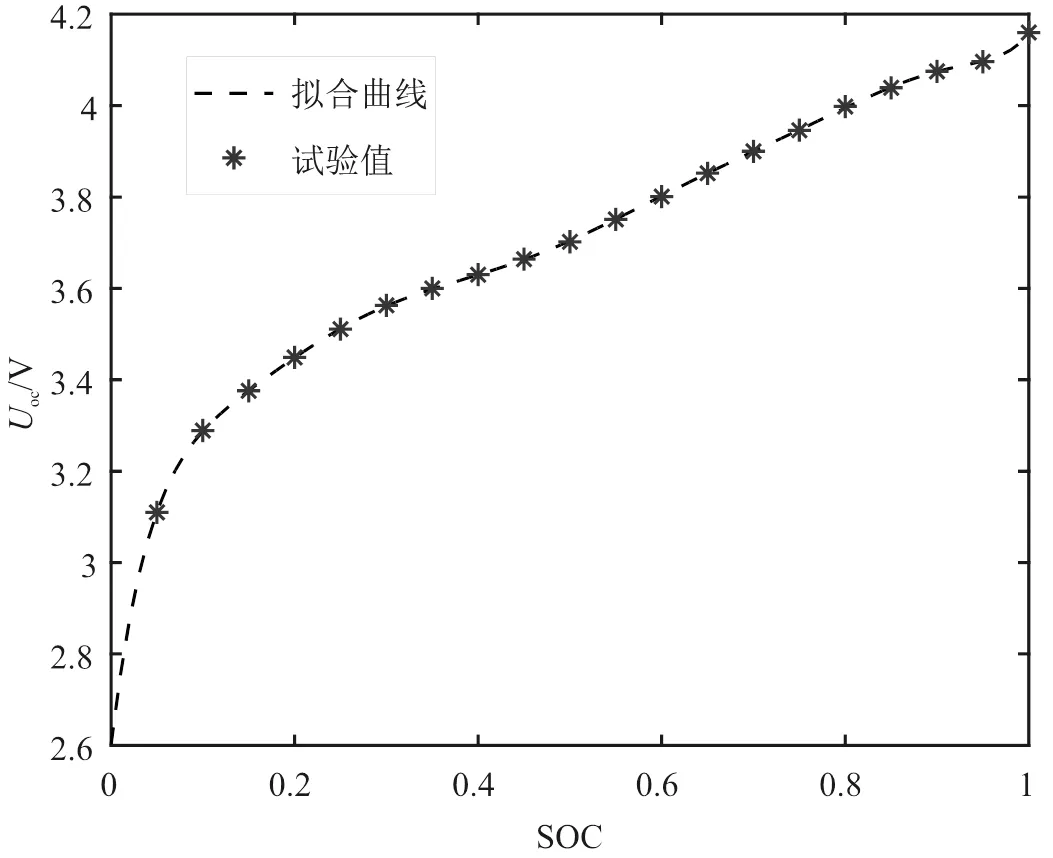
图2 OCV-SOC曲线（九阶）

拟合好后的曲线表达式如下：

2 电池模型的参数辨识

电池模型参数辨识分为离线和在线辨识[12]。为得到较准确结果，离线辨识需进行大量测试，离线辨识无法跟随电池实际运行工况做出实时调整[13]。为解决离线辨识存在问题，引入在线估计参数方法，把模型参数更新到电池里面去，可以实时跟踪当前电池参数。在线辨识是BMS在运行过程中用当前测得的电压数据及历史工况，用合适算法把模型的参数估计出来。本文将FFRLS中的遗忘因子改成可变化的，变成ARWLS算法，该算法解决了系统参数随着时间递推较久后，新加入的数据无法正常修正辨识结果的“数据饱和”现象，同时可变的遗忘因子可以动态修正新旧数据权重，大大提升了在线辨识的准确度以及效率。ARWLS的迭代公式如下：

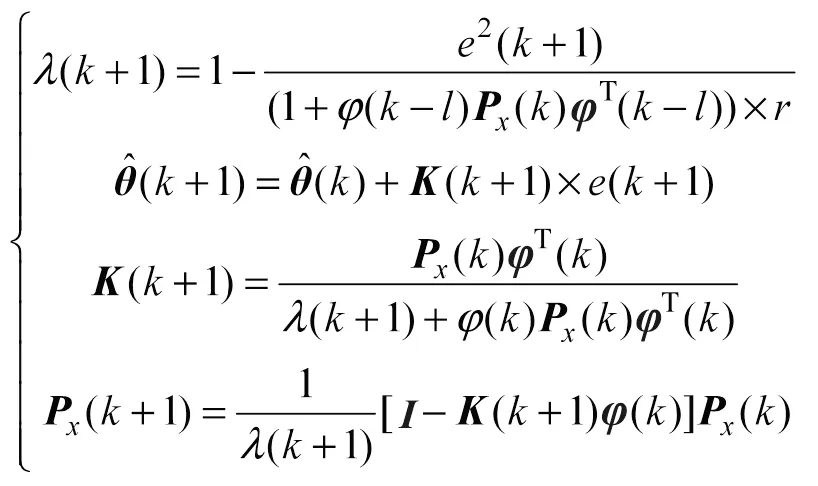
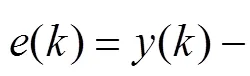
对式（1）使用ARWLS算法进行拉氏变换，得到域上的传递函数：

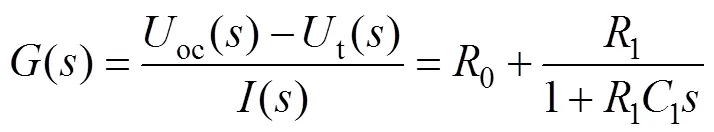
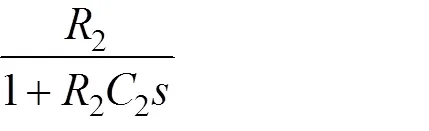
令：

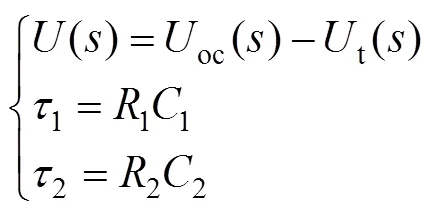
将式（7）和式（8）进行联立可以得到

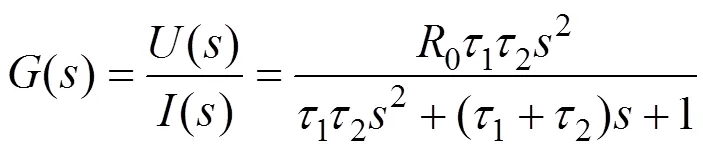
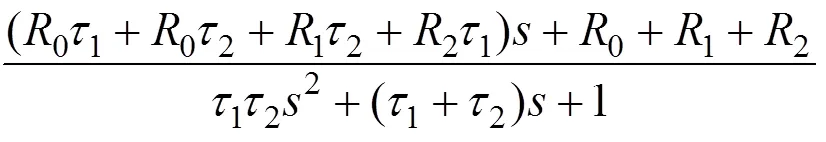
再令：

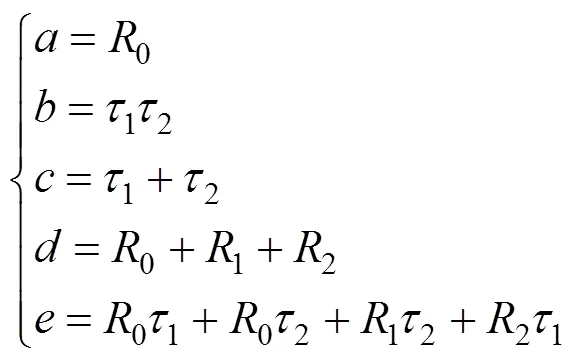
将式（10）带到式（9）中可以得到表达式为

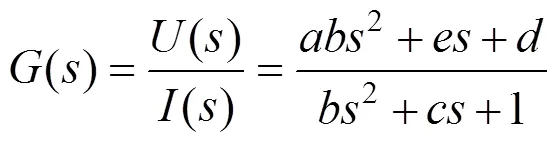
根据式（12）对式（11）进行变换，来保证系统在离散化时的一致性为

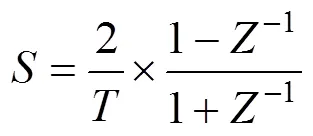
其中，为变换算子，其中=e.s，可以得到域上传递函数表达式为

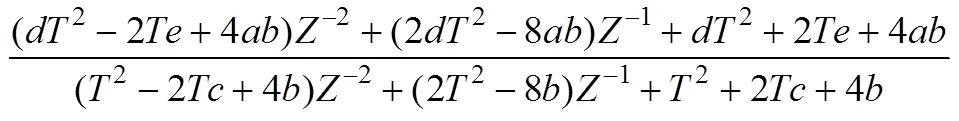
再令：

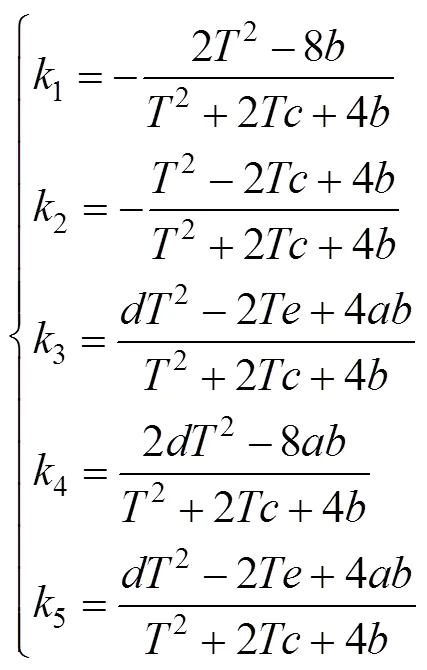
根据式（13）和式（14）可得

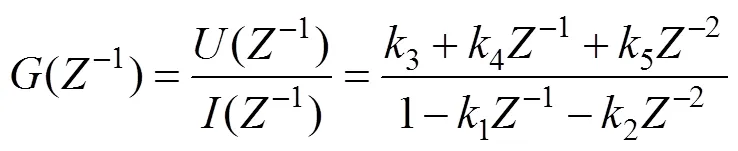
根据式（15）可得出差分方程为

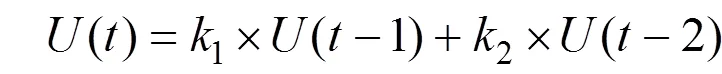
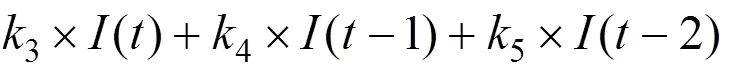
再令：

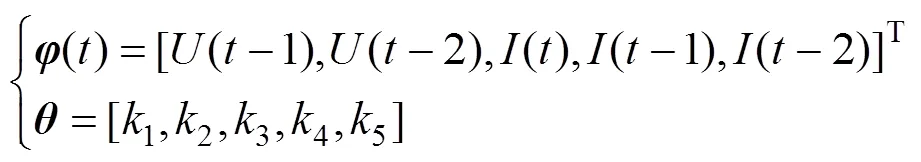
则

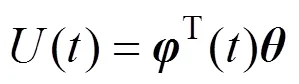
由式（14）可以求出，，，，的值：

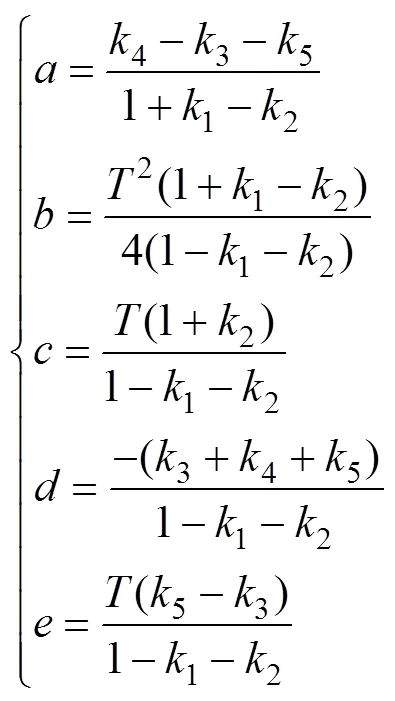
由式（10）和式（19）求出0，1，2，1，2的值为

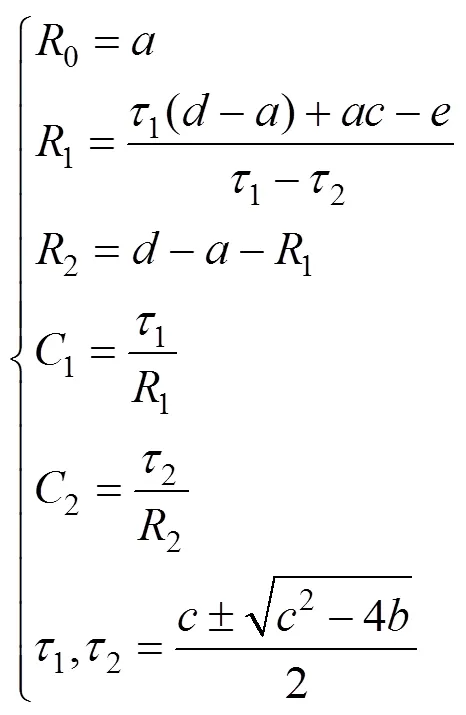
本文在线辨识采用HPPC工况，ARWLS算法在线辨识时SOC初始值为90%，输入和输出分别是该工况下电压和电流，辨识结果如图3—图5所示。

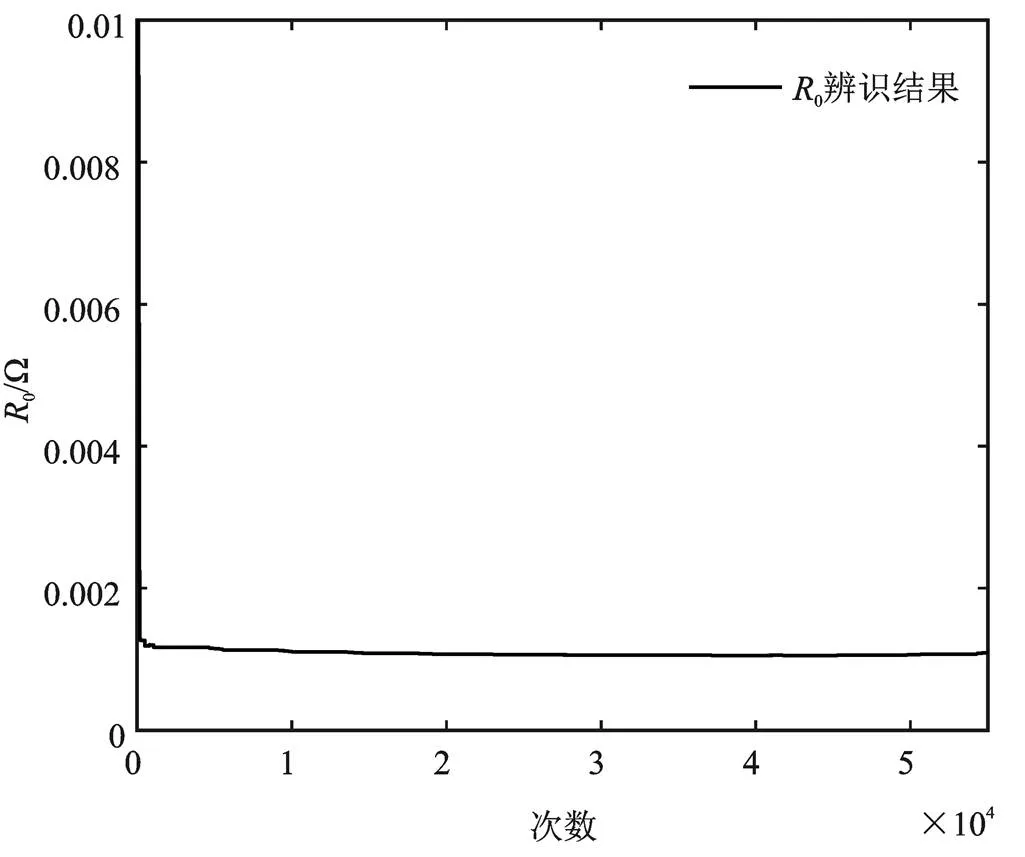
图3 欧姆内阻R0辨识结果

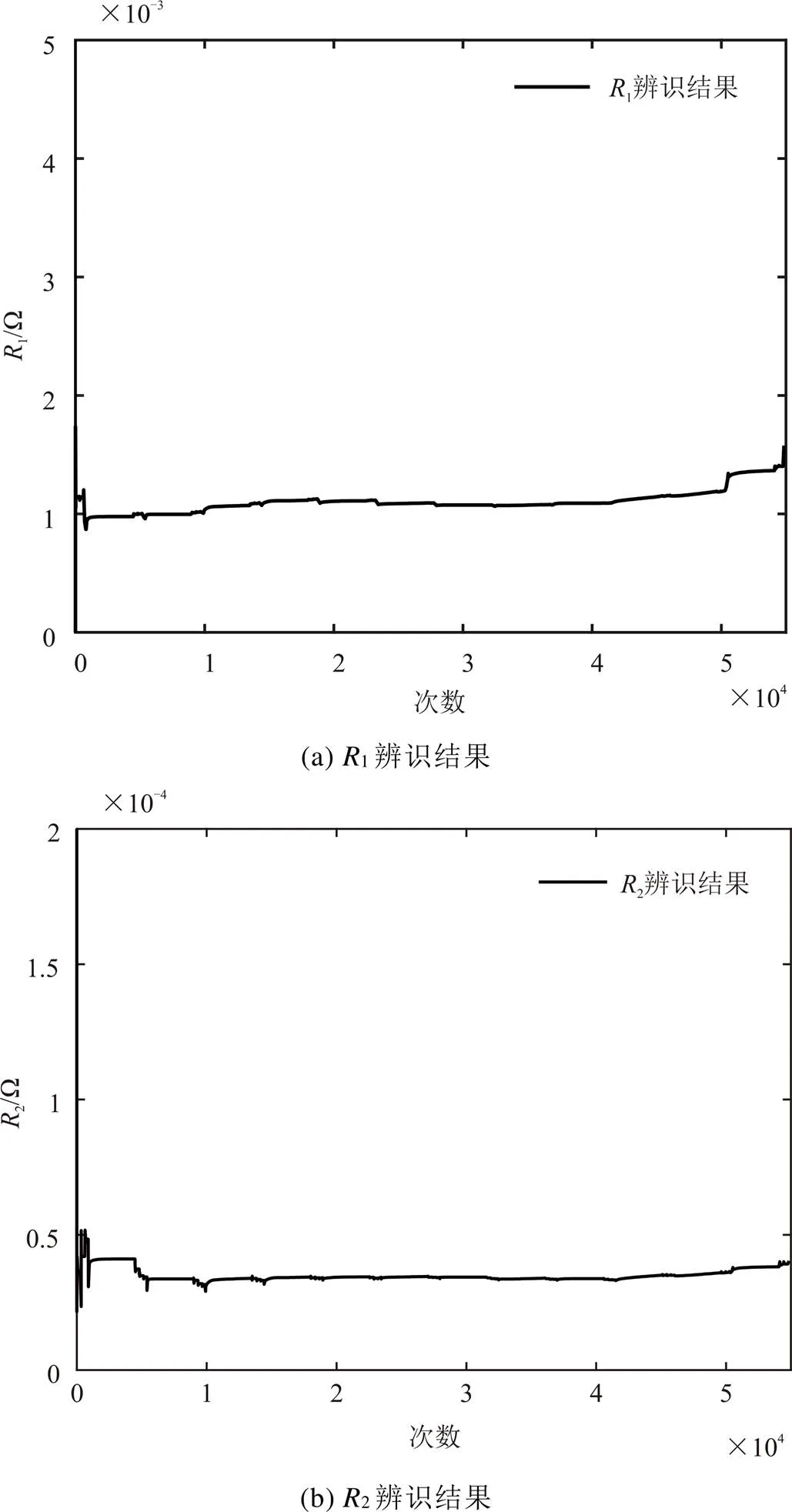
图4 极化内阻辨识结果

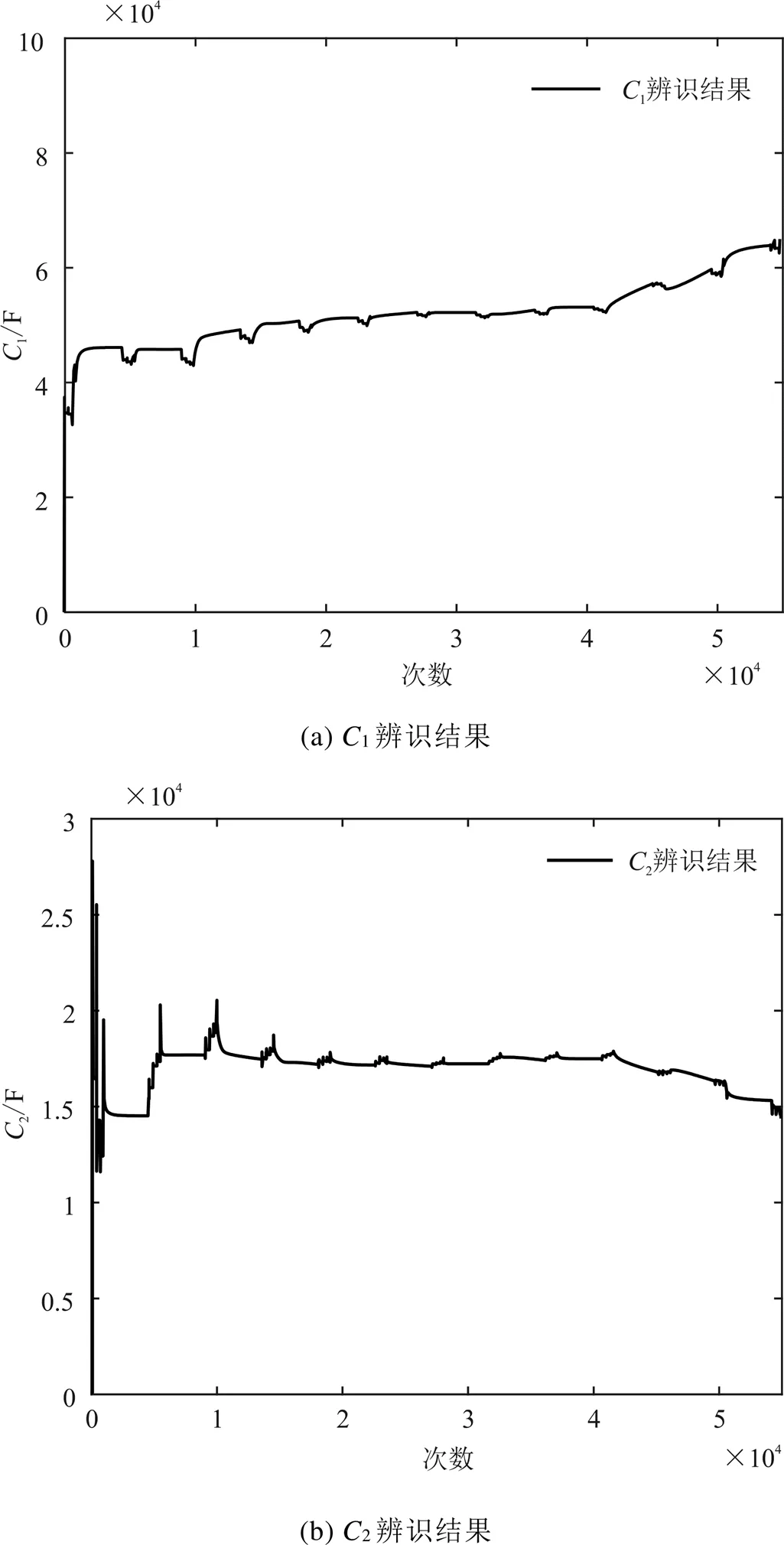
图5 极化电容辨识结果

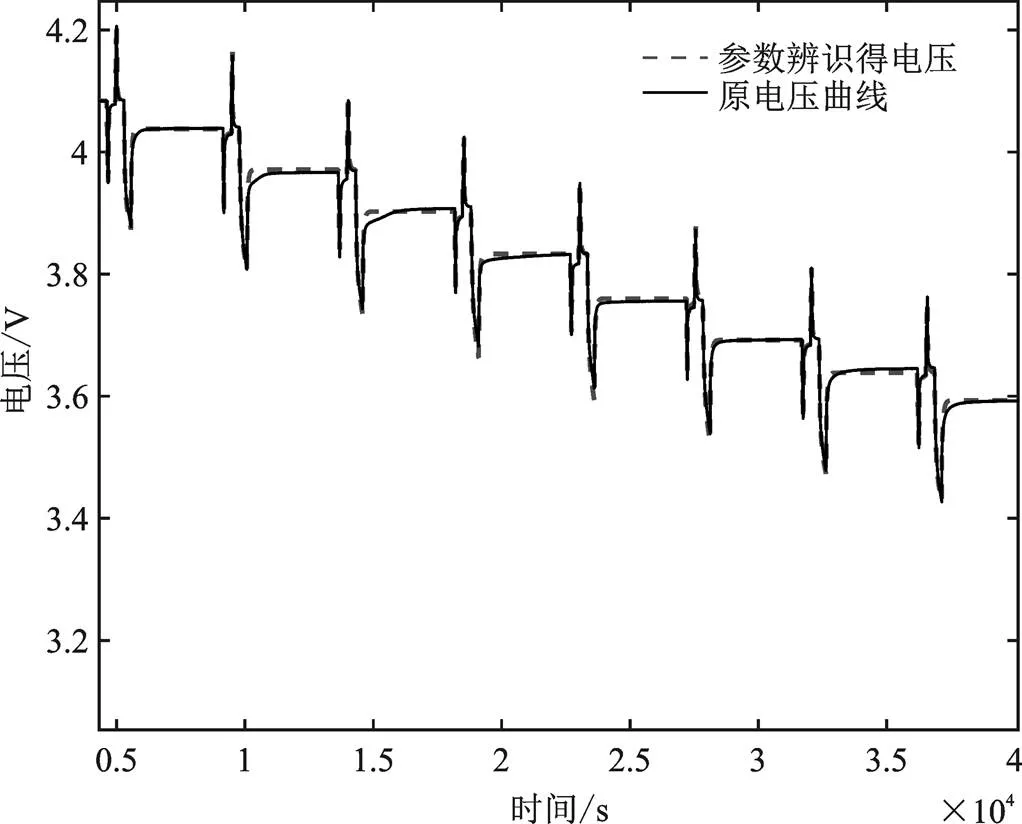
图6 参数辨识电压与原电压对比图

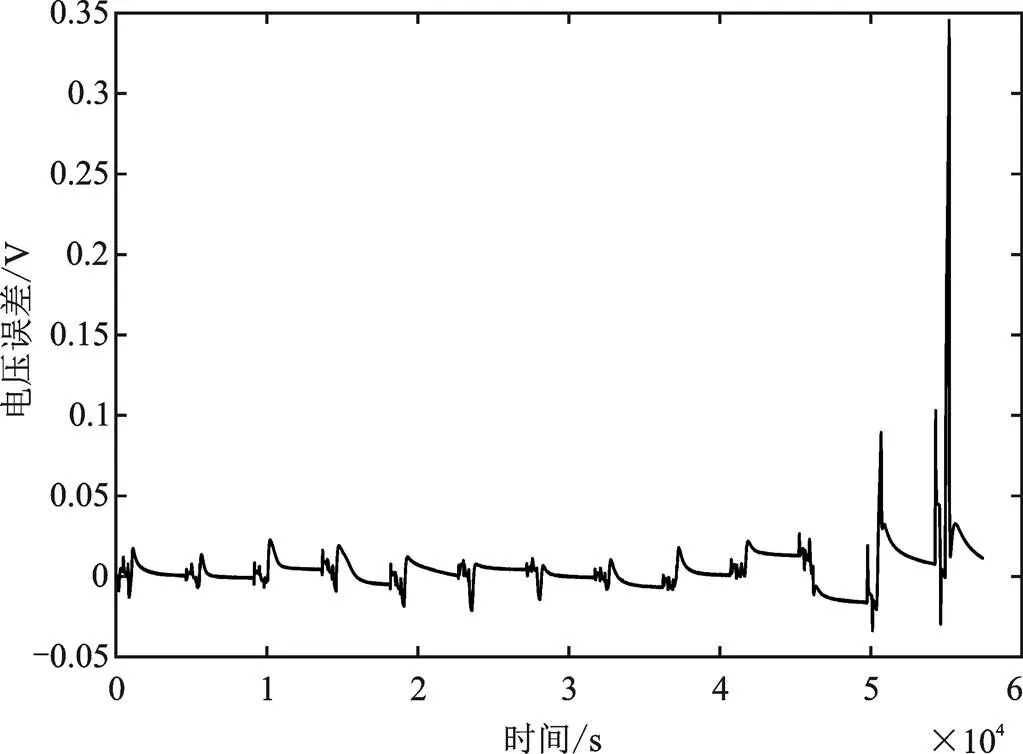
图7 模型误差图

锂电池经过参数在线辨识后将等效电路模型的各参数辨识出来后，还需要验证辨识结果的正确性，将HPPC工况下的电流加到等效模型中，再把辨识出来的0，1，2，1以及2加载到模型中，对比仿真参数辨识后的端电压和原电压如图6所示，电压误差如图7所示。

通过参数辨识后的端电压和原电压对比可以看出，因为设置的各参数初值不够准确，使得一开始参数辨识后的端电压和原电压误差较大，随着时间的推移，算法使误差在慢慢缩小。后面的电压误差变大属于正常现象，因为在SOC较低时，放电电压会有比较剧烈的跳变。结果表明，提出ARWLS对锂电池在线参数辨识结果是正确的，算法也有效，为后文锂电池SOC估计提供了高精度等效电路模型。

3 联合算法在线估算SOC

3.1 UKF算法原理

卡尔曼滤波算法[14]通常被用来处理线性高斯系统，该算法利用最小均方差准则对系统状态空间中的系统噪声和观测噪声进行滤波，从而将状态变量中的最优结果估算出来。一般在时域范围内对卡尔曼滤波算法进行分析，其估算过程的核心是“预测+校正”的迭代滤波过程，即使用上一次的状态估计以及系统的动态方程对当前的状态进行一个预测，得到当前时刻的预测值，再根据采样得到的测量值来校正当前时刻的测量值，得到最优结果。但无法适用于类似锂电池这样的非线性系统中。

为了解决在非线性系统中的适应性问题，有学者提出了EKF算法，将状态表达式中的非线性部分进行泰勒级数展开并近似线性化处理，再使用EKF进行“预测+校正”的迭代滤波得到最优估计值。然而EKF在近似线性化处理过程中没考虑高阶项误差，使EKF在高度非线性系统应用中滤波结果发散，降低算法鲁棒性，同时EKF需要计算较为繁琐的雅克比矩阵，只有在状态方程和观测方程都接近线性且连续时，EKF才能最终较好地收敛于全局最优。为了进一步提升算法适用性，有学者提出了UKF算法，该算法的关键是采用了UT变换，UT变换的核心是根据当前时刻的状态变量的均值和方差，按照某种采样规则选取一定的采样点，然后对构造的每个采样点进行非线性变换，得到变换后新的点集，以及变换后点集的均值和方差。UKF算法利用UT变换在估计点附近进行采样，将选取一个状态估计点转换成选取多个估计点，再依据权重的差别，把状态估计点的值给下一时刻的观测值，根据观测值和测量值的误差，通过将对应的权重进行反馈校正，来达到逼近非线性函数的概率密度分布的目的，这样就没有了对状态表达式中的非线性部分进行近似线性化处理，并且无需复杂求导，这使得非线性变换具有更高精度的均值和协方差，有效克服了EKF估算精度较低，应用于高度非线性系统时稳定性差等不足，可得到更加理想的最优估计值。

UKF算法具体实现过程由系统初始化、Sigma点集计算、状态预测以及测量更新四个部分组成。

1.系统初始化

状态量、误差协方差初始化表达式为

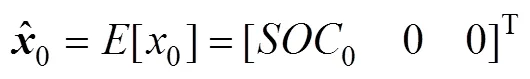
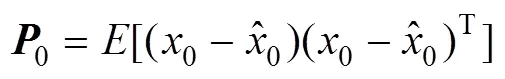
2.构建Sigma点集

根据输入状态变量的统计值和，采用构造2+1个Sigma点的对称采样策略，每个采样点与状态变量具有相同的统计特性：

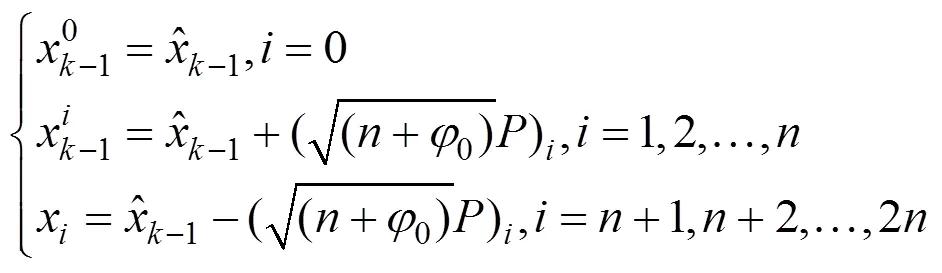
式中，0为尺度参数；为扩展状态变量维数，这里=3，表示电池SOC极化电压1和2。

3.状态预测

为实现对状态变量的预测，使用Sigma点的预测进行加权平均表达式为

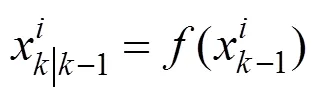
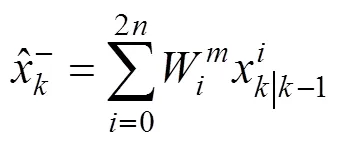
将Sigma点集代入观测方程对状态量和误差量进行新的观测表达式为

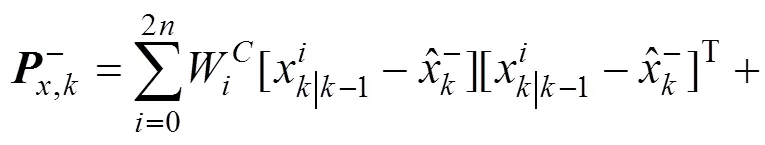
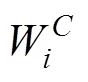
4.测量更新

时刻估计的观测量表达式为

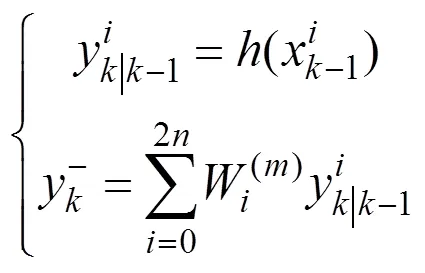
时刻观测量的方差矩阵表达式为

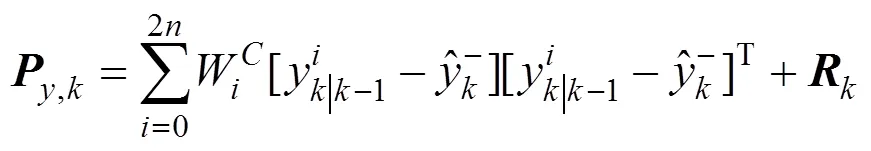
式中，为观测噪声协方差矩阵。

时刻状态量和观测量协方差表达式为

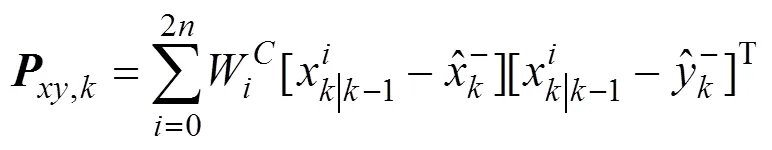
卡尔曼增益表达式为

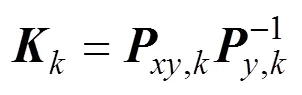
状态量和误差方差矩阵更新表达式为

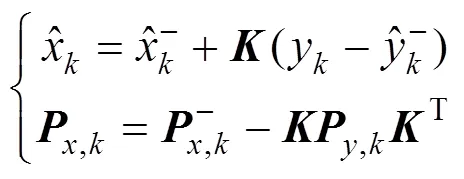
3.2 AUKF波算法原理

UKF算法的实现是基于对噪声的理想假设，通常会把系统模型的噪声假设成服从正态分布的高斯白噪声。但系统模型噪声会随时间变化，不是完全已知。因此，用UKF估计SOC状态存在以下问题：

（1）由于锂电池模型作为高度非线性化的系统会由很多干扰因素，这样就无法得到准确的系统噪声协方差矩阵和观测噪声协方差矩阵，通过先验估计初始化两个协方差矩阵会降低算法精度。

（2）UKF算法的精度很大程度上取决于电池模型的精度，在电池等效模型参数辨识过程中对电池参数的辨识是无法做到很准确的，因此，观测噪声协方差矩阵取值不当或者电池模型存在很大误差时，就会在观测校正时引入较大误差。

（3）电池在使用过程中，若是出现突发情况会有观测噪声的干扰，导致SOC精度估计不够准确，严重时会有短时失真现象。

在上述情况下，UKF估计SOC状态时可能会出现滤波失效现象，本文提出了AUKF算法，AUKF算法与UKF算法相比，搭建的状态空间模型基本相同，不同点是AUKF可以去自适应调整系统噪声协方差和观测噪声协方差。具体做法如下：

（1）将实时测量电压和模型预测电压定义成残差ε，其表达式如下：

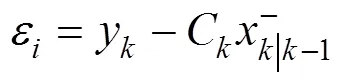
（2）利用定义的新息，对系统噪声协方差和观测噪声协方差进行实时修正；

（3）再将实时修正后的系统噪声协方差和观测噪声协方差代到状态空间方程中修正电池状态，和估计更新递推方程为

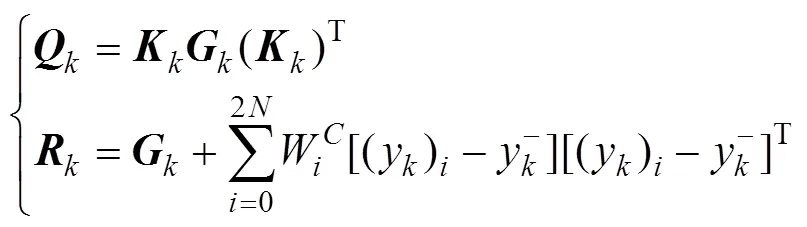
为残差组成的协方差近似值，表达式为

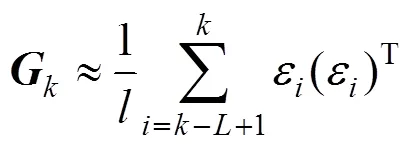
式中，为ε序列长度。

使用ARWLS和AUKF联合算法估计SOC的流程图如下：

为了验证本文所提出算法的有效性和准确性，使用HPPC工况进行仿真实验，SOC初始化都为1。图9为不同算法的SOC对比图，图10为不同算法的误差对比图。

从图9和图10中不难看出，本文使用的EKF、UKF和AUKF算法均可以较快向真实的SOC值附近收敛，但比较三种不同算法，可以看出收敛效果最好的是AUKF算法，使用AUKF算法估算的SOC曲线几乎和真实的SOC值相吻合。EKF和UKF算法的估计误差很大程度上都控制在2%左右，但EKF算法的误差曲线有较大的波动，最大误差为3%，相较于EKF算法，UKF算法的误差曲线波动小了很多，最大误差也只有2%，说明SOC估算精度得到进一步提高。AUKF算法估计曲线波动较小，曲线平滑与真实值曲线几乎一致，并且误差曲线一直维持在0附近，累计误差很小，说明本文提出的AUKF算法估计性能要优于上述两种算法，具有更小的估计误差，收敛性最好。

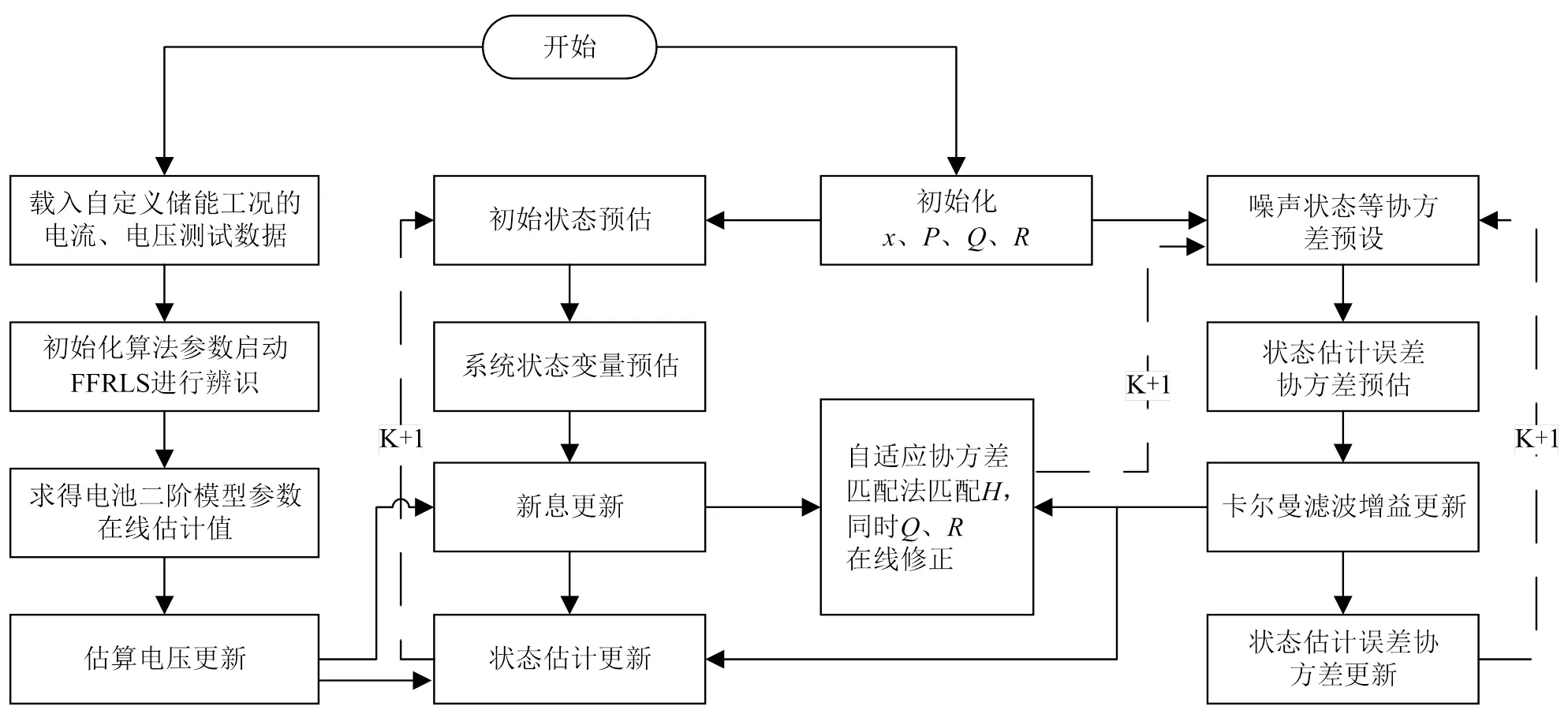
图8 ARWLS+AUKF联合算法流程图

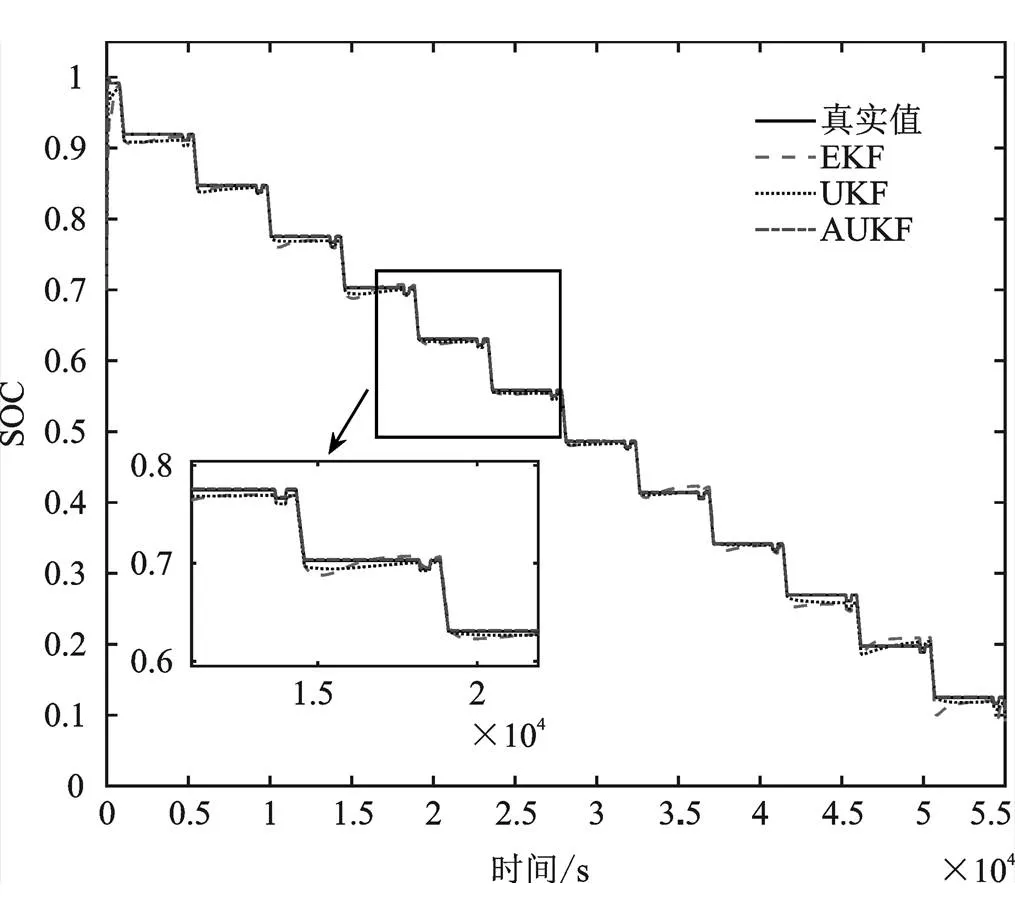
图9 不同算法的SOC对比

图10 不同算法的误差对比

4 结语

本文首先建立锂电池二阶R-C等效电路数学模型来模拟电池的工作特性，采用HPPC实验来获得锂电池的开路电压OC。接着采用ARWLS算法将锂电池等效电路模型的各参数辨识出来，通过对比仿真参数辨识后的端电压和原电压来验证其算法的有效性。最后提出了自适应无迹卡尔曼滤波算法来自适应调整卡尔曼增益、系统噪声和观测噪声，在HPPC工况下对EKF、UKF和AUKF三种SOC估计算法进行仿真比较。相较于另外两种算法，ARWLS-AUKF算法估计的SOC曲线跟随SOC真实值曲线变化的性能最好，估计精度也优于其他两种算法，具有更小的估计误差，收敛性也最好。

[1] 缪平,姚祯,LEMMON J,等.电池储能技术研究进展及展望[J].储能科学与技术,2020,9(3):670-678.

[2] 王彪.电动车电池管理系统研究与设计[D].太原:中北大学,2022.

[3] ASLAN E, YASA Y. A Review on the Battery State of Charge Estimation Methods for Electric Vehicle Battery Management Systems[C]// 2019 11th Interna- tional Conference on Electrical and Electronics Engineering. Piscataway:IEEE,2019:281-285.

[4] LIU G, XU C, JIANG K,et al. State of Charge and Model Parameters Estimation of Liquid Metal Batteries Based on Adaptive Unscented Kalman Filter[J].Energy Procedia,2019,158:4477-4482.

[5] LI X,WANG Z,ZHANG L.Co-estimation of Capacity and State-of-charge for lithiumion Batteries in Electric Vehicles[J].Energy,2019,174:33-44.

[6] 刘志聪,张彦会.锂离子电池参数辨识及荷电状态的估算[J].储能科学与技术,2022,11(11):3613-3622.

[7] 田元武,张诗建,周博雅,等.基于ARWLS-AEKF的锂电池SOC估计[J].电子测量技术,2022,45(17):43-50.

[8] 邢丽坤,詹明睿,郭敏,等.基于FFMILS-MIUKF算法的锂电池SOC估计[J].电子测量技术,2022,45(16): 53-60.

[9] 宋旬.电动汽车串并联动力电池组建模与性能分析研究[D].西安:长安大学,2019.

[10] 程燕兵,韩如成.锂电池PNGV模型与二阶RC模型分析与比较[J].太原科技大学学报,2019,40(6):430- 436.

[11] 刘征宇,朱诚诚,尤勇,等.面向SOC估计的计及温度和循环次数的锂离子电池组合模型[J].仪器仪表学报,2019,40(11):117-127.

[12] 孙鹏宇,李建良,陶知非,等.动态工况电池在线参数辨识及SOC估计研究[J].电子测量与仪器学报,2021, 35(1):10-17.

[13] CHEN X, LEI H, XIONG R, et al. A Novel Approach to Reconstruct Open Circuit Voltage for State of Charge Estimation of Lithiumion Batteries in Electric Vehicles[J]. Applied Energy,2019,255:113758.

[14] 安诺静.基于EKF的电动汽车用锂离子电池SOC估计方法研究[D].西安:长安大学,2020.

SOC Estimation of Lithium Battery Based on ARWLS and AUKF

ZHOU Qin1, SHEN Hui1, SUN Mingzhu2, CHEN Zhengrong1, XU Pengcheng1

( 1.Yangzhou University, Yangzhou 213000, China;2.School of Automotive Engineering, Hefei Vocational and Technical College, Hefei 238010, China )

Precise estimation of lithium battery state of charge(SOC) has a profound impact on the safe and stable driving of pure electric vehicles. The estimation of lithium battery SOC state mainly includes two hot issues: parameter identification algorithm and SOC estimation algorithm. Aiming at the "data saturation" phenomenon in the identification process and the filtering divergence problem in lithium battery SOC state estimation, this paper proposes a joint algorithm of adaptive forgetting factor recursive least squares (ARWLS) and adaptive unscented kalman filter (AUKF). First, the mathematical model of the second order R-C lithium battery is established. Aiming at the "data saturation" phenomenon in the parameter identification process of the traditional least squares method, an adaptive forgetting factor is introduced to dynamically modify the weight of the new and old data, so as to improve the accuracy and efficiency of online parameter identification. Secondly, aiming at the filtering failure problem of unscented kalman filter, an adaptive unscented kalman filter algorithm is proposed to adaptively system noise and observation noise, so as to improve the adaptability and robustness of SOC estimation. Finally, three SOC estimation algorithms, extended kalman filter(EKF), unscented kalman filter(UKF) and AUKF, are simulated and compared under hybrid pulse power characterization(HPPC) working condition. The simulation results show that the SOC curve estimated by AUKF algorithm has the best performance following the change of the true value curve of SOC, and the estimation accuracy is also better than the other two algorithms, with smaller estimation error and the best convergence.

Lithium battery; State of charge; On line parameter identification; ARWLS; AUKF

10.16638/j.cnki.1671-7988.2023.03.002

TM912

A

1671-7988(2023)03-05-10

周琴（1997—），女，硕士研究生，研究方向为新能源汽车控制技术，E-mail:1224934390@qq.com。

扬州大学大学生科技创新基金（X20210328）。