基于土壤水热耦合运移基础理论构建水文地质数学规律模型
程克俊
(安徽省六安水文水资源局,安徽 六安 237000)
大自然中水资源的存在形式有地表水、地下水、大气中的水分子、土壤水、植物水等,并且多种形式的水会相互转化,多种水资源之间的转化和运移的纽带是土壤中的水分子,转化运移形式一般为蒸发、降水、灌溉和植物中水分子的交换等。在运移和交换的过程中,热量的传输是与土壤水的运移相联系的,土壤中水和热的运移相互作用,水的分布和变化会使土壤的热特性参数发生改变,从而使其温度改变,进而使土壤中水的各项性质以及各项运动参数发生改变,从而使土壤水发生运移。
本文基于土壤水热耦合运移基础理论,以皖西丘陵地区区域代表站为例,构建水文地质数学规律模型并进行参数反演,旨在促进土壤水的变化规律及其他相关问题的研究。
1 皖西丘陵地区水文地质现状
皖西丘陵地区位于安徽省江淮西部,指大别山区及其附近的丘陵,按照地貌类型的不同,分为北、中、南次级单元。该区年平均气温低于15℃,由于地势原因,该区热量资源较低、雨水较多,海拔400~500m为黄棕壤土,500m以上为棕壤土和草甸土。
通过望城岗实验站和姚李实验站的监测数据可看出,降水量在2019—2020年发生突增,同时土壤蒸发量和水面蒸发量降低,见表1。

表1 望城岗实验站和姚李试验站年平均降水量与水面、土壤蒸发量变化
由于水的形式是不断变化的,土壤中的水分存在量及形式和其热量也是相互影响的,土壤中的热量其数值及差异导致土壤中的水分发生迁移及变化。皖西丘陵地区内部水汽不易扩散,随着降雨量的增加,周边温度降低,使水面蒸发量和土壤蒸发量随之降低。但业内并没有成熟的数学模型和规律来表示降水量的增加和蒸发量的降低之间的必然联系,通过研究水热耦合运移理论,可以相对科学地研究蒸发量和降水量之间的相对关系。
2 土壤水热耦合运移基础理论概述
随着对土壤水动力学理论的深入研究,通常将传统的日常观测和实验研究相结合,通过确定土壤水热参数和空气动力学参数,构建数学规律模型对土壤与大气之间的水热运移进行模拟,从而得到土壤水地表或潜水蒸发计算方法。模型是在试验数据的基础上进行数值计算的,可靠性较高,能够填补因观测时段间隔而没有观测数据的空白,对于水热运移模拟问题的深入研究有很大帮助。如今对于土壤表面蒸发不受土壤水分胁迫的模拟研究较多,但是对于长时间的土壤与大气间的水热运移模拟还比较少。
土壤的表面受到阳光和其他方式的辐射,与大气层进行水汽和湿热交换,并且与土壤的深层部分进行热量交换,土壤下表面与潜水层进行水分和热量交换。建立土壤水热耦合运移数学规律模型,对土壤和大气之间的水热平衡进行模拟并进行分时段求解,能够得到土壤的蒸发量、水热状况和地表能量平衡等变化规律。
3 水文地质数学规律模型
3.1 水文地质数学规律模型构建
土壤水热耦合运移由水流和热流两部分组成,因此数学规律模型也是由这两部分基本方程组成。
a.水流基本方程为
S(z,t)
(1)
式中:h为负压水头,cm;t为时间,s;z为土壤深度,cm;C(h)为比水容,L/min;K(h)为导水率,cm/min;S(z,t)为根系吸水速率,cm3/min;T为温度,℃。
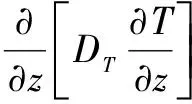
b.热流基本方程为
(2)
式中:CV为容积热容量,J/m3·K;Kc为导热率,J/(m2·s·k);t为时间,s;z为土壤深度,cm。
c.水文地质数学规律模型,根据能量守恒定律和连续性方程可表示如下:
(3)
3.2 水文地质数学规律模型求解
3.2.1 基本方程定解和选取差分方程剖面节点
a.水流基本方程的定解条件。
初始条件:
h(z,t)|t=0=h0(z)
(4)
上边界条件:
(5)
下边界条件:
h(z,t)|z=H=hH
(6)
b.热流基本方程的定解条件。
初始条件:
t(z,t)|t=0=t0(z)
(7)
上边界条件:
(8)
下边界条件:
T(z,t)|z=H=TH
(9)
c.在z-t坐标系中,z轴由大小均等的m个单元组成,节点数量为m+1,间距为Δz,编号i=0,1,2,…,m;t轴由大小均等的n个单元组成,节点数量为n+1,间距为Δt,编号k=0,1,2,…,n。
3.2.2 土壤水热耦合运移方程的差分离散
使用隐式差分格式得到水热流方程的差分离散为
(10)
3.2.3 边界条件的差分离散
a.水流基本方程边界条件离散。
初始条件:
(11)
上边界条件:
(12)
整理得
(13)

下边界条件:
(14)
b.热流基本方程边界条件离散。
初始条件:
(15)
上边界条件:
(16)
进行整理:
(17)
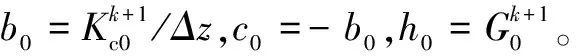
下边界条件:
(18)
c.节点之间各水热参数的确定。
(19)
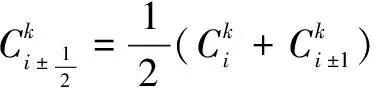
(20)

(21)

(22)
3.2.4 差分方程整理
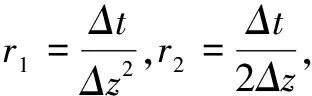
(23)
i为0时,上边界条件为
(24)
i为m时,应用下边界条件式(14)可写成
(25)
(26)
列三对角代数方程组:
(27)
b.热流差分方程整理。
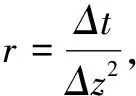
(28)
i为0时,上边界条件为
(29)
i为m-1时,应用下边界条件式可写成:
(30)
(31)
列三对角代数方程组:
(32)
3.3 方程组求解

(33)
式中:p为进行迭代的次数;e为相对误差的允许值,取0.001。
在计算时,空间步长选用2cm,时间步长选用1h。
(34)
式中:p为进行迭代的次数;e为相对误差的允许值,取0.001。
4 水文地质数学规律模型参数反演
4.1 水分运移模拟
以2020年9月21日0时作为模型初始值,收集3天内的土壤含水率数据,以望城岗站的土壤监测数据为例,9月21日0时至23日24时,望城岗站每日降水量分别为0、1.0mm、0.5mm,土壤蒸发量分别为1.0mm、1.2mm、0.9mm,模拟其土壤含水率的变化,并和实测数据进行比较,见图1。由图1可知,模拟值和实测数据基本吻合。
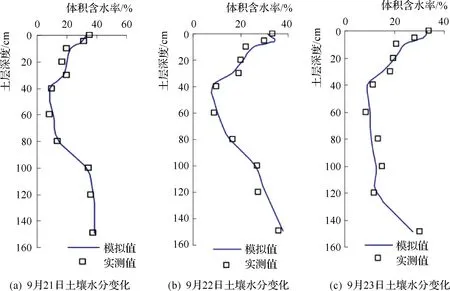
图1 皖西丘陵地区土壤含水率实测值和模拟值比较
4.2 热量运移模拟
图2为皖西丘陵地区望城岗站4种不同深度下的土壤,在2020年9月21—23日连续72h内,其温度的模拟值和实测值,通过比较,模拟值和实测值基本吻合。在距离表面5cm的深度,土壤温度由于受到阳光辐射,每天的变化具有周期性,土壤表面的温度每天变化的幅度最大,对其模拟的情况与实际测量的结果基本相符。土壤深度越向下,其温度每天的变化越不明显,在土壤深度到达80cm时,土壤温度基本上没有变化,可以认为在80cm深度以下,土壤温度在一天中基本不变,只是随着季节的改变,每天温度随之发生改变。

图2 皖西丘陵地区不同深度土壤温度实测值和模拟值的比较
4.3 模型检验
本文使用土壤水热耦合数学规律模型,对皖西丘陵地区土壤的水热运移规律进行数值模拟,其土壤中含水率模拟和实测数值间的偏差见表2。
从表2可以看出,皖西丘陵地区土壤水分变化的模拟预测精度比较高,土壤在不同深度,其含水率的模拟值和实测值之间比较一致,最大偏差为0.117,最小偏差为0.022,平均偏差为0.077,结果比较令人满意。

表2 皖西丘陵地区9月23日土壤含水率模拟和实测数值间的偏差
5 结 语
根据土壤含水量和土壤温度的模拟结果,可以得出:在简化植被、温度变化、风量等条件下,测算的土壤含水率和实测值相对一致。同时,土壤温度也可以进行相应模拟计算。本文使用的土壤水热耦合水文地质数学规律模型能够基本反映皖西丘陵地区的土壤水热运移过程,在研究皖西丘陵地区的生态结构时使用该计算模型,在水热资源互换及优化过程中利于水资源可持续应用,对水资源可持续发展具有可借鉴意义。

