基于图表示深度学习的异质网络链路预测研究
赵宇红,吴 昊
(内蒙古科技大学 信息工程学院,内蒙古 包头 014010)
1 引 言
在现实世界中,网络[1]可以很好地描述每个实体以及每个实体之间的关系,其中实体对应网络中的节点,边则表示两个实体之间的关系.现实生活的网络一般都是复杂网络,结构复杂且数据丰富,从中挖掘和分析得到有价值的信息引发了学者的广泛关注.链路预测[2]是网络研究的中比较有挑战的一个任务,它主要是对网络中的丢失信息或者潜藏信息进行预测,从中挖掘出更有价值的信息为现实世界所应用.
链路预测是一种应用于复杂网络的结构化分析技术,它的目标主要是通过对网络结构以及节点之间的相互关系进行分析,从而预测节点之间是否存在连接的可能性,由此应用到如今的生活当中.例如,当今社交媒体软件的好友推荐[3],根据用户的喜好和行为,推荐用户相同爱好的好友;在电子商务[4]中,根据对用户的行为和购买喜好进行分析,筛选最符合用户的商品进行推荐,实现商品的推广,促进消费.
随着计算机技术的发展,深度学习走入人们的视野,并在自然语言处理,图像处理等方面取得了巨大的突破,链路预测从中获得一定的启发,深度学习也开始成为链路预测的一大研究热点.其中图表示学习[5]可以将图数据转化成低维稠密的向量化表示,同时确保图数据的某些性质在向量空间中也能够得到对应,并且图数据的表示可以包含丰富的语义信息,可以为链路预测提供更为优秀的输入特征.
现今国内针对大多数链路预测的研究都是针对单一网络或者同质网络,但是随着异质网络[6]的发展,异质网络中包含的节点和链接更加综合全面,使得异质网络的链路预测成为了一个重要研究方向.
根据上面的论述,本文提出了一种图表示学习下的异质网络链路预测,本法的方法大致如下:
1)根据异质信息网络构建一个多通道网络[7],其中每一个通道表示一种元路径下的子网络,每个子网络都是同质网络,每一个路径代表着不同的语义信息,然后可以对每一个通道进行图卷积操作.
2)传统的GCN(Graph Convolutional Network)[8]只能学习浅层的网络,为了学习深层次的关系特征,于是本文使用了GraphInception模型[9],该模型改进了传统的inception模型,使其可以处理图数据.GraphInception模型由不同规格的卷积核组成,并且通过多层堆叠,构造了从简单到复杂的关系特征的层次结构.由此,本文可以使用该方法,对上文的多通道网络进行深层次的关系特征提取,得到更加全面准确的关系特征向量.
3)通过计算Hadamard距离处理关系特征向量来表示边向量,并通过训练逻辑回归函数来评估边存在的概率,最终完成链路预测任务.
2 相关知识介绍
2.1 图表示学习
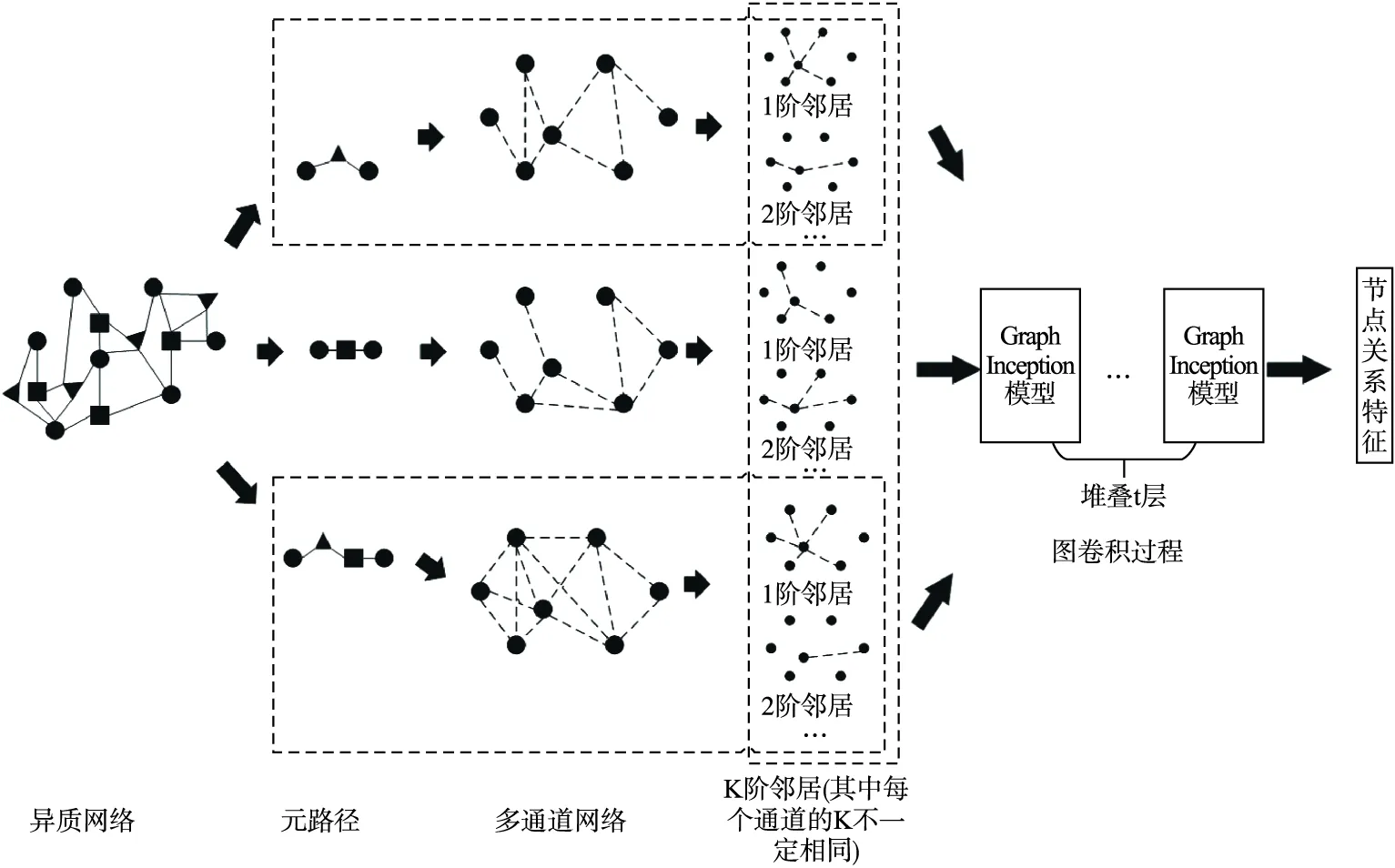
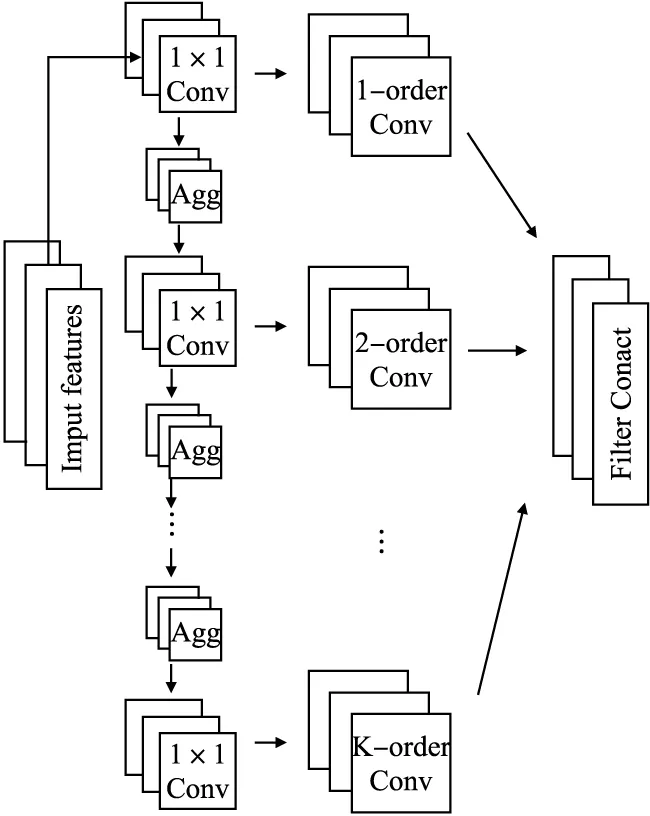
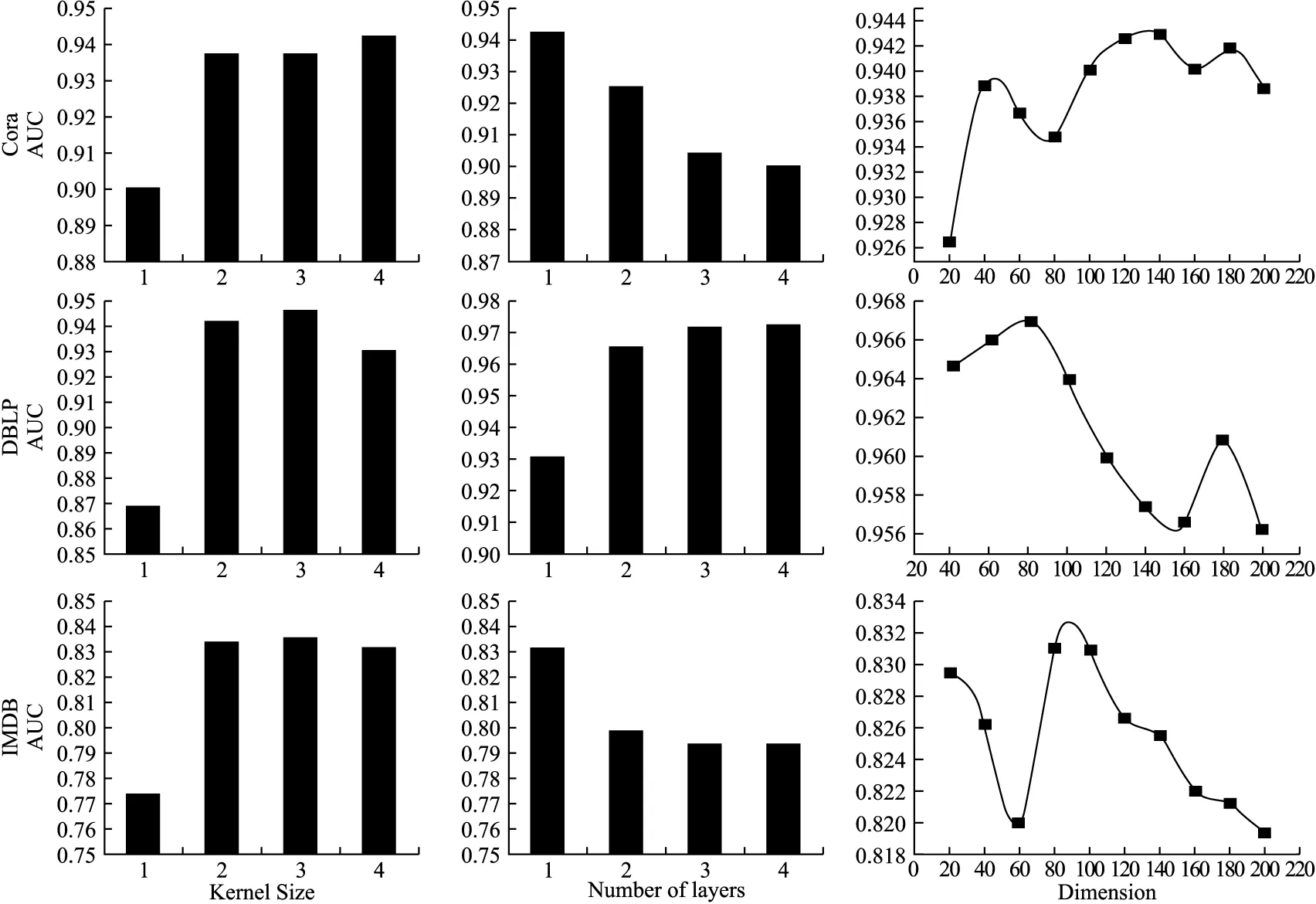
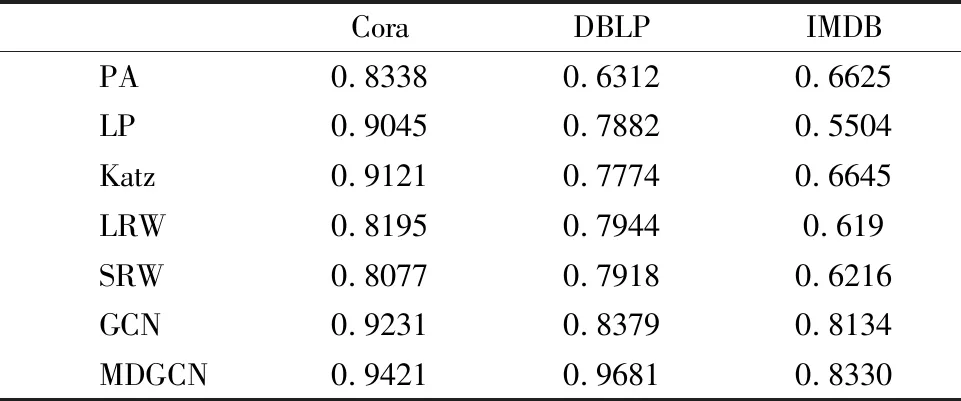
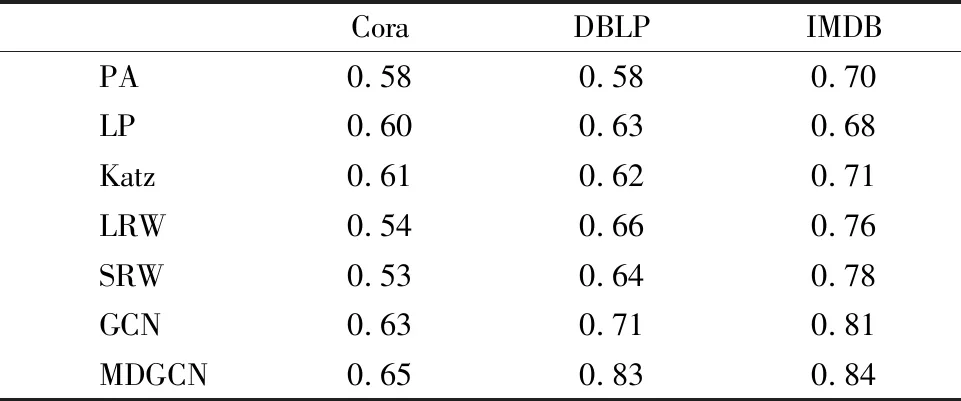
网络表示学习的主要目标是学习网络顶点的潜在低维表示,同时保留网络拓扑结构、顶点内容和其他辅助信息,在学习新的顶点表示之后,通过将传统的基于向量的机器学习算法应用到新的表示空间,可以容易且有效地执行网络分析任务.其在节点分类[10],链路预测等任务中取得了不错的进展.网络可通过图进行建模,但通常都是高维的,难以处理,图嵌入可以作为一种降维的技术,通过构造一个D维的空间,将图的节点嵌入到d(d< 本文使用的就是第3种方法,通过一种高效的图卷积网络(GCN)学习网络节点的向量表示,然后将向量表示应用于链路预测中. 传统的链路预测的度量方法大部分是使用基于相似性的方法,这些方法通过使用图的结构属性在节点对(vx,vy)之间度量相似性分数S(vx,vy)来评估产生链接的可能性,主要有如下方法: 2.2.1 基于局部信息的相似性指标 PA(Preferential Attachment)指标[11]只考虑到节点度数的影响,如果两个节点度数越高,则两个节点之间的相似度越大.在某些特定的网络中能取得很好的预测效果.如在路由网络中,PA 指标的预测效果都明显高于其他指标,其计算公式如公式(1)所示: S(vx,vy)=kxky (1) 其中,kx表示节点vx的度数. 2.2.2 基于路径的相似性指标 1)LP(Local Path)局部路径指标[12],该指标是对于CN(共同邻居)指标的改进,主要体现在其考虑到节点的2阶,3阶邻居的贡献.由于2阶邻居更为重要,该指标使用了可调参数α控制3阶路径,其定义如公式(2)所示: (2) 2)Katz指标[13]考虑的是两节点之间全部路径,由于短路径需要更多的权重,于是Katz指标使用了权重衰减因子β,当β十分小的时候Katz指标就和CN指标表现得差不多.其定义如公式(3)所示: S=βA+βA2+βA3+… (3) 2.2.3 基于随机游走的相似性指标 1)LRW(Local Random Walk)局部随机游走指标[14],该指标为了减少了计算复杂度,使用了限制随机游走过程中步长大小的方法,其适用于规模较大、节点稀疏的网络.其定义如公式(4)所示: (4) 其中pvi,vj(t)表示从节点vi出发经过t步之后到达节点vj的概率,E表示网络节点的连边集合,k表示节点的度. 2)SRW(Super-posed Random Walk)叠加随机游走指标[14],它在LRW的基础上考虑了目标节点与其相邻节点连边的可能性,在随机游走过程中将游走者每一步的概率都计算进去从而得到叠加的局部随机游走指标.其定义如公式(5)所示: (5) 异质信息网络是信息网络的一种,它包含了更丰富的语义信息(节点或边具有多种类型).可以将其定义为G=(V,E),其中V代表着节点的集合,E代表节点之间边的集合,同时存在一个节点类型的映射函数φ:V→A和一个变类型映射函数Ψ:E→R,并且要求节点类型|A|>1或者边类型|R|>1. 本文提出的MDGCN(Multichannel Deep Graph Convolutional Network)模型主要是通过将异质信息网络进行多通道划分,接着对于每个通道进行图卷积操作,最终获得节点的关系特征用于下游任务:链路预测.图卷积过程使用graph inception模型,从而能够进行深层次的关系特征获取,解决传统GCN只能学习浅层网络的问题.该算法框架如图1所示. 图1 MDGCN模型的过程Fig.1 Process of MDGCN model 异质网络拥有丰富的节点类型,而不同的节点类型之间也存在着差异,因此网络上的卷积运算变得难以解决.元路径是异质网络中节点关联的路径,能丰富的表达一类节点中节点之间的语义信息,不同元路径表达了不同的含义和不同的链接网络.于是本文使用了多通道网络,以元路径对异质网络进行划分,划分之后的每一个通道都是由目标类型节点组成的同质网络,代表着不同语义,从而可以获得节点不同语义下的链接关系. 本文首先通过在有限长度内用广度优先算法获取异质网络中由目标类型节点组成的元路径(每条元路径代表着节点之间的唯一关系),从而得到多个同质网络作为多通道网络的输入. 元路径定义如式(6)所示: S={P1,…,Pn} (6) 其中,n表示元路径的数目. 从而可以将多通道网络定义为: (7) 其中V1代表目标类型节点集合,e1l代表V1之间的关系(即V1之间一种类型关系边的集合),它们通过元路径Pl连接. 3.4.1 图卷积的介绍 传统的图卷积模型只适用于同质网络,本文将其扩展到异质网络,从而可以通过非目标类型节点来细化目标类型节点的关系特征.同质网络Ghomo上的卷积可以定义为特征向量X与对称归一化邻接矩阵P(转移概率矩阵)上的滤波器gθ的乘积,如式(8)所示: gθ⊗GhomoX=gθ(PX)=gθ(U∧UT)X=Ugθ(∧)UTX (8) 为了选择给定节点的局部邻居,本文将gθ定义为多项式参数滤波器: (9) 其中参数θ是多项式系数的向量. 所以最终可以得出同质网络Ghomo上的卷积公式: (10) 这个表达式表示的是K阶邻域,因为它是转移概率矩阵的第K阶多项式. (11) (12) 其中,Θlk=(1=1,…,n)为滤波器参数矩阵,向量x的函数r定义为r(x)=(r(x1),…,r(xm)),函数中r(xi)=max(0,xi)是Relu函数,H的第i行向量表示节点v1i学习的关系特征. 与传统的图卷积模型相比,本文的模型学习的是关系特征,而不是内容特征,因此本文的模型不需要考虑节点本身的属性,即K=0的情况.并且,本文的模型可以应用于异质网络,而传统的图卷积模型不能. 3.4.2 深层次的图卷积方法 一个异质网络通常涉及一个多关系层次结构,然而,公式(12)只捕获每个子网中的潜在关系.也就是说,它既不处理不同类型节点之间的复杂交互,也不捕捉不同子网中潜在关系之间的不兼容性.在图1中,受zhang等人工作[9]的启发,本文设计了一种基于Graph Inception模型的关系特征学习方法,以通过多层卷积从现有的多关系层次生成深层关系特征. 传统的Inception模型只能处理欧几里得数据,不能够运用在一般的图结构中,例如:网络数据,因此为了更有效得学习网络中的关系特征,本文使用了Graph Inception模型,该模型框架如图2所示. 图2 Graph Inception模型框架图Fig.2 Graph Inception model frame diagram 如图2所示,Graph Inception结合不同大小的卷积核提取关系特征,以通过多层卷积从现有的多关系层次生成深层关系特征.其中,本文为每一层上的每个子网取两个卷积核,并将核大小分别设置为1和2,则Graph Inception模型的第t层的定义如式(13)所示: (13) (14) 于是通过计算可以得到最终目标类型节点的关系特征如式(15)所示: (15) 接着,通过堆叠多个Graph Inception层来提取复杂的关系特征,并通过调整层数来控制学习到的关系特征的复杂性. 与公式(12)相比Graph Inception模型拥有3大优点: 2)当网络很深的时候该方法所需要的参数更少. 3)该模型能够缓解具有非常宽的节点度分布的图的局部邻域结构上的过拟合问题. 在学习了所有目标类型节点的关系特征之后,本文通过随机选取目标类型节点V1中的任意两个节点V1i和V1j,然后经过计算Hadamard距离来表示边向量,并通过训练逻辑回归函数来评估边存在概率.边向量的定义如式(16)所示: eij=Hi⊙Hj (16) (17) 得到两节点之间连接的概率之后,本文可以通过逻辑回归函数计算其损失,如公式(18)所示: (18) 其中,yij表示在元路径S下V1i和V1j是否链接,若连接yij=1,否则yij=0;N表示目标类型节点V1中两节点之间可能存在边的数目. 本文选取了3个拥有着不同节点类型数目的数据集,通过MDGCN模型构造多通道网络分解异质网络,使用GCN进行学习和训练,从而获取目标类型节点的关系特征向量,最终通过逻辑回归完成链路预测.同时,为了验证本文方法的可行性,本文选取了一些传统的链路预测方法:PA,LP,Katz,LRW,SRW进行了对比实验分析. 为了验证本文模型的有效性,本文选取了3个真实的数据集进行了实验: ·Cora数据集[15]:该数据集是一种典型的论文引用网络,它具有2种类型的节点,即论文和作者,以及两种类型的链接:作者和作者链接,作者和论文链接.在实验中本文将论文视为目标类型节点,论文标题的独热向量作为每个论文的内容特征. ·DBLP数据集[16]:该数据集是一种书目信息网络,它具有3种类型的节点,即会议,论文和作者,以及两种类型的链接:作者和论文的链接,论文和会议的链接.在实验中本文将作者作为目标类型节点,作者发表的论文标题的独热向量作为目标类型节点的内容特征. ·IMDB数据集[17]:该数据集是一个电影数据集,其包含了4种类型的节点,即电影,导演,演员和女演员,其中有3种类型的链接:电影与导演的链接.电影与演员的链接,电影和女演员的链接.在实验中本文将电影作为目标类型节点,一个关于电影的所有情节摘要的独热向量作为目标类型节点的内容特征. 3个数据集参数如表1所示. 表1 数据集参数Table 1 Data set parameter AUC指标[18]作为链路预测中的常用方法,它能够从整体上衡量链路预测结果的准确性,在衡量一个算法好坏的时候,本文需要将数据集划分为训练集和测试集,则AUC可以被解释为从测试集中随机抽取一条链接的预测值比随机从不存在链接中选择的一条链接的概率值大的可能性.也就是说,AUC是将从测试集中选取的链接的分数与随机从不存在链接中选择的链接的分数相比较,当前者分数大于后者则加1分,两者相等加0.5分,否则不加分.之后进行独立随机比较n次,记加1分的次数为n′,加0.5分的次数为n″次,则AUC的计算公式定义为: (19) 由此可见,如果所有分数都是随机产生的AUC=0.5,所以AUC比0.5大得越多算法越精确. Precision指标[19]相比于AUC从宏观的角度评价算法的准确性,它只考虑了前L位是否预测准确,也就是将不存在的边根据所对应的概率值进行排序,排序后选择前L个(本文的L=100)与测试集进行比对,得出Precision的公式: (20) 其中N表示L中属于测试集的数目. 本文将实验数据随机划分为训练集和测试集,划分比例采取9:1的比例,之后进行100次独立实验,对于每次独立实验都要求其 AUC值和Precision值,最终将所得到的所有AUC值和Precision值进行平均值计算作为最终的实验结果.其中对于每一次独立实验都要进行10000次的随机抽样比较预测边与不存在边的分数计算AUC和Precision. 4.3.1 参数分析 本节分析MDGCN模型中的参数,包括:图卷积过程中卷积核的大小k,节点向量表示的向量维度d和Graph Inception模型堆叠的层数t.其中卷积核的大小影响着感受野(receptive field),一般情况下,随着卷积核大小的增加,感受野会随之变大,看到的网络信息就会越多,所获得的全局特征越好.虽说如此,但是更大的卷积核会影响到计算复杂度,导致模型深度增加的计算难度提升,计算性能严重下降;节点向量表示的维度则用来刻画节点向量映射空间的复杂程度;层数t的数量影响着深层次节点关系特征的获取程度.在Cora,DBLP,IMDB 3个数据集下各个参数对AUC的影响,如图3所示. 图3 MDGCN模型的参数分析Fig.3 Parameter analysis of MDGCN model 本文使用了控制变量法对3个数据集中的节点向量维度、卷积核大小以及堆叠层数对预测结果AUC的影响进行了测试.其中,默认kernel size=4,number of layers=1,Dimension=100,对于卷积核大小与堆叠的层数的调节步长都设置为1,节点向量维度则以20为调节步长. 从图3中可以看出,在控制其他参数大小不变的情况下,随着卷积核的大小不断变大,AUC都呈增加趋势,在DBLP和IMDB中卷积核大小在3的时候得到了最优表现,Cora数据集中虽然还在增长,但是不是很明显,为了减少计算复杂度选取大小4左右的卷积核就行.对于关系更加复杂的DBLP中堆叠层数的大小对AUC的影响也足够明显,但在关系相对简单的Cora和IMDB中的效果不是很好.对于节点向量维度,不同维度对于AUC的影响波动大小无明显差异,波动的范围大概在0.03左右,整体效果都不错.其中,Cora数据集在120~140之间,DBLP数据集在60~80之间,IMDB数据集在80~100之间达到最优效果. 4.3.2 实验结果 本文使用PA,LP,Katz,LRW,SRW 5种指标作为校准方法与本文方法进行对比,它们的对比结果如表2和表3所示. 表2 各方法在不同数据集下的AUC值Table 2 AUC values for each method in different data sets 表3 各方法在不同数据集下的Precision值Table 3 Precision for each method in different data sets 通过表2可知,对于节点类型和边类型都较少的论文引用网络Cora来说,各种方法的效果都不错,LP、Katz、GCN都达到了0.9以上,PA,LRW,SRW也都达到了0.8以上.由于Cora中节点数目较多,但连边数却相对较少,所以考虑节点度的PA算法效果不是很理想.由于Cora网络规模不是很大,Katz指标取得了传统算法中的最优结果,本文的方法比其还拥有了3%的提升,由此可见本文方法有着更高的准确率. 对于连边类型数目与Cora相同,节点类型更多的书目信息网络DBLP,传统算法的AUC都有所下降.只考虑节点度的PA算法对网络链路的预测只能得到0.6312,效果明显欠佳.考虑高阶节点信息的LP算法一定程度增加了网络的局部连通性,准确度有所提升.考虑全局路径的Katz算法,相比于LP准确度也有所提高.基于随机游走的LRW,SRW方法更加适合该数据集,相比于其他传统算法,这两种算法的准确度更高.相较于这些算法基于图表示学习的GCN和MDGCN能同时考虑网络的复杂结构和多样化的属性类型,使得准确度得到了一定的提升.其中MDGCN考虑了深层次的节点关系,相较于GCN还提高了13.02%. 在节点类型和连边类型都比较多的IMDB网络中,传统的算法PA,LP,Katz,LRW,SRW方法表现都十分欠佳,AUC处于0.7以下.本文提出的方法能够取得较好的预测结果,相比较于效果最好的传统图表示学习算法GCN有了1.96%的提高,对于传统算法有了百分之十以上的提高.对于同样使用图表示学习的GCN算法,MDGCN通过多通道网络考虑了网络的异质性和不同类型边的语义信息,并在卷积过程中考虑了更深层次节点的关系,从而得出了更具有表现的节点关系特征向量,利用该向量得出的边向量进行逻辑回归,从而得出了更加精确的结果. AUC值虽然是链路预测中最为重要的指标,但是当AUC之间相差不多的时候,Precision值有着关键的作用.在AUC值相差无几的时候,Precision值越高,代表算法的准确性越好.可以通过表3得知,本文的方法在3个数据集的表现依旧有较好的提升. 综上所述,本文提出的MDGCN方法在不同节点类型数目和不同连边类型数目的网络中都可以表现出相对较好的预测精度. 本文研究了一种在异质网络中进行链路预测的方法,即MDGCN模型,该方法提出一种使用多通道网络分解异质网络,用Graph Inception模型获取节点关系特征,最终通过逻辑回归进行链路预测.此方法能够高效处理图数据,使图数据的某些性质在向量空间体现,从而得到丰富的节点信息和语义信息,让向量能够更加准确得表示节点.通过实验结果可以得出,MDGCN模型对Cora,DBLP和IMDB真实数据集均表现出良好的预测结果. 本文提出的方法是基于当前状态进行预测,没有考虑到时间因素对网络的影响(即网络的拓扑结构可能随时间变化而发生改变).同时,对于关系层次相对简单的网络,本文方法通过堆叠层数效果反而不是很理想,需要进一步得改进.所以,后续的研究将会着手于考虑通过时序网络模型的引入,研究动态网络下的链路预测方法.2.2 相关指标介绍
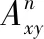
3 MDGCN模型
3.1 异质信息网络的定义
3.2 MDGCN模型的基本思想
3.3 构造多通道网络
3.4 MDGCN算法
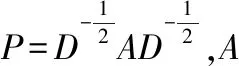
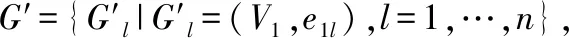
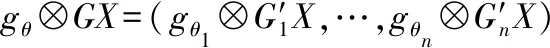
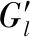
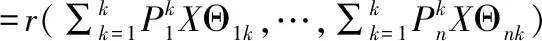
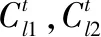
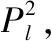
3.5 训练模型
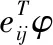
4 实验及结果分析
4.1 数据集

4.2 评价指标
4.3 实验结果与分析
5 总 结

