Exploiting the Direct Link in IRS Assisted NOMA Networks with Hardware Impairments
Ziwei Liu,Xinwei Yue,*,Shuo Chen,Xuliang Liu,Yafei Wang and Wanwei Tang
1Key Laboratory of Modern Measurement&Control Technology,Ministry of Education,School of Information and Communication Engineering,Beijing Information Science and Technology University,Beijing,100101,China
2The Party Committee Office,Yellow River Conservancy Technical Institute,Kaifeng,475001,China
3Tangshan University,Tangshan,063000,China
ABSTRACT Hardware impairments(HI)are always present in low-cost wireless devices.This paper investigates the outage behaviors of intelligent reflecting surface (IRS) assisted non-orthogonal multiple access (NOMA) networks by taking into account the impact of HI. Specifically, we derive the approximate and asymptotic expressions of the outage probability for theIRS-NOMA-HI networks. Based on the asymptotic results, the diversity orders under perfect self-interferencecancellation and imperfect self-interference cancellation scenarios are obtained to evaluate the performance of the considered network. In addition, the system throughput of IRS-NOMA-HI is discussed in delay-limited mode. The obtained results are provided to verify the accuracy of the theoretical analyses and reveal that:1)The outage performance and system throughput for IRS-NOMA-HI outperforms that of the IRS-assisted orthogonalmultiple access-HI(IRS-OMA-HI)networks;2)The number of IRS elements,the pass loss factors,the Rician factors,and the value of HI are pivotal to enhancing the performance of IRS-NOMAHI networks;and 3)It is recommended that effective methods of reducing HI should be used to ensure system performance,in addition to self-interference cancellation techniques.
KEYWORDS Hardware impairments; imperfect SIC; intelligent reflecting surface; non-orthogonal multiple access; outage probability
1 Introduction
As a promising technology to achieve significant improvement in system throughput and energy efficiency, non-orthogonal multiple access (NOMA) has recently attracted growing attention for the sixth-generation (6G) communication networks [1,2]. Different from the traditional orthogonal multiple access (OMA), the main advantage of NOMA technology is that it allows multiple users to utilize the same resource and realize the correct demodulation by introducing the successive interference cancellation (SIC) technology, which can improve the utilization of spectrum resources [3]. It has been demonstrated that power domain NOMA can ensure much higher throughput in underlay cognitive radio networks than conventional OMA [4]. NOMA also can contribute significantly to improving the quality of service, which provides a balanced service comparatively for serving multiple devices [5,6]. In order to enhance the system’s performance, the integration of NOMA and cooperative communication has been proposed in [7,8]. In particular, the authors of [9] concluded that the outage behaviors and ergodic rate of cooperative NOMA systems are better compared to traditional cooperative communication. To achieve enhanced spectrum efficiency, the authors of [10,11] analyzed the outage performance of users for amplify-and-forward and decode-and-forward relays in cooperative NOMA systems.
Meanwhile, intelligent reflecting surface (IRS) is deemed as another new transmission technology for future wireless networks [12-14], which consists of numerous precisely designed arrangements of electromagnetic units, and the signal is controlled by changing the phase and amplitude of the incident wave [15]. There are some advantages of IRS:i) IRS can enrich the channel scattering conditions, enhance the system’s multiplexing gain, and improve the received signal strength [16];ii) The lightweight and low power requirements of the IRS make it easy to deploy on various scattering surfaces in wireless propagation environment, such as buildings,roadside billboards, windows, and interior walls [17]; andiii) Unlike the traditional active relay,IRS reflects signals in full-duplex mode through passive beamforming and does not impose additional energy consumption and noise [18]. These features have attracted researchers to apply it to various new wireless communication scenarios. Specifically, the authors of [19] showed that IRS deployment could effectively improve wireless networks’throughput, energy efficiency and coverage performance. In [20], the IRS-assisted wireless communications were introduced in an end-toend transmission scenario, which demonstrated that deploying an IRS structure can substantially improve the pairwise error probability metric. The aforementioned works manifest that IRS yields significant performance in communication scenarios.
Inspired by the appealing advantages of IRS and NOMA, some recent works have investigated the interplay between IRS and NOMA, which can achieve enhanced massive connectivity with higher network spectral efficiency and user fairness [21-23]. The authors of [24] demonstrated that combining IRS and NOMA is an effective strategy to enhance communication coverage and energy efficiency. Furthermore, the authors of [25] proved that IRS-NOMA could achieve superior performance compared to the counterpart IRS-OMA schemes. With the help of a 1-bit coding scheme, the outage probability and ergodic rate for IRS-NOMA networks under Rayleigh fading channels have been analyzed considering the impact of perfect SIC (pSIC) and imperfect SIC(ipSIC) scenarios [26]. Moreover, in [27], the authors assessed the impact of IRS phase-shifting design on the outage probability through two-phase configurations, i.e., a random phase and coherent phase shifting. The authors of [28] minimized the transmit power of the IRS-NOMA system by optimizing the beamforming vector at base station (BS) and the phase shifters at IRS. As a further development, the interplay between IRS and NOMA is widely investigated for various technologies like unmanned aerial vehicle [29], deep reinforcement learning [30], mobile edge computing [31] and physical layer security [32]. The previous works were applied to the ideal hardware conditions.
However, it is challenging to achieve the perfect performance in practice with the existence of hardware impairments (HI), and residual interference [33,34]. Specifically, HI causes errors in the transmitted signal at the transmitter and reduces the detection quality of the received signal at the receiver [35]. Under the realistic assumptions of residual HI, channel estimation errors and ipSIC,the authors of [36] investigated the NOMA systems with an emphasis on reliability and security. In[37], the performance of full-duplex NOMA networks over Rician fading channels was described and shown the influence of ipSIC on the system is more pronounced than that of HI. The authors employed multiple relays with finite energy storage capability to assist the BS to two NOMA device users’transmission transmission of the NOMA network in [38], and the outage probability expressions of users were derived to evaluate the system performance. Considering the IRS-assisted wireless communications, the existence of HI will affect both the source transmit beamforming and the IRS reflecting beamforming designs [39]. To compensate for the losses caused by HI,various analog and digital signal processing schemes are discussed in [40]. Despite these efforts,the HI still degrades the performance of wireless communication networks. As a further advance,the authors of [41,42] analyzed the system performance under the impact of HI at both BS and users on various NOMA and multiple input multiple output (MIMO) networks.
1.1 Motivations and Contributions
Motivated by the aforementioned observations, we study the performance of an IRS-NOMA network by incorporating signal distortions caused by HI. Until now, most of the existing research contributions for IRS-NOMA with ipSIC/pSIC over Rician fading channels have considered the optimization questions. Motivated by the observations mentioned earlier [43,44], we considered an IRS-NOMA communication system over Rician channels by incorporating signal distortions caused by HI in the transmitter and receiver. In contrast to the literature [26], we extend our analytical results from the Rayleigh channels to the more general Rician fading channels. Compared to [24], the direct communication link from the BS to the users is taken into account in this paper. This is another motivation to develop this treatise. More specifically, we investigate the performance of paired users, i.e., the usernand userffor IRS-NOMA-HI networks, in terms of outage probability and system throughput in delay-limited transmission mode. Moreover, the collective impact of HI and residual interference is also considered in the considered networks.IRS-OMA-HI is shown as a comparison benchmark for better evaluation of system performance.Against the previous works, the contributions of the current paper can be summarized as follows:
1. We derive the expressions of outage probability for the usernwith ipSIC/pSIC in IRSNOMA-HI networks over Rician fading channels. To gain the corresponding diversity order,we also derive the asymptotic outage probability expressions in the high SNR region and obtain the diversity orders of the usernwith ipSIC/pSIC schemes. We observe an error floor for the outage probability of the usernwith ipSIC in the high SNR regime.
2. We derive the expressions of outage probability for the userfin IRS-NOMA-HI networks.Based on the asymptotic results, the diversity orders are obtained. We further confirm that the diversity order is connected with the number of IRS elements and the Rician factorK.We also derive the exact expressions of outage probability for IRS-OMA-HI.
3. We evaluate the system throughput of IRS-NOMA-HI and IRS-OMA-HI networks in delaylimited transmission modes. We further compare the outage behaviors and system throughput of users for IRS-NOMA-HI with IRS-OMA-HI. Through extensive simulation results, it is shown that the outage performance and system throughput of IRS-NOMA-HI is superior to that of IRS-OMA-HI.
1.2 Organization
The remainder of this paper is structured as follows. In Section 2, the system model for IRSNOMA-HI is introduced in detail. The expressions of outage probability are derived and the system throughput is studied in Section 3. Furthermore, Section 4 gives simulation results and corresponding performance analysis, followed by conclusions and future directions in Section 5.
2 System Model
We consider an IRS-NOMA-HI network, as depicted in Fig. 1, where one BS communicates with two users via the assistance of an IRS. The two users are classified as the nearby user n and the distant user f, which can receive both the superimposed signal from the BS and the signal reflected by IRS. To simplify the design, the BS and users are equipped with a single antenna while an IRS consists of M configurable elements. Anddenote the phase shifting matrixes, where θm∈[0,2π) is the phase shift of the m-th reflection element.1Note that multiple antennas equipped by the BS and users will further suppress the self-interference and enhance the performance of the IRS-NOMA networks,which are set aside for our future work.All wireless communication channels for the IRS-NOMA-HI networks are assumed to follow the baseband equivalent Rician fading channel models. Note that the channel coefficients from the BS to users, from BS to IRS, and from IRS to users are denoted by hsi, hsr∈CM×1and hri∈CM×1with i ∈(n,f), respectively.2It is worth noting that the nearby user and distant user are distinguished based on the distance from the users to BS.For example,user n are near to BS,while user f are far away from BS.More specifically, letand ˜hsi~C N (0,1), where αsidenotes the large-scale fading coefficients. dsi, ∂and η denote the distance from BS to the user i, path loss exponent and frequency-dependent factor, respectively.The vectors of channel coefficients from the BS to IRS and from the IRS to users are given aswhereand~C N (0,1) with ι ∈(sr,ri). The Rician factor K is the ratio of the power of the direct path signal to the variance of the other multipath power, which reflects the influence of multipath scattering on signal distribution. In particular, the power allocation for the user n and the user f are anand af, satisfying the relationship an+af=1 and an<af. The coherent phase shifting has the ability to improve the performance of IRS-NOMA-HI network, where the phase shift of each reflecting element is matched with the phases of its incoming and outgoing fading channels. This paper chooses coherent phase shifting to simplify computational complexity and provide distinct analytical results. It is worth pointing out that the random phase-shifting of IRS can also affect the outage behaviors, which will be set aside in our future work. To characterize the optimal performance of the IRS-NOMA-HI networks, we assume that the IRS can obtain perfect channel state information of the users.
2.1 IRS-NOMA-HI
The BS simultaneously transmits the signals of two users by adopting superposition coding,and the user n receives both the superimposed signal from the BS and the signal reflected by IRS.Accordingly, the received signal is expressed by
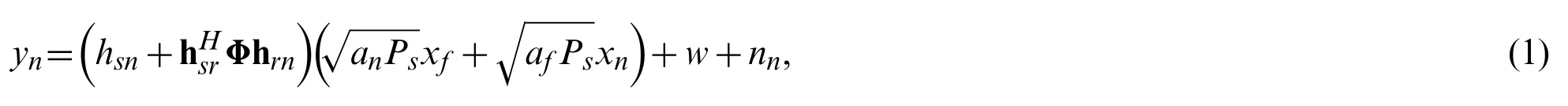
where Psdenotes the normalized transmission power, nndenotes the complex additive white Gaussian noise (AWGN) sample with the mean power N0at user n, and w is HI term and can be modeled by a complex Gaussian distributed random variable with zero mean and finite variance,It is worth noting that kTand kRrepresent the levels of HI at the transmitter and the receiver, respectively. Especially, they are modeled as a complex Gaussian process with zero mean and variancesrespectively.
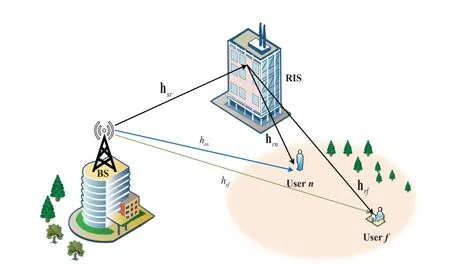
Figure 1: System model for IRS-NOMA-HI networks
According to the NOMA principle, SIC is adopted at usernto detect the information of userf. Therefore, the received signal-to-interference-plus-noise ratio (SINR) at the usernfor detectingxfis given by
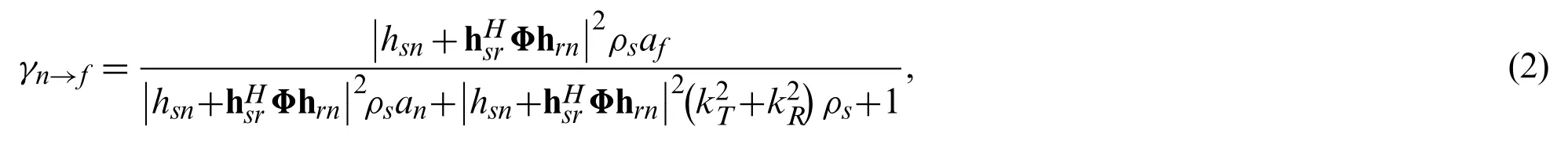
whereis the transmit SNR. After informationxfis detected, it is eliminated from the received signal by performing the SIC process. Thus, the SINR at usernfor detectingxnis given by
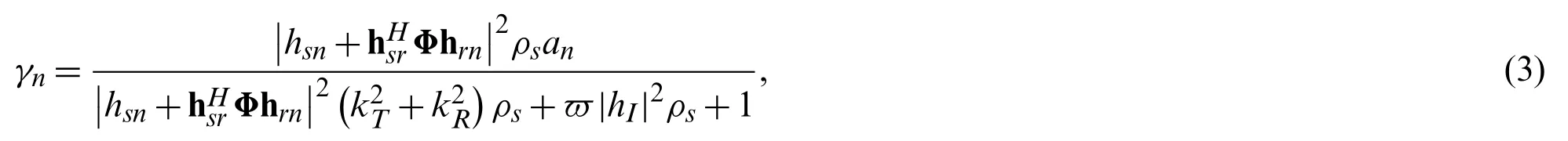
whereϖ=0 and 0<ϖ≤1 denotes the situations of pSIC and ipSIC. Without loss of generality, the complex channel coefficient of residual interference from the ipSIC is denoted ashI~C N (0,ΩI).
With the help of IRS, the received signal at usernis given by
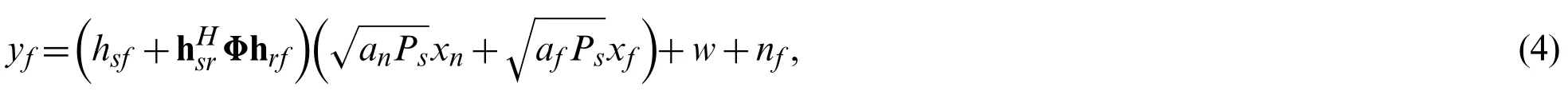
wherenfis the AWGN at userfwith the mean powerN0.
The received SINR to decodexffrom userfcan be given by

2.2 IRS-OMA-HI
In this subsection, the IRS-OMA-HI scheme is used as a benchmark for comparison with the NOMA scheme. The BS transmit a superimposed signal that propagates from the BS for the users through the IRS, the SINR at OMA users can be expressed as

3 Outage Probability
Outage probability metrics are critical to the reliability of transmissions in 6G systems. Hence,this section evaluates the outage performance of the IRS-NOMA-HI network. Specifically, we derive the expressions of outage probability for each user in the pSIC and ipSIC scenarios. Then,we obtain the diversity orders to provide further insights into the communication performance.
3.1 Statistical Channel Characterization
In order to facilitate the derivation of outage probabilities, we characterize the statistical properties of the Rician channel in this subsection.is an random variables (RVs), where the cumulative distribution function (CDF) of Z should be obtained. Letbe an RV, with the probability density function (PDF) can be given by
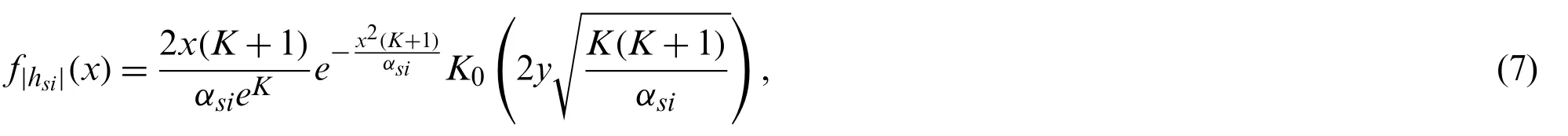
whereK0(·)is the modified Bessel function of the second kind with order zero.
His caretakers said he knew when it was Thursday, even though he knew little else and could not communicate how he knew. He could see, but not speak, could not even sit up unassisted. Yet, he knew when it was his day to go ride. He was only ten, and he didn t live to his teens.
The PDF ofX=is more difficult to calculate. Based on the characteristics of the Rician fading channels, the PDF is obtained using the Laguerre series approximation, which can be approximated as

3.2 Outage Probability for IRS-NOMA-HI
In wireless communication networks, the theoretical analyses of outage probability are the crucial works, which can guide the design and performance optimization of wireless communication systems’practical. In the next part, the outage behaviors of usernand userffor IRS-NOMA-HI networks are investigated in details. Furthermore, it is worth pointing out that implementing MRC in IRS-NOMA-HI transmission will further enhance the performance of IRS-NOMA-HI, which are set aside for our future work.
3.2.1 User n of Outage Probability
For the usern, system communication is interrupted when one of the following two events occurs. Casei)Usernis unable to detect the signalxfof userf; Caseii)Userncannot decode its own signalxnafter detectingxf. Thus, the outage probability of usernfor RIS-NOMA-HI networks is expressed as
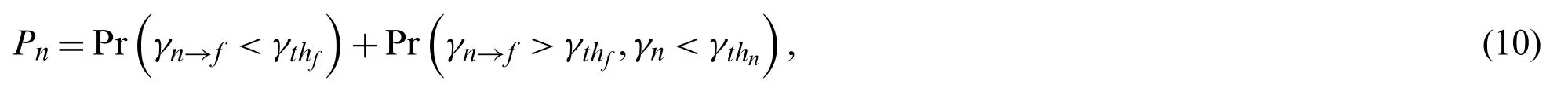
whereγthf=2Rf-1andγthn=2Rn-1denote the SNR threshold of usernand userf. Specially,RnandRfis the target rate at the users to detectxnandxf. The outage probability expression of usernfor the IRS-NOMA-HI isis approximated by the following theorem.
Theorem 1.The expression of outage probability for user f with ipSIC in IRS-NOMA-HI networks is approximated by
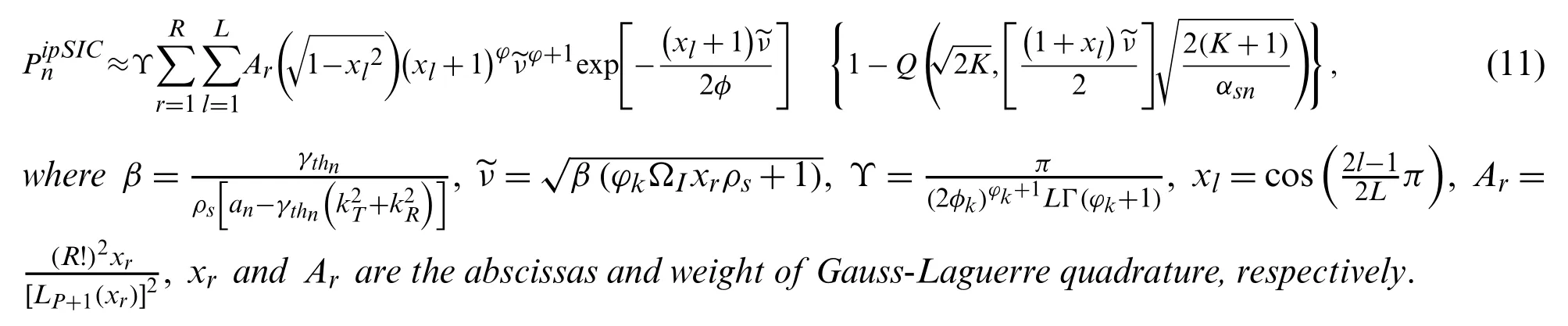
Proof:SeeAppendix A.
Corollary 1.For the particular case ε=0,the expression of outage probability for user f with pSIC in IRS-NOMA-HI networks is approximated by
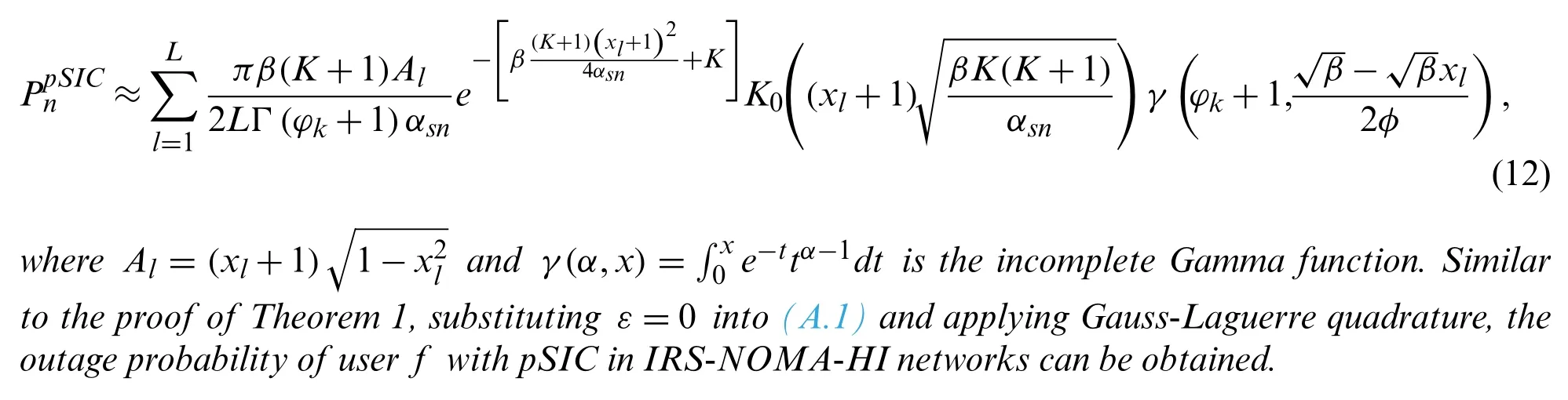
3.2.2 User f of Outage Probability


Proof:SeeAppendix B.
3.3 Outage Probability for IRS-OMA-HI

3.4 Diversity Analysis
To gain more insights, we select the diversity order to evaluate the outage behaviors in the high SINR region [45] based on the above analytical results. In the IRS-NOMA-HI networks, the diversity order is mathematically defined as

whereρsis the transmit SNR, andP∞(ρs)denotes the asymptotic outage probability of the users in the high SNR regime for the considered IRS-NOMA-HI networks, which are summarized in the following corollaries.

Remark 2.Upon substituting (19) into (17) and after some manipulations, the diversity order for the user f with pSIC in IRS-NOMA-HI is obtained as+1.It can be observed that the diversity order of user f with pSIC is in connection with the number of IRS elements and Rician factor K.
Corollary 4.When ρs tends to infinity, the asymptotic outage probability of the user n in IRSNOMA-HI networks is written by
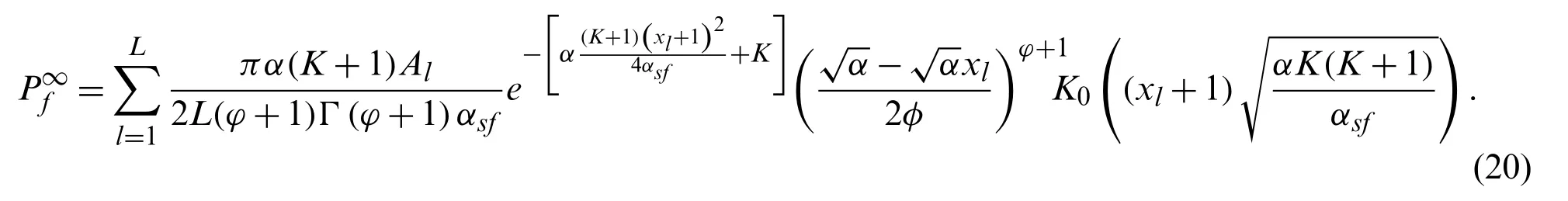
Remark 3.Upon substituting(20)into(17),the diversity order of user n is equal towhich is also related to the number of IRS elements and Rician factor K.
Remark 4.Similar to the proof of the diversity order for IRS-NOMA-HI,the diversity order of user f and user n for IRS-OMA-HI are equal torespectively,which are also related to the number of IRS elements and Rician factor K.
We plotted the diversity order of IRS-NOMA-HI and IRS-OMA-HI networks in a table, as shown in Table 1.
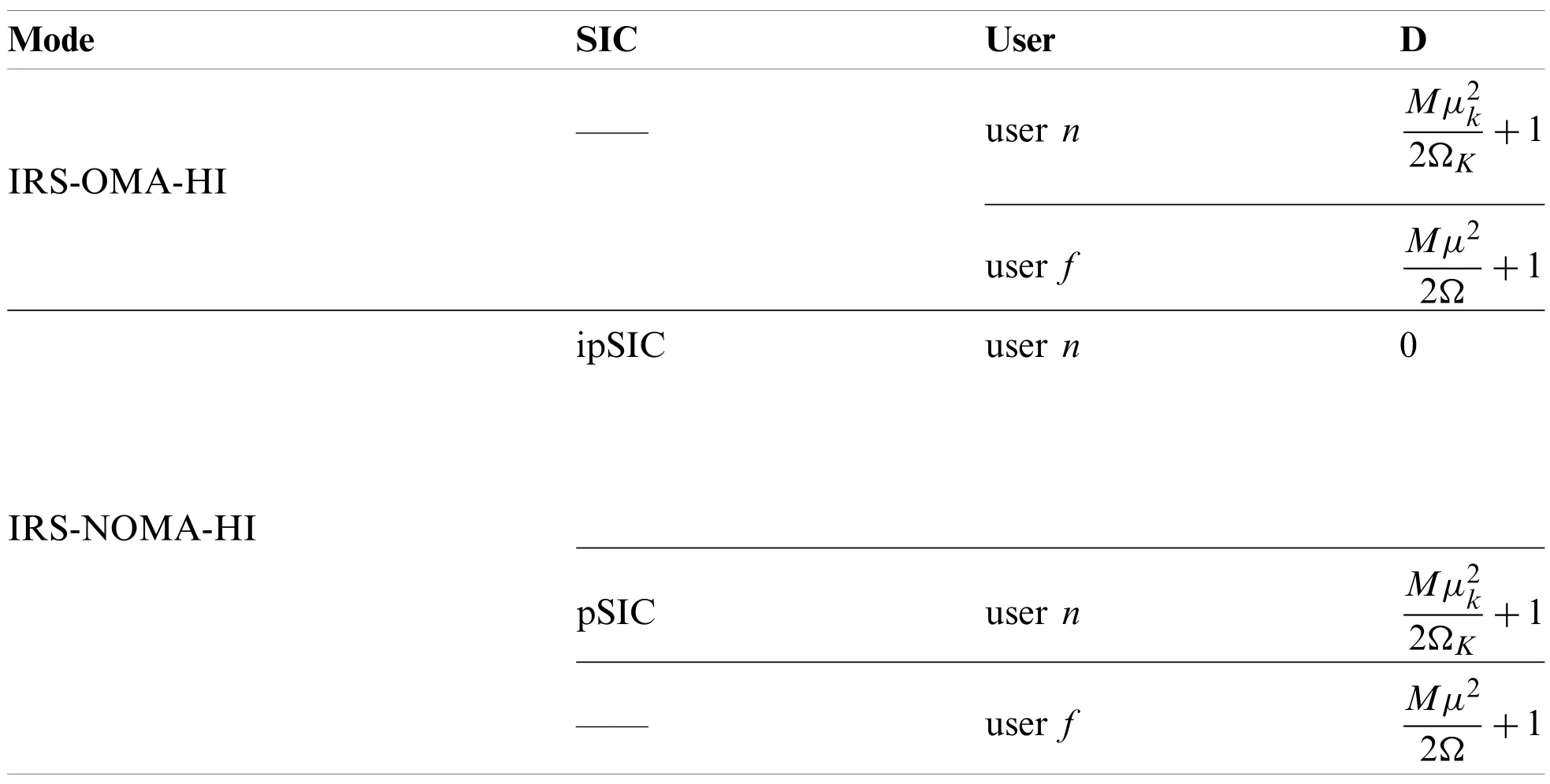
Table 1: Diversity order for IRS-NOMA-HI and IRS-OMA-HI networks
3.5 Throughput Analysis
The system throughput metric is paramount to evaluating the reliability of the transmission in 6G systems. Next, by using the derived results of outage probability above, the delay-limited system throughput of IRS-NOMA-HI networks can be formulated by

whereδ∈(pSIC,ipSIC),andPfcan be obtained from (11), (12) and (14),respectively.
4 Numerical Results
In this section, we aim to confirm through Monte-Carlo simulations the accuracy of our previous mathematical analysis and illustrate the outage performance of the IRS-NOMA-HI networks. To verify the feasibility of the IRS-NOMA-HI networks, IRS-OMA-HI is shown as the comparison benchmarks, and the performance of the transmission schemes is evaluated through computer simulation. The simulation results are averaged over 106realizations. More specifically,the parameters adopted are presented in Table 2 to highlight the performance of the proposed scheme, which is similar to many NOMA research contributions in [10,26,27]. BPCU denotes the short for a bit per channel use and the unit of normalized distancedfor dimensionless physical quantity is generally taken as one. Furthermore, we show the impact of residual interference,target rate, Rician factor and IRS elements on the performance of IRS-NOMA-HI networks. It is worth pointing out that these dots ·are the Monte Carlo simulation values, and the lines are the theoretically derived values.

Table 2: The parameters for numerical results
Fig. 2 plots the outage probability of two users for IRS-NOMA-HI networksvs.the transmit SNR, withM=5,K=5,=-30 dB,Rn=0.03 andRf=0.02 BPCU. For comparison,the outage performance of the traditional IRS-OMA-HI schemes is presented as well. The exact black and red solid curves for the outage probability of usernwith pSIC/ipSIC are plotted according to (11) and (12), respectively. The blue dotted curve for asymptotic outage probability of usernaccording to (18) and (19), respectively. Furthermore, this figure depicts the outage probability of userfin (14)vs.the SNR obtained from the approximate expression in (20) and Monte-Carlo simulations from (13). The exact outage probability cures for the IRS-OMA-HI scheme are plotted according to (16). The simulation is identical to analytical curves across the entire SNR range, which verifies the outage performance. As a benchmark, the outage behavior for IRS-OMA-HI shows the worst performance. The reason is that NOMA differs from conventional OMA by using non-orthogonal communication at the transmitter side and achieving correct demodulation at the receiver side utilizing SIC techniques. The IRS-NOMA-HI has been able to provide higher user fairness relative to IRS-OMA-HI. One can observe that the outage probability with ipSIC converges to an error floor in the high SNR region and obtain a zero diversity order.This is due to the fact that the residual interference from ipSIC for IRS-NOMA-HI, which is also confirmed in Remark 1. Another observation is that the outage behavior of usernwith pSIC outperforms that of usernwith ipSIC and userffor IRS-NOMA-HI networks. This is due to the fact that the usernwith pSIC has access to a larger diversity order than userf, in line with the insights of Remark 2. Due to residual interference, the outage probability of usernwith ipSIC converges to an error floor and the diversity gain is zero. It can also be observed that the outage performance of usernwith ipSIC gets worse as the residual interference value increases.In addition, the outage performance of userncan be improved in the high SNR region, although this user has HI.
Fig. 3 illustrates the outage probability of two users for IRS-NOMA-HI networksvs.the transmit SNR, for a simulation setting withK=5,Rn=0.03 andRf=0.02 BPCU. For high values of the number of IRS elements, the outage probability for IRS-NOMA-HI gains a steeper slope and achieves enhanced outage performance. It is noted that the diversity order found in Remark 2 and Remark 3 depends on the number of IRS elements and the values of HI.This phenomenon indicates the promising integration of IRS technologies in cooperative NOMA communications. Fig. 4 shows the outage probability of two users for IRS-NOMA-HI networks vs. the transmit SNR with different values of target rate. More specifically, the values of Rnare increased from 0.02 BPCU to 0.16 BPCU, and the values of Rfare increased from 0.01 BPCU to 0.12 BPCU. It can be observed that the outage probability decreases with the increase of target rate values.
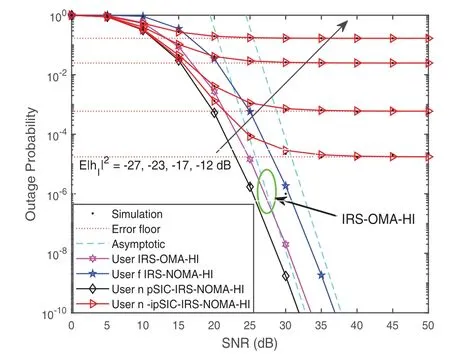
Figure 2: Outage probability vs. the transmit SNR, with Rf =0.03, Rn=0.02 BPCU, M=5, K=5 and =-5 dB
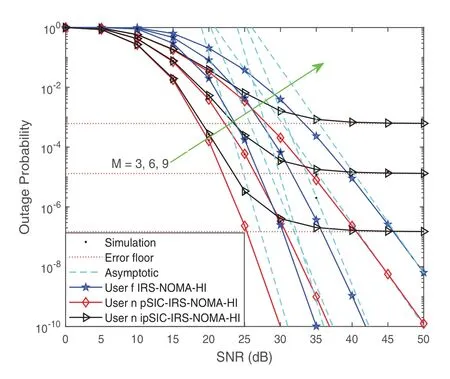
Figure 3: Outage probability vs. the transmit SNR, with the different M
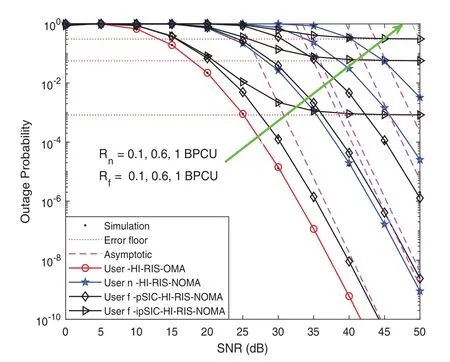
Figure 4: Outage probability vs. the transmit SNR, with the different target rates
Fig. 5 plots the outage probability of two users for IRS-NOMA-HI networksvs.the transmit SNR, withM= 5,K= 5 and= -30 dB. It can be seen that as the Rician factor decreases, the IRS-NOMA-HI network is capable of achieving enhanced outage performance. This phenomenon can be explained by the larger the Rician factorK, the more significant the impact on channel capacity and the increasing damage to the IRS-NOMA-HI network, especially as the SNR increases. As a further advance, Fig. 6 depicts the outage probabilityvs.the transmit SNR, with the different values of pass loss factors. We can observe the influence of the values of pass loss factors on the performance of IRS-NOMA-HI; the higher the values are, the better the performance of the outage probability is. This is due to the fact that the path loss is determined by the radiated spread of the transmit power and the propagation characteristics of the channel,and the channels are mainly influenced by line-of-sight component when the Rician factor is large.
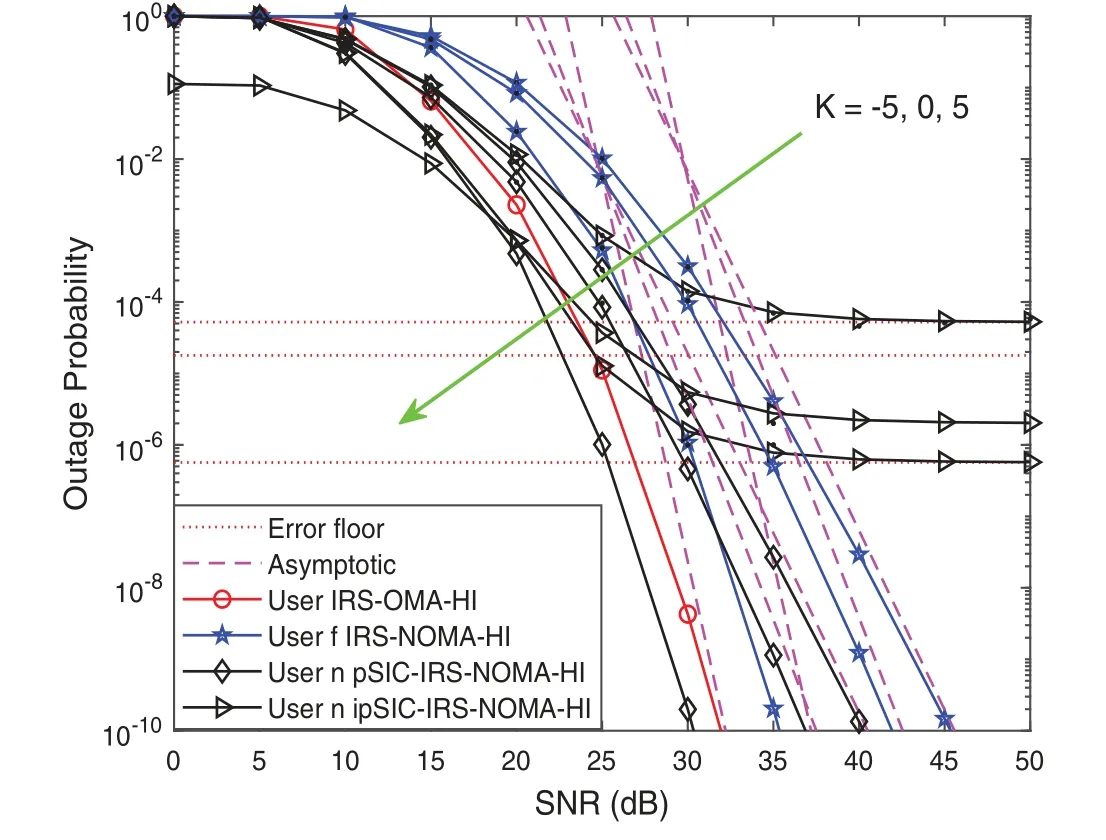
Figure 5: Outage probability vs. the transmit SNR, with the different Rician factors

Figure 6: Outage probability vs. the transmit SNR, with the different pass loss factors
Fig. 7 plots the outage probability of two users for IRS-NOMA-HI networksvs.the transmit SNR, withM=5,K=5 and=-30 dB. It can be observed from the figure that the bad impact of IRS-NOMA-HI networks becomes more severe than the value of HI. The perfect value of HIkT=kR=0 is shown as a benchmark, and the best outage performance can be observed for the ideal case in which both the transmitter and receiver do not experience the impact of HI.It is worth noting the importance of accurately modeling HI at the transmitter and receivers when evaluating the performance of IRS-NOMA-HI networks.
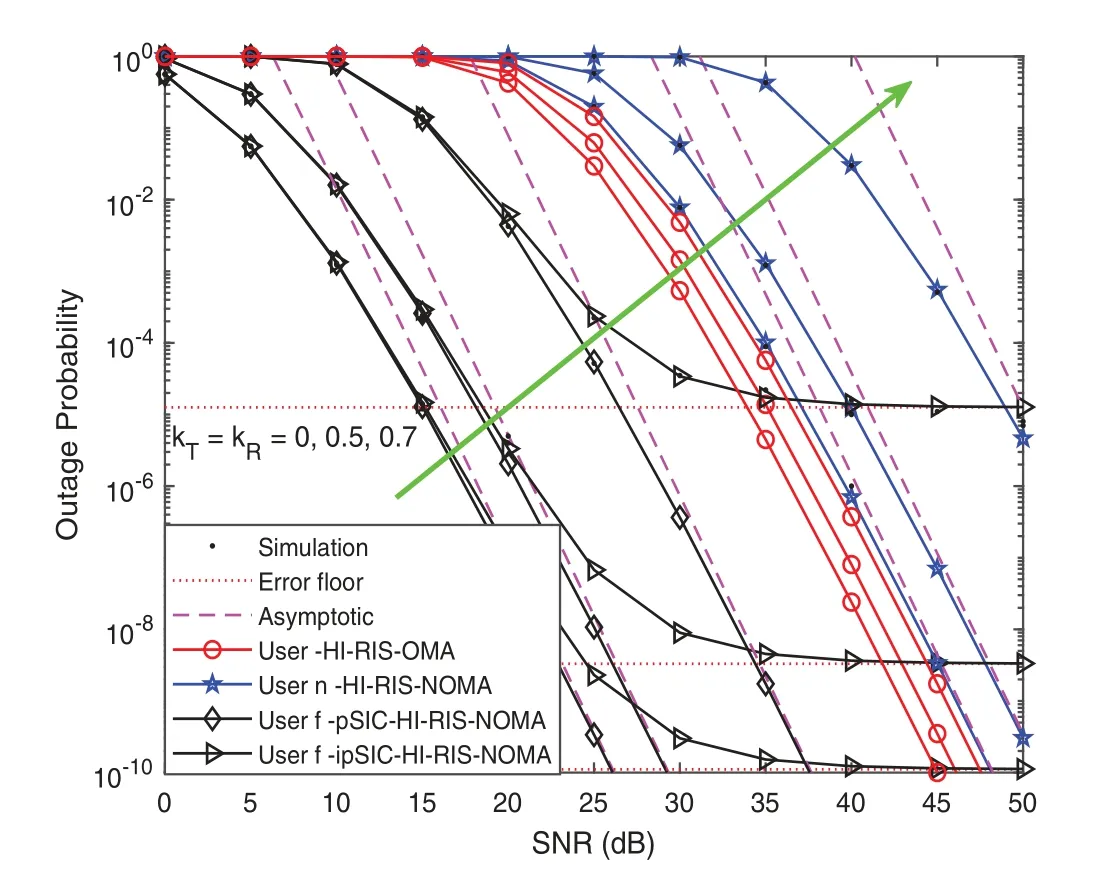
Figure 7: Outage probability vs. the transmit SNR, with the different value of HI
Fig. 8 plots the curve of system throughputvs.the transmit SNR in delay-limited transmission mode, for a simulation setting withRn= 1,Rf= 1 BPCU,M= 5 andK= 5. In this figure, the curves of system throughput with the transmit SNR in IRS-OMA-HI and IRSNOMA-HI schemes are drawn according to (21). It can be observed from the figure that the system throughput for IRS-NOMA-HI in delay-limited transmission mode is better than that of IRS-OMA-HI. It can be explained that the system throughput depends on achieved the outage probability of users. This finding facilitates the design of IRS in wireless systems to cater to mass connections.

Figure 8: System throughput vs. the transmit SNR in delay-limited transmission mode
5 Conclusion
Although NOMA communication can raise the outage performance and capacity of the traditional OMA wireless system, the residual interference generated by ipSIC and HI imposes a detrimental effect on system performance. This paper examined the joint impact of HI and residual interference on the outage probability and system throughput for the IRS-NOMA-HI and IRS-OMA-HI networks over Rician channels. In particular, we derived the exact and asymptotic expressions of outage probability in both pSIC and ipSIC cases and analyzed the diversity orders to evaluate their performance under various scenarios. Based on the numerical results, it illustrated that the outage performance and system throughput of IRS-NOMA-HI outperformed that of IRS-OMA-HI networks, which can be a promising candidate for future systems. It is recommended that more efforts should be made to suppress the effects of HI and residual interference when deploying IRS-NOMA-HI networks in realistic scenarios.
Funding Statement:This work was supported by the National Natural Science Foundation of China under Grants 62071052, 61901043 and theR&DProgram of Beijing Municipal Education Commission under Grant KM202011232003. The work of W. Tang was supported by Scientific Research Projects supported by Talent Engineering Training Funds of Hebei Province under Grant A202101106 and Science and Technology Project of Hebei Education Department under Grant QN2020508.
Conflicts of Interest:The authors declare that they have no conflicts of interest to report regarding the present study.
Appendix A.Proof of Theorem 1
According to the definition of outage probability, the outage probability of usernfor IRSNOMA-HI networks can be expressed by
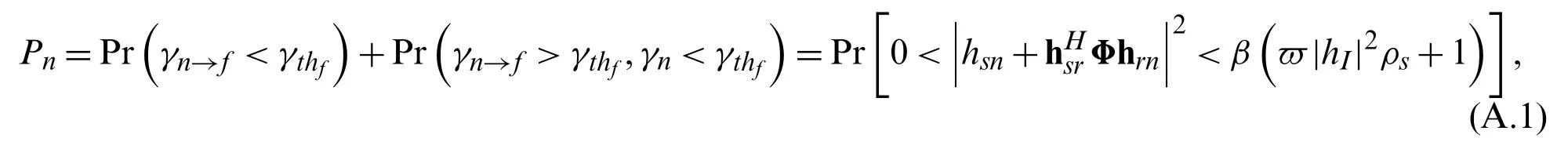
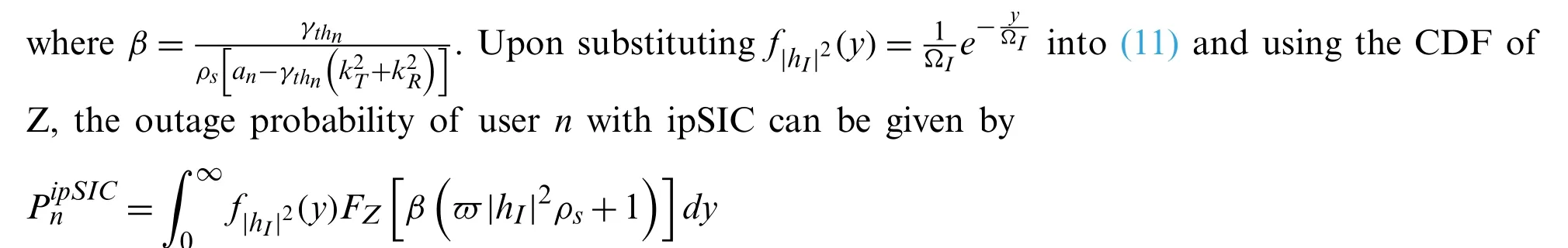
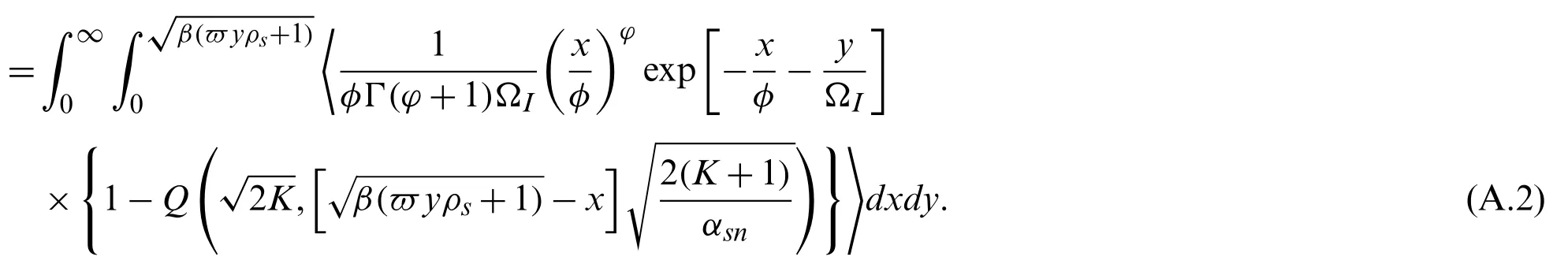
By using the Gauss-Chebyshev quadrature [46], the complex definite integral in the above equation can be approximated as

Appendix B.Proof of Theorem 2
Base on (13), the outage probability of userffor IRS-NOMA-HI networks can be rewritten as

By using the Gauss-Chebyshev quadrature, the outage probability of usernfor IRS-NOMAHI networks can be finally expressed as
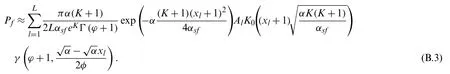
 Computer Modeling In Engineering&Sciences2023年7期
Computer Modeling In Engineering&Sciences2023年7期
- Computer Modeling In Engineering&Sciences的其它文章
- Edge Intelligence with Distributed Processing of DNNs:A Survey
- Turbulent Kinetic Energy of Flow during Inhale and Exhale to Characterize the Severity of Obstructive Sleep Apnea Patient
- The Effects of the Particle Size Ratio on the Behaviors of Binary Granular Materials
- A Novel Light Weight CNN Framework Integrated with Marine Predator Optimization for the Assessment of Tear Film-Lipid Layer Patterns
- Implementation of Rapid Code Transformation Process Using Deep Learning Approaches
- A New Hybrid Hierarchical Parallel Algorithm to Enhance the Performance of Large-Scale Structural Analysis Based on Heterogeneous Multicore Clusters
