Non-Cooperative Behavior Management in Large-Scale Group Decision-Making Considering the Altruistic Behaviors of Experts and Its Application in Emergency Alternative Selection

Mingjun Jiang

Business School,Sichuan University,Chengdu,610064,China

ABSTRACT Emergency decision-making problems usually involve many experts with different professional backgrounds and concerns, leading to non-cooperative behaviors during the consensus-reaching process. Many studies on noncooperative behavior management assumed that the maximum degree of cooperation of experts is to totally accept the revisions suggested by the moderator, which restricted individuals with altruistic behaviors to make more contributions in the agreement-reaching process. In addition, when grouping a large group into subgroups by clustering methods,existing studies were based on the similarity of evaluation values or trust relationships among experts separately but did not consider them simultaneously. In this study, we introduce a clustering method considering the similarity of evaluation values and the trust relations of experts and then develop a consensus model taking into account the altruistic behaviors of experts.First,we cluster experts into subgroups by a constrained Kmeans clustering algorithm according to the opinion similarity and trust relationship of experts.Then,we calculate the weights of experts and clusters based on the centrality degrees of experts. Next, to enhance the quality of consensus reaching, we identify three kinds of non-cooperative behaviors and propose corresponding feedback mechanisms relying on the altruistic behaviors of experts.A numerical example is given to show the effectiveness and practicality of the proposed method in emergency decision-making.The study finds that integrating altruistic behavior analysis in group decision-making can safeguard the interests of experts and ensure the integrity of decision-making information.

KEYWORDS Large-scale group decision making;altruistic behavior;non-cooperative behaviors;consensus reaching;emergency alternative selection

1 Introduction

Over the past decades, emergencies have frequently occurred in China, causing irreversible damage.For example,the massive explosion in Tianjin,China,resulted in the death of 154 people1https://new.qq.com/omn/20210620/20210620A06SFS00.html.;the liquefied gas tanker explosion in Jinyu Petrochemical, resulted in the death of 10 people2https://www.sohu.com/a/211253384_770379..When such an emergency occurs, a high-quality emergency decision-making process can effectively reduce potentially adverse impacts [1]. Usually, emergency decision-making problems have three typical characteristics:time limitation,incomplete information,and decision pressure resulting from potentially serious effects [2,3]. Thus, solving emergency decision-making problems efficiently is definitely a great challenge for both the government and society. Because of the complexity and uncertainty of emergency events,it is necessary to invite experts from different fields and specialties to evaluate alternatives.When the number of experts exceeds 11,it can be regarded as a large-scale group decision-making(LSGDM)problem[4].

Compared with conventional group decision-making problems, LSGDM problems are more complicated,facing many challenges not only in the scale of experts but also in experts’relationships[5].To cope with the scale of an LSGDM problem,the dimensionality reduction which divides a largescale expert team into several subgroups is deemed essential.Clustering analysis is known as one of the most useful dimensionality reduction methods.In this regard,traditional clustering algorithms such as the K-means clustering algorithm[6],fuzzy equivalence relation(FER)[7]and grey clustering[8]have been widely used.However,these methods cluster experts into subgroups based on the opinion similarity of experts but fail to consider the relationships among experts. With the advancement of technology and society,people can communicate and transmit information conveniently,and experts involved in decision-making problems are no more independent individuals.Social network analysis(SNA)has become a common technique for LSGDM problems.To this point,Tian et al.[9]extended the community detection method proposed by Newman et al. [10] to divide large-scale experts in a social network into different communities.Using the trust values between experts,Xu et al.[4]applied the Louvain method[11]based on the idea of modularity to classify experts into different communities in a social network.The above SNA models clustered experts according to the relationships between experts.However,the similarity of evaluation values of alternatives and the trust values between experts both play important roles in grouping experts.Du et al.[12]proposed a trust-similarity analysis(TSA)-based clustering method to manage the clustering operation in LSGDM events.Yu et al.[13]developed a trust-constrained K-means clustering algorithm in a social network large-scale decision-making model. However, in their studies, they only considered a single constraint to overcome the defect of grouping low-trust experts into the same cluster caused by traditional clustering algorithms based on preference similarity,but failed to overcome other problems,for example,high-trust experts may be assigned to different clusters.In this sense,this paper proposes a pairwise trust constrained K-means(PTC-Kmeans) clustering algorithm to cluster experts which considers the similarity of evaluation information of alternatives and the trust values between experts,simultaneously.

Besides,due to different backgrounds and interests,experts in a group may show non-cooperative behaviors in the decision-making process.How to effectively manage the non-cooperative behaviors of experts is another challenge in LSGDM problems[5].To date,many studies[14-18]have considered the non-cooperative behaviors of experts based on the implicit assumption that the full degree of cooperation of experts is to totally accept the revisions proposed by the moderator. However, in actual situations,due to deep trust or close relationships,some individuals may incorporate the wellbeing of others into their own decision even at their own expense. This behavior is named altruistic behavior[19].If an expert has a high degree of trust in another person,he/she may contribute more than a recommendation to protect that person’s interest. In other words, the existence of altruistic behavior may make up for the loss caused by the non-cooperative behaviors of experts[20].Existing literature on non-cooperative behavior management assumes that no one would make more change than the suggested value, which essentially restricts experts with altruistic behaviors from making more contributions to the group consensus.Tang et al.[20]proposed a multi-attribute group decisionmaking (MAGDM) model which utilized the altruistic behaviors of experts to compensate for the adverse effects caused by the non-cooperative behaviors of other experts.However,they only focused on one type of non-cooperative behaviors in their model and did not take the whole problem into account,leading to a lack of integrity.How to incorporate altruistic behavior analysis into the process of consensus reaching and compensate for different types of non-cooperative behaviors are challenges for LSGDM.

Bear all the above analysis in mind, this paper introduces a clustering method considering the similarity of attribute values and the trust relations of experts and then develops a consensus model taking into account the altruistic behaviors of experts. A PTC-Kmeans clustering algorithm is presented to cluster experts into subgroups. After reducing the group size to small communities,we then identify three types of non-cooperative behaviors of experts: 1) experts refuse to adjust their preferences or adjust them slightly, or even change their preferences in an opposite direction;2) hesitant experts randomly provide their preferences to avoid revealing their true intentions; 3)expert deliberately decrease/increase the evaluation value of alternatives. We propose three kinds of feedback mechanisms with respect to three types of non-cooperative behaviors, which allow experts to have altruistic behaviors to compensate for the loss caused by non-cooperative behaviors.The main contributions can be summarized as follows:

(1) This study proposes a PTC-Kmeans clustering algorithm to cluster experts, which considers the similarity of evaluation information given by experts and the trust values between experts,simultaneously.

(2) This study fully considers three kinds of non-cooperative behaviors of experts and distinguishes non-cooperative behaviors based on the differences between expert preferences and cluster preferences.

(3) This paper proposes three kinds of feedback mechanisms with respect to the non-cooperative behaviors of experts, which allows experts to have altruistic behaviors to compensate for the loss caused by non-cooperative behaviors and applies weight penalty mechanisms to decrease the weights of experts with non-cooperative behaviors and increases the consensus level.

The rest of this paper is organized as follows:Section 2 performs a literature review about emergency decision-making and LSGDM methods.In Section 3,we introduce the PTC-Kmeans clustering algorithm to classify a large group of experts into subgroups.Section 4 discusses the management of non-cooperative and altruistic behaviors.We utilize an application example to illustrate the usefulness of the proposed model in Section 5.Concluding remarks are given in Section 6.To better understand this study,the mathematical symbols used in this study are presented in Table S1 in Appendix.

2 Literature Review

In this part, we present the literature review of LSGDM problems. In Section 2.1, we give a snapshot of emergency LSGDM problems. In Section 2.2, we present a short review of clustering algorithms.The review of the advance of SNA for LSGDM is shown in Section 2.3.

2.1 A Snapshot of Emergency LSGDM Problems

When emergencies occur, we often need to make effective decisions in a short period of time.Because of the complexity of emergency problems,time limitations and potential risks,it is difficult for a single expert to solve the emerging problems. Related studies have shown that in emergency decision-making,the decision made by concentrating the wisdom of a group is more reliable than that made by an individual [21,22]. Thus, it is necessary to assemble experts with different backgrounds,experiences and knowledge to make a decision with a high level of consensus.Li et al.[23]proposed an LSGDM model, which adopted fuzzy cluster analysis to integrate heterogeneous information of experts to select the best rescue plan in an emergency situation. Cao et al. [21] proposed a novel opinion formation model that considered psychological factors and relevant opinions in the emergency decision-making process. Liu et al. [24] proposed a method for GDM that introduced an expected multiplicative consistency of incomplete probabilistic linguistic preference relations to avoid the loss of evaluation information of experts and applied the method to address a forest fire rescue problem.Xu et al.[4]proposed a consensus model that considered trust relations and preference risks to manage non-cooperative behaviors in large-group emergency decision-making.

From the above analysis, we can see that current studies have considered different ways to deal with emergency decision-making problems,but seldom considered the non-cooperative behaviors of experts in emergency decision-making problems,and the existing models,which are used to manage non-cooperative behaviors of experts,do not consider the altruistic behaviors of experts.In this study,we shall introduce the altruistic behavior to compensate for the loss caused by the non-cooperative behaviors of experts.

2.2 A Short Review on Clustering Algorithms to Reduce the Dimension of a Large-Scale Group

Clustering analysis has been commonly used to reduce the dimension of many experts in LSGDM problems.A clustering process can divide a large group of experts into several subgroups so that the data in the same cluster is more similar than that from other clusters[25].

As an unsupervised machine learning algorithm,the K-means clustering algorithm is one of the most widely used clustering algorithms.It works by classifying all data objects intokclusters based onkinitial clustering centroids and then iteratively refining them.Wu et al.[26]adopted the K-means clustering algorithm to classify experts with fuzzy preference relations based on the Euclidean distance.Liu et al.[27]introduced the probability K-means clustering algorithm to overcome the weakness that the K-means clustering algorithm is sensitive to the initially selected centroid points,and detected subgroups from the preferences of all experts.In the heterogeneous LSGDM environment,Tang et al.[28]proposed the ordinal K-means clustering algorithm to classify experts into several subgroups.From the above studies,we can see that the traditional K-means clustering algorithm classifies experts mainly based on the similarity among data objects,but ignores the background knowledge from real decision scenarios.

Some experiments have proved that the prior knowledge of objects is helpful for obtaining good clustering results[29].In this regard,Wagstaff et al.[30]proposed a semi-supervised clustering algorithm,the constrained K-means clustering algorithm,which can integrate the background knowledge into the framework of the K-means clustering algorithm. Compared with the traditional K-means clustering algorithm,the constrained K-means clustering algorithm considers two types of constraints,namely, must-link constraints and cannot-link constraints. The must-link constraints specify that two instances must be assigned into the same cluster while the cannot-link constraints indicate that two instances must be in different clusters. Considering the importance of the similarity of experts’evaluation information and the trust values among experts in a clustering process, in this study, we propose the PTC-Kmeans clustering algorithm to cluster the experts into subgroups, which utilizes the trust relations of experts to form must-link and cannot-link constraints.

2.3 Advances of SNA for LSGDM

With the advancement of technology and information, GDM is often conducted within the context of a social network, in which individuals have trust relationships with each other. A social network is composed of a set of nodes and a set of edges, where the nodes represent experts in society and the edges represent the trust relationships among experts. In this study, the nodes are set asE= {e1,e2,···,em} and the edge betweenehandelis set asl(eh,el). A fuzzy social-matrix [8]A=(ahl)m×monEis a relation with a membership functionus:E×E→[0,1], andus(eh,el)=ahl,whereahl∈[0,1]denotes the trust degree that expertehassigns to expertel.

In real LSGDM problems, it is probable that some experts are unable to accurately provide the trust values for other experts.Thus,some studies[31]classify the trust relationships into three types in SNA: direct, indirect and irrelevant trust. The types of trust relationships are shown in Fig.1. In this figure,‘direct trust’means expertehhas a direct trust relationship toward expertel;‘indirect trust’means although there is no direct trust relationship between expertehandel,expertehcan still establish an indirect trust relationship toward expertelthrough other experts; ‘irrelevant trust’means that there is no direct or indirect trust relationship between expertehandel.The existence of indirect and irrelevant trust may cause the incompletion of the sociometric.In this study,indirect trust is calculated with reference to Eqs.(1)-(6) in the article written by Liao et al. [32]. Set the trust degree to 0.01 if there is no direct or indirect relationship between two experts.The value of 0.01 indicates an irrelevant relationship between the two experts.

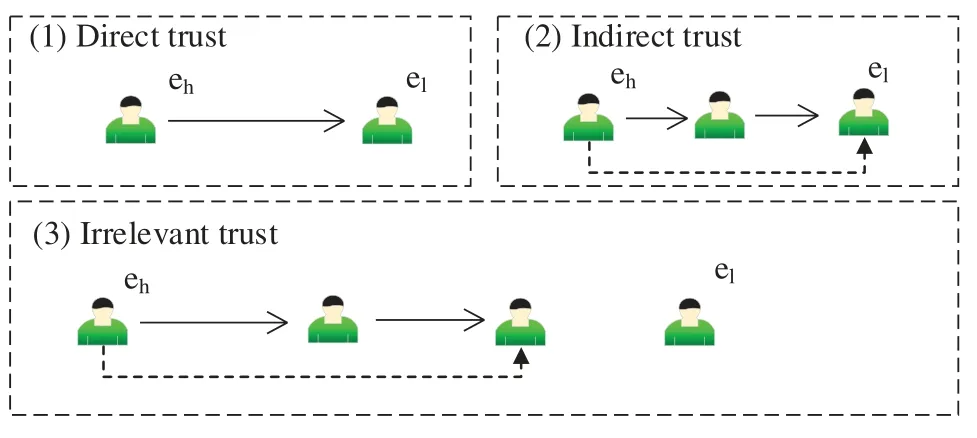
Figure 1:The types of relationship

As a new type of decision-making problem, group decision-making with SNA integrates the trust relations of experts in the process of clustering, consensus reaching and alternative selection[12]. Due to the increasing number of experts in LSGDM, it is difficult to adjust the inconsistent elements and reach a consensus. Experts who come from different fields and represent different interests are likely to display non-cooperative behaviors.The existence of non-cooperative behaviors of experts greatly affects the efficiency of decision-making.Thus,some studies proposed methods to manage non-cooperative behaviors of experts based on the social network.Zhang et al.[18]defined three types of non-cooperative behaviors:1)dishonest behavior;2)disobedient behavior;3)divergent behavior, and proposed an SNA-based consensus framework to manage non-cooperative behaviors.Gao et al.[33]developed a consensus reaching algorithm with non-cooperative behavior management for personalized individual semantics-based social network GDM problem.Li et al.[34]introduced a novel framework based on the WeChat-like interaction social network to manage non-cooperative behaviors of experts.Xu et al.[4]proposed a consensus model based on interval-valued intuitionistic fuzzy numbers,which considered the trust relations of experts in a social network and the preference risks of experts to manage non-cooperative behaviors of experts.

From the above analysis we can see that:1)the trust relationships of experts in a social network are usually used in the clustering process to cluster experts but seldom used in the CRP,2)few studies refine the non-cooperative behaviors into different types,3)most studies analyze non-cooperative behaviors of experts based on the assumption that the greatest degree of cooperation of experts is to totally accept the revisions proposed by the moderator.In this study,to improve the consensus level,we introduce the altruistic behaviors which allow experts to make more contributions than the recommendation proposed by the moderator to compensate for the loss caused by the experts’different types of noncooperative behaviors. What’s more, the trust relationship of experts in a social network serves as a condition to judge whether the experts have altruistic behaviors in the CRP.

3 Grouping Experts by a Semi-Supervised Clustering Processing

To solve an LSGDM problem, it is vital to divide the large group of experts into small communities, so as to simplify the decision process. As justified in the introduction, it is essential to consider the similarity of evaluation information of alternatives given by different experts and the trust values between experts simultaneously when grouping experts.Thus,motivated by the constrained Kmeans clustering algorithm[3],we introduce the PTC-Kmeans clustering algorithm to cluster experts in Section 3.1. Then, the method to determine the weights of experts and clusters is presented in Section 3.2.

3.1 Expert Clustering by the PTC-Kmeans Clustering Algorithm

In typical LSGDM problems,the degree of consistency of experts’preferences is usually regarded as a clustering criterion [35,36]. Such a type of clustering method performs clustering based on group opinions but ignores the trust relationships between experts.In this study,we extend the trustconstrained K-means clustering algorithm [13] and utilize the trust values of experts as constraints to cluster experts.Assume that a set of experts,E= {e1,e2,···,em},(m≥11),are invited to conduct evaluation information on a set of emergency alternatives,X={x1,x2,x3···,xn},(n≥2).

3.1.1 The Constraints

The PTC-Kmeans clustering algorithm is mainly a constraint-based K-means clustering algorithm.So,we firstly consider two types of constraints,namely must-link constraint and cannot-link constraint.

In this study,we set constraints based on the trust relationship between experts.Because the trust value provided by an expert is directional,which means the trust value between two experts may be unequal.In other words,expertehhas a high trust value to expertel,but expertelmay trust expertehto a low degree.Therefore,we divert the directed trust degree into undirected trust degree between any two experts.

Letλ=(λ1,λ2,···,λm)Tbe a weight vector such thatλi∈[0,1]and= 1.The average trust degree between expertehand expertelis calculated as:

where 0 ≤mahl≤1,mahl=malh, and min{ahl,alh}≤mahl≤max{ahl,alh}.

To simplify,we denote the aggregated social-matrix asMA=(mahl)m×m.

The trust constraints formulate that a pair of experts with a low average trust value cannot be allocated in the same cluster and a pair of experts with a high average trust value must be allocated in the same cluster.

Let the threshold of trust constraints beCon1,Con2,whereCon1,Con2∈[0,1].If the average trust valuemahlbetween expertehand expertelis lower thanCon1,it means that they are cannot-linked.If the average trust valuemahlbetween expertehand expertelis higher thanCon2,it means that they are must-linked.

LetΩ=(Ωhl)m×mbe a cannot-linked constraint matrix,such that

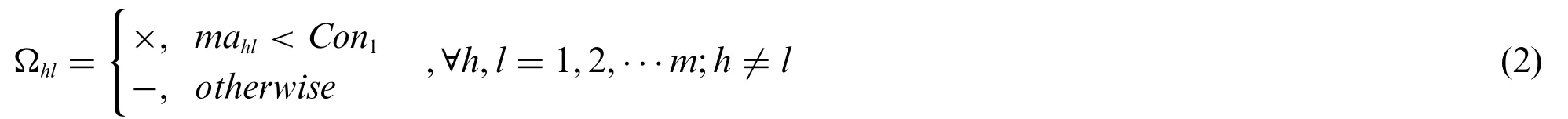
IfΩhl=×,it means that expertehand expertelshouldn’t be classified into a same cluster.

LetΨ=(Ψhl)m×mbe a must-linked constraint matrix,such that

3.1.2 The PTC-Kmeans Clustering Algorithm

Once the constraints are defined, experts can be clustered into subgroups according to the similarity degrees of experts’evaluation information based on the constraints.

Definition 1[13]:Measure the similarity degree of evaluation information between expertehand expertel.LetPeh=and=be two FPRs of expertehand expertel.Here,we use the Euclidean distance to measure the similarity degree between two FPRs. Then, the similarity degreesdhlbetween the two experts can be calculated as

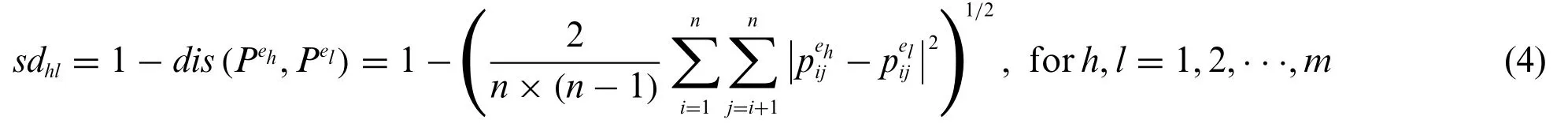
wheresdhl=sdlh,0 ≤sdhl≤1.Then,the similarity matrixSD=(sdhl)m×minvolving all experts can be established.

where#Ckmeans the number of experts in clusterCk.

The main steps of the PTC-Kmeans clustering algorithm are presented in Algorithm 1.

Algorithm 1:The PTC-Kmeans clustering algorithm Input:The number of clusters k,FPRs,the fuzzy social-matrix A,the cannot-link matrix Ω and the must-link matrix Ψ.Output:The clusters C1,C2,···,Ck.Step 1:Initialize k clusters C1,z,C2,z,···,Ck,z where z is the number of clustering iterations and set the initialized value as 0, z = 0. Then, we determine the clusters C1,0,C2,0,···,Ck,0 with the condition that Ωhl = - between any two experts in cluster Ck,0, and if Ψ = √between any two experts,we regard the two as an integrated one.Step 2: Calculate the similarity degree between expert eh and cluster center Qk according to Eq.(4),and assign expert eh to the closest cluster Ck,z satisfying that the constraint Ω(eh,Ck,z) =0.Step 3:Update the cluster center Qk of cluster Ck,z.Iterate Step 2.Step 4:Stop when Ck,z =Ck,z+1.

3.2 Weight Determination of Experts and Clusters

After the large-scale experts are divided into several clusters,the weights of experts and clusters should be determined.Centrality is an essential indicator to judge the influence,status and importance of an expert in a social network.We gain the weights of experts using the concept of centrality.The degree of centrality ofeh∈Ecan be computed by averaging the trust degrees obtained byehas below:

The weightλhof expertehis defined as:

Clearly,0＜λh ＜1, and=1.

The weight of a cluster is calculated based on the sum of the weights of the experts in the cluster.The weightμkof clusterCkcan be calculated as:

4 Feedback Mechanism Based on Non-Cooperative and Altruistic Behaviors

Section 4.1 presents the process of measuring the consensus degree of clusters and the whole group. In Section 4.2, we discuss the methods to identify three types of non-cooperative behaviors of experts,and altruistic behavior is introduced to reduce the degree of uncooperativeness of experts in Section 4.3.Then,a feedback mechanism is shown in Section 4.4.A punishment mechanism is used to decrease the influence of non-cooperative behaviors of experts in Section 4.5. Finally, we present the algorithm of the proposed LSGDM model in Section 4.6.

4.1 Consensus Measurement

LetPCk=×nbe an FPR of the clusterCk,which can be obtained by aggregating the FPRs of the experts in the clusterCk,

where#Ckdenotes the number of the experts in the clusterCk.

The distance betweenehandCkis calculated as:

Then,the degree of consensus of the expertehcan be computed as:

The degree of consensus of the clusterCkis:

The degree of consensus of the whole groupcg(C)has the same calculation process as the degree of consensus of the cluster,which is shown as:

A thresholdθforcd(Ck), and a thresholdδforcg(C)should be set in advance. Ifcd(Ck)≥θandcg(C)≥δ, the global group reaches the acceptable consensus level, then we can select the optimal alternative of the LSGDM problem.Otherwise,a feedback mechanism is applied to improve the consensus level. Here, we should note that a low consensus threshold may lead to controversial decisions while a high consensus threshold may result in the increasing of decision-making cost and the waste of time. The value of the threshold mainly depends on the specific problems. We should set a large value of the threshold such as 0.9 when a decision-making problem is critical; due to the time limitation,we should set a lower consensus threshold such as 0.8 in emergency decision-making problems[9].So,in this study,we setθ,δas 0.8.

4.2 Non-Cooperative Behaviors Identification

4.2.1 Non-Cooperative Behavior Caused by Expert Who Refuse to Follow the Revision Proposals

In the CRP,in order to achieve the ideal consensus level among experts,experts need to modify their individual preferences based on the suggestions received.However,some experts may refuse to adjust their preference information or adjust them slightly,or even change their preference information in the opposite direction.In this study,this type of behavior can be defined as the first kind of noncooperative behavior(NCB-I).

whererepresents the deviation between the actually adjusted evaluation value in position(i,j)made by expertehand the adjusted evaluation value recommended by the moderator,andDAR(eh,z)denotes the sum of deviations between the actually adjusted evaluation value made by expertehand the adjusted evaluation value recommended by the moderator in roundz.

The non-cooperative indexof expertehin roundzcan be defined as:

4.2.2 Non-Cooperative Behavior Caused by Experts Deliberately Concealing Their True Intentions

In the CRP, some hesitant experts may randomly provide their preferences to avoid revealing their true intentions,which can make experts’adjusted opinions further away from the opinion of the subgroup. In this study, this type of behavior can be defined as the second kind of non-cooperative behavior(NCB-II).

4.2.3 Non-Cooperative Behavior Caused by Experts Who Deliberately Lower the Ranking of the Optimal Alternative Obtained in the Whole Group

In the CRP,some experts may be purposed to decrease the evaluation value of the most preferred collective alternative in the whole group and lead to a drop in the ranking of the optimal alternative in the whole group.In this study,this type of behavior can be defined as the third kind of non-cooperative behavior(NCB-III).x3≻x2≻x1orx2≻x3≻x1,the experteαis judged to have NCB-III.Thus,the thresholdS2is set as 0.33.

4.3 Altruistic Behavior Analysis

Because of some intimate relationships, some individuals may consider the well-being of others in the decision-making process even at their own expense [20]. In this study, we allow the expert to have altruistic behavior,which means he/she can contribute more than the recommended modification provided by the moderator.Because the consensus level of the cluster is obtained by aggregating the consensus levels of all the experts in the cluster,the altruistic behaviors of some experts can compensate for the loss caused by others’non-cooperative behaviors in the same cluster.In other words,altruistic behavior can reduce the adverse effect of the non-cooperative behaviors of experts on decision-making results.

4.4 Feedback Mechanism

Ifcd(Ck)≥θ,cg(C)≥δ,the consensus levels of the cluster and the whole group have reached the threshold. Otherwise, the experts whose consensus levels do not reach consensus threshold in the cluster require revising their opinions to increase the degree of consensus level of the cluster.A feedback adjustment mechanism is used to help the experts update their preferences to increase consensus level. If an expert has non-cooperative behaviors and other experts do not have altruistic behavior toward him/her or to a small degree, the expert will be subject to a weight punishment to reduce his/her negative influence on group decision-making.

4.5 The Punishment Mechanism for Non-Cooperative Behaviors

If no expert in clusterckis willing to show altruistic behavior towards expertehor to compensates only part of the loss caused by the non-cooperative behavior of experteh, then a punishment mechanism will be introduced to adjust the weight of experteh.

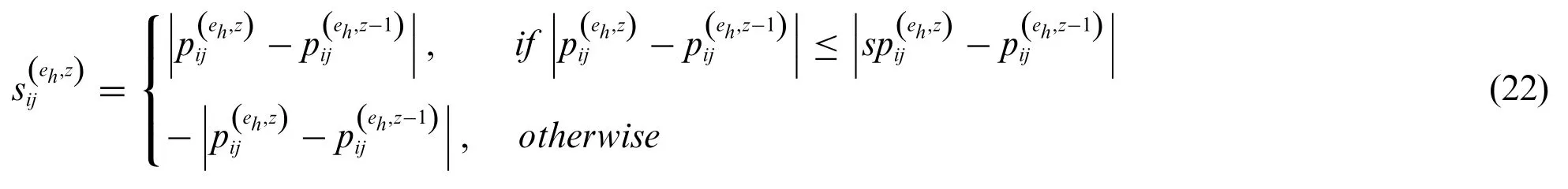
And letSEhbe the actually total number of adjusted values of expertehin the clusterCk,it can be calculated as:

Suppose that the experts in the clusterCkwho agree to make more contributions to make up for the loss ofehconstitute a setM,M⊂Ck.LetRAEhbe the sum of adjusted values that other experts contribute to experteh.It can be computed as:

The altruistic index is defined as:

We determine the coefficient of the weight penalty based on the non-cooperative index and the altruistic index,with a step size of 0.2.BecauseAIh∈[0,1]means other experts has totally or partially compensated for the loss caused by experteh,thus we use the central valueAIh=0.5 as a demarcation value.The adjusted weightλhof expertehis denoted as:

(1) if the expertehhas the NCB-I:

(2) if the expertehhas the NCB-II:

(3) if the expertehmatches the NCB-III:

If expertehhas two or more non-cooperative behaviors,the adjusted weight isNormalize the weights.Then the normalized weight of the expertehcan be calculated as:

4.6 Algorithm of the Proposed LSGDM Model

For better understanding, we provide the detailed steps of the proposed model as Algorithm 2.Fig.2 shows the flow chart of the proposed method.

Algorithm 2:An LSGDM model based on the social network Input:The internal FPRs, the fuzzy social-matrix A, the number k of cluster, the threshold θ, δ and the parameters S1 and S2.Output:The ranking of alternatives.Step 1:Obtain a complete social-matrix of experts.Step 2:Cluster experts into clusters by the PTC-Kmeans clustering algorithm.Step 3:Obtain the weights of experts and clusters by using Eqs.(7)and(8).Step 4:Calculate the consensus levels of clusters and experts.If all the clusters’consensus levels reach the threshold cd(Ck)≥θ,then go to the Step 6;otherwise,go to the next step.Step 5:Apply the punishment mechanisms for the experts with non-cooperative behaviors to improve the consensus levels of clusters.Identify the types of the non-cooperative behaviors of experts and analyze the altruistic behaviors of experts.Step 6: Calculate the consensus level of the whole group. If cg(C) ≥δ, then go to the next step;otherwise,return to Step 5.Step 7: The final group preference matrix PC is obtained using Eq.(10). The alternatives are then ranked and the optimal one is selected.

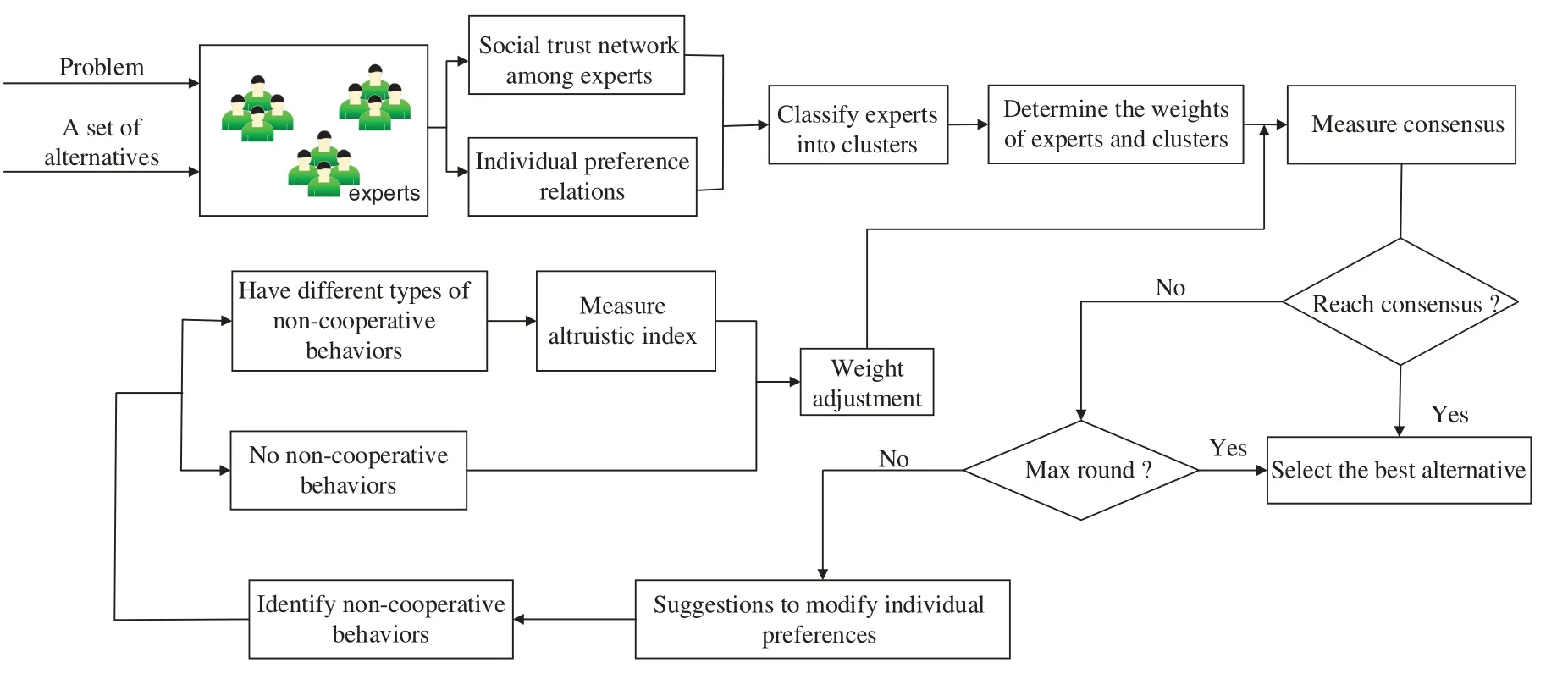
Figure 2:The flow chart of the proposed model

5 Case Study:Emergency Alternative Selection after the Flood

In this section,to demonstrate the usefulness of the proposed model,we apply the model into a case study regarding the selection of emergency alternative after the flood in Henan,China in 2021.

5.1 Case Description

From July 16 to July 2021,heavy rainfall affected 287,713 people in 140 towns and villages in 31 counties and districts in Henan,China.It caused directed economic losses of RMB 104.6047 million,resulted in 302 deaths and 50 missing3http://henan.sina.com.cn/news/2021-08-02/detail-ikqciyzk9115688.shtml..In order to reduce the damage caused by the disaster,Henan Province Flood Control and Drought Relief Headquarters reacted quickly, made saving people a priority,and initiated the second-level response of flood control emergency plan.More than 28,000 rescue teams in Henan Province, 19 city-level commando teams for fire-fighting and flood rescue,157 station-level attack teams which has a total of 3790 firefighters and 366 rescue boats assembled in advance,and strived to rush to the scene as soon as the disaster occurred4https://www.163.com/dy/article/GFDNN7OC0514R9L4.html..An emergency headquarters composed of 15 experts was established. After analysis, three alternatives were initially identified:X={x1,x2,x3}.

x1: Set up Rescue Assault Squads to go deep into the disaster area to know about the situation as soon as possible, and guide the people in the disaster area to rescue themselves. Simultaneously,firefighters are dispatched to reinforce important locations such as major rivers, reservoirs and dams,and rescue teams are dispatched to repair communication and power facilities.After receiving information from the Rescue Assault Squads,further rescue work will be carried out.

x2: Quickly organize a certain number of firefighters and rescue boats to carry out rescue work in the disaster area and organize the transfer of the affected people. Simultaneously, firefighters are dispatched to reinforce important locations such as major rivers,reservoirs and dams,and rescue teams are dispatched to repair communication and power facilities.

x3: Let the medical rescue teams to enter the disaster area with the Rescue Squads, so as to rescue the injured person as soon as possible.Simultaneously,firefighters are dispatched to reinforce important locations such as major rivers, reservoirs and dams, and rescue teams are dispatched to repair communication and power facilities. After receiving information from the Rescue Assault Squads,further rescue work will be carried out.

5.2 Resolving Process

Step 1:Obtain the experts’evaluation information, trust relationship and establish a complete social network.

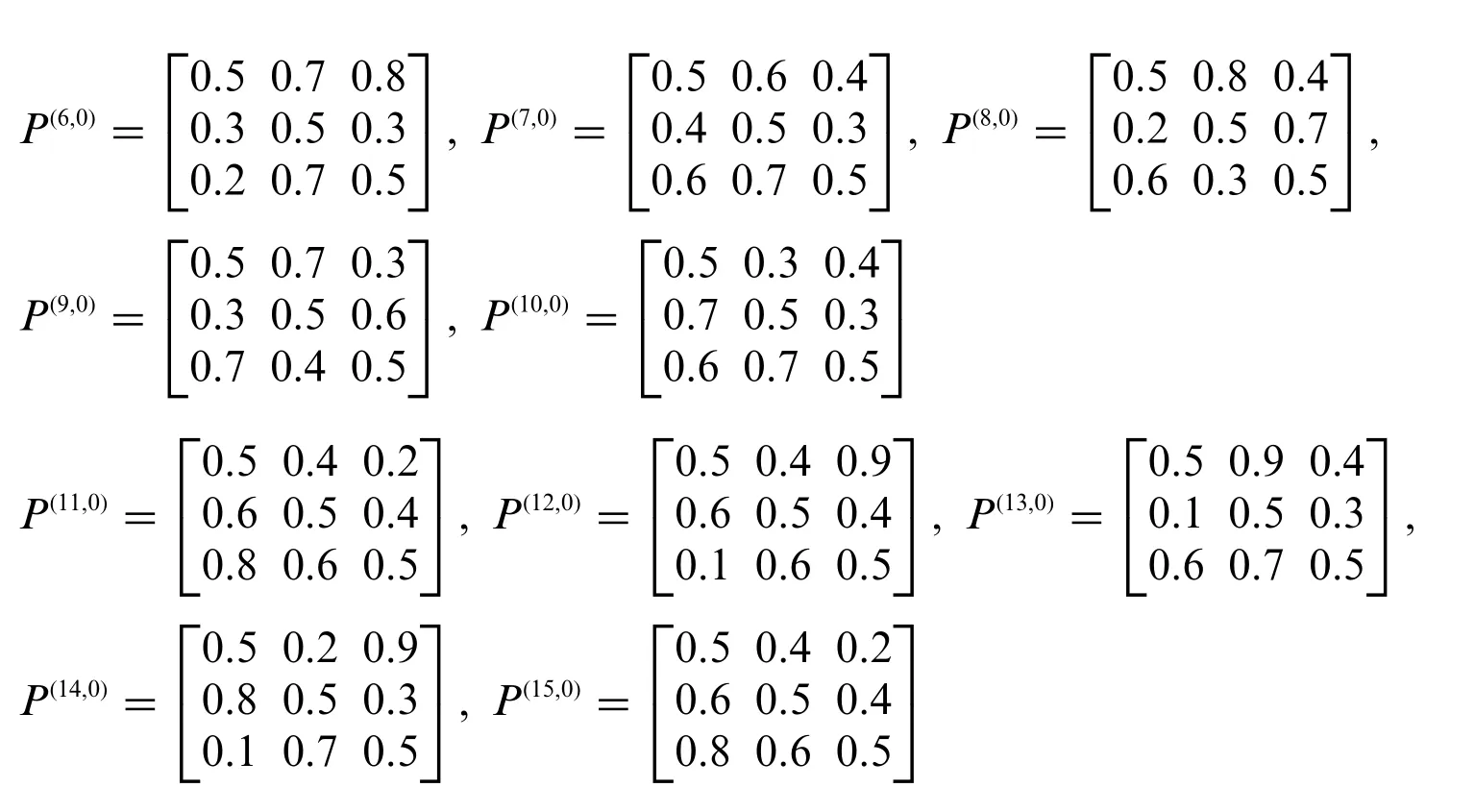
The initial FPRs of the 15 experts are shown as follows:

The direct and indirect trust relationships of experts are presented in Fig.3.

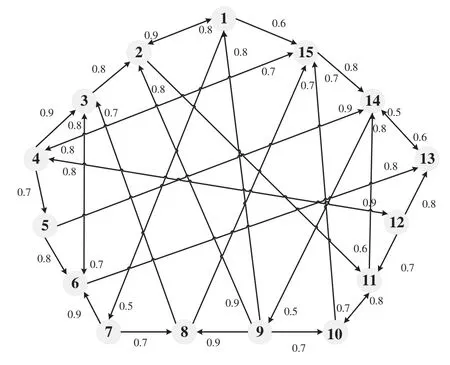
Figure 3:The social network of 15 experts

According to Eqs.(1)-(6)in the article by Liao et al.[32],we can struct a complete social network.The social-matrix among 15 experts is:

Step 2:Classify the large group of experts into subgroups.

According to Eq.(1),we calculated the aggregated social-matrixMA=(mahl)m×m.SinceMAis a symmetric matrix,we only show the upper triangular matrix.

The PTC-Kmeans algorithm is used to cluster the experts.In this case,we assign the cannot-link constraint thresholdCon1= 0.15 and the must-link constraint thresholdCon2= 0.85. The number of clustersk= 4. The clustering results areC1= {e3,e14},C2= {e4,e5,e6,e13},C3= {e7,e8,e9} andC4={e1,e2,e10,e11,e12,e15}.

Step 3:Calculate the weights of experts and clusters.

According to Eq.(7),we can obtain the weights of experts and the results are shown in Table 1.

Table 1: The weights of experts

According to Eq.(8),we can obtain the weights of the clusters:μ1= 0.17,μ2= 0.26,μ3= 0.16 andμ4=0.41.

According to Eq.(9),we can obtain the FPRs of clusters:

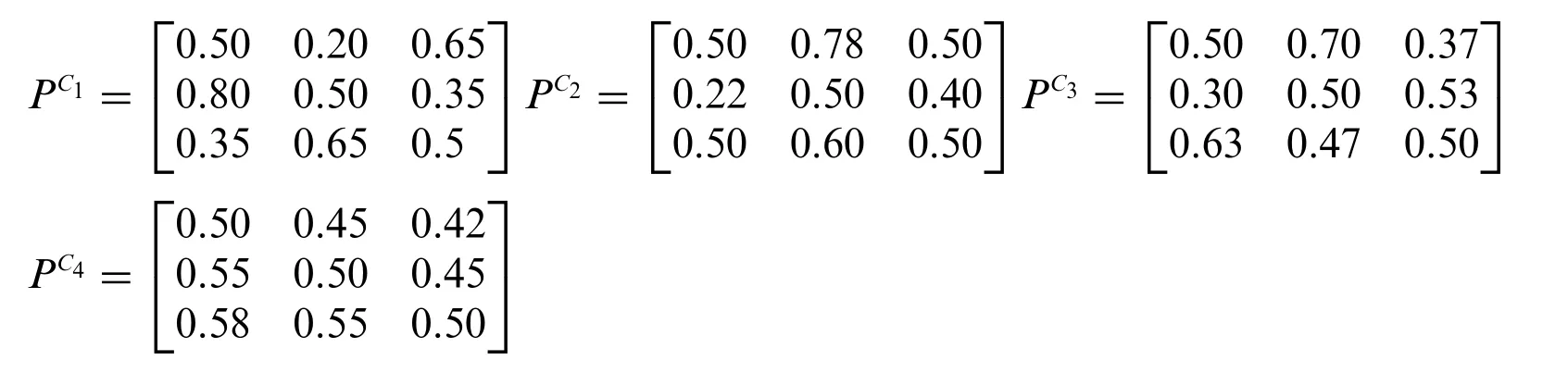
According to Eq.(10),we can obtain the FPR of the whole group:

Step 4:Consensus measurement. Eq.(13) are used to compute the degree of consensus of each cluster.The initial consensus levels are shown in Table 2.We set the clusters’consensus threshold asθ=0.80.

Table 2: Initial consensus levels of clusters and experts

From Table 2, we can see that the consensus levels of clusterC2andC4are lower than the thresholdθ=0.80.Thus,for clusters whose consensus level is lower than the threshold,the preference information of experts within the cluster should be modified.

Step 5:Apply the feedback mechanism.

The first consensus round

Since the consensus levels of expertse4,e6in clusterC2and expertse1,e11,e12,e15in clusterC4fail to reach the thresholdθ,these experts should adjust their own opinions according to the suggestions recommended by the moderator. The actual adjustment preference matrixP1, and the preference matrixSPrecommended by the moderator are shown in Table 3.

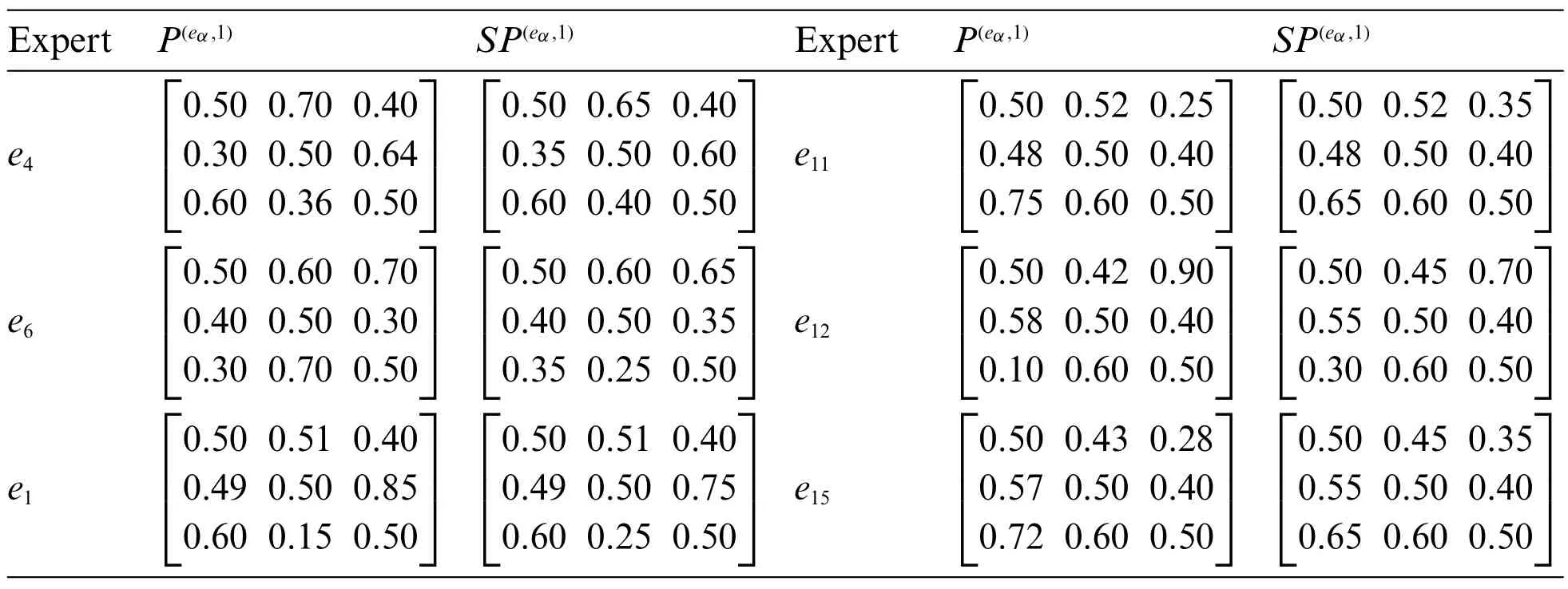
Table 3: The actual adjustment preference matrix and the preference matrix recommended by the moderator

Let the parameterS1= 0.5 andS2= 0.33,the non-cooperative indexes of the experts with noncooperative behaviors are calculated according to Eqs.(15)-(21).The results are shown in Table 4.

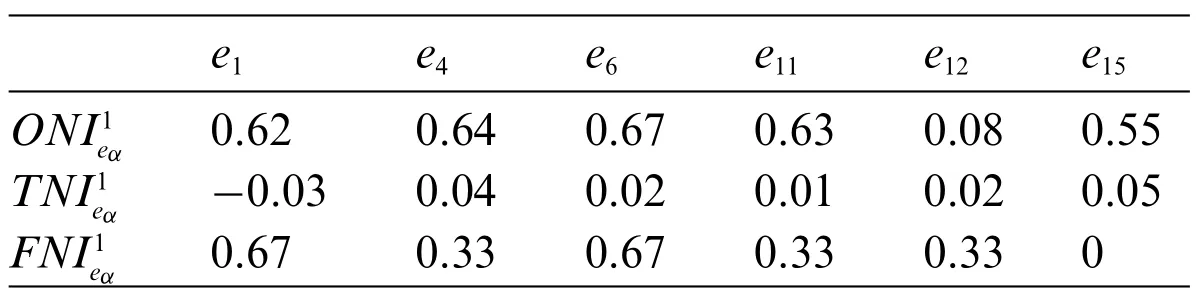
Table 4: Non-cooperative indexes

The second consensus round

From the first consensus round,we know that the consensus level of clusterC4is lower than the thresholdθ= 0.80. Thus, the preference information in clusterC4should continue to be modified.Due to the consensus levels of experte1,e12in clusterC4are lower than the threshold,the two experts should continue to adjust their preference information according to the suggestions recommended by the moderator.

The adjusted FPRs of expertse2ande12recommended by the moderator in round 2 are:

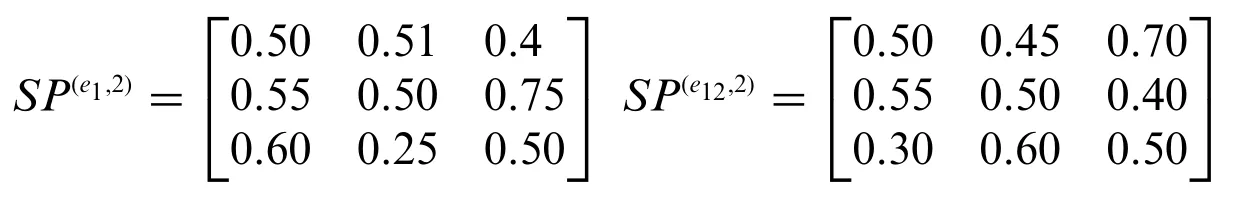
The actual adjusted FPRs of expertse2ande12are:

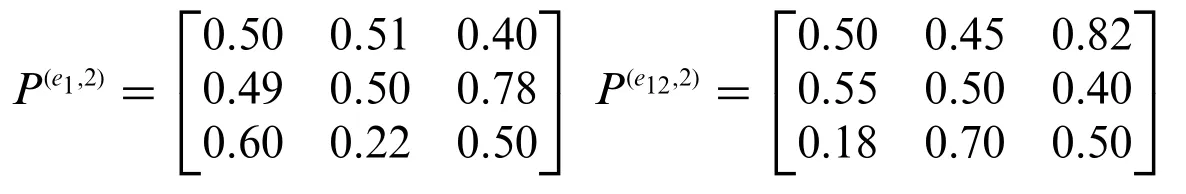
Then,the non-cooperative indexes are calculated.The non-cooperative indexes of the experts with non-cooperative behaviors are calculated according to Eqs.(15)-(21).The results are shown in Table 5.

Table 5: Non-cooperative indexes

Due to1in Table 5,we infer that experte12exists NCB-I.Ande15would like to make more contributions to make up for the loss caused by the non-cooperative behavior of experte12.The altruistic index of experte12is calculated as=0.42.Experte12suffers weight punishment according to Eq.(26).The weights of experts are updated as:

λ2=(0.067,0.089,0.079,0.081,0.053,0.072,0.038,0.057,0.085,0.064,0.068,0.024,0.082,0.112,0.029).

The consensus levels of clusters are calculated as:cd(C1)= 0.83,cd(C2)= 0.81,cd(C3)= 0.85 andcd(C4)= 0.83.To show the CRP visually,we list the change of consensus level of clusters in the iterative process in Fig.4.

Step 6:Calculate the consensus level of the whole group.

Set the thresholdδ= 0.80 in advance.Using Eq.(14),the consensus level of the whole group is calculated as:cg(C)=0.82.

Step 7:Selection of alternatives.

From Step 5 and Step 6, we can see thatcd(Ck)≥θ,cg(C)≥δ. The final collective decision matrix is obtained according to Eq.(10):

The alternatives are ranked as:x3≻x1≻x2,x3is thus the optimal alternative.

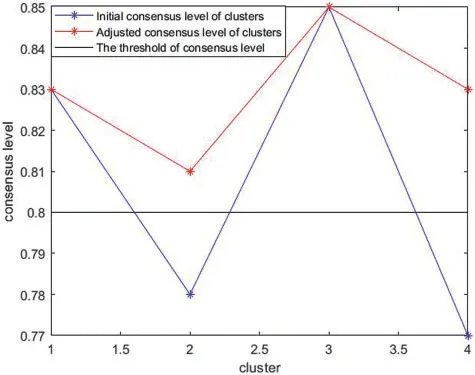
Figure 4:Changes in the consensus levels of clusters

5.3 Comparisons and Discussions

To further reflect the advantages and features of our proposed model, we conduct comparative analysis and discussion as follows:

5.3.1 Discussion on the PTC-Kmeans Clustering Algorithm

1) Determination ofk

We use the sum of the squared errors(SSE)to determine the value ofk.The core idea of SSE is:as the number of clusterskincreases,the division of the samples will be more refined,the aggregation degree of each cluster will gradually increase,and the value of SSE will naturally become smaller.Whenkis less than the optimal clustering number,since the increase ofkwill greatly increase the aggregation of each cluster,the decline of the value of SSE will be very large.Whenkreaches the optimal clustering number,the decline of the value of SSE will be slight with the increase ofk.The SSE is shown as:

wheremimeans the centroid of the clusterCi.

Fig.5 presents the relationship between SSE and the number of clusters. When the number of clusters is more than 4,the SSE decreases slightly.Thus,we setk=4 as the number of clusters.

Figure 5:Relationship between SSE and the number of clusters

2) Determination of the trust constraints thresholdsCon1,Con2

The trust constraints play crucial roles in the determination of the initial clusters and the final cluster results. As shown in Fig.6, the trust constraint threshold is positively correlated with the number of cannot-links while the threshold is negatively correlated with the number of must-links.The greater the number of cannot-links,the greater the minimum number of initial clusters,and the smaller the number of must-links,the greater the maximum number of initial clusters.For example,if there are 15 cannot-links,then it is possible that the minimum number of clusters required is 15;if there are 15 must-links,then it is possible that the maximum number of clusters is 1.In order to ensure that we can obtain 4 initial clusters,the cannot-link trust constraint link is set tocon1∈[0,0.15]and the cannot-link trust constraint link is set tocon2∈[0.8,1].Specifically,we setcon1=0.15,con2=0.85.

Figure 6:The relationship between the trust constraint threshold with the number of constraint links

3) Comparison with the traditional K-means algorithm

Where our algorithm differs from traditional algorithms is the addition of trust constraints. In our algorithm,experts with low trust should not be allocated to the same cluster while those with high trust must be in the same cluster.Through directly numerical comparison with the traditional K-means clustering method,the advantages of our algorithm are highlighted.As shown in Table 6,the overall trust degree and the consensus level of the initial clusters obtained by our proposed method are both higher than the initial clusters obtained by the traditional K-means.A higher degree of consensus level means a fewer number of positions to be adjusted.The decision cost of our proposed method is lower than the traditional K-means.

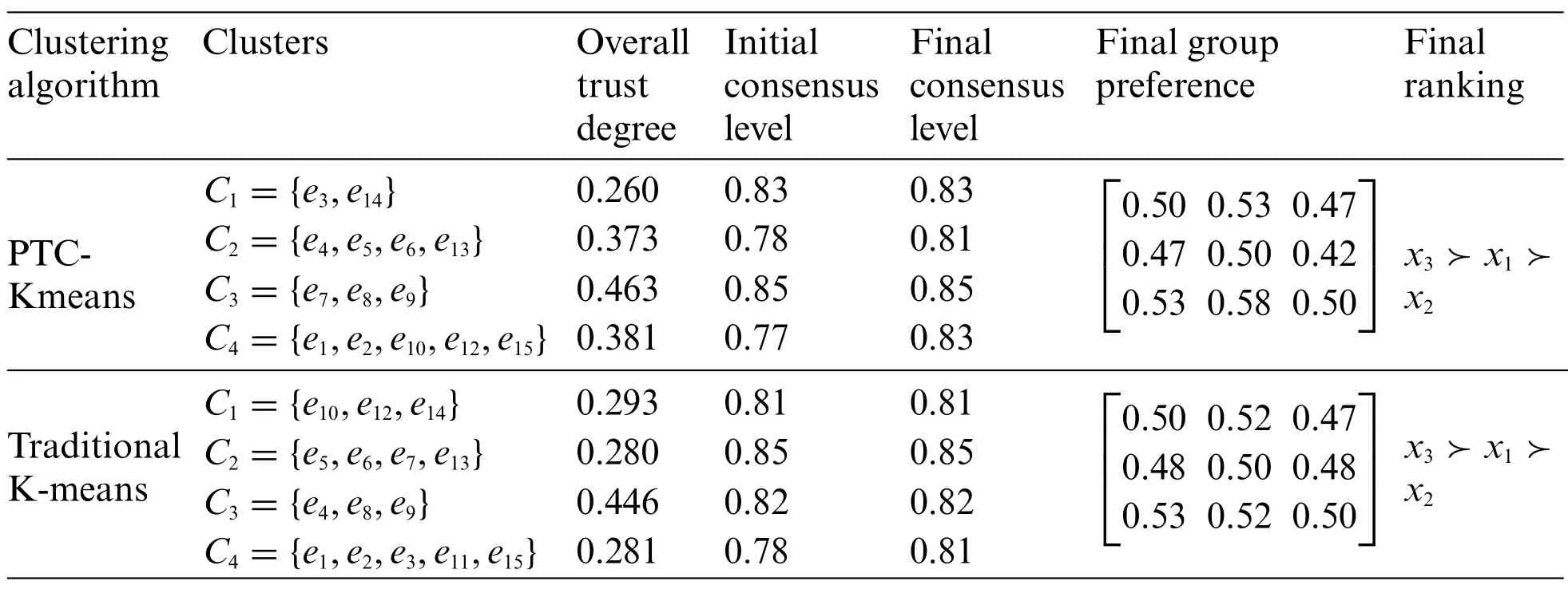
Table 6: Comparison with the traditional K-means algorithm

5.3.2 Discussion on the GDM Models

1) We use the data from the first consensus round in Section 5.2 to compare changes in the weight of experts when considering altruistic behavior and not considering altruistic behavior.Fig.7 shows the difference in the weights of experts with altruistic and non-altruistic behaviors.We can see that when considering the altruistic behaviors of experts, the adjusted weight of experts is closer to the initial weight of experts than without altruistic behavior. It indicates that considering altruistic behavior not only can protect the interests of experts with noncooperative behavior but also ensures the integrity of group opinions.

2) The comparisons with the management of non-cooperative behaviors in GDM models are demonstrated in Table 7.Compared with Tang et al.[20],Liao et al.[37],they only considered one type of non-cooperative behaviors. It can lead to a lack of integrity as they did not consider the whole problem.In our study,we define three types of non-cooperative behaviors.Dong et al. [15] also focused on different types of non-cooperative behaviors. However, in their models,they did not cluster the experts into subgroups and they assumed the maximum degree of cooperation is to totally accept the modification suggestions. For the definition of non-cooperative behaviors, they did not consider such a behavior that hesitant experts are purposed to provide their preference randomly to avoid revealing their true intentions.In this paper, we used the PTC-Kmeans algorithm to cluster experts into different subgroups and managed the non-cooperative behaviors based on different clusters.What’s more,we allowed experts to make more contributions to make up for the loss caused by experts with the noncooperative behaviors,it protected the interests of experts with non-cooperative behaviors and ensured the integrity of decision-making information. We set different weight punishment according to the degree of non-cooperative and the degree of altruism.

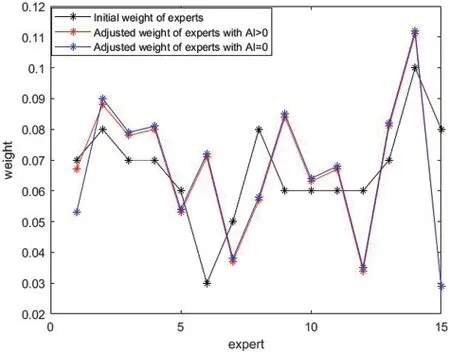
Figure 7:Changes in the weight of experts when considering altruistic behavior and not considering altruistic behavior

Table 7: Comparisons with the management of non-cooperative behaviors in GDM models

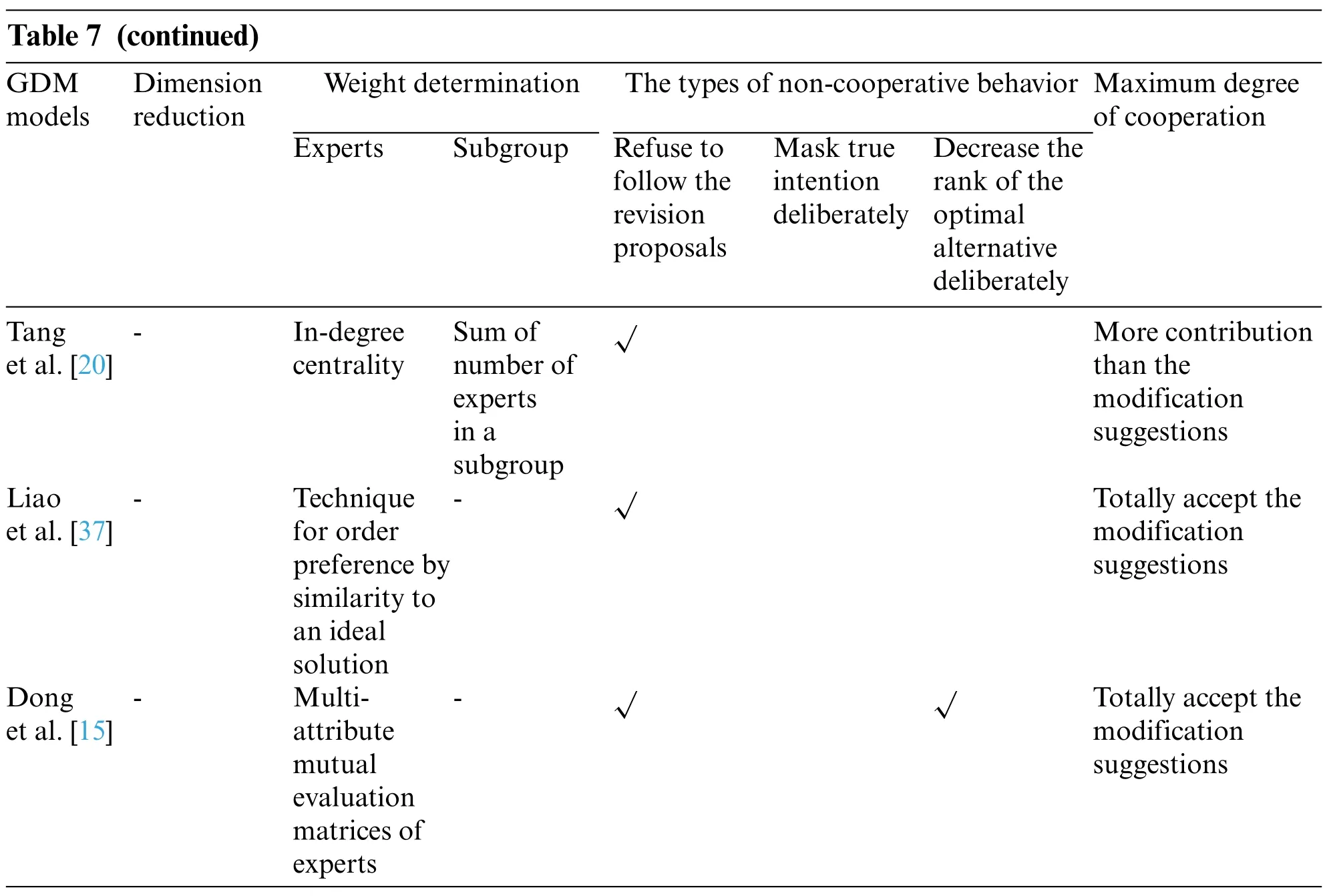
Table 7 (continued)GDM models Dimension reduction Weight determination The types of non-cooperative behavior Maximum degree of cooperation Experts Subgroup Refuse to follow the revision proposals Mask true intention deliberately Decrease the rank of the optimal alternative deliberately Tang et al.[20]-In-degree centrality Sum of number of experts in a subgroup√More contribution than the modification suggestions Liao et al.[37]-Technique for order preference by similarity to an ideal solution-√Totally accept the modification suggestions Dong et al.[15]-Multiattribute mutual evaluation matrices of experts-√√Totally accept the modification suggestions

6 Conclusion

In this study,we proposed a consensus reaching model based on the social network which took into account different types of non-cooperative behaviors and altruistic behavior of experts in LSGDM problems. The main contributions and improvements could be summarized as follow: 1) the PTCKmeans algorithm was proposed to classify experts into several clusters based on the individual FPRs and trust relationships of experts. The two attributes were all regarded as important basis for classification and were seldom considered simultaneously in existing clustering methods. 2) A consensus reaching approach was proposed to improve the consensus level.Such a consensus reaching approach considered different types of non-cooperative behaviors and allowed experts with altruistic behaviors to make more contributions to compensate for the loss caused by the experts with noncooperative behaviors.Different types of non-cooperative behaviors allowed for a more comprehensive consideration of the problem and the existence of altruistic behavior ensured the interests of experts with non-cooperative behavior.3)The proposed LSGDM method was applied to a case study of the selection of emergency alternative after the flood in Henan,China.

There are still some limitations in this study. First, we only considered the non-cooperative behavior of experts but failed to consider the cooperative behavior.However,the cooperative behavior of experts may also affect the decision-making. Second, we did not take the cost control into consideration in the LSGDM.In the future,it is necessary to study how to merge altruistic behavior of experts into minimum cost consensus model.In addition,we assumed that all the experts used FPRs to express their preference information,in the future research,it is necessary to present the preference information of experts in more complex representations.

Funding Statement:The work was supported by the National Natural Science Foundation of China(Nos.71771156,71971145,72171158).

Conflicts of Interest:The author declares that they have no conflicts of interest to report regarding the present study.

Appendix

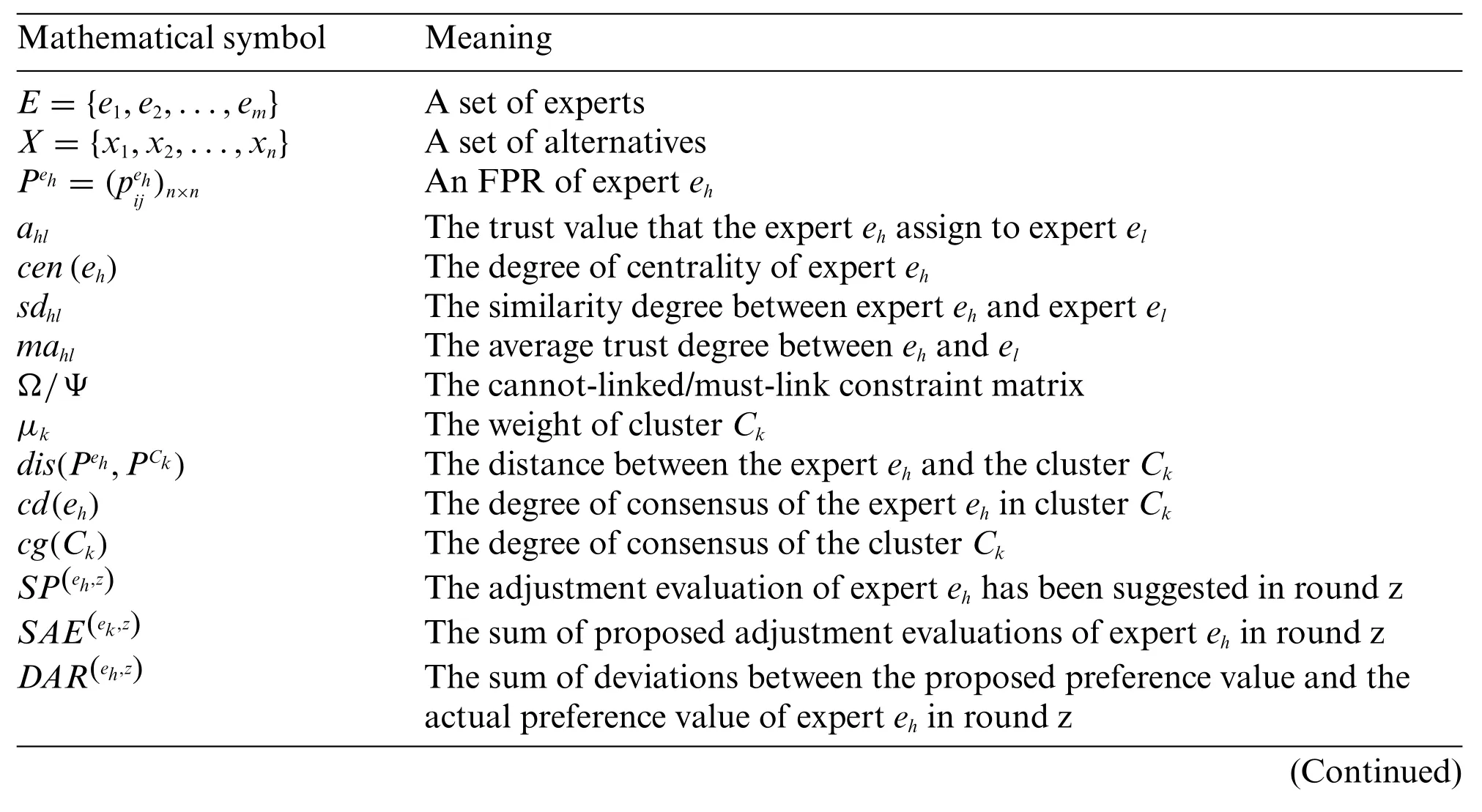
Table S1: A summarization of mathematical symbols

Table S1 (continued)Mathematical symbol Meaning ONIzh/FNIzh/TNIzh The index of NCB-I/II/III of expert eh in round z SEh The actually total adjusted evaluation values of expert eh in round z RAEh The sum of evaluation values eh has been made contribution by other experts AIh The altruistic index of expert eh