时频分析和深度学习相结合的滚动轴承故障诊断

任胜杰, 郭伟超, 舒定真, 汤奥斐, 高新勤, 李言

(西安理工大学 机械与精密仪器工程学院,西安 710048)

滚动轴承作为旋转机械的核心部件,用于支撑旋转体在传动系统中传递扭矩和动力,其健康状况会对机构的性能、稳定性和使用寿命产生严重的影响[1]。避免因为轴承故障引起设备非正常运行最有效的方法是在设备运行过程中对轴承工作状态进行实时监控,及早发现故障,进行维护或更换。在对设备运行状态长期监测的过程中,通过对采集的信号进行处理和分析,提取时域、频域和时频域内的故障特征量[2],然后通过主成分分析、独立成分分析和判别分析等进行特征降维,去除无用和不敏感的信息而保留有用的特征信息,最后将提取的特征信息输入支持向量机、K-近邻算法、决策树、高斯混合模型和多特征决策树集成等分类器进行故障分类[3]。这种方法广泛用于机械设备的故障识别领域,但是这种方法最大的缺点是人为干预比重太大,对识别结果影响较大。

而深度学习作为机器学习的一个分支,模仿人的分析、学习能力,可以直接处理图像[4]、文本[5]和声音[6]等数据,不需要人为过多干预就能解决复杂的模式识别问题,近年来越来越多的应用于机械设备和机构的故障识别中,并取得了显著效果。如Saravanan等[7]基于深度学习理论,使用离散小波变换进行特征提取,利用深度学习网络成功对齿轮箱的故障进行了识别;Gondal等[8]提出了一种基于深度学习的轴承故障诊断方法,该方法使用预处理的FFT频谱图像作为人工神经网络(Artificial neural network, ANN)的输入,相比传统人工提取特征在准确率上有大幅度提升;Guo等[9]提出一种基于改进算法的新型分层学习速率自适应深度学习卷积神经网络。该方法在轴承故障类型和故障尺寸评估方面均取得较好的效果。

深度学习虽然无需手动选择相关特征,模型会在数据流经网络时自动完成特征提取和选择任务。但是从零开始搭建深度学习网络需要非常大的数据样本,对于少量故障样本学习能力不强;同时,整个训练过程包括复杂的网络搭建和超参数调节,这需要耗费大量的时间和设备资源[10]。而迁移学习(Transfer learning, TL)能将某个领域内学习到的知识和模型应用到不同但是相关领域内的问题中[11]。如Li等[12]利用迁移学习将源机器学习到的故障知识快速迁移到目标机器,成功对两个滚动轴承数据集进行实验,进一步验证了迁移学习可以应用于相似领域问题的求解。利用迁移学习的这个特性,可以利用已标识的数据来训练深度神经网络模型,然后把训练好的深度神经网络模型,应用于相似领域内问题的求解。利用迁移学习相结合的深度神经网络模型不用从零开始训练,而只需要在预训练网络模型的基础上对新的样本进行训练,对网络参数进行微调,就可以方便、快捷地获得满意的识别效果。这为机器学习和深度学习模型的建立提供了一个新思路。如Chen等[13]提出一种基于深度神经网络(Deep neural network, DNN)的迁移学习故障诊断网络,将网络部分参数迁移至目标任务,与传统无迁移学习的神经网络进行对比,该方法可以在少量样本数据的前提下实现对早期轴承故障的有效诊断。

通过以上应用,可以看出深度学习已经成功应用于故障诊断领域,并且取得了显著的成绩。但是目前在轴承故障诊断领域,影响深度学习广泛应用的最大障碍仍然是如何建立高精度的故障诊断模型[2,14-15]。针对这个问题本文提出一种基于信号时频分析和深度学习相结合的方法来构建滚动轴承故障诊断模型,进而来提高滚动轴承故障诊断识别的准确率。首先,利用十种不同时频方法对轴承故障信号进行分析,获得对应的时频图;然后,通过AlexNet网络单独训练十种时频图,有效地对滚动轴承故障进行诊断,最高准确率可达100%;最后,通过与文献[3]和文献[15]对比,验证了本文模型具有更好的负载适应能力和抗噪性。

1 时频分析

1.1 数据增强

在实际故障识别应用中,通常存在实际采集的故障数据量不足的问题,导致故障诊断模型泛化性能不高。本文借鉴计算机视觉处理,利用重叠采样方法增加训练样本数量以提高模型泛化性能[15]。具体方法如下:

如图1所示,当采样频率为12 kHz,采样时间为1 s,则采样信号总长为120 000个数据点。通过对训练样本重叠采样,若单个样本的长度取850个数据点,设定移动步长为150,根据式(1)计算出获得的训练样本数量为795个。

图1 利用重叠采样进行数据增强

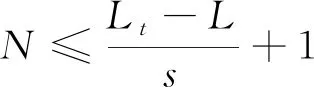
(1)

式中：N为样本数量;Lt为采样信号长度;L为单个样本信号长度;s为每次移动步长。

1.2 十种不同时频分析方法

不同的时频图像对故障的表现程度不一样,会直接影响轴承故障模型的分类精度。因此,选择合适的时频分析方法对轴承故障诊断具有重要意义。本文采用的10种不同的时频分析方法如表1所示。

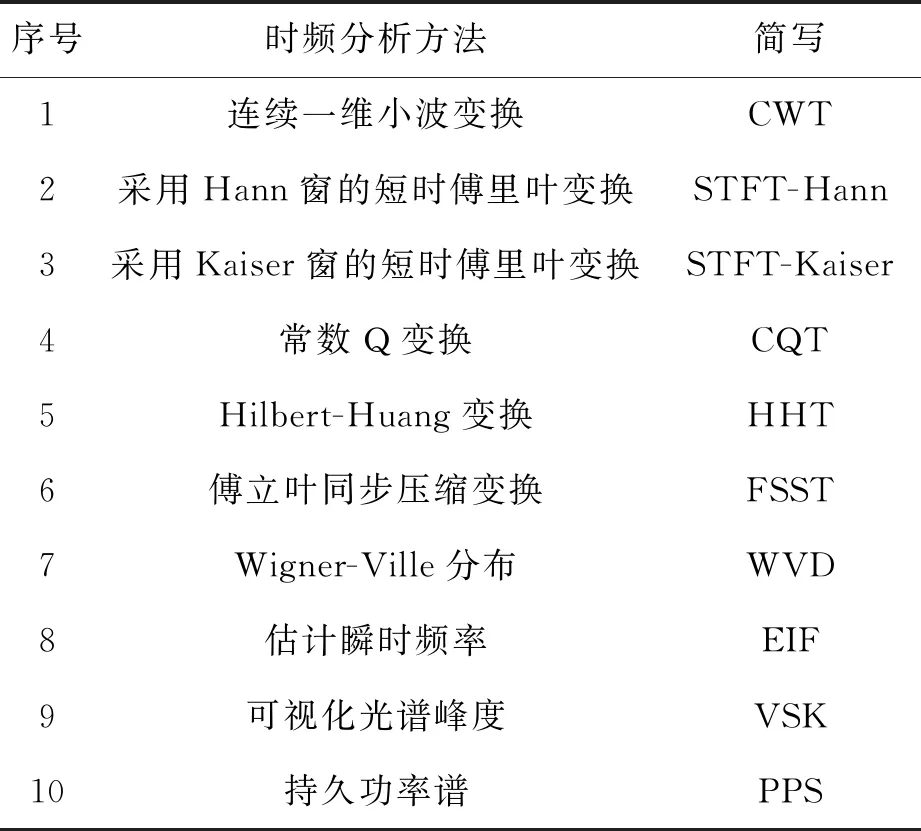
表1 采用的十种时频分析方法

对表1中的10种时频分析方法简要介绍如下。

1) 连续小波变换可以为非周期信号提供最佳分辨结果,而且没有泄露效应。连续小波变换CWT(a,τ)计算公式为

(2)

式中：a为尺度;s(u)为原始信号;τ为平移量;ψ(t)为母小波。

2) 短时傅里叶变换对信号加滑动窗,并对信号做傅里叶变换,得到时变频谱。信号s(u)可以通过指数形式表示为

s(u)=A(u)ejφ(u)

(3)

式中：A(u)、φ(u)分别为信号的幅度和相位。

再通过一阶泰勒公式展开,则信号s(u)转化为

s(u)=A(t)ej(φ(t)+φ′(t)(u-t))

(4)

对s(u)进行短时傅里叶变换,那么有

(5)

式中g(u)为窗函数,本文采用Hann和Kaiser两种窗函数。

将式(4)代入式(5)中得信号的时变频谱为

(6)

3) 常数Q变换在低频处有较好的分辨率[16]。信号的常数Q变换XCQT表达式为

(7)

式中：wNk(n)为长度为Nk的窗函数;Q为CQT变换中的常数因子;k为CQT谱的频率序号。

4) Hilbert-Huang变换共包含两部分:第一部分是经验模态分解(EMD);第二部分是Hilbert谱分析。通过EMD分解,信号s(u)表示为

(8)

式中：N为循环次数;ci(u)为第i个IMF分量;rN(u)为残余分量。再对EDM分解的信号进行Hilbert谱分析,又得

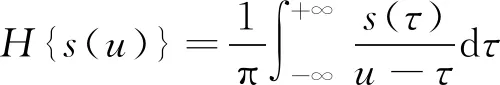
(9)

式中H{s(u)}为信号s(u)的Hilbert变换。

5) 傅里叶同步压缩变换可以获得清晰的频谱估计[17]。信号经过傅里叶同步压缩可表示为

(10)

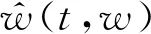
6) Wigner-Ville分布可以提取并跟踪时频脊,对时间和频率具有高分辨率特性,有助于区分相似的调制类型[4]。信号s(u)的Wigner-Ville分布WVDs(u,f)可表示为

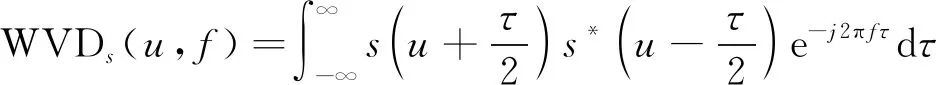
(11)

式中：f为频率;s(u+τ/2)s*(u-τ/2)为信号s(u)的瞬时自相关函数。

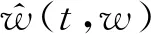
(12)

(13)

8) 可视化光谱峰度是一种4阶频谱分析,表征信号在不同窗口长度下的频域峰度变化[18]。

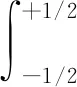
(14)

式中：Zs(f)为正交频谱增量;H(u,f)为信号s(u)在频率f的复数包络。

则信号s(u)的可视化光谱峰度Ks(f)可表示为

(15)

9) 持久功率谱P(ω)可以通过公式(16)提取信号的余晖频谱得到。

(16)

式中：FT(ω)是fT(t)的傅里叶变换,其中fT(t)为功率信号f(t)在时间段t∈[-T/2,T/2]上的表示。

利用上述10种时频分析方法对如图2a)所示的故障信号进行处理,得到对应的不同时频图,如图2b)～图2k)所示。

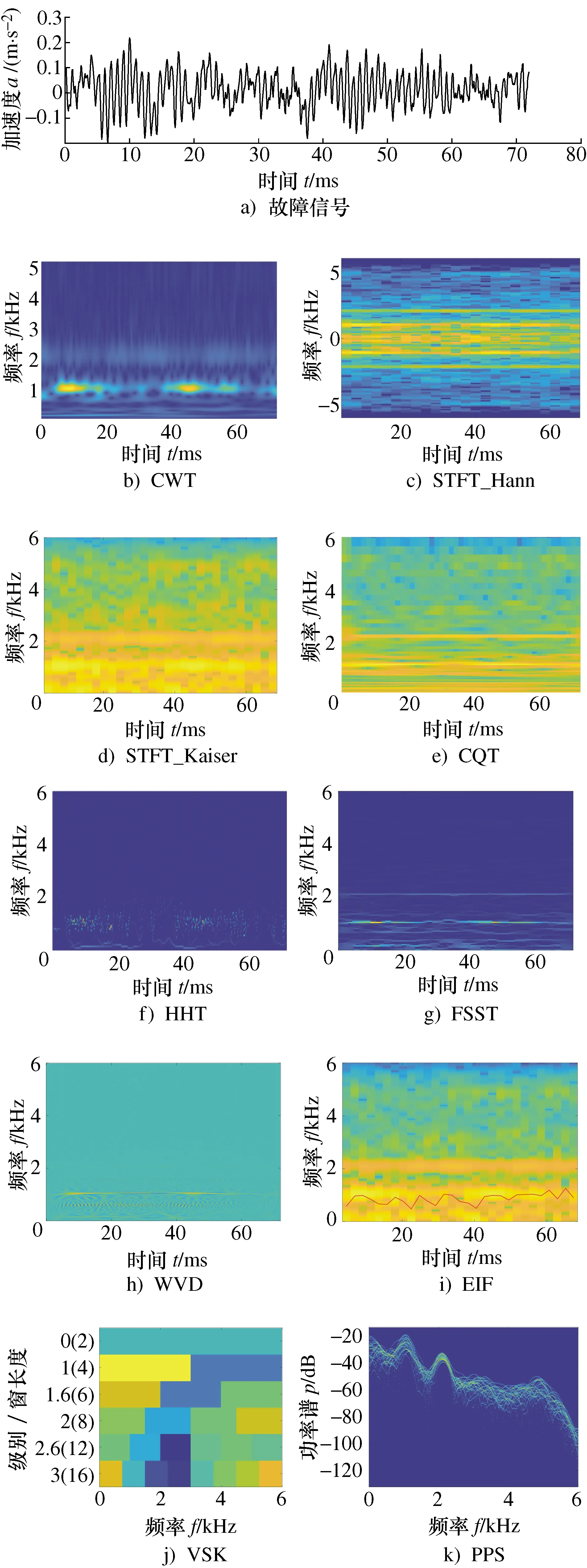
图2 故障信号和对应10种不同时频图

2 滚动轴承诊断模型的构建

2.1 深度卷积神经网络

AlexNet神经网络模型是学者Krizhevsky于2012年提出的一种深度卷积神经网络模型[19]。该模型主要包含5个卷积层和3个全连接层,其中卷积层主要的功能是挖掘二维数据中的深层特征,而全连接层是依据挖掘的深层特征实现数据的分类。该网络的优势在于通过引入ReLU函数、Dropout和数据增强技术减少过拟合。

卷积神经网络的核心组件是卷积层,它可以从输入图像中提取特征。如图3所示,卷积核K从输入图像的左上角开始,每次向右移动1个步幅,卷积核K中的每个参数分别乘以卷积窗口A和B中的参数,将相乘的值相加分别得到8和3,作为下一层的输入。一开始卷积核的参数是随机生成的,并在训练过程中不断更新。

池化层是卷积神经网络的另一核心组件,池化层不仅可以模仿人的视觉对特征图进行降维,简化网络计算的复杂度,而且还能用更高层次的特征表示特征图。在本文使用的AlexNet模型中,采用最大池化,其工作原理如图4所示。池化核从输入层的左上角开始,每次向右移动1个步幅,不同于卷积层的计算方式,池化层直接计算池化窗口A和B的最大值,作为下一层的输入。

图4 最大池化示例

2.2 迁移学习

迁移学习能够将在先前任务中学到的知识和能力应用到新任务中。它的核心思想是从一个或多个源任务中提取特征,从而运用到其它相关的目标任务[20],其原理为

DS={XS,LS},DT={XT,LT},PS≠PT

(17)

式中：DS和DT分别为源模型和目标模型的数据样本;X、L和P分别为数据集、标签和分布情况;下标S和T分别为迁移深度学习中的源域和目标域。

在迁移过程中,预训练模型前n层参数被迁移至新的任务,目标域模型的后m-n层参数使用新任务的数据训练,过程为。

wT(1:m)=[wT(1:n),wT(n:m)]=

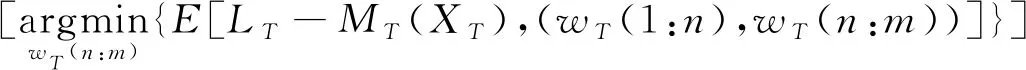
(18)

式中：wT(1:m)为目标域模型的所有权重参数。在目标域模型训练过程中,前n层的全部权重参数wT(1:n)保持不变,后m-n层全部权重参数wT(m:n)根据新数据集训练优化。

2.3 贝叶斯超参数优化

训练神经网络需要指定网络架构和超参数。选择和调整超参数需要大量时间。贝叶斯优化(Bayesian optimization)是一种非常适合分类和回归模型的自适应超参数优化方法[21]。

论文使用贝叶斯优化学习率(Learn rate)、随机梯度下降动量(Momentum)和L2正则化强度3个超参数。目标函数选择训练集的误差率,然后通过测试集数据选择最终模型,以估计模型的泛化误差。其训练时间为2.5 h,优化过程如图5所示。可以看出,函数在计算步数为17时,观测值和估计值相等且最小目标值为0,因此,函数在第17次计算结果最优。此时,3个超参数分别取0.000 1、0.92和0.008 7,使模型达到最优。

图5 贝叶斯参数优化过程

2.4 滚动轴承故障诊断模型

基于不同时频分析的深度迁移学习的滚动轴承故障诊断流程如图6所示。

图6 滚动轴承故障诊断流程

1) 信号采样的原则是保留至少一个转动周期的振动信息,采样长度为

(19)

式中：L为每段信号所包含的采样点数;n为电机转速;fs为采样频率,fs=12 kHz。经计算,L=850。

2) 将步骤1)预处理后的时域数据利用表1中的时频分析处理,得到十种不同的时频图像,采用随机角度旋转、翻转、尺度变换和平移等对图像进行数据增强,然后将信号转化为227×227×3的RGB时频图像数据集。

3) 构建特征迁移模块,加载AlexNet预训练网络,对网络前半部分冻结,后半部分网络进行微调,完成特征迁移模块的构建。

4) 将进一步预处理后的时频图像数据集按照8∶2进行拆分,80%用于训练,20%用于测试,同时添加相应标签,并打乱图像训练集。

5) 将训练集和验证集送入经过微调的网络进行迁移学习训练,同时利用贝叶斯对3个超参数进行优化,进而获得10种不同时频分析的滚动轴承故障模型。

6) 利用步骤5)中得到的滚动轴承故障诊断模型,分别对测试集进行识别,得到轴承的健康状态情况,进而对滚动轴承进行维修或更换。

3 实验验证

本论文使用的滚动轴承实验数据来源于美国凯斯西楚大学(CWRU)电气工程实验室[22],实验对象是SKF6205-2RS深沟球轴承,使用加速度传感器采集滚动轴承不同工作状态下的振动信号,加速度传感器分别安装在电动机壳体的驱动端和风扇端,试验台如图7所示。

图7 轴承故障模拟实验台

实验采用电火花加工技术在滚动轴承的内圈、外圈、滚动体上加工凹坑缺损来模拟故障,分别采集正常、内圈故障、外圈故障和滚动体故障4种状态下的振动信号,如表2所示。Normal表示无故障;IR、Ball和OR分别表示内圈、滚动体故障和外圈故障;0.18、0.36和0.53分别表示每类故障的损伤程度。例如,数据标签IR-18表示损伤程度为0.18 mm的内圈故障。利用加速度传感器分别获得不同故障下的振动信号,其中采样频率为12 kHz,采样总长度为122136。根据由式(1)所示利用重叠采样法,设定单个采样长度L=850,移动步长s=600,可得到200个数据样本数。按照8∶2进行拆分,则训练集有160组,测试集有40组。

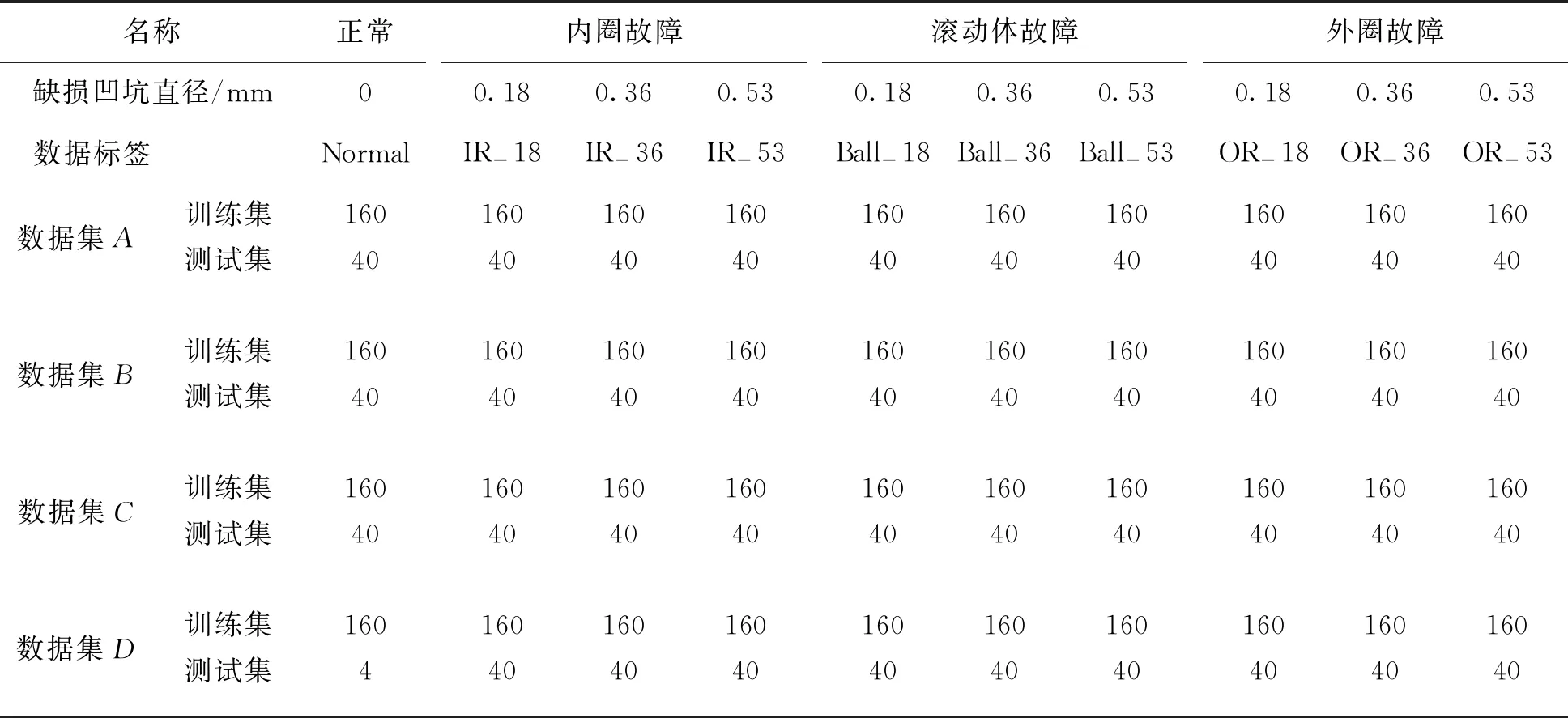
表2 滚动轴承数据集描述

把不同负载下采集的数据分别为用数据集A、B、C和D标记,每类数据集包含训练集和测试集,电机的转速分别为1 797 r/min、1 771 r/min、1 750 r/min和1 730 r/min。其中训练集用来拟合并训练模型,调整超参数以获得最优模型,同时用于模型泛化能力的初步评估;测试集不参与训练模型和调参,仅测试模型的准确率以及评估诊断模型的泛化能力。

3.1 诊断结果对比

为了减轻随机初始值的影响,对每种时频图像进行了5次训练,取其平均值。所使用的计算机硬件,CPU为i5-8400,GPU为NVIDIA GeForce GTX 1050Ti,内存为16GB(DDR4,2 400 MHz)。基于数据集A的10种时频分析和深度学习的滚动轴承诊断结果如表3所示,训练迭代曲线如图8所示。

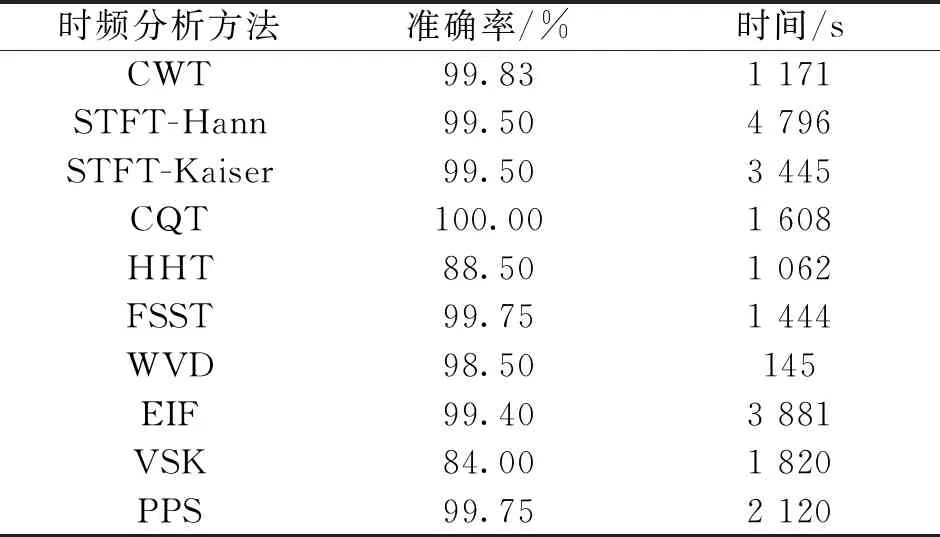
表3 不同时频分析诊断结果

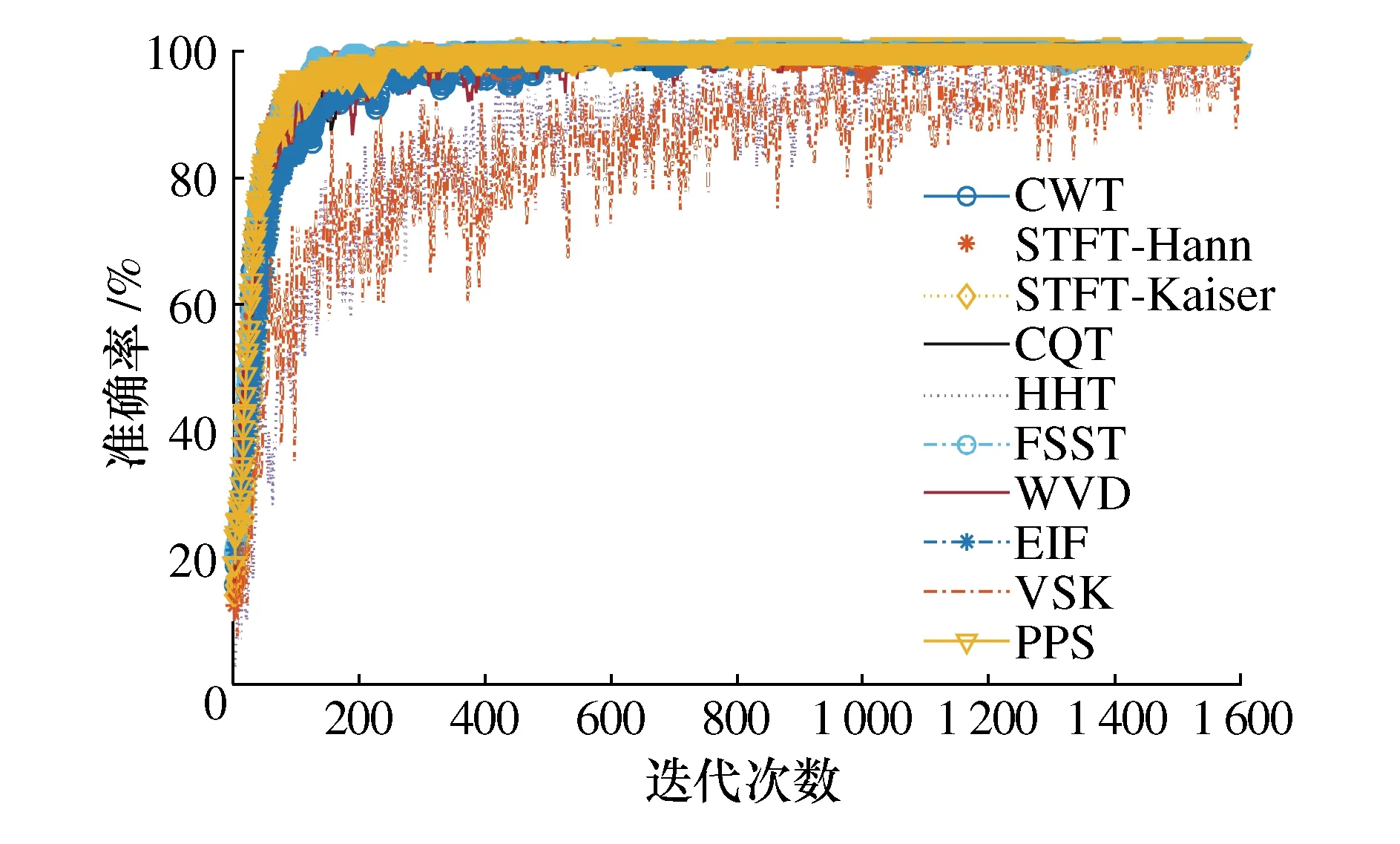
图8 基于不同时频分析的迭代曲线

由表3可知,在10种不同时频分析中,HHT和VSK的准确率在90%以下,其余8种时频分析均能达到98%以上的准确率,其中CQT的准确率为100%。采用两种窗函数的STFT准确率均为99.5%。从训练效率来看,STFT-Hann训练时间最长,为4 796 s,而HHT的训练时间只需1 062 s,但诊断准确率较低,只有88.5%。VSK的准确率也较低,仅有84%。另外可从图8中明显看出,相比于其他时频分析方法,HHT和VSK的训练曲线波动较大,网络学习速度慢,而且需要迭代的次数较多。

通过表3和图8综合来看,CQT的准确率最高,训练时间为1 608 s,所用时长相对较少,同时学习速度也较快。为了进一步评估CQT方法的优势,图9展示了CQT方法训练的过程,横坐标表示训练迭代的次数,左侧纵坐标表示识别准确率;右侧纵坐标表示交叉熵损失,用来量化真实值与模型预测值之间的差异。

图9 CQT训练曲线

从图9可以看出,训练集和测试集的准确率在迭代400次时已经达到100%;交叉熵损失随着迭代次数的增加迅速降低,在迭代400次以后损失值降为0。图10展示了CQT方法的混淆矩阵,横坐标表示预测标签,纵坐标表示真实标签。可以看出,测试集在每个类别上的识别准确率均达到100%,表明基于CQT时频分析和深度学习的滚动轴承诊断模型具有良好的识别精度。因此后面进一步的研究都是利用CQT时频方法和深度学习建立的滚动轴承诊断模型进行的。

图10 CQT混淆矩阵

3.2 样本量对训练结果的影响

为了提高滚动轴承诊断模型的泛化能力,需要大量的训练样本,但是实际工程应用中获取大量真实工况数据样本是不现实的[23],本部分内容重点评估前文所建立的滚动轴承诊断模型对样本数量的依赖性。如表2所示,在本次实验中,分别使用400、600、800、1 000、1 500和2 000个样本数量研究模型的性能,所有的训练样本都是从数据集A中选取的。训练结果如图11所示,当样本数量为400时,模型识别准确率低于90%,随着样本数量的增加,准确率明显提高,训练样本从400个增加到800个时,准确率提高了11%。当样本数量为2 000时,准确率可达100%。表明随着样本数量的增加,诊断模型的泛化能力提高,当样本数量达到2 000时,本文所建立的滚动轴承诊断模型识别准确率就可以达到100%。

图11 不同数量训练样本识别结果

3.3 t-SNE特征可视化

为了直观的理解基于时频分析和深度学习模型逐层提取特征和状态分类的能力,采用t-SNE[24]分别对测试集样本、网络第一个卷积层和Softmax层提取到的特征进行可视化表示,结果如图12所示。

从图12a)可以看出,直接通过原始测试集样本很难对故障进行分类,不同故障完全混淆;图12b)展示当测试样本经过第一个卷积层之后,模型提取到的特征表现出可分性,但是仍有大部分故障难以区分;从图12c)中可以明显看出,经过Softmax分类层后同一类故障被集中地聚集到一起,各种故障被完全分开。这说明基于CQT时频分析和深度学习提取的特征表现出良好的分类性能,可以有效地诊断出滚动轴承的不同故障。

4 不同工作环境下的性能分析

在实际应用中,机械设备的工作状况通常比较复杂。比如:工作负载会根据生产情况不断变化,要收集和标记足够的训练样本以使模型对所有工作负载都具有鲁棒性是不现实的。因此,利用同一工况下收集的样本数据训练故障诊断模型,进而实现类似工况和故障类型的识别是十分有意义的。其次,在实际工作环境中采集的振动信号会夹杂不同程度的噪声,甚至噪声信号强度远大于故障信号强度,导致故障信息淹没在噪声中。所以,诊断模型在不同噪声环境下的诊断能力直接影响着故障识别准确性。基于上述两点原因,本部分重点分析不同负载和噪声情况对所建立的故障诊断模型识别准确性的影响。

4.1 不同负载下的性能分析

测试基于CQT时频分析和深度学习模型在不同负载下的适应性能。将表2中的数据集细划分为源域和目标域数据,具体实验方案设置如表4所示。分别以同一负载下收集的数据集B、C和D单独作为样本来训练诊断模型,然后将其余两个数据集单独作为测试样本来评估模型的准确率。相关结果如图13所示。

表4 针对负载适应性的数据设置

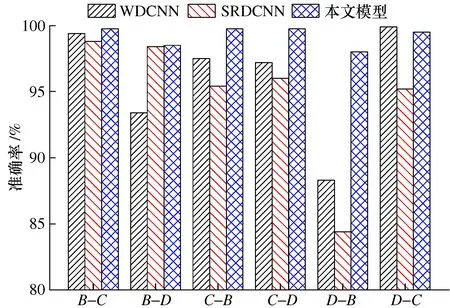
图13 不同负载域下的性能对比

在图13中,柱状图分别为文献[3]、文献[15]以及本文所建立的故障诊断模型在不同负载域下的诊断准确率。B-C表示以数据集B作为源域训练诊断模型,数据集C作为目标域测试模型的准确率。其中文献[3]是利用宽第一层核的深度卷积神经网络(WDCNN),文献[15]是利用堆叠式残差扩散卷积神经网络(SRDCNN),对故障信息进行特征提取。文献[3]和文献[15]方法的平均准确率分别为95.95%和94.7%。当数据集D为源域,数据集B为目标域时,这两种方法准确率均在90%以下。相比之下,基于CQT时频分析的诊断模型相比前两种模型分别提高了9.7%和14.4%,在6个场景中其平均准确率为99.21%。结果表明,基于CQT时频分析和深度学习的故障诊断模型在不同负载下表现出良好的适应性。

4.2 不同噪声下的性能分析

为了评估CQT时频分析和深度学习的故障诊断模型的抗噪性,在原始信号中添加不同程度的高斯白噪声。其中信号和噪声相对强度通过信噪比SNR描述,即

(20)

式中:PS为信号功率;PN为噪声功率。

设置SNR的变化范围为-4 dB～10 dB,间隔为2 dB,从而构造出不同信噪比的数据集。如图14所示,展示数据集A对应的原始信号(将10类信号依次连接)和添加不同噪声生成的8种含噪信号。可以明显看出,当噪声强度较大,如RSN=-4 dB或RSN=-2 dB时,原始信号会被噪声淹没。

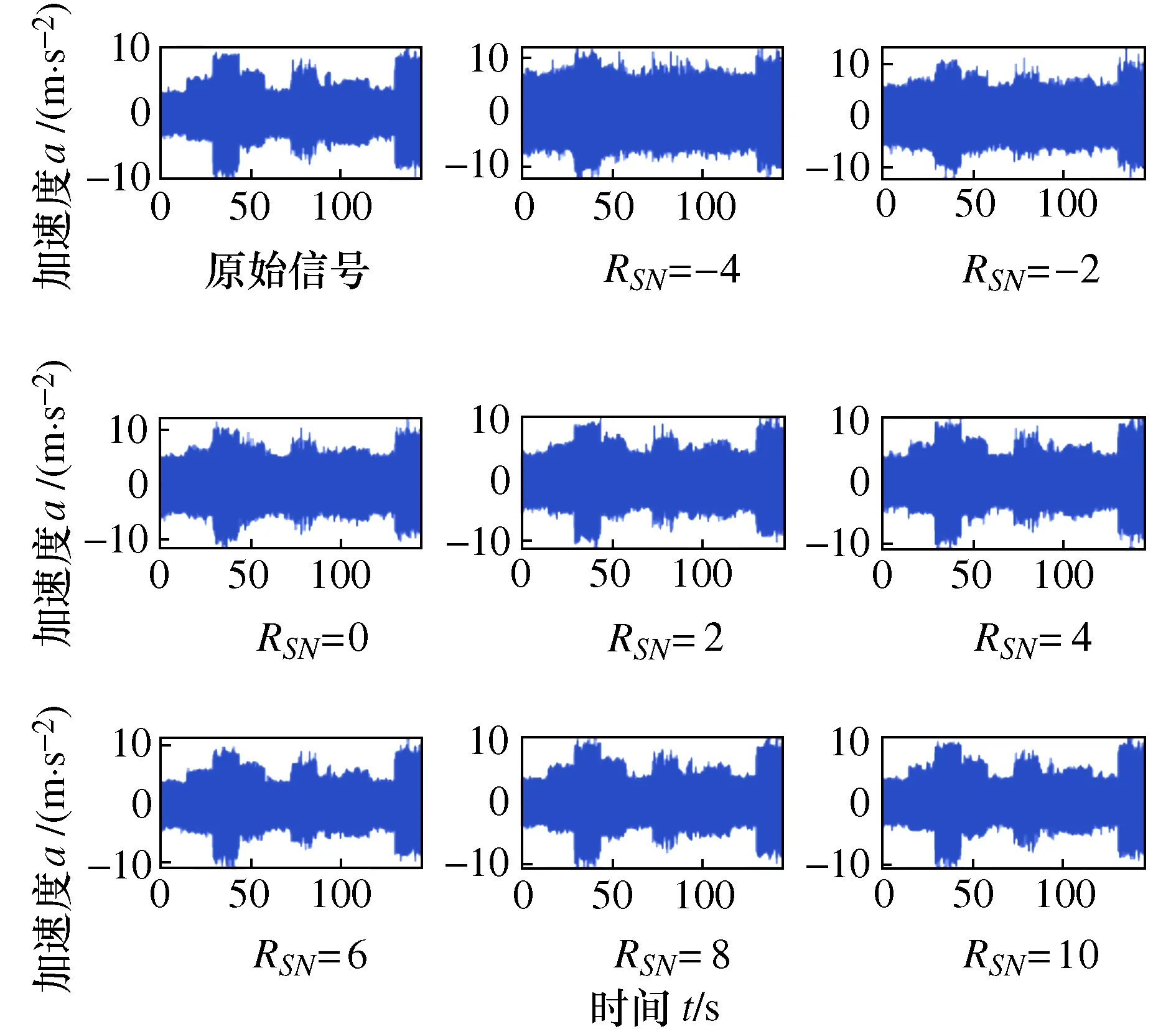
图14 原始信号和加噪信号

图15对比了文献中故障诊断模型WDCNN、SRDCNN和本文建立的故障诊断模型在不同噪声程度下的识别精度。当RSN≥4 dB时,3种模型的准确率均可达到99%以上,当RSN≤0时,可以明显看出本文所建立的故障诊断模型在不同信噪比下的识别准确率均高于两种文献中的模型,当RSN=-2 dB时,WDCNN与SRDCNN诊断模型的识别准确率下降到90%以下,而本文建立的诊断模型识别准确率仍在93%以上。结果表明,3种模型在弱噪声环境下的诊断能力接近,在强噪声环境下,基于CQT时频分析和深度学习的故障诊断模型的抗噪性明显优于其他两种模型。

图15 不同信噪比下的准确率对比

5 结论

论文针对复杂工况条件下滚动轴承故障识别精度不高的问题,开展了一种基于时频分析和深度学习的滚动轴承诊断方法,并通过实验数据验证了所提方法的有效性和鲁棒性,主要结论如下:

1) 对比分析了10种时频分析方法,共有8种时频分析方法能达到98%以上的准确率,其中CQT的诊断精度可达100%。利用CQT得到的时频图作为后续轴承故障诊断模型的输入,无需人工干预故障特征量的提取,实现了轴承故障的自动识别。

2) 建立了基于深度学习的滚动轴承故障诊断模型。在较少训练样本数据情况下,利用迁移学习实现了对不同轴承故障类型的诊断。

3) 通过实验数据,验证了所提方法的有效性和识别精度。通过与文献中的WDCNN和SRDCNN模型比较,在不同负载和噪声强度下,本文所提方法表现出良好的适应能力和抗噪性,从而证明所提方法在不同工作环境条件下都有较好的鲁棒性和较高的识别精度。