面向固定条盒自动装填设备协同设计的任务规划研究

王北海，吴云迪，姚成汉

面向固定条盒自动装填设备协同设计的任务规划研究

王北海，吴云迪，姚成汉

（武汉轻工大学 机械工程学院，武汉 430048）

解决固定条盒自动装填设备的复杂机械设计中，多人协同设计的作业效率问题。采用基于模糊设计结构矩阵（FDSM）的任务规划方法进行任务规划，根据机械设计关联尺度将整体设计任务进行分解，将各设计任务间的耦合关系度量化并构建模糊设计结构矩阵，经过行列变换和分区算法解耦，得出规划后的协同设计任务顺序和分配。通过G–value值验证，优化前后矩阵紧密性程度降低了24.95%了，有效降低了多人协同的相互制约。基于模糊设计结构矩阵（FDSM）的任务规划方法能有效提高固定条盒自动装填设备多人协同设计的工作效率。

协同设计；任务规划；模糊设计结构矩阵；自动装填设备

协同设计是以缩短产品开发周期，改善产品质量和降低成本为目的，同时为团队成员塑造了一种相互协作、相互信任和知识共享的工作观念[1-2]。伴随着数字化、智能化技术的蓬勃发展，协同设计以“互联网+”为前提的条件下，在制造业中得到了有效的发展，良好地解决客户所提出的多样性、灵活性、定制化的需求[3-5]。

目前，协同设计在国内外有着广泛的研究，主要体现在任务分解、流程建模及耦合任务的识别与规划等方面。刘电霆等[6]通过产品原子设计任务之间的模糊性，建立了基于产品众包任务模块划分的优化模型，并利用蚁群算法对其进行分析，得到了其相关执行顺序。Arnarsson等[7]使用设计结构矩阵（DSM）对复杂的产品开发过程进行建模，优化工作流程。金运婷等[8]研究基于流程的模块化开发方法，提出了关于PSS的模糊结构矩阵，并用权重流向图来表示设计任务之间的关系。吴红芳等[9]提出了WBS的FDSM模型，通过对耦合任务的识别和分析，采用割裂算法并结合WBS的权重有向图，结合实例证实了对所提出模型的有效性和通用性。Shekar等[10]利用设计结构矩阵（DSM）管理飞机设计过程中的复杂性，协调不同学科的众多工程师。Cook等[11]将一种增强型遗传算法（GA），用于排序DSM，以优化产品开发中关联活动的进行顺序。刘文林等[12]提出的全局–局部分析方法，详细分析了齿轮传动系统协同设计任务之间的耦合关系，并采用分区算法对其进行解耦后得到设计任务的执行顺序。

固定条盒自动装填设备开发是校企合作项目，设备开发的技术难度大，企业方要求尽量缩短开发周期，占领市场先机。双方决定校企人员混合参与设计项目，并各自在原单位完成设计作业。为了合理确定设计参与人员和任务分配，一种基于模糊设计结构矩阵的全局–局部分析方法，用来深入研究设计任务之间的量化关系，对固定条盒自动装填设备的协同设计进行科学任务规划，以强化人员协同，提高设计效率。

1 协同设计任务的分解与建模

1.1 协同设计任务分解

设备在协同设计开发过程中，由于多个设计人员的共同协作，因此在多个子任务或子过程之间会存在复杂的信息交互、相互依赖和制约的关系。为提高设计开发效率，有效开展协同工作，必须针对设计进行合理的任务规划。任务分解则是制定任务规划的第1步，也是最重要的一步，旨在将设计任务分解成多个子任务，确定其相互关系，方便各个设计人员协同完成设计任务[13]。

协同设计任务的分解见图1，各个设计任务之间存在复杂的耦合关系，在实际设计过程中需要首先完成对设计任务的合理分解组合[14]。

1.2 协同设计任务的设计结构矩阵

设计结构矩阵（Design Structure Matrix, DSM）[15]以矩阵的形式表达复杂设计过程中变量间的信息依赖关系，从中可以迅速发现在执行某一设计任务时，需要哪些信息输入和输出。设计结构矩阵见图2。

通过设计任务信息的输入、输出之间形成的约束的关系，可将结构矩阵分为3种类型，见表1。

对DSM关联矩阵进行分析：关联矩阵的维数表示设计任务的个数，对角线上的元素代表设计任务本身；、表示相关部件的设计任务，数字0、1表示任务间的信息交互，1表示有信息交互，0表示没有信息交互；默认设计任务本身之间存在信息交互，即对角线上的元素都为1；每行的元素表示输入的信息，每列的元素表示输出的信息；对角线以下的元素表示该设计任务对其后相关设计任务所需的输出信息，对角线以上的元素表示所需的输入信息；通过矩阵的变换进行后处理，尽量减少因输入信息所造成的重复设计，因此下三角设计结构矩阵为理想设计规划，意味着该设计任务是没有反馈的串行开发方式。

在实际的机械设备设计过程中，2个设计任务之间存在许多不确定因素，因此传统的布尔值0、1不能良好地表达设计任务之间的关系。文中通过构建模糊设计结构矩阵（FDSM），采用[0，1]之间的数来描绘设计任务之间的模糊关联，使之更加符合实际。

1.3 协同设计任务信息交互的度量化

当识别完设计任务间的信息交互后，需要将其度量化，参考文献中所提供的计算方法得到的数值能良好地描述2个任务间数据输入输出的交互程度，且数值的大小在[0,1]之间，从0至1表示信息交互的程度，越靠近1表示信息交互程度越大，同理越接近0表示信息交互程度越小。

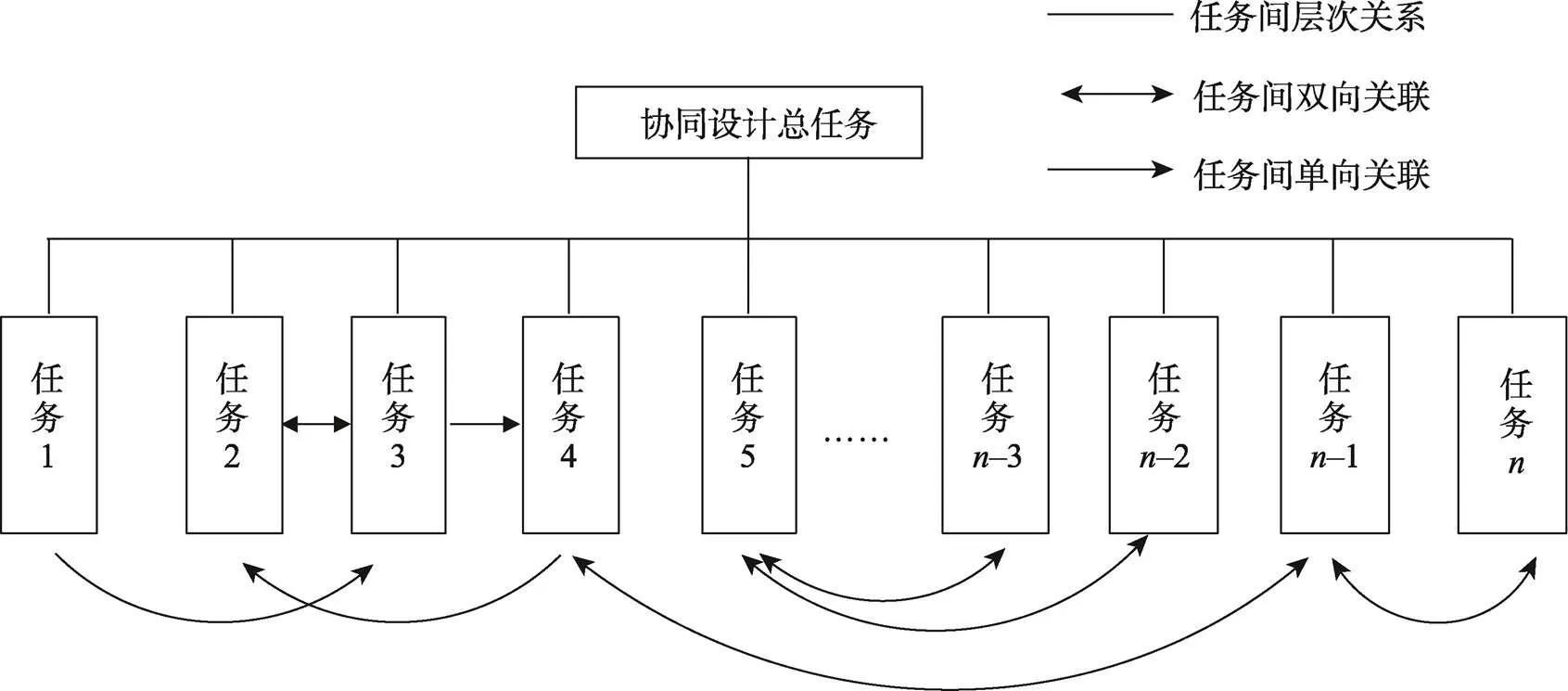
图1 任务分解示意图

图2 设计结构矩阵

表1 3种类型设计结构矩阵

Tab.1 3 types of design structure matrix

用I表示设计任务T输入信息的数量；用O表示设计任务T输出信息的数量；用表示设计任务T输入信息的数量；用O表示设计任务T输出信息的数量；用I∩O表示设计任务T输入信息与T输出信息存在信息交互的数据数量；用I∩O表示设计任务T输入信息与T输出信息存在信息交互的数据数量；则两设计任务之间信息输入和输出之间交互程度的耦合数的计算方法如下：

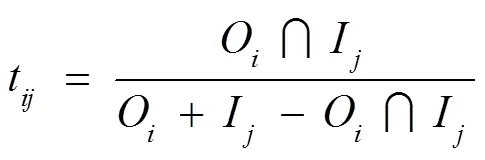
将式（1）和（2）求出的数值赋予2种内涵：表示两设计任务之间信息交互的程度，为方便理解，将两设计任务之间信息交互的程度定义为耦合度；在有向图中表示两设计任务之间的权重。

将式（1）和式（2）求出的数值，采用四舍五入的原则保留一位有效数字，然后将这些数值填入图2中构建模糊设计矩阵。

1.4 协同设计任务的规划流程

以刘文林等[12]提出的基于FDSM的全局–局部两级任务规划方法为基础，提出文中协同设计任务的规划方法，见图3。

2 固定条盒自动装填设备协同设计任务规划

文中以固定条盒自动装填设备为例，根据上文提出的任务规划方法，对其协同设计任务进行分析并得出结论。

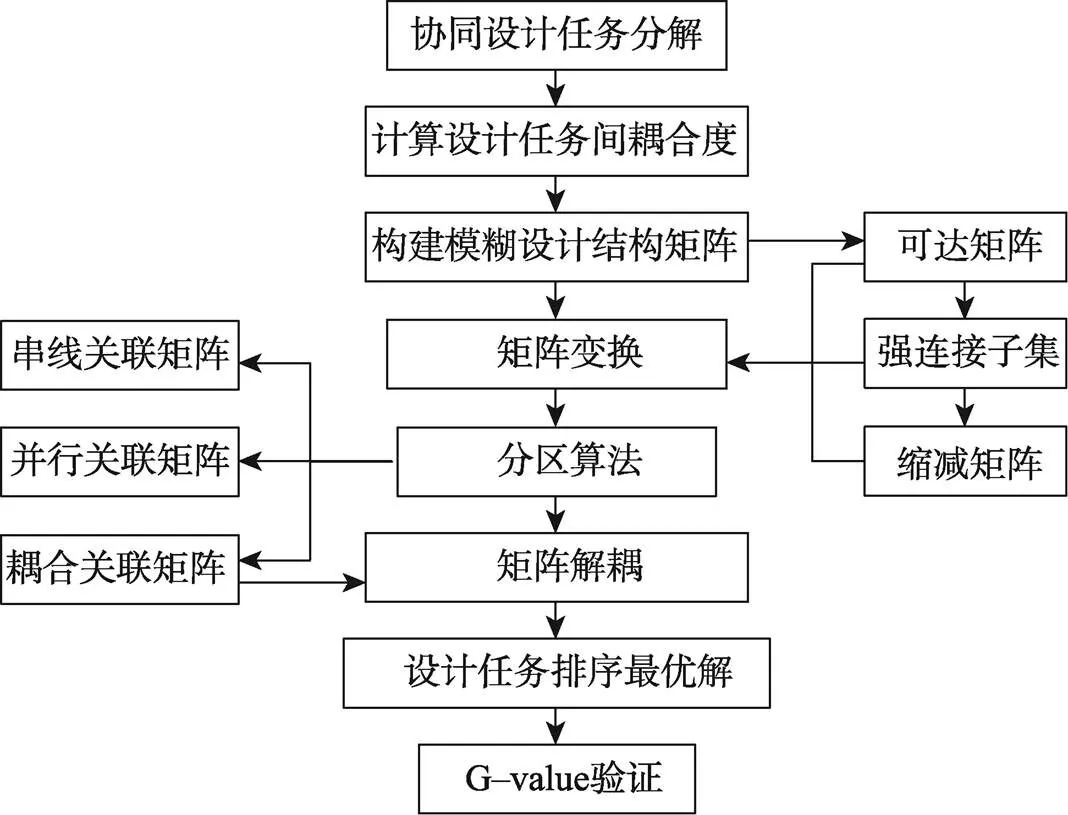
图3 协同设计任务规划

2.1 固定条盒生产线设计任务的分解与建模

2.1.1 功能部件设计与任务分解

根据固定条盒自动装填设备的生产工艺（图4），设备可分解为15个功能部件：AB机架、输送主链、AB输送主链机架、主台面板、干燥剂溜槽、开硫酸纸装置、夹取干燥剂装置、喷码装置、定位装填机构、条盒换道组件、双通道小盒输送装置、线体外罩、收盒输送线、视觉检测组件、收硫酸装置，每个功能部件的设计即为一项可分配设计任务。

2.1.2 设计任务的建模

根据实际调研，以设计任务1和3为例，1={输送主链的尺寸，AB输送主链机架的相对尺寸，干燥剂溜槽的尺寸，气缸的位置，螺纹孔的位置和大小}；1={AB机架的长，AB机架的宽，AB机架的高，AB机架两钢管之间跨度，AB机架的间距，AB机架与输送主链的相关位置}；3={主台面板的尺寸，型钢选材，AB机架与输送主链的相对位置，AB机架两钢管之间跨度，定位装填机构气缸的位置，干燥剂溜槽的尺寸，输送主链的尺寸}；3={AB输送主链机架的相对尺寸，螺纹孔的位置，螺纹孔的大小，气缸的相对位置}。根据式（1）和式（2）可求出各个设计任务之间的耦合度，可得：

由于篇幅限制，其他设计任务间耦合度在此不再赘述。据此求出的耦合度构建如图5所示FDSM和图6所示有向图。

图4 工艺流程图

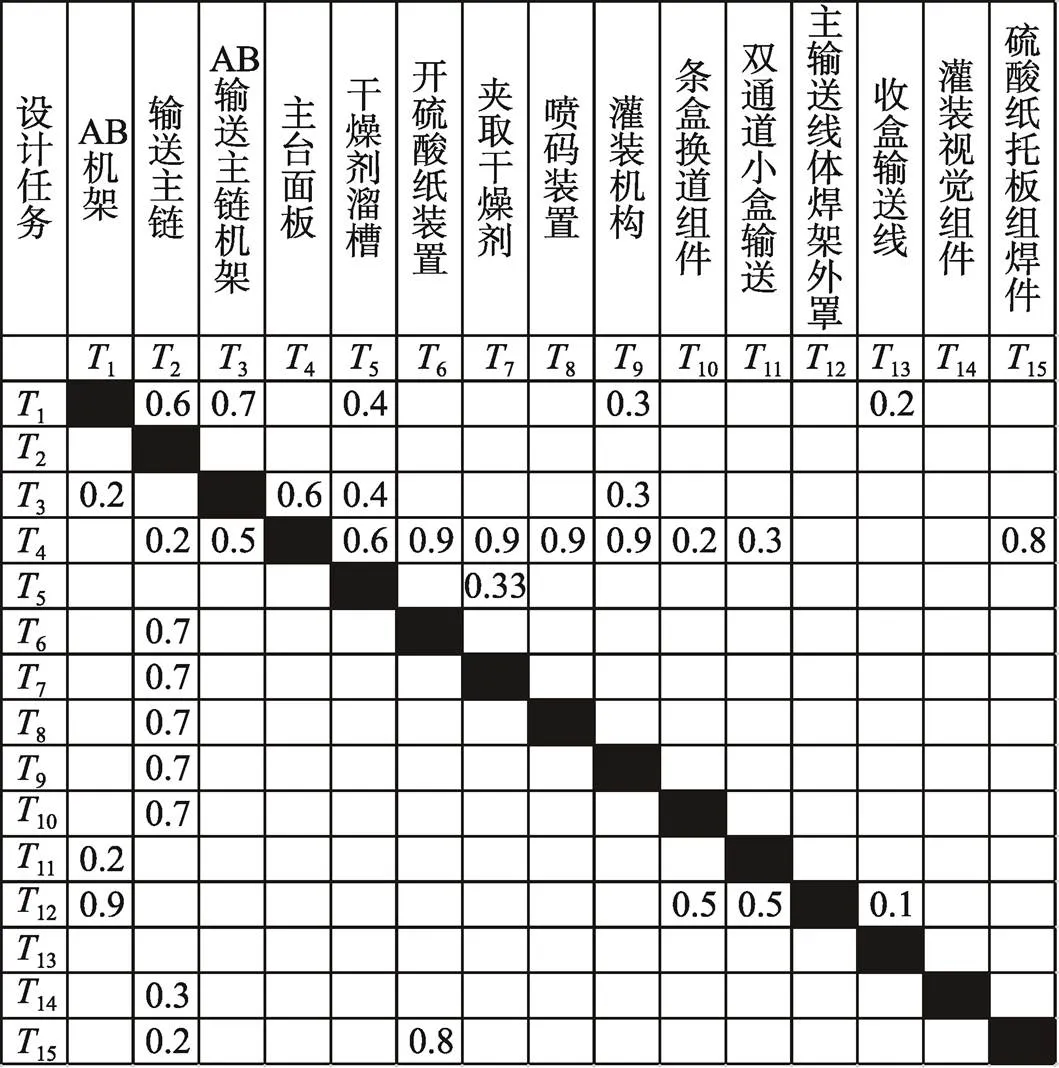
图5 初始FDSM

图6 有向图

2.2 固定条盒生产线设计任务的执行

对上述所求模糊设计结构矩阵进行行列变换，变成下三角矩阵，以减少耦合次数和工序返工次数。下面根据任务规划图逐步进行处理。

2.2.1 FDSM的矩阵变换

在进行矩阵变换时，以初始FDSM为基础，一共有4个步骤。

第1步，求可达矩阵。

可达矩阵是一种0—1矩阵，又称布尔矩阵，它是针对节点矩阵而言，一般把有向图的可达性用可达矩阵表示。它的运算过程基于布尔运算法则，即0+0=0，0+1=1，1+1=1，0×0=0，0×1=1×0=0，1×1=1。在此处，提供2种求可达矩阵的方法：通过有向图可直接求出可达矩阵；先将FDSM变成节点矩阵，然后通过式（3）求出其可达矩阵[16]。本实例的可达矩阵见图7。

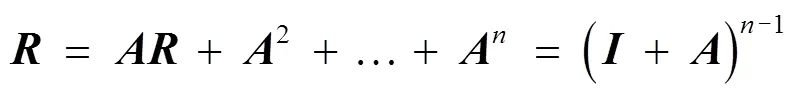
第2步，求强连通子集。

连接矩阵是针对可达矩阵而言，在有向图中存在以下4种关系[17]。

1）T↔T，表示两任务互通，即两设计任务互有信息交互，t=t=1。

2）T× T，表示两任务不互通，即两设计任务无信息交互，t=t=0。

3）T→T，表示T是T的充分条件，t=1，t=0。

4）T←T，表示T是T的充分条件，t=0，t=1。

满足关系1的两设计任务为强连通关系，满足关系2和3的两设计任务称为弱连通关系，满足关系4的设计任务为无连通关系。设T=(1,2,,r)T，r‒维行向量，并将r中互不相等的行向量构成新的集合{1,2, …,r'}，1≤≤。则有：

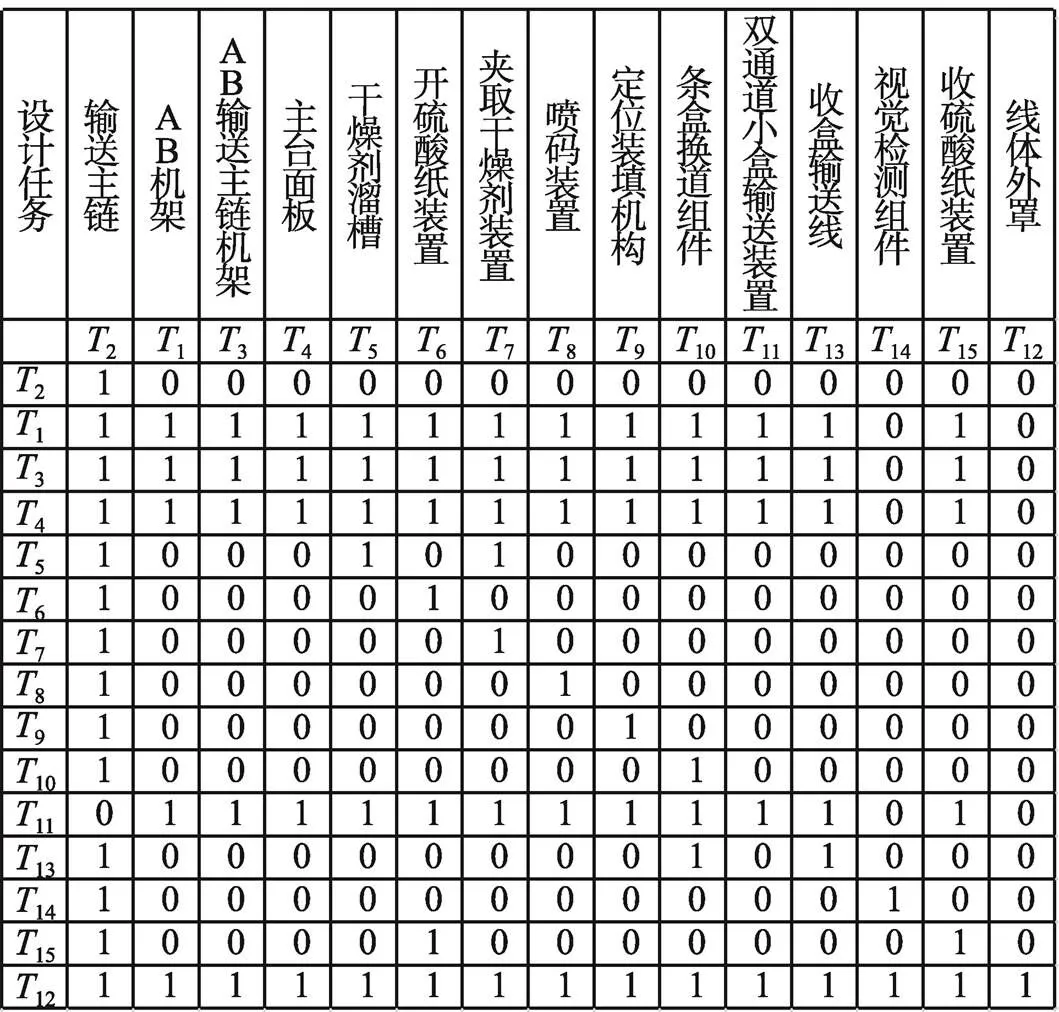
图7 可达矩阵R

1）设（≤）为r'中有一个以上分量值为1的行向量的个数，则表示在协同设计任务中耦合设计任务的数量；

2）设r'中所有值为1的分量是r'1,r'2,,r'，2≤≤，则子系统{r'1, r'2, …,r'}表示一个强连通子集，即协同设计任务耦合集。

据此求出的矩阵T见图8。由此可推出强连通子集为c1={1，3，4，11}。若取11为强连通子集的代表元素，则得到缩减矩阵，见图9。并将图9中的耦合信息进行列汇总，见表2。

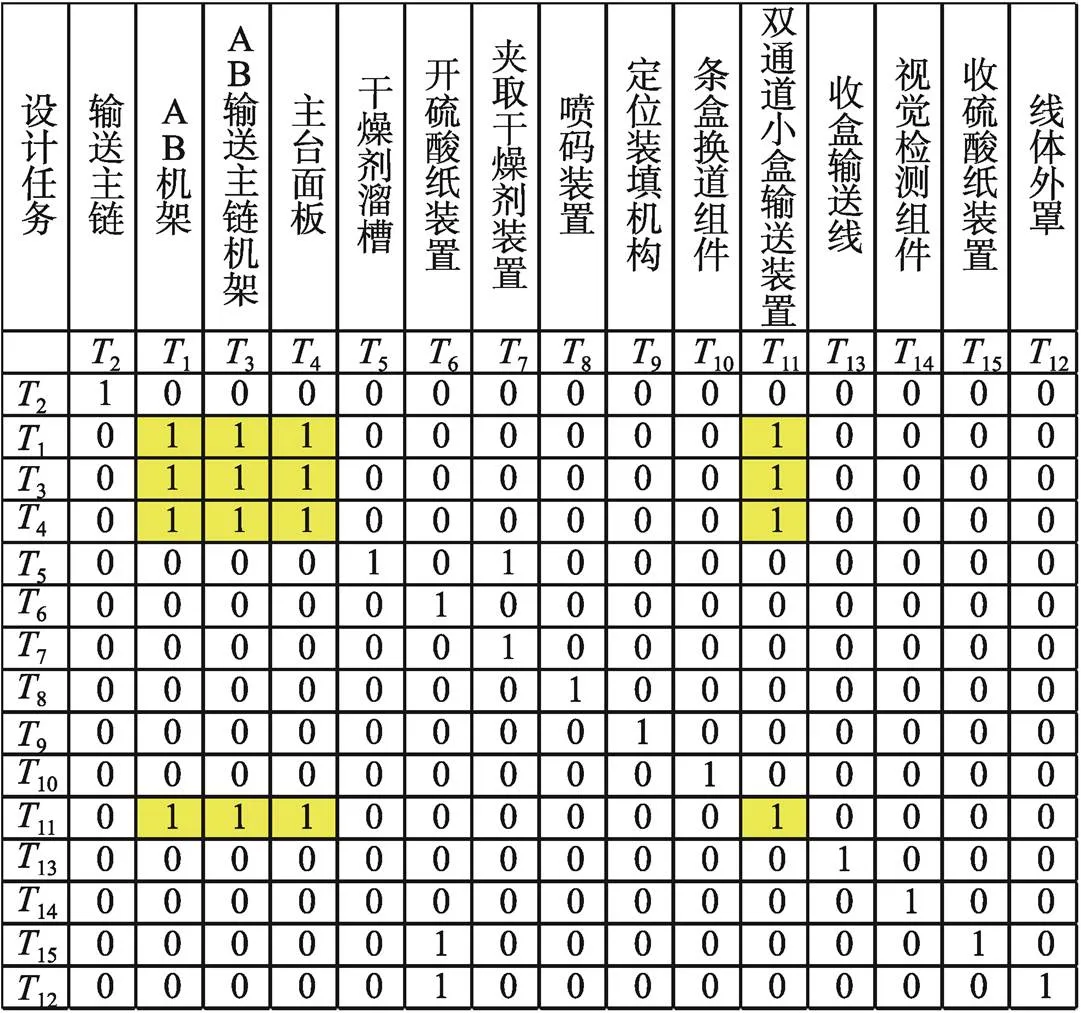
图8 矩阵R∩RT

图9 缩减矩阵

Fig.9 Reduction matrix

表2 行列信息汇总

Tab.2 Summary of row/column information

根据模糊设计结构矩阵的性质，故选取行信息为排序原则，则初步得到设计任务排列：2→6，7，8，9，10，14，15→5，13→c1→12。

2.2.2 矩阵解耦

在有向图中，以两设计任务之间的耦合度作为两者的权重，也可看作两任务之间的距离，因此把耦合任务集中元素从原始FDSM中提出，然后将其进行行列汇总，其行列比表示在信息交互中，输入和输出之间的比重，值越大说明输入占的比重越大，反之输出占的比重越大。相关信息见表3。

表3 耦合子集信息汇总

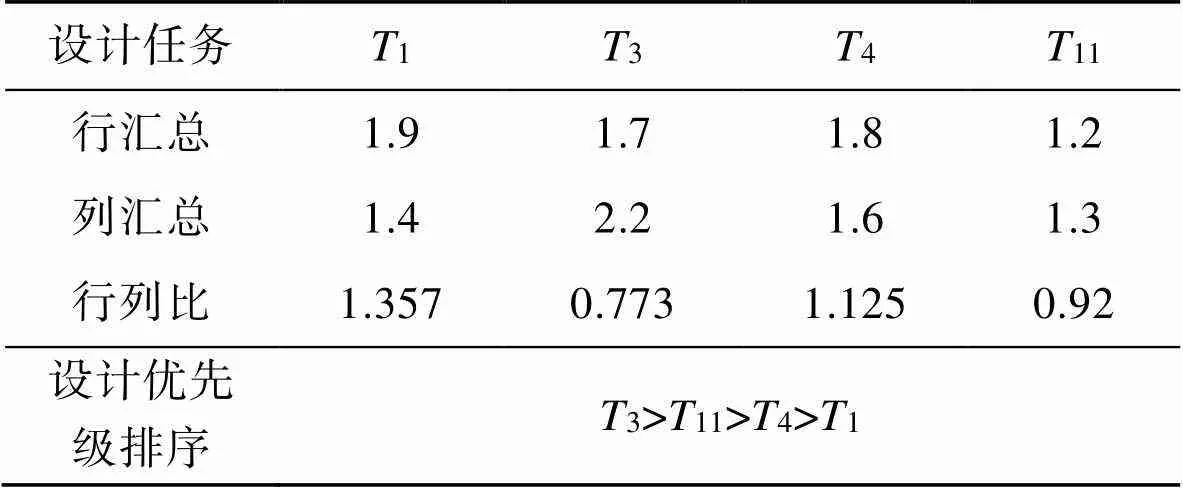
Tab.3 Summary of coupling subset information

结合矩阵变换后得到的设计顺序，则可到总的设计任务顺序为：2→6，7，8，9，10，14，15→5，13→3>11>4>1→12。可将设计任务顺序简化为s1>s2>s3>s4>s5，其中s1={2}、s2={6，7，8，9，10，14，15}、s3={5，13}、s4={c1}、s5={12}。重组后FDSM见图10。

设计任务s1、s2、s3、s4、s5之间存在串联关系，在多人协同设计时，这些设计任务需有一个先后顺序的协同配合；特别地，对于设计任务s2，由于这些任务存在并列关系，因此可任意分配给不同的设计人员同时进行设计；而对于设计任务s4，由于这几个任务之间存在耦合关系，因此在设计时尽可能交于同一人并按照一定的顺序开展设计，避免在人与人进行复杂信息交换时，造成设计误差。

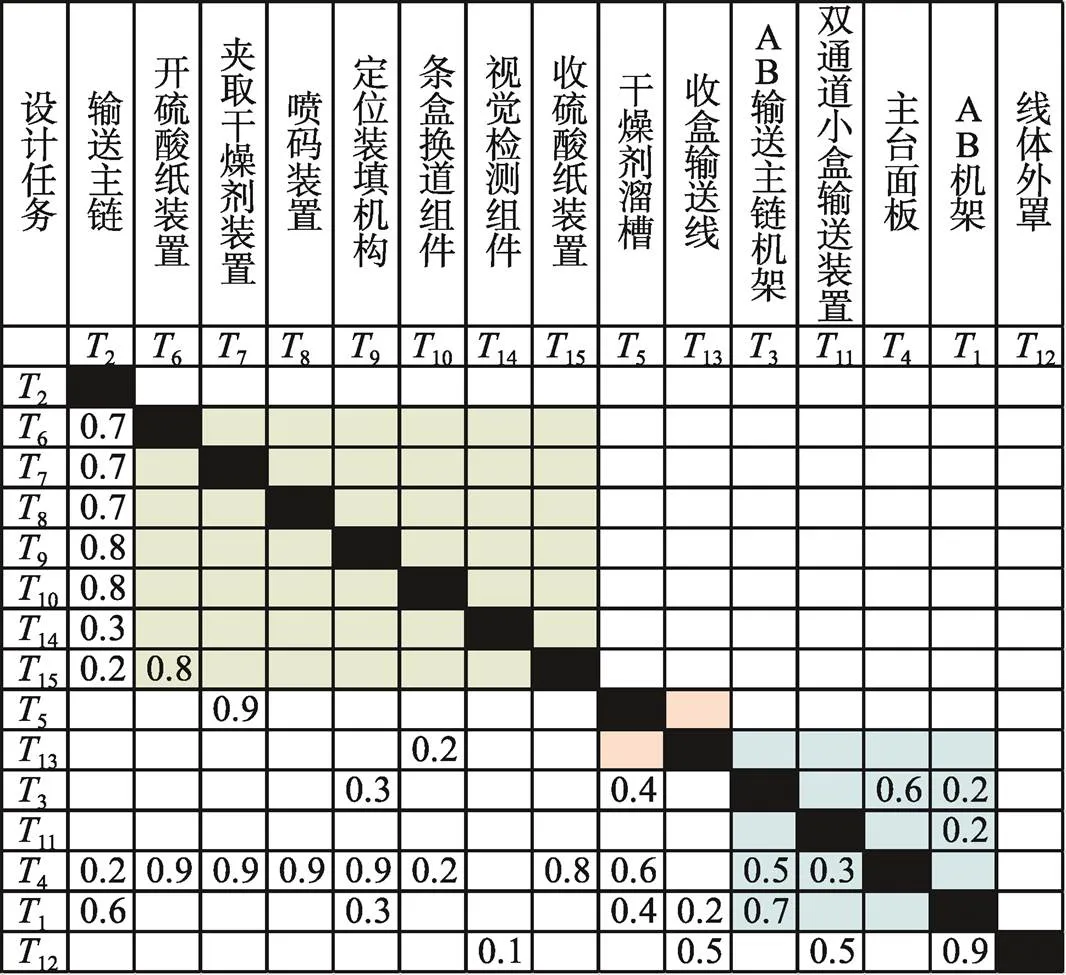
图10 重组后的FDSM

3 规划结果的验证

为验证结果的合理性，根据文献[18]提出G–value的含义：值越大，意味获得的带状对角矩阵具的紧密性越弱，即设计矩阵更加松弛，在协同设计中，设计任务之间关联越松弛，相互制约就越少，不同设计人员之间更容易协同。对模糊设计矩阵进行验证，其表达式为：

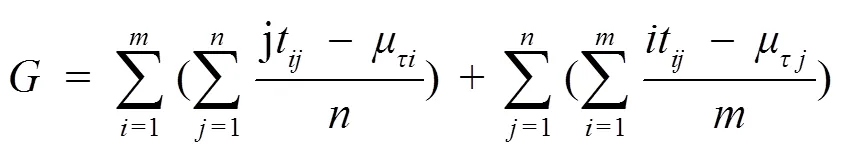
根据式（4）计算得到规划前后FDSM的值分别为202.270 5和252.739 7，优化前后矩阵紧密性程度变化了24.95%。

4 结语

文中面向固定条盒自动装填设备协同设计任务的研究规划，通过分析生产线的各个部分的功能，将整个设计任务分解成多个子任务，为构建模糊设计结构矩阵提供设计基础；通过分析各子设计任务间的耦合关系，并将其度量化，将得到的矩阵进行变换和解耦，得出优化后的设计任务排列顺序和组合关系，为协同设计任务的分配提出参考意见；最后利用G–value值验证了结果的合理性。

在固定条盒自动装填设备的校企开发中，按本研究进行了任务划分和设计作业，重复工作和协调时间大幅减少，实际设计周期比原计划缩短了15 d，节约用时20%。通过文中的研究，不仅减少设备设计任务的返工和迭代次数，提高了设计效率、降低了设计成本，也为后续加工及安装调试作业计划提供了有益参考。

[1] 彭巍, 胡远航, 龚壮辉. 生态视角的复杂产品协同设计网络稳定性研究[J/OL]. 复杂系统与复杂性科学: 1-9[2022-11-19]. http://kns.cnki.net/kcms/detail/37.1402. N.20220414.1911.003.html

PENG wei, HU Yuan-hang, GONG Zhuang-hui. Research on the Stability of Complex Product Collaborative Design Network from the Ecological Perspective[J/OL]. Complex Systems and Complexity Science: 1-9[2022-11-19]. http://kns.cnki.net/kcms/detail/37.1402. N.20220414.1911.003.html

[2] LIANG X D, ZHOU W T, LIU A J, et al. Collaborative Product Design for Tasks Sorting Based on Shortest Delivery[J]. Scientific Programming, 2016(2): 1-6.

[3] 邵天巍, 魏巍, 张瑜, 等. 协同设计驱动的产品创新设计发展[J]. 机械设计, 2019, 36(6): 1-6.

SHAO Tian-wei, WEI Wei, ZHANG Yu, et al. Collaborative Design-Driven Product Innovation Design Development [J]. Journal of Machine Design, 2019, 36(6): 1-6.

[4] KANG X , KANG J , CHEN W . Conceptualization and Research Progress on Web-Based Product Co-Design[J]. Informatics, 2020, 7(3):30.

[5] COLLAZOS C A, GUERRERO L A, PINO J A, et al. A Method for Evaluating Computer-Supported Collaborative Learning Processes[J]. International Journal of Computer Applications in Technology, 2004, 19(3/4): 151-161.

[6] 刘电霆, 胡浩平, 吴丹玲. 社会化产品开发众包设计任务间加权网络建模与模块划分[J]. 工业工程, 2021, 24(5): 95-100.

LIU Dian-ting, HU Hao-ping, WU Dan-ling. Weighted Network Modeling and Module Partitioning among Crowdsourcing Design Tasks for Social Product Development[J]. Industrial Engineering Journal, 2021, 24(5): 95-100.

[7] ARNARSSON V, GUSTAVSSON E, JIRSTRAND M, et al. Modeling Industrial Engineering Change Processes Using the Design Structure Matrix for Sequence Analysis: a Comparison of Multiple Projects[J]. Design Science, 2020(6): 1-6.

[8] 金运婷, 耿秀丽. 基于模糊DSM的产品服务系统流程模块化设计[J]. 工业工程与管理, 2020, 25(2): 155-163.

JIN Yun-ting, GENG Xiu-li. Process Modularization Design of Product-Service System Based on Fuzzy DSM[J]. Industrial Engineering and Management, 2020, 25(2): 155-163.

[9] 吴红芳, 任南, 马梦园. 基于FDSM模型的WBS任务耦合问题的研究[J]. 上海管理科学, 2016, 38(6): 76-79.

WU Hong-fang, REN Nan, MA Meng-yuan. Research on the Coupling Problem of WBS Tasks Based on FDSM Model[J]. Shanghai Management Science, 2016, 38(6): 76-79.

[10] SHEKAR B, VENKATARAM R, SATISH B M. Managing Complexity in Aircraft Design Using Design Structure Matrix[J]. Concurrent Engineering, 2011, 19(4): 283-294.

[11] COOK I, COATES G. Optimising the Time-Based Design Structure Matrix Using a Divide and Hybridise Algorithm[J]. Journal of Engineering Design, 2016, 27(4/5/6): 306-332.

[12] 刘文林, 马雅丽, 李胜甲, 等. 面向齿轮传动系统协同设计的任务规划方法研究[J]. 机电工程, 2021, 38(9): 1132-1137.

LIU Wen-lin, MA Ya-li, LI Sheng-jia, et al. Task Planning Algorithm for Collaborative Design of Gear Transmission System[J]. Mechanical & Electrical Engineering, 2021, 38(9): 1132-1137.

[13] 罗建强, 马光秀, 杨子超. 面向混合产品生成的项目任务分解方法及其应用[J]. 工业工程与管理, 2021, 26(6): 18-26.

LUO Jian-qiang, MA Guang-xiu, YANG Zi-chao. Project Task Decomposition Method for Hybrid Offerings Generation and Its Application[J]. Industrial Engineering and Management, 2021, 26(6): 18-26.

[14] PARK S O, YOON J, AN H, et al. Integration of Axiomatic Design and Design Structure Matrix for the Modular Design of Automobile Parts[J]. Proceedings of the Institution of Mechanical Engineers, Part B: Journal of Engineering Manufacture, 2022, 236(3): 296-306.

[15] BROWNING T R. Applying the Design Structure Matrix to System Decomposition and Integration Problems: a Review and New Directions[J]. IEEE Transactions on Engineering Management. 2001. 48(3): 292-306.

[16] 冯海亮, 亓洪胜. 基于Warshall算法的可达矩阵的算法改进及Python程序实现[J]. 信息记录材料, 2019, 20(8): 74-75.

FENG Hai-liang, QI Hong-sheng. Algorithm Improvement of Reachability Matrix Based on Warshall Algorithm and Python Program Implementation[J]. Information Recording Materials, 2019, 20(8): 74-75.

[17] 李慧, 欧阳鑫玉. 基于动态图的复杂系统建模方法[J]. 计算机时代, 2019(8): 49-52.

LI Hui, OUYANG Xin-yu. A Method for Modeling of Complex Systems Based on Dynamic Graphs[J]. Computer Era, 2019(8): 49-52.

[18] CHEN Li, DING Zhen-dong, LI Simon. a Formal Two-Phase Method for Decomposition of Complex Design Problems[J]. Journal of Mechanical Design, 2005, 127(3): 184-195.

Task Planning for Collaborative Design of Fixed Strip Box Automatic Filling Equipment

WANG Bei-hai, WU Yun-di, YAO Cheng-han

(School of Mechanical Engineering, Wuhan Polytechnic University, Wuhan 430048, China)

The work aims to solve the problem on operation efficiency of multi-person collaborative design in complex mechanical design of fixed strip box automatic filling equipment. The task planning method based on fuzzy design structure matrix (FDSM) was adopted for task planning. The overall design task was decomposed according to the mechanical correlation scale. The coupling relationship between design task was quantified, and the fuzzy design structure matrix was constructed. The fuzzy design structure matrix was transformed into rows and columns, and the partition algorithm was used to decouple. Then the planned collaborative design task sequence and allocation were obtained. The validity of the planning results was verified by g-value, which showed that the compactness of the matrix before and after optimization has been reduced by about 24.95%, effectively reducing the mutual restriction of multi-person collaboration. It is concluded that the task planning method based on fuzzy design structure matrix (FDSM) can effectively improve the work efficiency of multi-person collaborative design of fixed strip box automatic filling equipment.

collaborative design; task planning; fuzzy design structure matrix; automatic filling equipment

TB486

A

1001-3563(2023)03-0172-07

10.19554/j.cnki.1001-3563.2023.03.021

2022–07–18

2019湖北省技术创新专项（重点项目）（2019AFB669）

王北海（1977—），男，博士，副教授，主要研究方向为智能包装装备。

责任编辑：曾钰婵