巧用画图策略 助力难点突破

杨燕华

难点一：以图辨析，明确概念本质

平行线的定义中含有三要素：①在同一平面内；②不相交；③两条直线。对平行线的概念，我们可以分三个方面进行解读：第一层次，不能忽略或丢掉“同一平面内”这个前提条件，否则不一定是平行线；第二层次，平行线是指两条直线，而不是两条射线或线段；第三层次，线段和射线平行都是指线段或射线所在的直线平行。

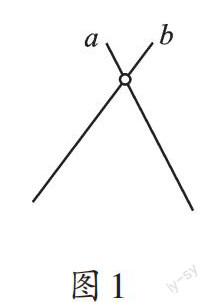
案例1 图1—图3中的两条直线平行吗？

【解析】图1—图3中的两条直线都不平行。平行线的概念比较抽象，有些同学不理解概念，不妨借助圖形明确概念本质。

难点二：以图助析，理清性质要点

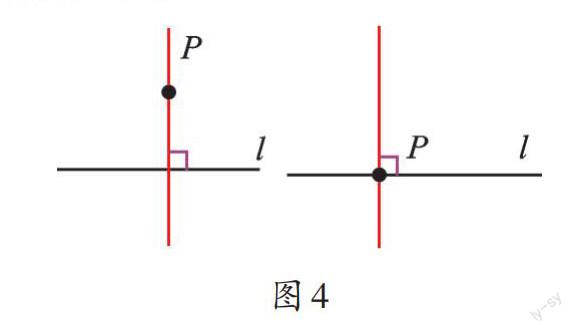
学习垂线的性质，要与平行线的性质前后关联。垂线的性质1说明了垂线的唯一性，即过一点“有”且“只有”一条直线与已知直线垂直，并且这一点具有任意性。注意，“任意一点”有两种可能：一是点在直线外，二是点在直线上（如图4）。这与平行线的性质中“必须过直线外一点”有区别，同学们在解有关问题时要特别注意。

垂线的性质2指出垂线段最短。从直线外一点向直线作垂线，这一点与垂足之间的线段叫作垂线段，这一点与直线上其他各点之间的线段都可以叫斜线段。根据性质1，垂线段是唯一的，而斜线段可以有无数条，并且垂线段的长度总是小于斜线段的长度。

如图5，直线l外一点P与直线l上的点连接所成的线段中，因为PC⊥l，所以线段PC比PA、PB、PD都短。

案例2 铁路l旁有一座村庄A，现要建一个火车站，为了使村庄人乘火车方便，请你选址建火车站，并说明理由。

【解析】乘车最方便，也就是要求距离最近，而根据垂线段最短，则过点A作垂线段即可。

难点三：以图为媒，指明画图方法

1.平行线的画法

在小学，同学们就学过画平行线的方法：①平移三角板画平行线；②利用网格线画平行线。在网格纸上，所有横线互相平行，所有竖线也互相平行，我们也可沿着网格的对角线斜着画，如：斜线段AB是a×b长方形的对角线，所以平移后的线段也是a×b长方形的对角线。画平行线的依据就是图形的平移。

2.垂线的画法

根据垂直的定义可知，画垂线也就是作直角。因为直角的两条边所在的直线是垂直的，所以，垂线的画法通常有三种：①利用三角板的两条直角边或刻度线与所在边的垂直关系，基本步骤是：一靠、二过、三画；②利用量角器画，主要通过画一个90°的角来得到垂线；③利用网格线来画，如：以线段AB为对角线的a×b长方形绕着某一点逆时针旋转90°后得到的b×a长方形的对角线即是符合要求的图形。

案例3 请利用网格画线，过点C画AB的平行线，过点B画AB的垂线。

【解析】如图7，画平行线和垂线的本质就是图形的运动变换。

难点四：以图为引，探索操作类题目

同一平面内两条直线的位置关系，要么是平行，要么是相交。要研究交点的问题，同学们可以借助画图的方法，在操作中加以体验和理解。

案例4 同一平面内的两条直线，平行没有交点，如果相交，只有一个公共点。在同一平面内，三条直线公共点的个数可以是____________。四条呢？在同一平面内，n条直线最多有多少个交点呢？

【解析】同一平面内，三条直线的交点个数可以是0、1、2、3，如图8。

四条直线的交点个数可以是0、1、3、4、5、6。

n条直线的交点个数最多是1+2+3+…+（n-1）=[n（n-1）2]。

变式：1条直线可以把一个平面分成二部分，2条直线可以把一个平面分成三部分或四部分；那么，3条直线可以把平面分成几部分呢？4条呢？

同学们，画图时要注意图形位置的各种可能性，不能想当然，不能想怎么画就怎么画，解题时既要做到心中有数，更要做到心中有图。

（作者单位：江苏省无锡市新城中学）