“展开与折叠”主题进阶学习

孙媛媛

一、“展开与折叠”进阶学习之正方体

例1 在学习“展开与折叠”后，小红想利用相关知识来制作一个无盖的正方体纸盒。

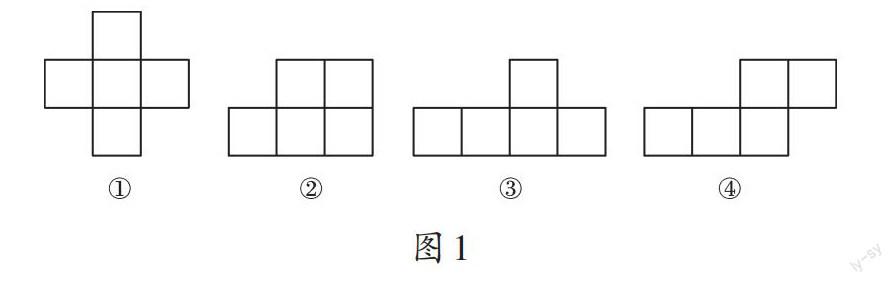
（1）图1中哪个图形经过折叠可以围成无盖的正方体纸盒？

（2）在将纸盒制作好后，小红给其中两个面画上了标记并开口向上放置，如图2所示，若小亮将这个盒子重新展开，请画出其中一种展开图。

（3）假设正方体的边长为4dm，如果小红想在无盖纸盒内部贴满贴纸以便将其改装为收纳盒，则需要的贴纸面积至少是多少dm2？

【解析】（1）①③④可以。我们可以从立体实物出发，辨别给定图形能否折叠成立体图形。如果相邻两条边粘贴成高，需要相邻两边的夹角成九十度。

（2）把立体图形展开时，可以剪取不同的棱，所以展开图有多种类型，比如“1—4型”（图3），“3—2型”（图4）等。答案不唯一。

（3）要求正方体的内部面积，关键要先求出1个面的面积。1个面是16dm2，5个面就是80dm2。

二、“展开与折叠”进阶学习之长方体

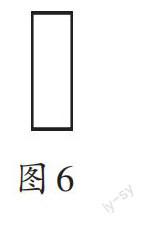
例2 小明将一个长方体沿某些棱剪开，展开成平面图形时，不小心多剪了一条棱，把一个长方体纸盒剪成了图5、图6两部分。

（1）小明总共剪开了几条棱？

（2）小明想将剪断的图6重新粘贴到图5上，再折叠成一个长方体纸盒。有几种粘贴方法？

（3）求长方体纸盒的体积。

【解析】本题考查几何体的展开图，解题关键是掌握几何体的展开图特征。我们运用逆向思维可发现，长方体共有12条棱，去掉4条未剪开的棱，剩下的就是剪开的棱的条数。

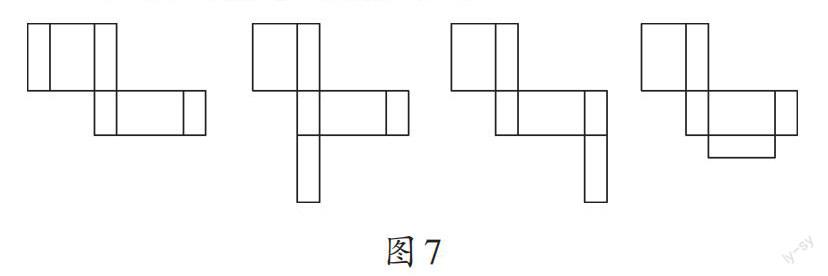
（2）根据长方形边长关系，以及“相等长度的边并排放，相同图形要间隔一个图形”的规则，可以得出4种情况（图7）。

（3）用未知数表示长、宽、高，设高为xcm，则宽为（6-x），利用长相等列出方程10-（6-x）=12-6，解得x=2，则长方体体积为6×4×2=48。

三、“展开与折叠”进阶学习之棱柱

例3 如图8，四个几何体分别是三棱柱、四棱柱、五棱柱和六棱柱，说说他们各有几个面、几条棱、几个顶点？由此猜想n棱柱的面、棱、顶点各有多少？

【解析】我们可以归纳棱柱特征的一般规律：n条棱对应n个面，再加上、下底面，共有n+2个面；侧面上有n条棱，上、下底面都是n边形，共有3n条棱；上、下底面都是相同的n邊形，共有2n个顶点。

四、“展开与折叠”进阶学习之棱锥

例4 如图9，D、E、F分别是等边△ABC的边AB、AC、BC的中点，现沿着虚线折起，使A、B、C三点重合，重合后统一记为M点。（1）折起后得到的空间图形是____________。

（2）将折叠的立体图形沿着棱ME、MF、DF剪开展成平面图，尝试画一画展开图。

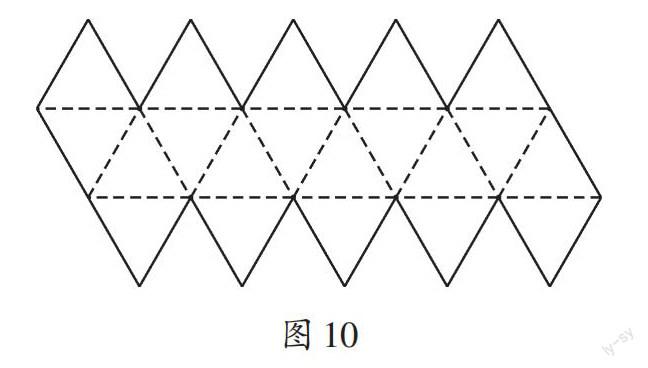
（3）如图10，由20个一样的等边三角形折叠得到的空间图形是____________。

【解析】（1）三棱锥。（2）从立体图形到平面二维图形，我们可以动手剪一剪。（3）由20个等边三角形可以拼成正二十面体。它是由20个等边三角形所组成的正多面体，也是柏拉图多面体之一。医学上，某些病毒如人类疱疹病毒的衣壳就是正二十面体结构。可见，数学是一门基础性工具学科，我们只有现在打好基础，才能在其他学科研究中有长远发展。

（作者单位：江苏省连云港市凤凰学校）