基于组合优化策略的动车组悬挂参数优化设计

张昕磊，李永华，王 衍，李继康

(1.大连交通大学机车车辆工程学院，辽宁 大连 116028；2.大连交通大学计算机与通信工程学院，辽宁 大连 116028)

0 引言

随着动车组运行速度的日益提高，车辆的平稳性和稳定性越来越受到关注[1]。动车组转向架悬挂系统是复杂多参数系统，由于加工制造误差和橡胶老化等原因，使得生产和运行过程中悬挂参数存在不确定性，同时悬挂参数变化影响着车辆运行平稳性和稳定性。因此，分析悬挂参数对动力学性能的影响极为重要。

近年来，国内外学者围绕转向架悬挂参数的优化开展了大量研究。张涛等[2]研究了地铁一系悬挂和扣件刚度参数对车辆动力学性能的影响；王欢声等[3]针对变轨距转向架悬挂参数进行优化匹配，提出了关键悬挂参数匹配方案；岳鹏等[4]基于UM软件建立某高速客车动力学模型，研究了车辆通过曲线时一系悬挂纵向和横向刚度对车辆动力学性能的影响；宗聪聪等[5]利用遗传算法对二系悬挂进行优化，降低了转向架蛇行模态对车体晃动的影响。然而，上述研究需要多次调用非线性程度较高的车辆系统动力学模型，求解参数过程耗时较长，而代理模型利用函数代替复杂的理论模型，能够提高求解效率。Yang等[6]运用Kriging代理模型，通过多岛遗传算法寻求悬挂参数的最优组合。智能优化算法虽然全局搜索能力很强，但是局部搜索能力较差，求解时间长，效率降低[7]。

本文以国内某动车组为对象，使用SIMPACK软件建立车辆系统动力学模型，借助SIMPACK软件与Isight软件联合仿真计算平台分析悬挂参数对横向平稳性的影响，选取5个灵敏度较大的悬挂参数作为设计变量，并以横向平稳性为目标函数建立Kriging代理模型。基于自适应模拟退火算法和非线性序列二次规划算法的组合优化策略，在Kriging代理模型的基础上对悬挂参数进行优化，并通过仿真验证优化结果的有效性。

1 车辆系统动力学模型的建立

根据多体动力学理论，运用SIMPACK软件建立国内某动车组动力学模型，该模型由1个车体、2个构架、4个轮对和8个轴箱组成，轮对与构架通过一系悬挂系统连接，构架与车体通过二系悬挂系统连接，其拓扑结构如图1所示。

图1 车辆系统动力学模型拓扑结构

参考TB 10621—2014《高速铁路设计规范》进行仿真运行工况设置，直线和曲线工况行驶速度均为300 km/h，直线工况运行里程为1 500 m；曲线共有3种工况，曲线线路参数设置为：直线、缓和曲线和圆曲线长度分别为200 m、300 m和300 m，外轨超高为120 mm，曲线半径分别为5 500 m、7 000 m和10 000 m，以德国低干扰谱作为轮轨激励，其不平顺如图2所示。

图2 轨道不平顺

2 悬挂参数灵敏度分析

研究表明，动车组转向架悬挂刚度和阻尼等参数对车辆动力学性能影响较大，分析每个悬挂参数对车辆动力学性能的影响，筛选关键悬挂参数进行全面分析[8]。灵敏度分析可以正确选择出对目标函数影响较大的参数，减少待优化变量数目，进而提高优化效率[9]。本文建立的车辆系统动力学模型有12个主要悬挂参数，其名称及符号如表1所示。

表1 主要悬挂参数

利用建立的直线工况，采用最优拉丁超立方抽样方法[10]研究悬挂参数对横向平稳性的影响。若手动将每组样本点导入SIMPACK软件，然后计算并记录横向平稳性的数值需要浪费大量时间，因此建立SIMPACK软件与Isight软件联合仿真计算平台。在Isight中调用2个Simcode组件，第1个Simcode组件为SIMPACK前处理，读取SIMPACK软件的置换变量文件进行模型参数化和自动计算；第2个Simcode组件为SIMPACK后处理，转化计算结果并将计算结果定义为响应。联合仿真计算流程如图3所示。

图3 SIMPACK软件与Isight软件联合仿真计算

经仿真计算得到横向平稳性的灵敏度如图4所示。

图4 横向平稳性的灵敏度

灵敏度为正值时，表示横向平稳性随悬挂参数的增大而增大；灵敏度为负值时，表示横向平稳性随悬挂参数的增大而减小。由图4可知，二系横向减振器阻尼X10对横向平稳性影响最大，灵敏度为50.63%；转臂节点纵向刚度X5和空气弹簧横向刚度X7的影响程度接近，分别为17.45%和13.70%。

3 代理模型的构建及检验

动车组实际运行过程中，温度变化对于橡胶元件和液压减振器的影响较大，引起悬挂参数的变化范围为50%～100%[11]。因此，根据悬挂参数灵敏度分析结果，选取灵敏度绝对值较大的5个悬挂参数作为设计变量，在车辆系统动力学模型中对设计变量进行参数化，各设计变量初始值及取值区间如表2所示。

表2 设计变量取值区间

采用最优拉丁超立方抽样方法抽取100组试验样本点，每组样本均为直线工况下计算横向平稳性，试验设计及横向平稳性实际值如表3所示。

表3 试验设计及实际值

根据表3中100组包含设计变量及其所对应的横向平稳性实际值的样本点，建立Kriging代理模型[12]，再生成10组样本点用于检验代理模型的精度。采用可决系数R2衡量代理模型的精度，其表达式为

(1)

将横向平稳性的实际值和预测值代入式(1)，计算得到Kriging代理模型的可决系数R2为0.96，拟合程度较高，可以进行下一步的分析计算。为了直观地展示Kriging代理模型的拟合精度，绘制横向平稳性实际值和预测值的相关图[14]，如图5所示。

图5 实际值和预测值相关图

由图5可知，用于代理模型精度检验的10组样本点均落在45°对角线附近，说明横向平稳性Kriging代理模型的预测值和实际值相差不大，拟合精度较高。

4 悬挂参数优化及分析

4.1 组合优化策略

全局优化算法虽然能够有效搜索最优解，但计算量较大，寻优时间较长，求解效率降低；数值优化算法求解设计空间连续或单峰函数时效率较高，但是求解多峰函数时依赖于初始设计点的位置，可能会落入局部最优解[15]。为了快速准确地获得全局最优解，本文将自适应模拟退火(adaptive simulated annealing，ASA)算法[16]和非线性序列二次规划(non-linear programming by quadratic lagrangian，NLPQL)算法[17]结合进行参数寻优，发挥ASA算法的全局搜索能力和NLPQL算法的高效局部搜索能力。

ASA算法按照Metropolis准则接受新解，Metropolis准则表达式为

(2)

i为随机的初始解；j为扰动后的新解；F(i)为初始解i的目标函数值；F(j)为新解j的目标函数值；k为玻尔兹曼常数；TK为当前迭代下的温度值。

该算法采用1989年Ingber提出的降温方式[18]，其表达式为

(3)

T0为初始温度；C为给定常数；K为迭代次数；N为设计变量个数。

4.2 数值算例分析

Rastrigin函数是一种典型的复杂对称多峰测试函数，对于有2个独立自变量的Rastrigin函数，其函数表达式为

f(x,y)=20+x2+y2-10(cos2πx+cos2πy)

(4)

x和y的取值范围均为[-5.12,5.12]，测试函数的图像如图6所示，该函数有多个局部极小值点，但只有1个全局最小点(0,0)，该点函数值为0。

图6 Rastrigin函数图像

分别使用ASA算法、NLPQL算法和ASA+NLPQL组合算法求解Rastrigin函数最小值，ASA算法的最大迭代次数为1 000，收敛检验设计数为5，退火和淬火的相对速率参数均为1，初始温度参数为1；NLPQL算法的最大迭代次数为40，收敛精度为10-6。在设计空间中随机选取2个初始点进行优化，优化结果如表4所示。

由表4可知，ASA算法虽然优化效率较慢，但是能够从任意初始点出发接近全局最优点；NLPQL算法收敛速度快，但最优解与初始点的选取有关，容易出现局部最优。ASA+NLPQL组合算法既保证了优化精度，也提高了优化效率，说明该组合优化策略具有可靠性和有效性。

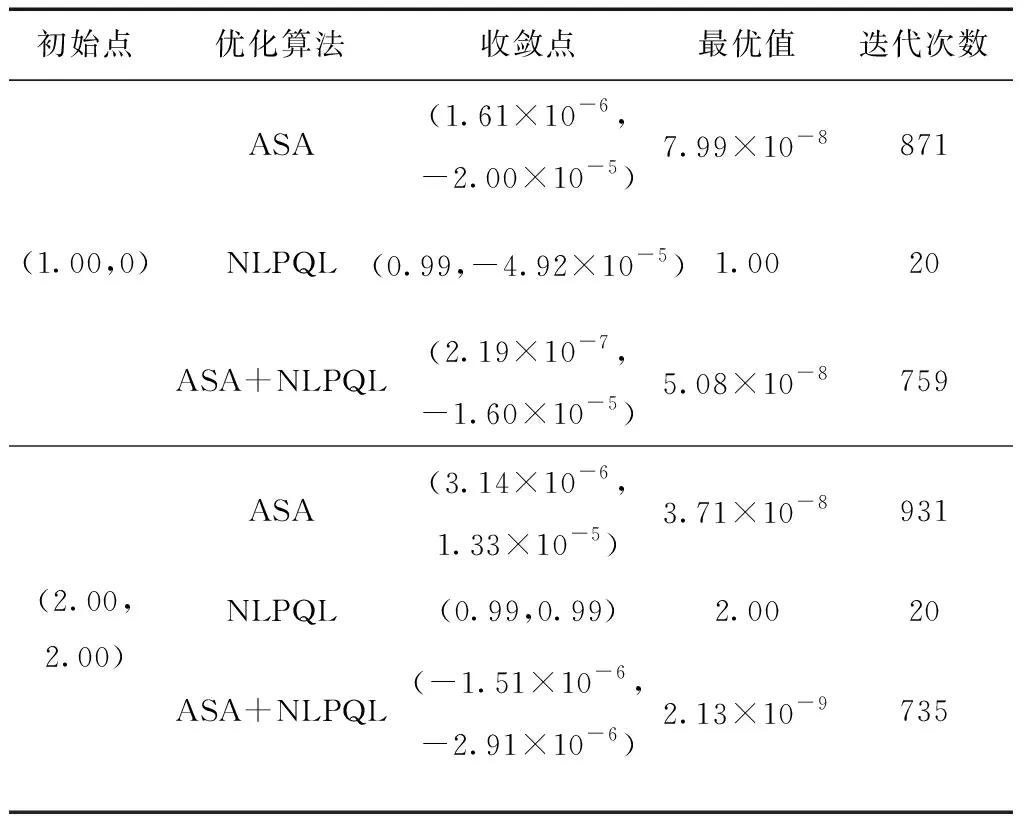
表4 Rastrigin函数优化结果对比

4.3 悬挂参数优化

以悬挂参数为设计变量，以悬挂参数变化范围为约束条件，以横向平稳性最小值为优化目标构建动车组悬挂参数优化模型可描述为

(5)

图7 组合优化策略优化流程

表5 优化前后设计变量及目标函数对比

由表5可知，悬挂参数优化前后横向平稳性得到明显改善，优化率达到18.354%，并且迭代次数为603次，优化效率较高。将最优解的悬挂参数取值输入车辆动力学模型直线工况中，经过计算得到横向平稳性为1.928，实际优化率为12.839%。预测值与实际值之间的误差率为6.328%，小于相对误差的容许值30%，进一步说明代理模型精度满足要求[19]。将最优解的悬挂参数输入车辆动力学模型曲线工况中，计算得到优化前后曲线动力学性能如表6所示。

表6 优化前后曲线动力学性能对比

参考GB/T 5599—2019《机车车辆动力学性能评定及试验鉴定规范》中运行稳定性评定标准，脱轨系数、轮重减载率和轮轴横向力的上限值分别为0.80、0.80和70.59 kN。由表6可知，优化前后车辆运行稳定性均满足要求，不会出现脱轨现象。

5 结束语

提出基于自适应模拟退火算法和非线性序列二次规划算法的组合优化策略对动车组悬挂参数进行优化设计，得到以下结论：

a.横向平稳性灵敏度分析结果表明，二系横向减振器阻尼对横向平稳性影响最大，其次为转臂节点纵向刚度和空气弹簧横向刚度；适当减小对横向平稳性影响较大悬挂参数的数值，有利于车辆平稳运行。

b.通过对比ASA算法、NLPQL算法和ASA+NLPQL组合算法寻求Rastrigin函数最小值的过程，证明了ASA+NLPQL算法的可靠性和有效性。

c.基于组合优化策略的动车组悬挂参数优化过程中，使用Kriging代理模型代替复杂的动力学模型，避免了优化时间较长的问题，提高了计算效率；精度较高的代理模型，保证了优化结果准确性。优化结果表明，横向平稳性实际优化率达到12.839%，横向平稳性得到显著改善，运行稳定性也均满足要求。