基于神经网络的卷烟共线分拣系统自适应控制
刘 方,李 慧,张林岗,胡镕显,吕彦旭
(河南中烟工业有限责任公司南阳卷烟厂,河南 南阳 473005)
0 引言
由于我国独特的地理位置,导致我国烟草产业[1]发达,出口贸易量逐年增加。近年来,人们对异型细支卷烟需求量增高,细支卷烟的销量增长迅速并有超越传统卷烟类型的趋势。异型卷烟[2]的出现不仅创新了烟草产业生产类型,还成功拉动了烟草行业的税率增长。依据相关调查可知,目前烟草生产企业在生产异型卷烟时,主要依靠人工来实施分拣包装,成本高、效率低。卷烟共线分拣系统的提出,有效解决了异型卷烟生产的人工问题。由于该系统为非线性动态系统,因此,需要提出有效的自适应控制方法对系统转换模式开展有效控制。
文献[3]提出一种双拾取动态无线电能传输系统控制方法;文献[4]提出一种结合图像复原技术的自适应光学系统控制方法;文献[5]提出四阶混沌电力系统的协同控制方法。上述方法由于未能依据选定的Lyapunov函数,确定系统的控制规律,导致上述方法在开展系统自适应控制时,控制效果差、控制误差高以及控制性能低。
为解决上述系统控制方法中存在的问题,提出基于神经网络的卷烟共线分拣系统自适应控制方法。
1 控制器设计
1.1 获取系统控制规律
设定卷烟共线分拣系统[6]的非线性函数为g(xp),状态空间α的域内神经网络输出为C(xp),获取过程为
(1)
C(xp)为神经网络的神经元;β(xp)为逼近误差;β0为初始逼近误差。
设定系统跟踪误差为ε,且ε={ε1,ε2,…,εn}T,基于系统线性状态方程xm=Zmxm+χmδc,获取系统信号控制误差,过程为
(2)

基于上述获取的系统状态误差[7],确定系统控制信号,过程为
ξ=-kC(xp)+δg+ηTxp+γδs
(3)
δg为系统的辅助输入信号;ξ为控制信号;ηT、γ为系统参数;k为常数;δs为参考向量。最后基于选定的Lyapunov函数[8],确定卷烟共线分拣系统的控制规律,过程为
(4)

1.2 控制器设计
基于上述确定的系统控制规律[9],建立系统的对象控制模型M(δ)=fp(·),其中,系统的映射平滑函数用fp(·)表述,具体表述形式为
M(δ)=CM(δ-1)+DJ(δ-1)+f0
(5)
C、D为系统的对角参数矩阵;f0为非线性数据项;J为控制参数;δ-1为系统的上一时刻状态。由于建立的模型与实际分拣对象之间存在误差,所以要使ΔJ(δ)=J(δ)-J(δ-1),且DΔJ(δ)=D′J(δ-1),以此定义分拣系统的跟踪误差值,获取控制器的输出值,过程为
(6)
I为对角矩阵;σ(t)为分拣系统跟踪误差;E(t)为控制器参数输入值;M(δ)为系统模型;Jx(δ)为控制器反馈控制系数;Jy(δ)为前馈补偿器[10]。
设计控制器的具体结构如图1所示。

图1 控制器具体设计结构
1.3 控制器训练
依据三层前馈神经网络训练设计的控制器[11],设定神经网络的输出为Sp,获取过程为
(7)
T为迭代函数;mσ为模型训练误差。设定隐含层关系函数为g(Nj),以此获取神经网络的隐含层输出,过程为
(8)
g(Nj)为网络隐含层输出;f0(W)为最终网络输出;W为权值系数;θj为阈值。依据训练输出结果修正控制器参数误差[12]。
2 卷烟共线分拣系统自适应控制方法
基于上述设计的控制器,将卷烟共线分拣系统的控制方法分为线性自适应与非线性自适应2种算法,通过生成的切换机制,实现系统的自适应控制。
2.1 线性自适应控制算法
通过设计的控制器,建立控制器的参数辨识方程,结果为
h(k+d)=X(a-1)h(k)+Y(a-1)uk+
ι[G(k)]=φTG(k)+ι[G(k)]
(9)
Y(a-1)为控制器的非线性函数;ι[G(k)]为非线性项;X(a-1)为控制器多项系数;h(k)为系统输出;uk为输入;φT为常数项;d为系统时滞。
依据上述建立的控制器参数辨识方程,构建系统的线性估计模型,并完成该模型的控制器输出计算[13],过程为
(10)
φ1(k)为控制常数项;h′(k+d)为建立的线性估计模型;φ1(k)TG(k)为模型输出;ϑ、ε分别为参数;u1(k)为模型输入。使用辨识算法对预估模型参数修正处理,以此保证系统输入、输出信号有界,结果为
(11)
φ1(k)为线性模型参数修正结果;u1(k)为约束条件;ε1(k)为辨识误差;J为信号界线。
最后通过修正的线性模型,训练系统参数,完成卷烟共线分拣系统的自适应控制。
2.2 非线性自适应控制方法
基于获取的参数辨识方程,对模型粗略估计,依据ANFIS特性获取系统的非线性定义域,由于该方法无法保证系统的信号界线,所以要依据映射算法将控制器的非线性项映射到函数定义域中,并根据映射结果使用参数调节法调节控制器相关参数[14],过程为
(12)

φ2(k)TG(k)=ϑ(k+d)-
(13)

使用辨识算法修正模型参数误差,获取分拣系统的辨识误差值,过程为
(14)

2.3 建立切换机制
由于系统在卷烟制造时,无法自动控制2种方法的转换,所以需要建立算法切换机制,帮助系统实施相关转换。
建立一个适用于系统的切换函数,并依据该函数构建系统控制切换规则,过程为
(15)
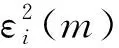
2.4 控制流程
卷烟共线分拣系统的自适应控制流程如下:
a.通过分析卷烟共线分拣系统获取系统控制规律,完成系统的控制器设计。
b.依据控制器的参数识别方法提出线性和非线性2种自适应控制方法。
c.通过建立的控制切换规则,完成线性和非线性算法的切换,从而实现卷烟共线分拣系统的自适应控制。
3 实验
为了验证本文系统自适应控制方法的整体有效性,采用本文方法、双拾取动态无线电能传输系统控制方法(文献[3]方法)和结合图像复原技术的自适应光学系统控制方法(文献[4]方法)进行测试;在开展系统自适应控制过程中,设定系统输入信号分别为阶跃信号以及正弦波信号,基于上述3种系统自适应控制方法对系统实施控制,测试3种方法的控制效果以及控制误差,从而证明3种方法的控制有效性。
3.1 输入信号为阶跃信号控制有效性测试
采用本文方法、文献[3]方法以及文献[4]方法对系统展开自适应控制时,设定系统的输入信号为阶跃信号,系统的最佳输出量为1,测试3种方法的控制效果以及控制误差,结果如图2~图3所示。

图2 阶跃信号下不同控制方法的控制效果

图3 阶跃信号下不同控制方法的控制误差
到达系统最佳输出量的时间越短,证明控制方法的控制效果越好,反之则越差。
由图2可知,本文方法能够快速到达系统最佳输出量并维持系统稳定输出,而文献[3]方法到最佳系统输出时间需要200 s,文献[4]方法到达最佳系统输出需要300 s。由此可知,本文方法能够在短时间内使系统输出到达最佳输出量,主要是因为本文方法依据选定的Lyapunov函数确定了系统的控制规律,所以在实施系统自适应控制时的控制效果好。
由图3可知,本文方法在实验初期测试出的控制误差较大,但是随着测试时间的增加,误差逐渐减小,并将控制误差维持在固定数值内。文献[3]方法需要将近400 s,才能将控制误差锁定在0.02,文献[4]方法则需要500 s,将误差平稳控制。由此可知,本文方法控制系统时,能够快速地将系统分拣误差收敛至0.02,证明本文方法的控制误差小。
3.2 输入信号为正弦波信号控制有效性测试
采用本文方法、文献[3]方法以及文献[4]方法对系统展开自适应控制时,设定系统的输入信号为正弦波信号,系统的最佳输出量同样为1,测试3种方法的控制效果如图4所示。

图4 正弦波信号下不同方法的控制效果
由图4可知,正弦波信号下,控制方法测试出的控制效果低于阶跃信号的系统控制效果,但本文方法的控制效果依然高于文献[3]方法以及文献[4]方法。
设定系统初始控制误差为0.25,正弦波信号下不同控制方法的控制误差测试结果如图5所示。

图5 正弦波信号下不同方法的控制误差
由图5可知,系统输入为正弦波信号时,测试出的控制误差高于阶跃信号的控制误差测试结果。本文方法检测出的控制误差低于其他2种方法,且能快速到达理想最佳误差值,说明本文方法在开展系统控制时的控制误差小。
综上所述,本文方法在系统自适应控制时,控制效果好、控制误差小,证明本文方法的控制性能高。
4 结束语
针对传统系统自适应控制方法中存在的问题,提出基于神经网络的卷烟共线分拣系统自适应控制。该方法依据对系统控制器的设计,建立线性以及非线性2种自适应控制方法;通过制定的切换规则,实现系统的自适应控制。该方法由于在设计控制器时,存在微小误差,今后会针对该项缺陷继续优化该控制方法,直至方法完善。

