HST2425钛合金动态力学行为及本构模型

郭峰挺，丛良超，郭新虎，杜菲菲，孙旭东,3

(1. 东北大学 材料科学与工程学院 材料各向异性与织构教育部重点实验室，辽宁 沈阳 100819;2. 沈阳中钛装备制造有限公司，辽宁 沈阳 110020； 3. 东北大学 佛山研究生院，广东 佛山 528311)

Ti-Al-V-Fe系α+β型HST2425钛合金的密度低、比强度高、抗腐蚀性强，在航天航空和兵器领域具有很高的应用前景[1-2]。与Ti-6Al-4V系TC4钛合金相比，其使用价格较低的Fe替代一部分原本较珍贵的V，性能依然十分优异，是一种低成本、高价值的新型钛合金，具有很高的应用价值。在其服役过程中难以避免受到军事武器的打击，其产生的动态载荷与准静态相比表现出复杂的力学行为[3]。因此，研究其在动态载荷冲击作用下的力学响应显得尤为重要。确定材料在变形过程中的流变应力与应变、温度及应变速率的关系丰富了α+β型钛合金动态力学响应的研究，构建本构模型是材料加工、仿真模拟的基础，关于HST2425钛合金的相关研究目前还未见报道。

尽管用来预测材料在动态冲击下的本构模型有很多[4-8]，但在爆炸及高速碰撞中的有限元模拟中，往往涉及到材料的大变形、断裂过程，Johnson-Cook(J-C)模型由于材料参数少、精度高，常被用于描述金属材料的动态变形行为[9]。很多研究人员试图提出一些改进的Johnson-Cook(J-C)模型，以实现更高的预测精度。Gao等[10]对Ti-6Al-4V合金薄板热拉伸进行了6种本构方程的建立及对比分析，并提出了一种新的TC4钛合金Johnson-Cook(J-C)本构模型，增加了温度校正函数。Yu等[11]对近α型TA23钛合金进行了动态冲击试验，发现温度和应变速率在动态冲击压缩过程中具有交互作用，并建立了原始的Johnson-Cook(J-C)模型及其修正模型，修正后的模型预测结果与试验数据更接近。Zhang等[12]通过修改Johnson-Cook(J-C)本构模型中的应变速率硬化项，得到了7075-T6铝合金的改进Johnson-Cook(J-C)本构模型。Qian等[13]修改了应变速率强化项和温度软化项得到一种新的Johnson-Cook(J-C)本构模型，能较好地描述CuCrZr合金的压缩动力学性能。Lin等[14]首次提出了考虑应变、应变速率和变形温度耦合效应的修正Johnson-Cook(J-C)模型来描述铁基合金钢的拉伸行为，并通过计算方法得出应变、应变速率和变形温度并不是独立的。苏楠等[15]用绝热温升项修正了Johnson-Cook(J-C)本构模型，进行非线性拟合构建了TC2钛合金在室温下的动态塑性本构关系。综上所述，研究人员根据自己的试验数据提出了多种不同的修正J-C模型。这是因为不同材料的变形机理和动态变形机制不同。因此，建立新材料修正模型的关键是根据材料的动态变形行为采用更合适的模型方程，而不是使用统一的模型。本文研究了HST2425钛合金在高应变下流变应力特征和J-C本构模型，使用分离式霍普金森杆(SHPB)装置进行动态压缩和拉伸试验，建立原始J-C模型和改进的J-C模型，可用于预测HST2425钛合金的动态变形行为。

1 试验材料及方法

试验用材料为7 mm厚HST2425轧制板材，化学成分如表1所示，其显微结构为拉长的初生α相+晶间β相构成，如图1所示，其中亮色区域是α相，暗色区域是β相。为了得到强度更高、性能均匀的双相钛合金，将原材料在930 ℃固溶1 h，然后在空气中快速冷却，得到的显微组织如图2所示。可以看出，经过固溶处理后，HST2425钛合金为均匀的双态组织。

表1 HST2425钛合金的化学成分(质量分数，%)

图1 HST2425钛合金的原始显微组织(a)轧制方向；(b)厚度方向Fig.1 Original microstructure of the HST2425 titanium alloy(a) rolling direction; (b) thickness direction

图2 固溶后HST2425钛合金的显微组织(a)轧制方向；(b)厚度方向Fig.2 Microstructure of the HST2425 titanium alloy after solution treatment(a) rolling direction; (b) thickness direction

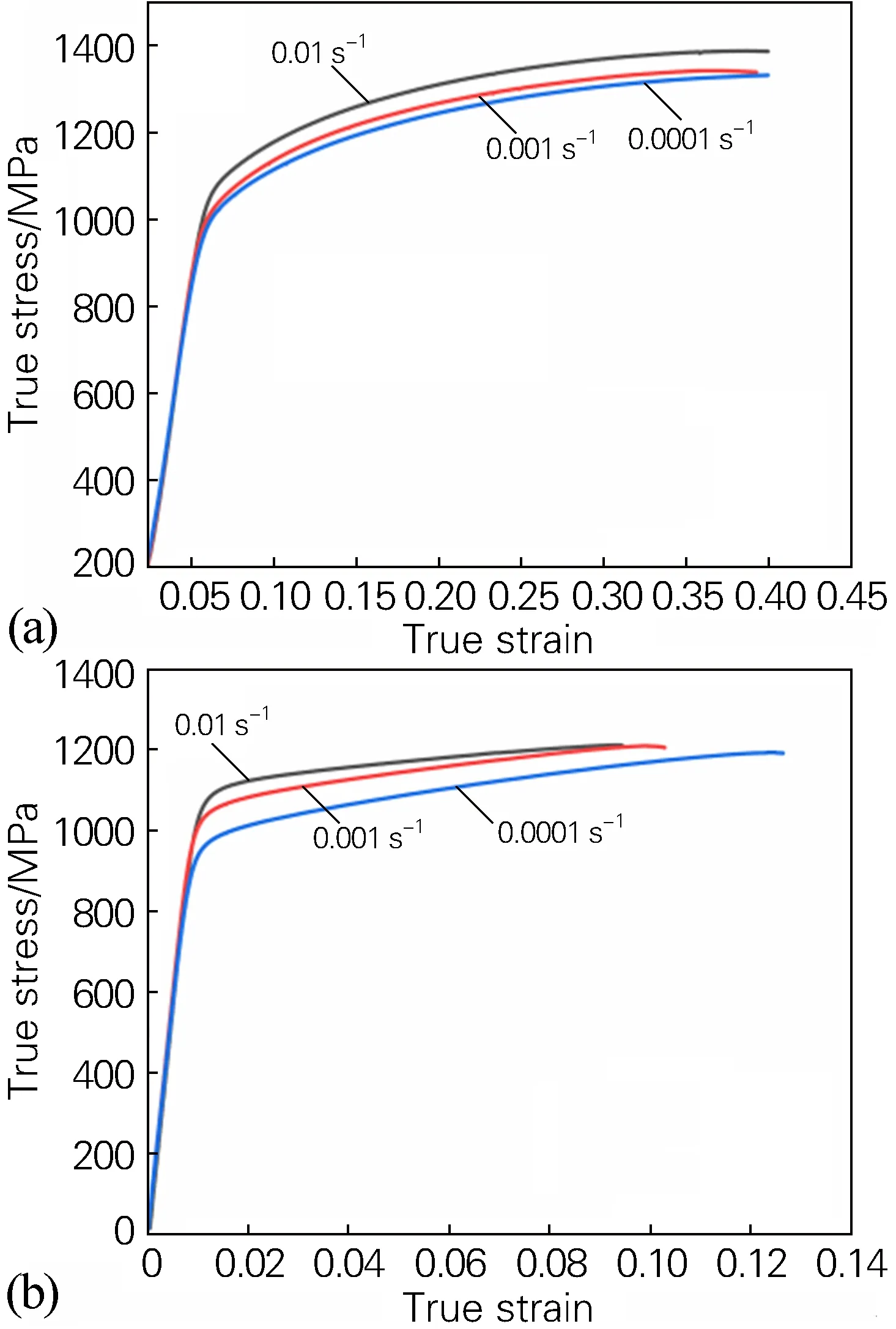
图3 HST2425钛合金在准静态下的真应力-真应变曲线(293 K)(a)压缩；(b)拉伸Fig.3 True stress-true strain curves of the HST2425 titanium alloy under quasi-static state(293 K)(a) compression; (b) tension

依据GB/T 228.1—2010《金属材料 拉伸试验第1部分：室温试验方法》和GB/T 7314—2017《金属材料 室温压缩试验方法》，在AG-XPLUS系列万能试验机上进行HST2425钛合金的常温准静态拉伸、压缩试验，应变速率为0.0001～0.01 s-1。高应变速率动态拉伸、动态压缩试验在SHPB装置上进行，动态拉伸使用圆柱形标准试样，应变速率控制在1900 s-1附近，动态压缩使用直径φ3 mm、厚度3 mm圆柱形试样，由慢走丝线切割和精密磨床加工而成，动态压缩的应变速率控制在1600、3500、5500和6500 s-1附近，对每种应变速率至少进行3次试验，以保证结果的准确性。

2 试验结果

2.1 真应力-真应变曲线

HST2425钛合金在293 K、不同应变速率下的压缩、拉伸真应力-真应变曲线如图3所示，可以看出，无论是拉伸还是压缩，其真应力-真应变曲线均随应变速率增加向上移动，塑性段的流变应力、屈服强度随应变速率的提高而增大。屈服后，流变应力随应变增加逐渐增大，表现出明显的加工硬化行为。这是由于金属变形程度增加时，材料内部晶粒发生畸变和破碎，位错密度增加，从而阻碍了内部晶体滑移，增大了金属塑性变形抗力[16]。图4为293 K下拉伸和压缩应力状态下材料动-静态力学性能的比较，可以看出，材料有着明显的应变速率效应，无论是拉伸或是压缩，其动态下的真应力-真应变曲线相对静态而言均明显上移。

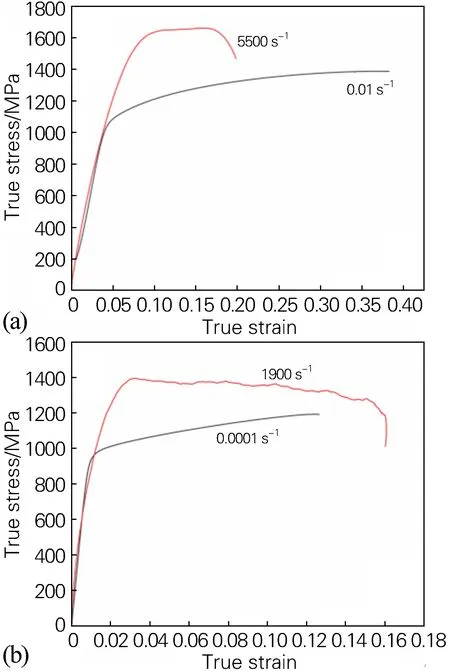
图4 HST2425钛合金动态-静态真应力-真应变曲线(293 K)(a)压缩；(b)拉伸Fig.4 Dynamic-static true stress-true strain curves of the HST2425 titanium alloy(293 K)(a) compression; (b) tension

图5 不同变形温度和应变速率下HST2425钛合金的动态压缩真应力-真应变曲线Fig.5 Dynamic compression true stress-true strain curves of the HST2425 titanium alloy under different deformation temperatures and strain rates(a) 1600 s-1; (b) 3500 s-1; (c) 5500 s-1; (d) 6500 s-1

HST2425钛合金在不同温度和应变速率水平下的动态压缩真应力-真应变曲线如图5所示，可以看出，在弹性阶段流变应力线性增加，屈服后流变应力曲线在塑性变形阶段表现出增大趋势。在弹性阶段，曲线的斜率随着变形温度的升高而减小，这意味着HST2425钛合金的弹性模量在此过程中有所降低。在相同应变速率下，流变应力随着温度的升高而减小，表明HST2425钛合金随着温度的升高而软化。换言之，动态冲击变形伴随着热激活过程。屈服后，流变应力随应变增加有一定增大，表现出加工硬化行为。应变速率提高时，一定范围内HST2425钛合金具有一定的应变速率敏感性，最大应力和最大应变均随应变速率的增大而增加，但是最大应力在应变速率超过3500 s-1后的增加程度降低，最大应变在应变速率超过5500 s-1后的增加程度也降低。此外，流变应力随变形温度的变化如图6所示，可以看出，在相同的应变(0.1)下，不同应变速率下的流变应力递减速度并不相同，说明动态冲击载荷下两个参数之间存在交互作用。

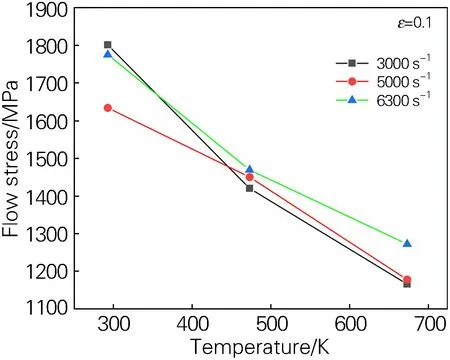
图6 不同应变速率下HST2425钛合金的流变应力随变形温度的变化Fig.6 Variations of flow stress with deformation temperature of the HST2425 titanium alloy at different strain rates

2.2 原始J-C模型

原始J-C模型表达式[11]为

(1)

通过应变速率为0.001 s-1、温度为293 K的准静态压缩试验可以得出A=970 MPa，在293 K和0.001 s-1的变形条件下，式(1)可简化为：

σ=A+Bεn

(2)

式(2)可变换为：

ln(σ-A)=lnB+nlnε

(3)

进而可以根据293 K温度、0.001 s-1应变速率下的流变应力值和应变来计算ln(σ-A)和lnε的值，如图7(a)所示，再通过线性拟合计算得到B=590 MPa，n=0.424。

在变形温度为293 K下，式(1)可简化为：

(4)

式(4)可变换为：

(5)

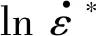
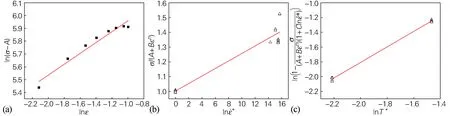
图7 基于原始J-C模型的线性拟合结果Fig.7 Linear fitting results based on the original J-C model

将式(1)变换为

(6)

选择温度为473 K和673 K，应变速率为3500 s-1的流变应力代入式(6)的两边，如图7(c)所示，通过线性拟合结果得到m=1.05。

将所得参数A=970 MPa、B=590 MPa、n=0.424、C=0.025 42、m=1.05代入式(1)，得到HST2425钛合金原始J-C模型为：

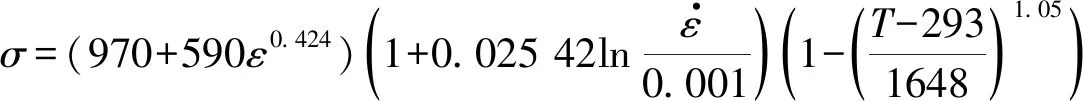
(7)

2.3 修正J-C模型

在原始J-C模型中，应变、应变速率、温度的影响分别是用3个独立的方程表示，然后直接相乘，即不考虑这些因素的交互作用。本文使用一种考虑了影响因素交互作用的修正J-C模型[11]，如式(8)所示：

(8)

式中：A、B1、B2、C、λ1、λ2、λ3为材料常数，其余与原始J-C模型相同。

在变形温度为293 K和应变速率为0.001 s-1的条件下，式(8)可简化为：

σ=A+B1ε+B2ε2

(9)

在此条件下对σ和ε进行二次多项式拟合，如图8(a)所示，由此得到A=1025 MPa，B1=1751 MPa，B2=-2436 MPa。

在变形温度为293 K下，式(8)可简化为：

(10)

式(10)可变换为：

(11)

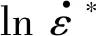
将式(8)变换为：

(12)

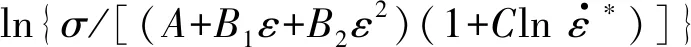
将所得参数A=1025 MPa、B1=1751 MPa、B2=-2436 MPa、C=0.0265、λ1=0.165、λ2=-0.0224、λ3=0.000 757代入式(8)，得到HST2425钛合金的修正J-C模型为：

(13)

图8 基于修正J-C模型的拟合结果Fig.8 Fitting results based on the modified J-C model

图9 不同应变速率下HST2425钛合金流变应力预测值和试验值的比较Fig.9 Comparison between predicted values and experimental values of flow stress of the HST2425 titanium alloy at different strain rates(a) 0.001 s-1; (b) 1600 s-1; (c) 3500 s-1; (d) 5500 s-1

3 分析与讨论

利用原始J-C模型和修正后的J-C模型对HST2425钛合金在冲击载荷下的流变应力进行了预测，并将两种模型的预测值与试验值进行了比较，如图9所示。图10可直观地表述试验值E和预测值P之间的相关性。采用式(14)计算两种模型在不同温度和应变速率下的相关性系数R，结果分别如表2和表3所示。

(14)

由图9可以看出，修正模型的预测值更接近试验值，说明二次多项式函数关系更适合描述HST2425钛合金的变形行为。这与其他学者的研究相似[11,17-18]。由图10可以看出，在应变速率为0.001～5500 s-1和变形温度为293～673 K的条件下，修正模型比原始模型更加准确。由表2和表3可以得出，修正模型与试验值数据相关性更好。这是因为在原始模型中影响因素是相互独立的，而温度和应变速率之间的交互作用确实存在，在修正模型中考虑了它们的交互作用。根据研究人员提出的几种考虑工艺参数相互作用的改进模型[11,17-19]，综合考虑HST2425钛合金动态压缩试验数据，最后得出二次修正模型更适合描述动态冲击载荷下HST2425钛合金的变形行为。

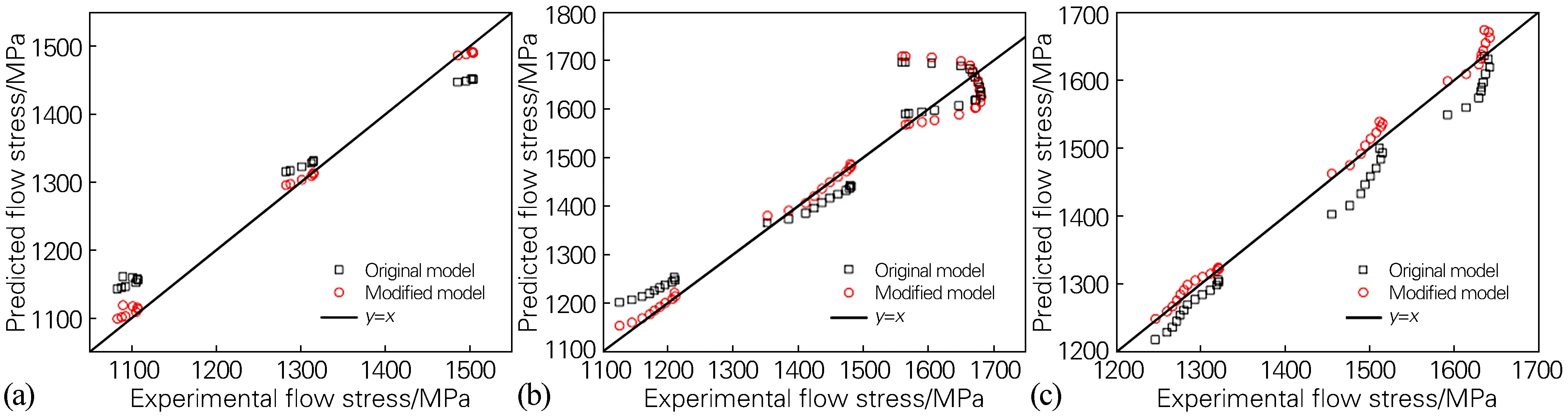
图10 不同应变速率下HST2425钛合金流变应力预测值和试验值的相关性Fig.10 Correlation between predicted values and experimental values of flow stress of the HST2425 titanium alloy at different strain rates(a) 1600 s-1; (b) 3500 s-1; (c) 5500 s-1

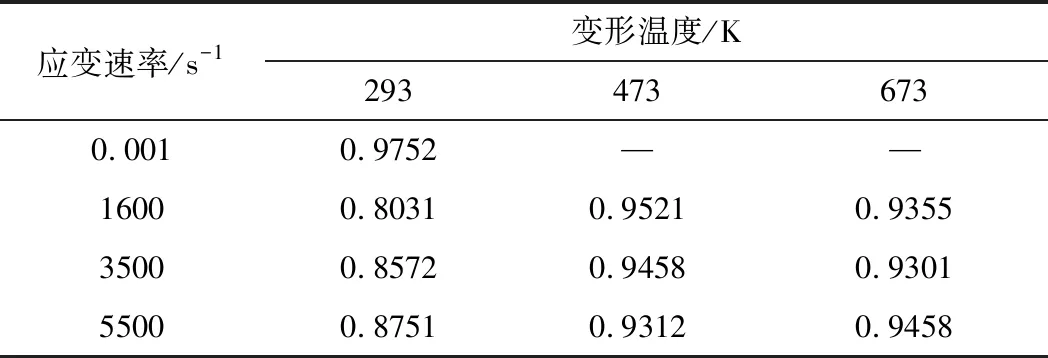
表2 原始J-C模型流变应力预测值和试验值的相关系数R

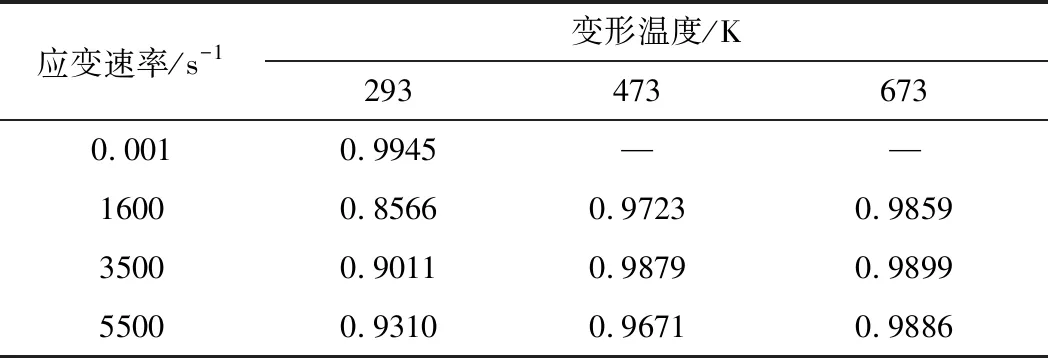
表3 修正J-C模型流变应力预测值和试验值的相关系数R

4 结论

1) 无论在拉伸还是压缩，HST2425钛合金在动态载荷下的流变应力比准静态下的都有明显提高。动态压缩过程中，流变应力随着变形温度的升高而显著降低，最大应力和最大应变均随应变速率增大而增加，但是应变速率超过3500 s-1后应力增加的程度降低，应变速率在5500 s-1后应变增加的程度也降低。同时，变形温度和应变速率对流变应力有交互作用。

2) 建立了HST2425钛合金的原始J-C模型和考虑了温度和应变速率之间的交互作用的J-C修正模型，其中修正模型与真实数据的相关性更好，较原始J-C 模型更适合预测HST2425钛合金的动态冲击变形行为。