基于深度学习的完全填充型熔融沉积成型零件质量预测方法

董 海，高秀秀，魏铭琦

(1.沈阳大学 应用技术学院，辽宁 沈阳 110041；2.沈阳大学 机械学院，辽宁 沈阳 110041)

0 引言

增材制造(Additive Manufacturing, AM)是20世纪80年代诞生的快速成型技术，通过连续添加材料层的方式实现3D数字模型到物理模型的转换，与传统减法制造(切削加工)相比更具节能、绿色和可循环等特点[1-2]，符合产品快速开发和个性化定制的市场需求。熔融沉积成型(Fused Deposition Modeling, FDM)因其成型设备简单、生产成本低和无需多余工具即可制造复杂零件等关键驱动因素，成为国内外应用最为广泛的增材制造技术之一[3-4]。但FDM技术仍面临挑战，其特定的成型技术和工艺参数导致产品表面呈现出明显的纹路和质感，使得零部件的综合精度和力学性能下降[5]。针对以上问题，许多研究集中于理解和优化FDM工艺参数，以增强产品的性能特征，扩展FDM技术的应用领域。WANG等[6]对翘曲变形印刷零件进行了建模，模型考虑FDM的材料属性和机器设置，例如层厚、打印路径、挤出温度和速度，指出改善温度和打印路径可以有效减少翘曲变形。NANCHARAIAH等[7]通过田口方法和ANOVA技术研究了光栅角度、涂层厚度和宽度对FDM零件表面粗糙度的影响，提出层厚会显著影响FDM零件的精度；SAHU等[8]等分析了层厚、打印方向、光栅角度、光栅宽度和气隙等工艺变量对零件表面精度的影响及其相互作用。传统质量方法和数学建模虽然可以验证工艺参数对产品某一性能的影响，但难以准确建立输入变量与输出变量之间的映射关系，因此对产品质量的改进效果并不明显。

神经网络因其强大的数据和非线性处理能力被应用于FDM零件性能预测。通过构建基于神经网络的质量预测模型，可以实现对产品质量的有效把控，对于优化过程参数和提升产品质量具有重要的意义。为了改善FDM零件表面粗糙度，VAHABL等[9]构建了表面粗糙度分布模型，提出了一种基于径向基函数神经网络的产品表面粗糙度预测方法；ZHANG等[10]以零件抗拉强度作为产品质量指标，构建了基于长短期记忆网络的FDM零件质量预测模型；吴天山等[11]将遗传算法和BP神经网络相结合，建立了FDM工艺参数与制件翘曲变形关系的函数模型，实现制件翘曲量的预测；ALI等[12]采用贝叶斯正则化函数训练人工神经网络模型，将光栅角度、气隙、构造方向和轮廓数量作为输入变量，完成对FDM零件的机械性能预测。然而，以径向基函数神经网络、长短期记忆网络和BP神经网络为代表的浅层机器学习模型虽能实现对FDM零件某一性能的预测，但因其具有的单隐层结构导致对特征信息提取的能力有限，难以准确映射多工艺参数与多质量指标之间的复杂非线性关系，且模型稳定性较差[13]。因而，在进行高维复杂数据预测时，亟需建立一种预测精度更高，稳定性更强的预测模型。

深度信念网络(Deep Belief Network, DBN)是由多个受限玻尔兹曼机(Restricted Boltzmann Machine, RBM)堆叠而成的深层神经网络[14]。相对于单隐层结构的神经网络，DBN的学习效率更高，预测效果更好[15]。目前，基于DBN的各种深度学习模型被广泛应用于解决许多具有挑战性的问题，如质量预测[16]、故障诊断[17]、流量预测[18]、风能预测[19]、图像分类[20]等。DBN网络对特征信息的提取依赖于RBM，受视觉皮层稀疏表示的启发，稀疏概念被引入RBM中，以便于上层神经元提取刺激中最本质的特征，学习到更有效的特征信息。Lorentz函数稀疏约束已被应用于检测和图像辨别等多个领域，相关实验表明该方法能有效实现对特征信息的提取，同时可以抑制环境噪音[21]。此外，遗传算法、人工蜂群算法和粒子群算法作为常用参数优化方法被引入神经网络中，仿真结果显示，权重和阈值优化后的神经网络的预测性能明显优于未经优化的单一神经网络[22-24]。基于此，本文利用自适应布谷鸟搜索算法优化网络参数，相较于以上智能算法，自适应布谷鸟搜索算法的优势在于算法涉及较少代码和参数，且具有较强的全局搜索能力。

综上，本文将构建一种基于深度信念网络的完全填充型FDM零件质量预测模型，以稀疏约束受限玻尔兹曼机(Sparse Restricted Boltzmann Machine, SRBM)作为其核心组成单元，利用网格搜索和10-倍交叉验证确定模型超参数，采用自布谷鸟搜索(Adaptive Cuckoo Search, ACS)算法优化网络参数。考虑工艺参数配置对完全填充型FDM零件表面粗糙度、翘曲度和抗拉强度的影响，基于ACS-SDBN构建工艺参数与产品质量的映射关系模型，实现对完全填充型FDM零件质量的精确预测，通过实例数据，验证ACS-SDBN预测方法的有效性。

1 稀疏深度信念网络和自适应布谷鸟搜索算法

1.1 稀疏深度信念网络

DBN是一种概率生成模型，由多个RBM结构堆叠而成，低层的RBM通过贪婪方式提取低级特征(线性特征)，而较高层则用于获取样本数据的抽象特征(非线性特征)。RBM和DBN的结构模型如图1所示。

RBM由多个显层神经元(vi)和多个隐层神经元(hj)构成，vi表示第i个显层神经元，i∈n；hj表示第j个隐层神经元，j∈m。显层神经元和隐层神经元被激活的概率为0或1，且采用双向等权方式连接，权重为wi,j，同层神经元相互独立，ai，bj分别表示显层和隐层的偏执阈值。RBM的概率分布可以通过能量函数来实现，在给定状态(v，h)下的能量函数定义为：

(1)

对式(1)进行可视化和正则化，可得RBM的联合概率分布如式(2)所示：

(2)

式中z(θ)为归一化因子，

(3)

式中θ={wij,ai,bj}为网络参数。当显层向量v给定时，隐元j被激活的概率为：

(4)

显元i被激活的概率为：

(5)

其中R表示Relu激活函数，用于激活神经元。其拥有比Tanh激活函数和Sigmoid激活函数更好的特征学习能力。参数的更新规则如式(6)～式(8)所示：

(6)

(7)

(8)

式中：ε为学习率，t为迭代次数，〈〉data表示输入数据，〈〉rec表示重构数据。RBM的训练过程如下：

步骤1导入数据样本、设置网络学习率和隐层层数和神经元个数；

步骤2对网络权重wij和偏置ai、bj初始化；

步骤3采用式(4)计算所有隐层神经元的激活概率，并对hj进行采样；

步骤4采用式(5)计算所有显层神经元的激活概率，并对vi进行采样；

步骤5基于式(6)～式(8)更新权重和阈值，然后转步骤3，直至获得最小的网络误差。

通过对RBM模型添加稀疏约束可以加强对有效特征信息的提取。当前，常用的稀疏分布是广义高斯分布，而柯西分布也具有广义高斯分布特性，且柯西分布具有更好的稳定性[25]。因此，本文采用柯西分布作为稀疏的前项构建SRBM。根据贝叶斯理论，柯西分布的后验分布可以表示为：

(9)

式中：k表示第k层，k∈K;sh表示尺度函数;增加RBM稀疏性的最大后验估计为：

(10)

上式最小化函数的等价表达式如式(11)所示：

(11)

(12)

其中：lS表示稀疏性Lorentz度量，S表示激活概率稀疏性的控制因子。为使模型在学习过程中得到稀疏表示，需对权重和阈值进行调整，以便RBM可以最大化似然函数并获得训练集的稀疏分布。SRBM模型的目标函数如式(13)：

(13)

式中：第二项为似然项，第三项为正则项，λ是正则化参数。LRBM(Lorentz RBM)训练使用对比散度算法获得似然项的近似梯度，并对正则项进行求解。正则项的梯度计算过程如式(14)～式(15)所示：

(14)

(15)

1.2 自适应布谷鸟搜索算法

布谷鸟搜索(Cuckoo Search, CS)算法是由YANG等[26]于2009年提出的一种新的智能优化算法，该算法的优势在于采用Levy飞行机制进行随机搜索，有效平衡了算法的局部搜索能力和全局搜索能力。

根据布谷鸟搜索的一般原理可知，步长控制因子和丢弃概率对布谷鸟的寻优能力具有十分显著的影响:①丢弃概率pa，其值决定了新巢保留的数量，即种群的多样性；②步长控制因子α，其值决定了Levy飞行的收缩范围。在标准布谷鸟搜索算法中，α和pa是固定值，不能很好地调整Levy飞行产生的步长，保证种群的多样性。为此，本文采用递减余弦策略实现pa和α的自适应调整。

自适应丢弃概率的表达式为:

(16)

式中P是位于区间[0,1]中的随机实数，自适应步长控制因子的表达式为：

(17)

式中：R为当前进化代数与总进化代数的比值，即R=t/tmax；a和b为常数，a,b∈(0,1)。因此，基于动态自适应步长的鸟巢位置更新方式可以进一步表示为：

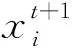
(18)

2 基于ACS-SDBN的完全填充型FDM零件质量预测模型

完全填充型FDM零件质量预测的主要步骤包括关键影响因子筛选、ACS-SDBN预测模型构建、完全填充型FDM零件质量预测。基于ACS-SDBN模型的完全填充型FDM零件质量预测过程如图2所示。

2.1 关键影响因子筛选

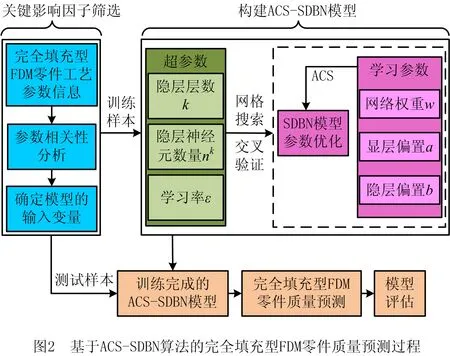
FDM的工作原理为离散堆积原理，其加热喷头受计算机中分层软件控制，在三维平面运动。FDM图像文件一般以STL文件形式储存，计算机对其进行分层处理，并确定材料逐层沉积的路径，送丝机将丝材送至喷头，丝材受热熔化至熔融状态，从喷头流出，沿着预定的打印路径移动沉积熔融材料，挤出的材料随后冷却并形成单个层。一层完成后，支撑平台会降低预定距离，允许沉积更高层，其过程一直持续到产品打印完成。完全填充型FDM零件成型工艺及打印式样如图3所示。

本文以长200mm、宽50mm、高15mm的I字型打印式样为例，实验设备为极光尔沃Z-603S，实验耗材为ABS材料，以原点为起点对其进行水平打印，设定填充密度为100%，该过程包括10个比较重要的工艺参数：喷嘴直径、切片厚度、融化温度、成型室温、挤出速度、填充方式、网格间距、开启延时、关闭延时、扫描速度。然而，对于某一固定的FDM打印设备，大部分工艺参数已经固定，因此，本文所选取切片厚度、挤出速度、扫描速度、融化温度，成型室温这5个在软件中可以修改的常见参数作为零件质量影响因素，研究以上工艺参数配置对完全填充型FDM零件表面粗糙度y1、翘曲度y2和抗拉强度y3的影响。表1给出了以上参数的取值范围。基于正交法打印式样，得到2 500个有效式样，将其中70%的样本作为训练样本，剩余30%作为测试样本，给出部分式样的原始信息如表2所示。

表1 FDM系统工艺参数及范围

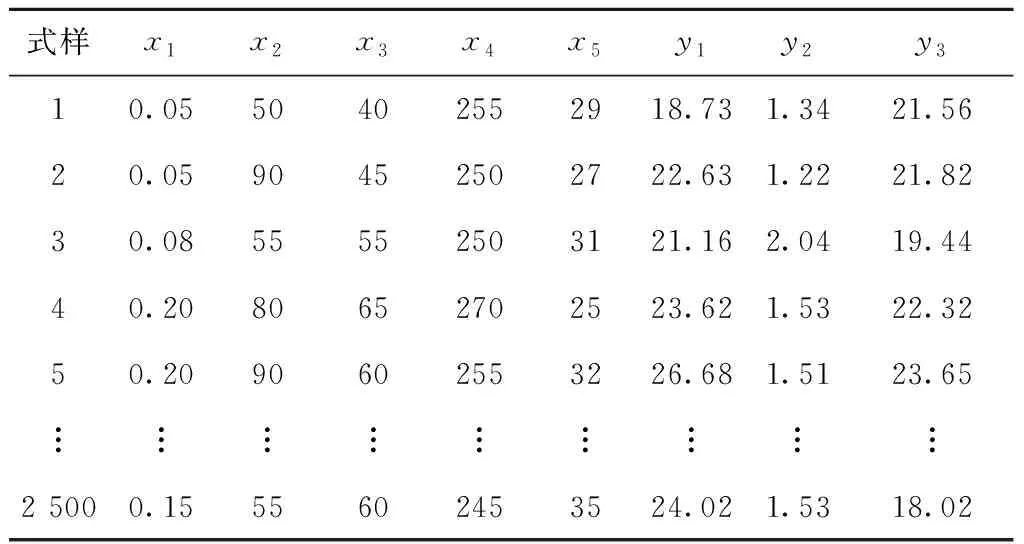
表2 测试样本数据

数据相关性分析有助于检验各工艺参数同零件质量之间的相关性，也可以确定影响零件质量的关键影响因子，避免冗余信息，提高预测结果。为此，本文采用SMILDE等[27]提出的组合相关检验方法(RVmod)来进一步确定影响FDM零件的关键影响因子。RVmod是相关分析(如多元回归分析、主成分分析和典型相关分析)的推广，

A=XXT-diag(XXT)，

B=YYT-diag(YYT)。

(19)

式中：X表示影响因素矩阵，Y表示产品质量指标矩阵。根据式(19)计算不同工艺参数组合与3个质量指标的相关性，确定了相关程度最高的工艺参数组合，即X=[切片厚度，挤出速度，喷头温度，成型室温]，此时获得最高的RVmod=0.83。

2.2 ACS-SDBN质量预测模型构建

本文将ACS-SDBN模型用于完全填充型FDM零件抗拉强度、翘曲度和表面粗糙度预测。通过相关分析筛选出关键影响因素，将其输入SDBN模型的可视层，基于交叉验证和网格搜索确定模型的超参数，并利用ACS算法优化SDBN模型的网络权重w，显层偏置a和隐层偏置b。本文选取平均相对百分比误差(MAPE)来评估预测模型的性能。

(20)

式中：N为样本的数量，fn为预测值，Fn为真实值。

SDBN模型的超参数(学习速率ε、隐层层数k、隐层神经元数量)设置对模型性能有显著影响。目前关于SDBN模型超参数优化的研究中，研究者多采用经验法解决模型的超参数取值问题[28]，而基于经验的取值方法并不能保证所取的超参数值为最优值。为此，本文采用一种穷举搜索方法——网格搜索(GridSearch,GS)搜索SDBN模型超参数的所有可能取值，以交叉验证的验证误差值作为评价标准，确定模型超参数的最佳组合。

在统计分析和机器学习等领域常采用K-折交叉验证(K-foldCrossValidation, K-CV)方法调节参数，评价模型性能[29]。参照文献[30]将训练样本随机划分为10份，取其中1份作为验证集，其余9份为训练集，如此训练10次获得每次的验证误差，误差最小模型对应的超参数为SDBN网络的最优超参数。10-折交叉验证原理如图4所示。

在网格搜索过程中，对不同的隐层层数k和学习率ε进行组合，将10-折交叉验证中抗拉强度、翘曲度和表面粗糙度的平均最小验证误差对应的超参数值作为模型最终选择。SDBN模型超参数的网格搜索结果如图5所示。

基于网格搜索的结果可知，当k=4和ε=0.8时，获得FDM零件质量特性的最优平均验证误差为4.14%，此时，抗拉强度、翘曲度和粗糙度的验证误差分别为4.17%、3.88%、4.35%，4个隐层所包含的神经元数量依次为8、22、15、7。综上，本文构建的ACS-DBN预测模型包含1个显层、4个隐层和1个输出层，模型网络结构为4-8-22-15-7-3，学习率为0.8。

确定模型超参数后，合并训练集和验证集，将其作为已确定网络结构的SDBN模型的训练样本再次训练模型，利用ACS算法优化网络学习参数，以训练误差作为适应度值，得到最优的FDM质量预测模型。ACS-SDBN模型学习参数优化的具体流程如图6所示。

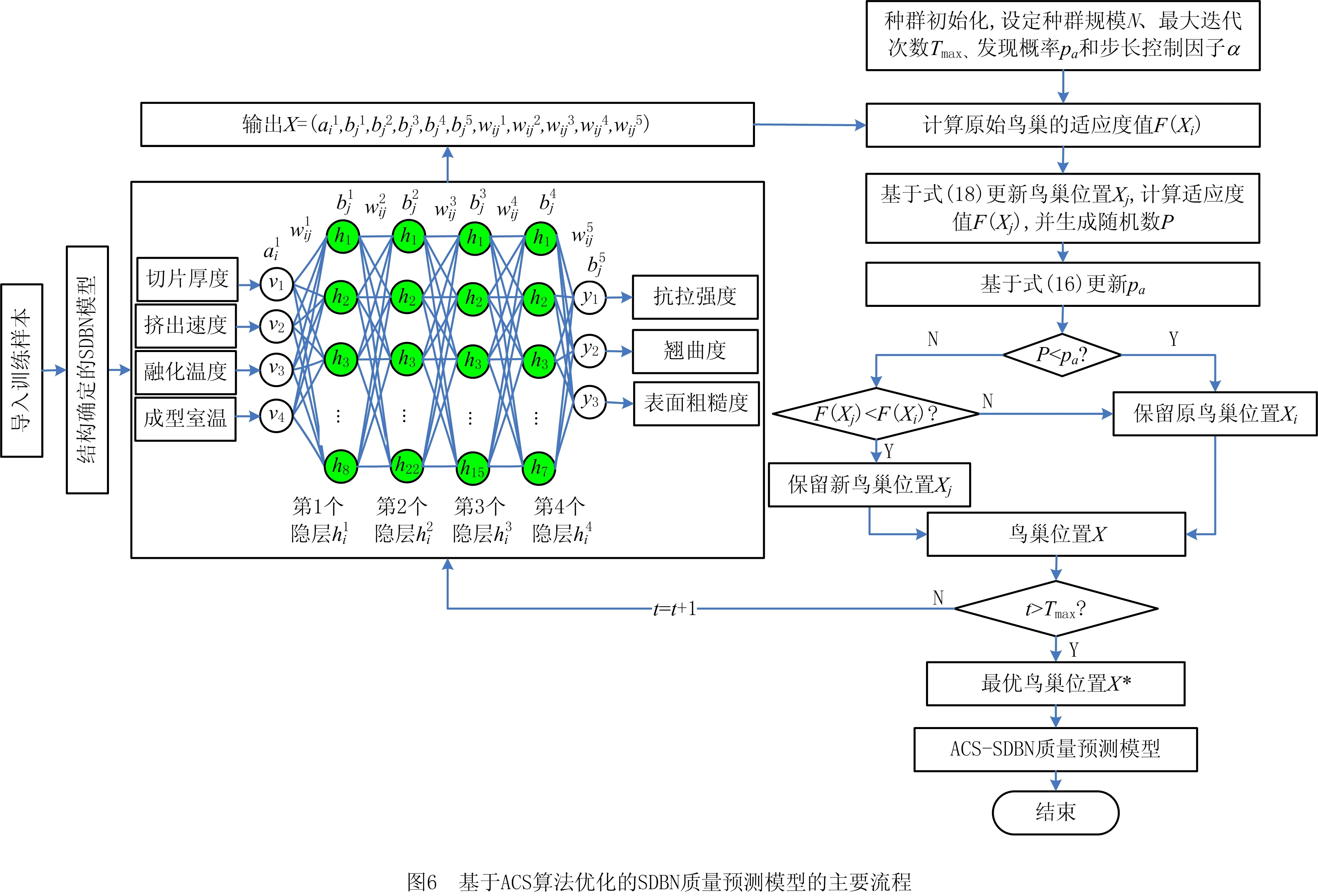
基于ACS-SDBN模型的学习参数优化过程步骤如下：

步骤1初始化ACS的参数，设定种群规模为20，初始步长和发现概率的范围分别为[0.01，0.3]和[0.2，0.5]，a=0.4，b=0.7，迭代200次。

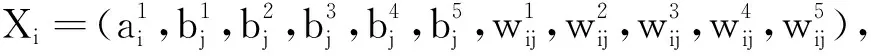
步骤3计算初始鸟巢的适应度值F(Xi)，将训练误差作为适应度函数。

步骤4基于式(18)得到更新后的鸟巢位置Xj，并计算适应度值F(Xj)，生成随机数P，同时根据式(16)更新发现概率pa。

步骤5比较P与pa，当P≤pa时，比较新鸟巢和初始鸟巢的适应度值，保留最优的鸟巢位置；否则，丢弃新鸟巢Xj，保留原始鸟巢Xi。

步骤6输出当前保留的鸟巢位置X，更新迭代次数，转步骤3直至满足输出条件。

步骤7输出最优的鸟巢位置X*，并将其输入SDBN模型，得到最终的SDBN质量预测模型。

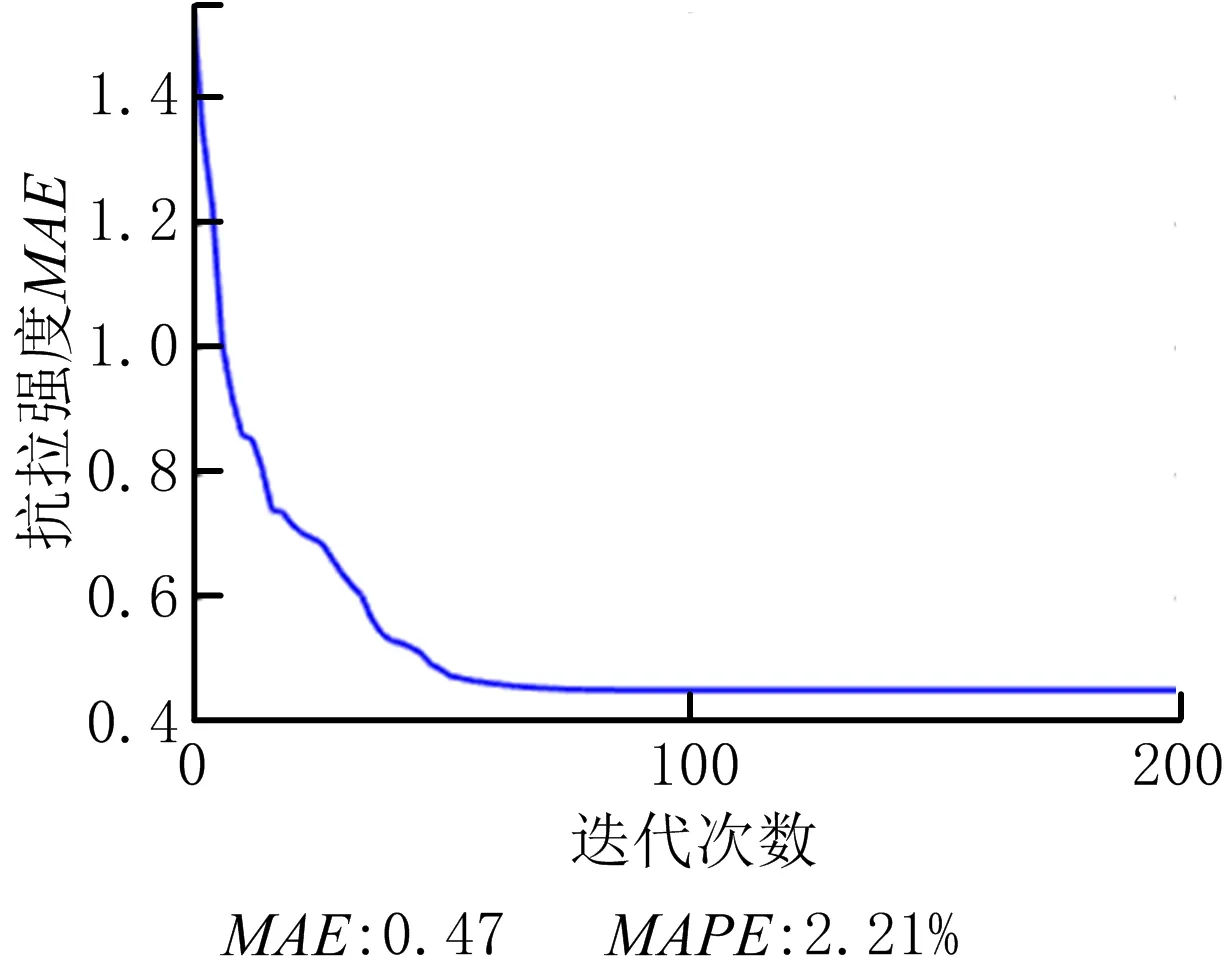
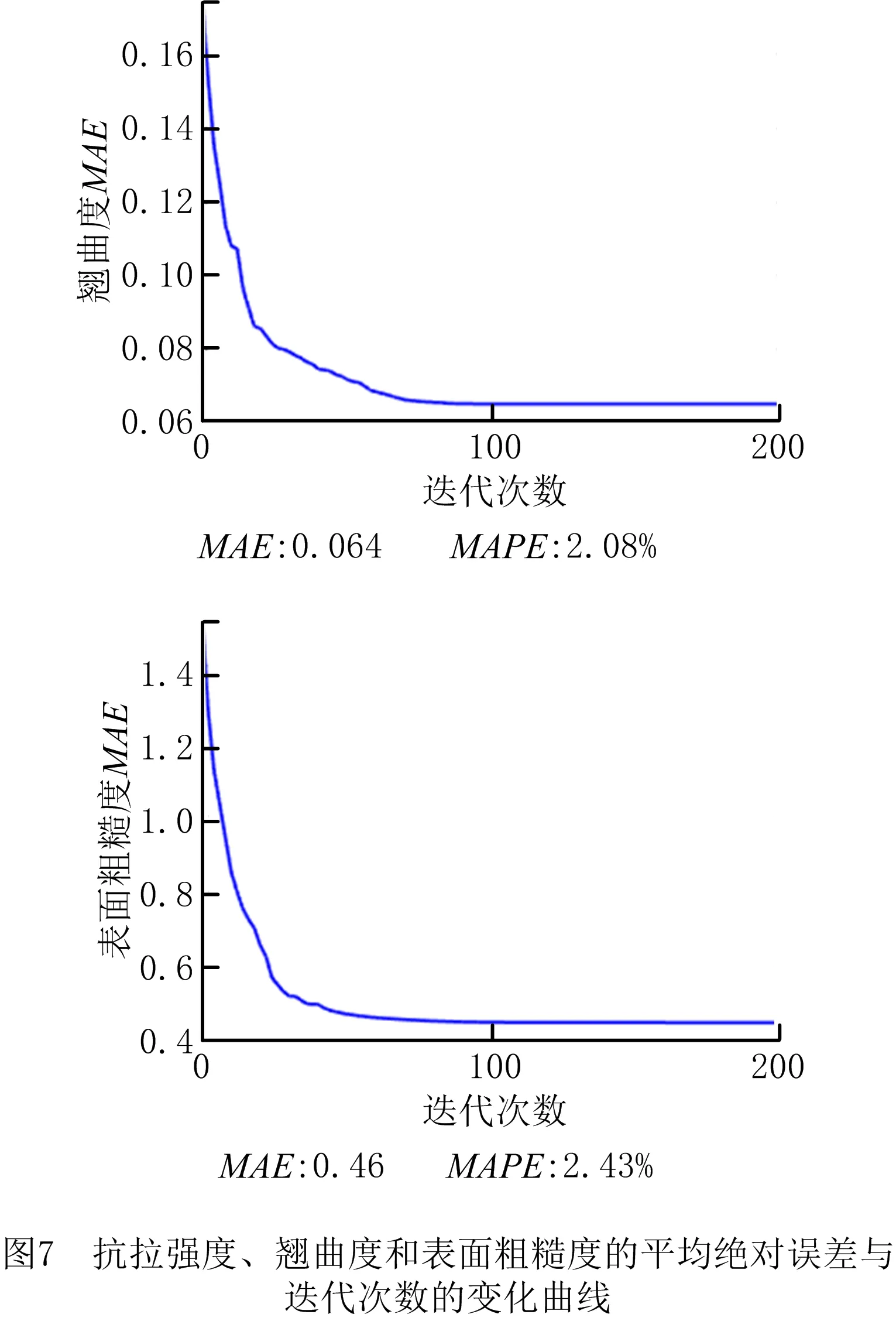
基于ACS-SDBN质量预测模型优化过程的平均绝对误差变化曲线如图7所示。由图可知，完全填充型FDM零件抗拉强度、翘曲度和表面粗糙度的平均绝对误差随迭代次数的增加逐渐减小，最终的误差MAPE为2.21%，2.08%和2.43%。相较于优化前的SDBN模型(图5所示结果：4.17%、3.88%、4.35%)，权重和偏置优化后的模型获得的抗拉强度、翘曲度、表面粗糙度的训练精度分别提高了4.17%-2.21%=1.96%，3.88%-2.08%=1.80%，4.35%-2.43%=1.92%。上述结果充分显示了ACS算法优化参数的有效性。

3 预测结果及分析

为测试本文所提模型的性能，采用ACS-DBN、DBN和BP在同一数据集上预测完全填充型FDM零件抗拉强度、翘曲度和表面粗糙度。采用10—折交叉验证和GS法确定上述模型的超参数，然后导入完整的训练集对模型进行训练，从而确定最终的预测模型，实现对FDM零件3个质量特征的预测。ACS-SDBN、ACS-DBN、DBN和BP模型10—折交叉验证的训练误差和验证误差如图8所示。

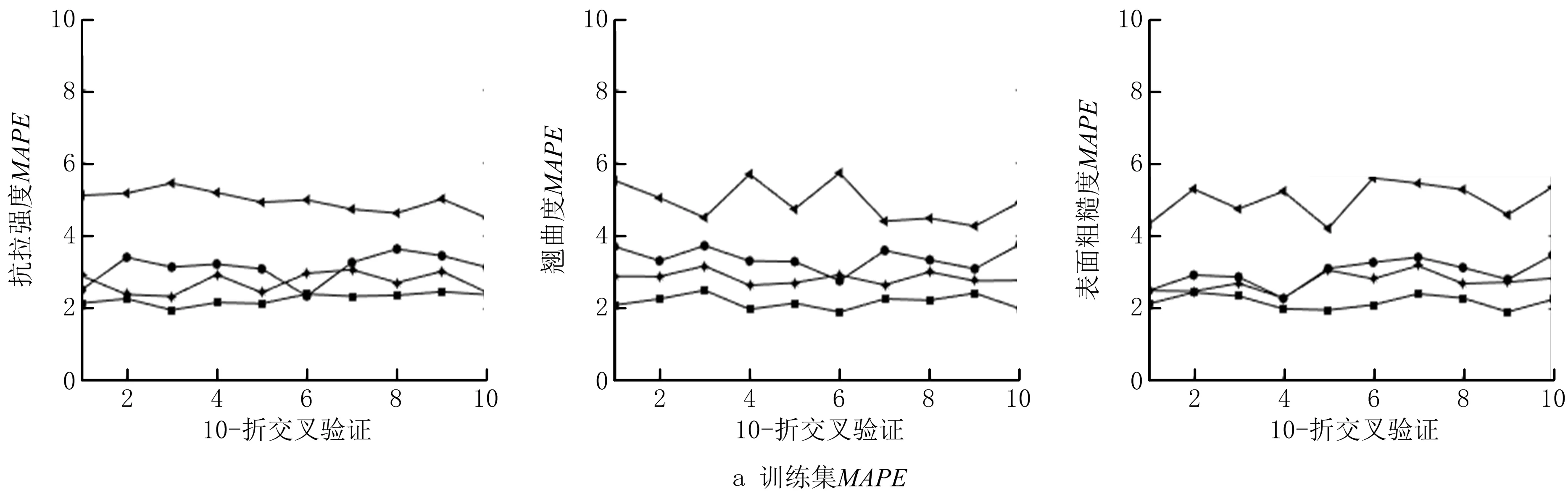
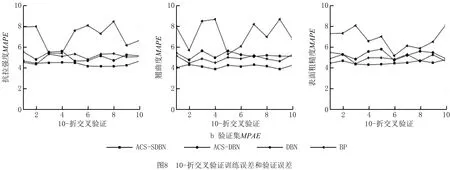
交叉验证不仅可以用于参数调整，而且可以用于模型评价。在图8中，对不同模型的训练误差和验证误差进行了10—折交叉验证。从图中可以看出，ACS-SDBN、ACS-DBN、DBN模型的10—折交叉验证训练误差和验证误差均能保持相对稳定的结果，其中，ACS-SDBN模型10—折交叉验证训练结果最优。BP模型因其单隐层结构，使得其训练误差和验证误差均呈现出明显的波动。与ACS-SDBN、ACS-DBN、DBN模型的稳定结果相比，BP模型的10—折交叉验证误差存在显著差异。进一步，根据表3中的误差统计结果，ACS-SDBN模型下完全填充型FDM零件的抗拉强度、翘曲度和表面粗糙度的10—折交叉验证平均训练误差分别为2.26%，2.17%，2.18%，平均验证误差分别为4.42%，4.14%，4.53%。与ACS-DBN、DBN和BP相比，本文所提模型的精度有明显提高，没有出现过拟合现象，且模型的稳定性较强。

表3 各模型误差结果和运行时间统计

本文保留10—折交叉验证中验证误差最小时的网络参数，然后将整个训练集输入调试后的模型中进行训练，并利用测试集评价模型性能。表3比较了不同模型下完全填充型FDM零件抗拉强度、翘曲度和表面粗糙度的训练误差和测试误差。从实验结果来看，在训练误差方面，ACS-SDBN模型对3个质量特性的训练误差分别为1.96%、1.80%和1.92%，与ACS-DBN模型相比提高了0.59%、0.94%和0.80%；与DBN模型相比提高了0.72%、1.34%和1.00%；比BP模型高了2.56%、2.95%和2.90%。测试误差方面，ACS-SDBN模型仍然能保持优越的预测能力，且与其他模型明显拉开了差距，尤其是与DBN模型和BP模型。ACS-SDBN模型对完全填充型FDM零件的抗拉强度、翘曲度和表面粗糙度的预测误差分别为2.52%、3.06%、2.93%，模型的预测准确性相对于ACS-DBN模型提高了1.16%、1.66%、2.05%；相较于DBN模型提高了2.05%、1.96%、2.50%；比BP模型的预测准确性提高了4.99%、4.54%、4.22%。测试结果表明，本文设计的ACS-SDBN模型能够实现完全填充型FDM工艺参数与零件质量特性之间的准确映射，具有优异的预测性能。

在模型运行时间上，由于自适应布谷鸟搜索算法的引入使得ACS-SDBN和ACS-DBN能在较短的时间内优化网络参数，在提升网络收敛速度的同时也提高了模型的预测精度，因而具有比DBN更小的预测误差和更短的运行时间。ACS-SDBN和ACS-DBN的收敛速度没有显著差别，但SDBN模型具有更强的特征学习能力和映射能力，因而使得ACS-SDBN的预测精度优于ACS-DBN模型。BP神经网络作为浅层神经网络(单隐层结构)，相对于多隐层的DBN模型其学习速度更快，但其对样本特征的学习能力有限，对非线性数据的拟合能力较弱，因此BP模型的能在1.84s内完成网络预测，但其预测精度远低于ACS-SDBN模型的预测精度。

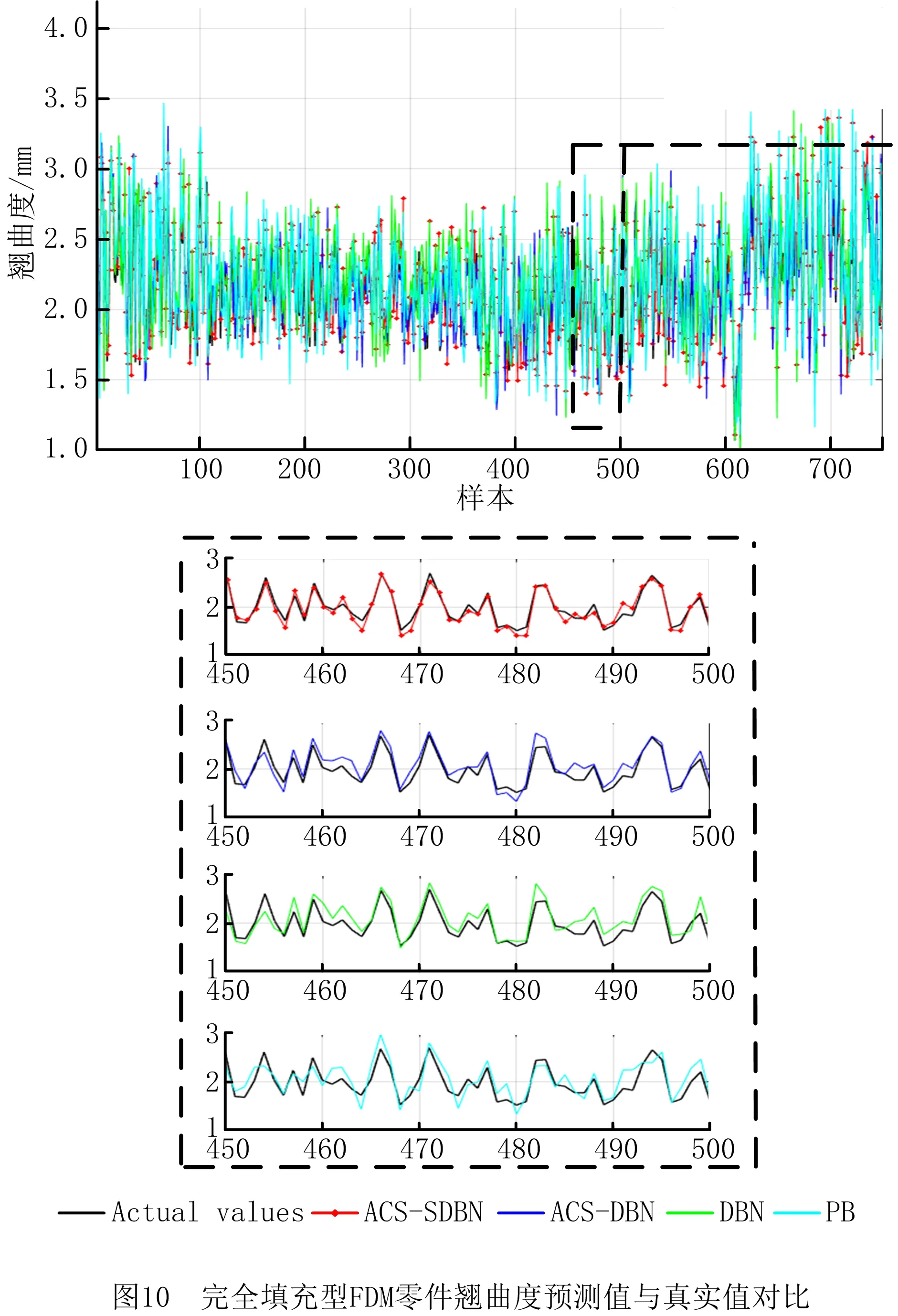
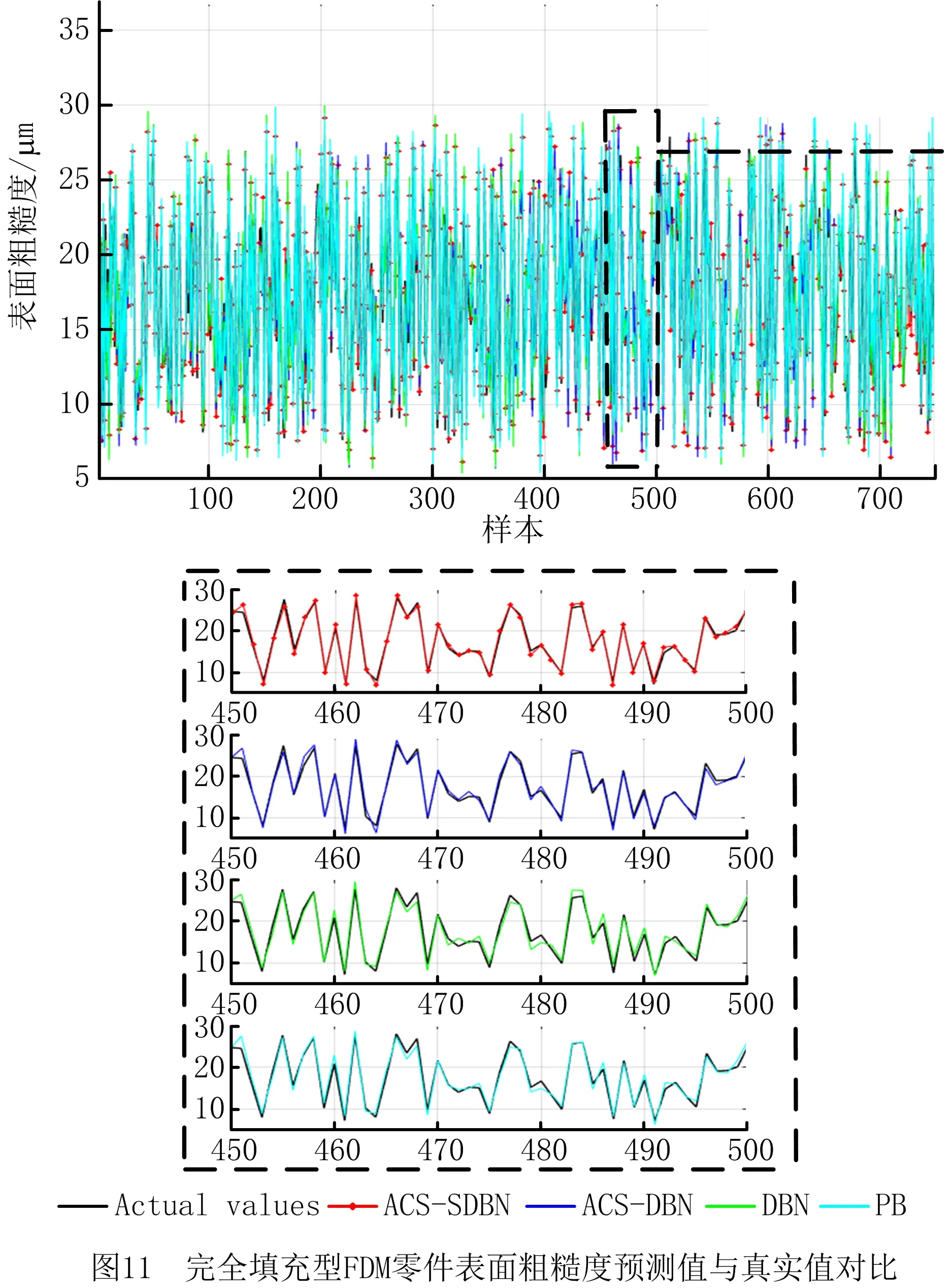
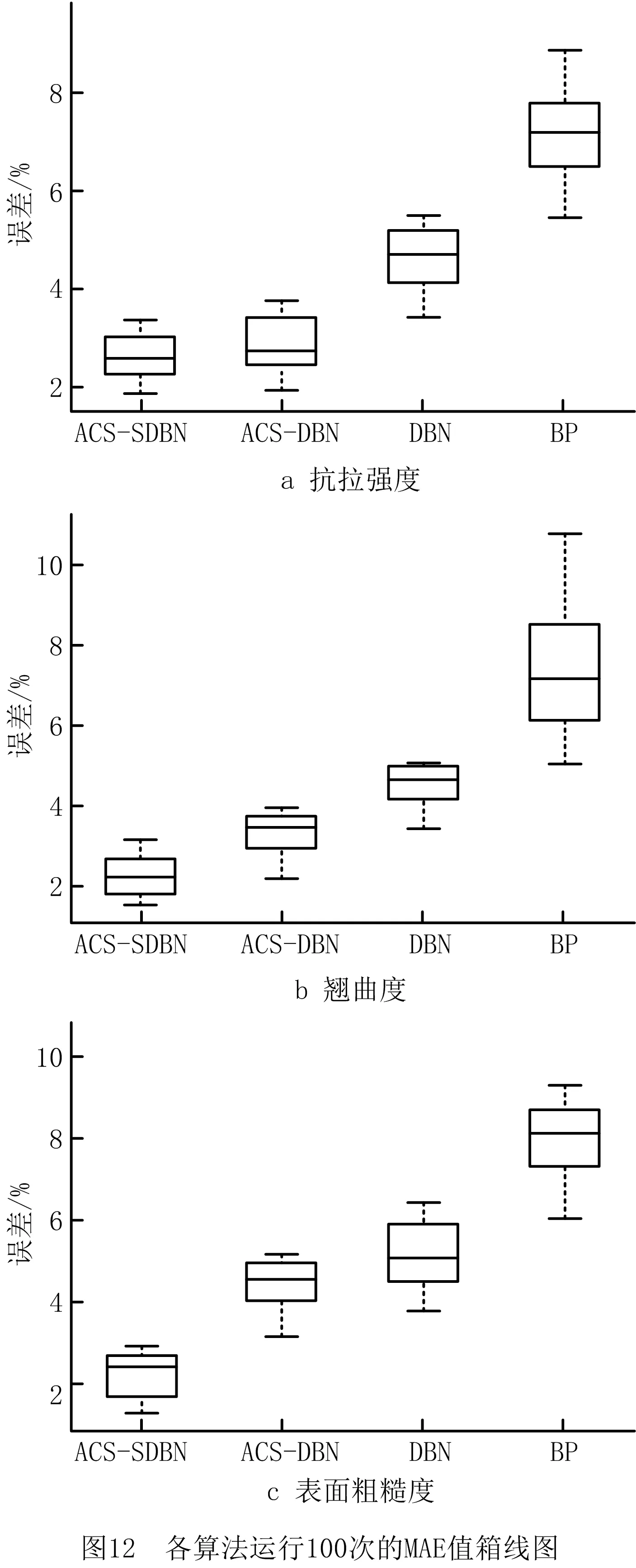
750组试验样本在不同模型下的实际值与预测值对比曲线如图9～图11所示。由图可知，与ACS-DBN、DBN、和BP相比，GS-ACS-SDBN模型预测值的变化趋势与真实值基本一致，曲线重叠程度最高，验证了ACS-SDBN模型在预测完全填充型FDM零件抗拉强度、翘曲度和表面粗糙度方面的有效性和优越性为避免预测结果偶然性问题，基于实验数据，对ACS-SDBN，ACS-DBN，DBN和BP模型运行100次，抗拉强度、翘曲度和表面粗糙度的平均相对百分比误差MAPE的箱形图统计结果如图12所示。图中ACS-SDBN模型下抗拉强度的误差范围为[1.86%,3.36%],翘曲度的误差范围为[1.52%，3.17%],表面粗糙度的误差范围为[1.28%，2.96%]，这3个质量特性的平均误差百分比范围和和均值都小于ACS-DBN，DBN和BP的预测误差。上述结果充分显示了基于ACS算法优化的SDBN模型可以获得比其他3种模型更好的非线性逼近效果，在提高模型精度，即减小模型预测误差的同时也提升了模型预测的稳定性，进一步验证了ACS-SDBN模型应用于完全填充型FDM零件质量预测中的优越性。

4 结束语

针对FDM零件质量与各工艺参数之间呈现的复杂非线性关系，导致传统方法难以准确预测的问题，本文提出一种基于ACS算法的SDBN质量预测模型，实现了多工艺参数影响下完全填充型FDM零件抗拉强度、翘曲度和表面粗糙度等质量特性的数字化预测。

(1)利用相关性分析方法(RVmod)确定影响完全填充型FDM零件质量特性的关键影响因子为切片厚度、挤出速度、喷头温度、成型室温。

(2)基于SDBN模型构建完全填充型FDM零件质量预测模型，采用网格搜索和交叉验证确定模型的最优超参数组合，利用ACS算法优化网络学习参数，从而进一步降低模型的误差。相较于优化前的SDBN模型，基于ACS算法优化后的SDBN模型获得的训练误差更小，网络训练精度得到显著提升。

(3)基于交叉验证和测试集评估模型性能，结果表明，与ACS-DBN、DBN和BP相比，本文设计的ACS-SDBN模型能更有效地映射FDM零件质量特征与工艺参数之间复杂的非线性关系，模型交叉验证的验证准确率可达95.86%以上，预测准确率可达96.94%以上，模型具有较高的精度和稳定性。