多项式曲线优化的垂直泊车路径规划与跟踪

江铭，彭育辉，黄炜，，徐德强

(1. 福州大学机械工程及自动化学院，福建 福州 350108; 2. 厦门金龙旅行车有限公司，福建 厦门 361006)

0 引言

自动泊车技术不仅能有效改善交通状况避免泊车事故的发生，还能提高泊车成功率，减轻驾驶员的泊车压力，现已成为智能驾驶领域研究的重点内容[1]. 现有主要的自动泊车路径规划和跟踪策略可分两种，一是通过分析泊车过程中的环境数据和对应驾驶员控制信息，应用模糊逻辑学和神经网络理论反复学习泊车路径并转化为复杂的转向策略实现自动泊车. 但此类方法需制定模糊规则和调节控制参数，涉及大量经验数据，且适应性差无法应对陌生泊车环境[2]； 二是根据汽车运动学限制和空间约束预先规划出泊车过程路径，通过追踪算法实现泊车，此类方法具有较强工程实践意义[3]. Glaser等[4]、 Song等[5]、 黄江等[6]、 张家旭等[7]分别采用直线-圆弧、 B样条、 多项式曲线、 回旋曲线方法设计泊车路径. 在提高路径跟踪精度方面，主要方法有PID控制[8]、 滑模控制[9]、 模型预测控制[10]、 模糊控制[11]等. 李茂月等[12]通过前向行驶过程修正待泊汽车与停车位之前的位姿关系，保证了泊车过程的安全性及避免进入泊车死区，但所规划路径曲率不连续. 张家旭等[13]通过高斯伪谱法求解泊车路径规划的最优控制问题得到无碰撞泊车路径，扩大了泊车场景的应用. 此外，赵林峰[14]基于反正切函数拟合泊车路径，设计非时间参考路径跟踪控制模型，同时应用自抗扰控制策略设计了转向控制器，实现对汽车转角的跟踪.

垂直泊车作为自动泊车系统广泛使用的场景，当前垂直泊车路径规划系统研究主要基于单步后退的规划方法. 由于单步后退泊车存在无中间段姿态调整措施和出现大幅度原地转向的局限，在很多场景下都无法直接通过单步后退泊车方法实现自动泊车，因此研究双步进退的垂直泊车路径规划方法显得尤为重要. 上述研究仍存在规划路径曲率不连续、 计算量较大和对汽车线控转向系统要求高等问题，本研究基于多项式曲线优化，对双步进退垂直场景下的泊车路径规划与跟踪方法进行研究. 构建车辆在行驶过程中的运动学模型，分析其可行起始点范围，并综合考虑车辆位姿、 结构和道路边界约束，以多项式为基函数、 泊车终点姿态角最小为目标，建立泊车多约束非线性函数规划模型. 同时，利用带罚函数的粒子群算法求解满足曲率平滑的无碰撞泊车路径，设计模糊神经网络控制器进行路径跟踪. 在Simulink/Carsim联合仿真平台上对所提的泊车路径规划算法和跟踪控制策略进行仿真测试分析.

1 泊车可行起始点范围

双步进退垂直泊车示意如图1(a)所示. 双步进退垂直泊车工况下，车辆从起点T0到终点T4的泊车过程如图1(b)所示.泊车过程可分为4个阶段： 1)从起点T0沿直线段L1行驶到T1； 2)以点E1为圆心，R1为半径，从T1行驶θ1角度到T2； 3)以点E2为圆心，R2为半径，从T2行驶θ2角度到T3； 4)从T3行驶L2距离到终点T4.

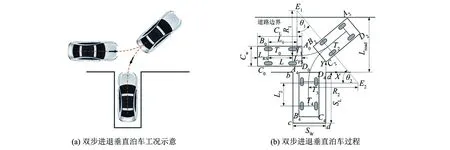
图1 双步进退垂直泊车

考虑汽车最小转弯半径约束和泊车空间避障条件，基于直线-圆弧路径下计算垂直泊车可行起始点范围.

泊车空间避障约束包括： 1) 车辆右后点C与车位边界的碰撞约束，即车辆中轴点与右方道路边界的距离应大于极限值LK； 2) 车辆左前点A与道路边界的碰撞约束，即T1-T2路径下车辆左前点A纵坐标的最大值应小于道路宽度Lroad; 3) 车辆左后方与车位点b的碰撞约束，即T2-T3路径下车辆左后点B在坐标轴上的横轴坐标值大于-SW； 4) 车辆右后方与车位点a的碰撞约束，即T2-T3路径下车辆右侧方到车位点a的距离大于极限值.各几何约束如下所示：

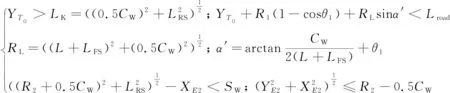
(1)

式中：CW为汽车宽度；L为汽车轴距；LFS为汽车前悬长度；LRS为汽车后悬长度；Rmin为汽车后轴中点的最小转弯半径；SW为泊车位宽度；YT0为泊车起始位置时汽车后轴中点纵轴坐标值；XE2、YE2分别为点E2横纵轴坐标值.

考虑最小转弯半径约束以及直线段长度限制，可得：

R1≥Rmin;R2≥Rmin;L1≥0;L2≥0; 0<θ1<π; 0<θ2<π

(2)

综上所述，双步进退垂直泊车可行起始点范围是由式(1)和式(2)的约束条件共同组成的封闭区域. 利用Matlab求解，可得双步进退垂直泊车可行起始点范围.

2 垂直泊车路径规划

垂直泊车路径规划问题可描述为： 待泊车辆在起始位置和终止位置间寻找不超过车辆转向极限及曲率连续平滑的曲线段，且沿该线段行驶时车辆不与道路边界发生碰撞. 将双步进退垂直泊车过程模型化，寻找合适曲线为路径基函数. 经过比较发现，垂直泊车曲线类似C型曲线，与反正切、 B样条、 回旋和多项式曲线相似，但反正切曲线函数在路径起始点不能满足曲率为零或小曲率的要求，B样条曲线函数和回旋曲线函数在求解过程中规划参数较多，计算量较大且无法准确地确定控制节点的数量和位置，而多项式曲线函数既能保证泊车路径的曲率为连续变化，不存在车辆大幅度原地转向的情况，又能减少求解规划参数降低计算量. 因此本研究选取多项式曲线函数为路径基函数，停车姿态角最小为目标，建立多约束非线性模型，并应用改进的基于罚函数粒子群算法进行求解. 垂直泊车路径规划问题可描述为：

min|θend|; s.t.(车辆位置约束; 汽车结构几何约束; 空间避障约束)

(3)

2.1 双步进退垂直泊车规划路径约束

2.1.1车辆位置约束

双步进退垂直泊车过程如图1(b)所示，假设T1-T2和T2-T3过程汽车行驶路线表达式分别为：

Y=P1X4+P2X3+P3X2+P4X+P5；U=V1X4+V2X3+V3X2+V4X+V5

(4)

式中：P1～P5以及V1～V5为待求多项式参数；Y为汽车T1-T2段前进曲线函数；U为汽车T2-T3段后退曲线函数.

汽车行驶路径需经过起始位置点T1、 经停位置点T2和终止位置T3，故建立如下约束表达：

(5)

且多项式曲线在起始位置点、 经停位置点和终止位置点的导数已知，可建立如下约束：

(6)

2.1.2汽车结构几何约束

汽车沿路径曲线行驶时受自身结构限制，所以转向角不超过一定范围值，约束表达如下：

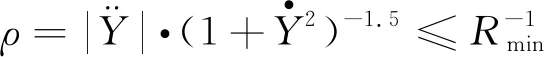
(7)

式中:ρ为泊车路径曲率.

2.1.3空间避障约束

为保证泊车过程中车辆不与周围固定障碍物发生碰撞，车辆的路径函数需满足以下要求.

1) 由图2(a)可知，为避免行驶车辆的左前端点A和车辆左后端点B与道路边界的碰撞，要求车辆端点A纵坐标YA和车辆端点B纵坐标YB的最大值应小于道路宽度Lroad，即：

(8)

2) 由图2(b)可知，为避免行驶车辆的右侧轮廓与待泊车位右侧a点发生碰撞，要求车辆轮廓线BC位于车位点a的上方，即：

(9)

3) 由图2(c)可知，为避免行驶车辆的左后轮廓与待泊车位的左侧发生碰撞，要求车辆端点B横坐标值XB应大于-SW，即：

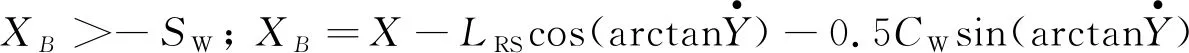
(10)

2.1.4目标函数

在双步进退垂直泊车多约束非线性函数模型中，选择停车姿态角最小为目标函数，即双步进退垂直泊车过程目标函数为：

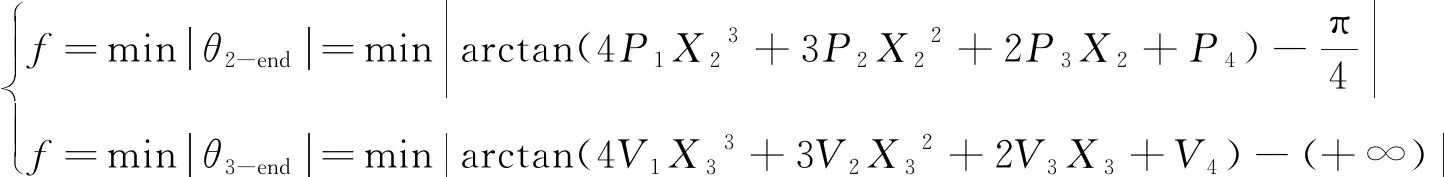
(11)

2.2 基于罚函数粒子群算法求解路径

粒子群算法是一种基于群集协同的随机搜索算法，该算法主要通过群集中各单独体内的相关协助和资讯共享来筛选可行解[15]. 标准粒子群算法主要用于求解无约束的数学模型，考虑到本研究规划路径函数中的约束条件较多，包括： 车辆位置和结构约束、 空间避障约束，其求解过程较为复杂. 因此，选用带罚函数的粒子算法对该类问题进行求解，将原本的带约束限制的求解过程转化为无约束限制求解，得到满足各约束且目标函数最小的多项式曲线中未知参数，其中所确定的目标函数为： 停车姿态和车位垂直方向的夹角最小. 基于罚函数的粒子群算法流程如图3所示.

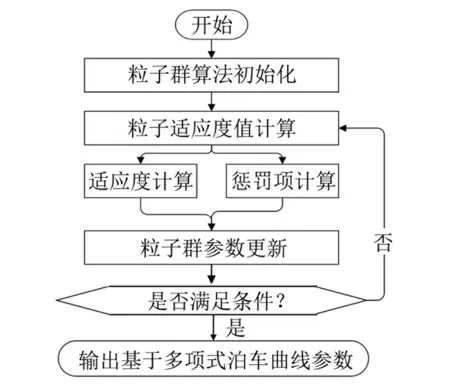
图3 粒子群算法求解流程

3 垂直泊车路径跟踪控制

泊车路径跟踪控制的核心是通过控制车辆的转向轮转角，使汽车后轴中心点和航向角能稳定快速地趋近于目标路径点和期望航向角. 为更好模拟分析路径规划结果，本研究利用模糊神经网络跟踪控制方法设计路径跟踪控制器进行泊车过程跟踪.

3.1 车辆运动学模型

将待泊汽车视为平面刚体且忽略行驶过程中的侧滑现象，选择汽车后轴中点作为参考点，建立汽车的运动学方程用于描述垂直泊车过程中汽车的转向角度、 速度与后轮中心坐标点间的关系：

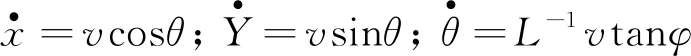
(12)

式中：φ为等效前轮转角；θ为车身航向角.

3.2 基于模糊神经网络跟踪控制器的设计

基于T-S型模糊神经网络的跟踪控制算法框架如图4所示. 利用车辆运动学模型得到当前的位置坐标点和航向角度，通过与期望轨迹进行对比，求解规划路径与实际路径的位置距离误差ye和航向角度误差θe. 将位姿误差信息输入到模糊控制器输入层中. 输入层参数的模糊子集划分成{负大 负小 零 正小 正大}，输出层为前轮转向角度φ. 模糊神经网络通过学习输入参数，包括： 位置距离偏差、 航向角度偏差与输出参数车辆前轮转向角度的关系，训练模糊隶属度函数的最佳参数，结果如图5所示.

图4 跟踪控制框图

图5 模糊神经网络训练结果

4 仿真分析

自动泊车的场景和单步垂直泊车仿真模拟如图6所示.

图6 泊车场景及单步垂直泊车工况

复杂的自动泊车场景如图6(a)所示，场景中车道宽度为5.5 m，垂直泊车位尺寸为5.0 m × 2.3 m. 图中空闲垂直泊车位为目标车位，道路前方为车库墙体. 在该泊车环境下，待泊车辆无法直接通过单步倒退垂直泊车的方式驶入目标车位. 单步倒退垂直泊车过程如图6(b)所示, 基于逆向最小转弯半径的泊车方法模拟单步垂直泊车过程如图6(c)所示. 待泊车辆从目标车位起点出发，到达终点位置时会与车库墙体碰撞，且在泊车过程中会与车道边界线发生重叠.

为实现在该泊车环境下的泊车入库，利用Simulink/CarSim联合仿真对所提双步进退垂直方法进行分析. 首先在Simulink中搭建基于罚函数粒子群的路径规划模块和基于模糊神经网络控制的路径跟踪控制模块，并导入含有泊车场景和车辆模型的Carsim模块. 汽车主要参数包括： 汽车长度CL为4.453 m; 汽车宽度CW为1.683 m； 最小转弯半径Rmin为4.2 m; 汽车轴距L为2.676 m; 汽车前悬长度LFS为0.721 m; 汽车后悬长度LRS为1.056 m. 双步进退垂直泊车规划控制结果如图7、 8所示，所分析可行起始点范围如图9所示.

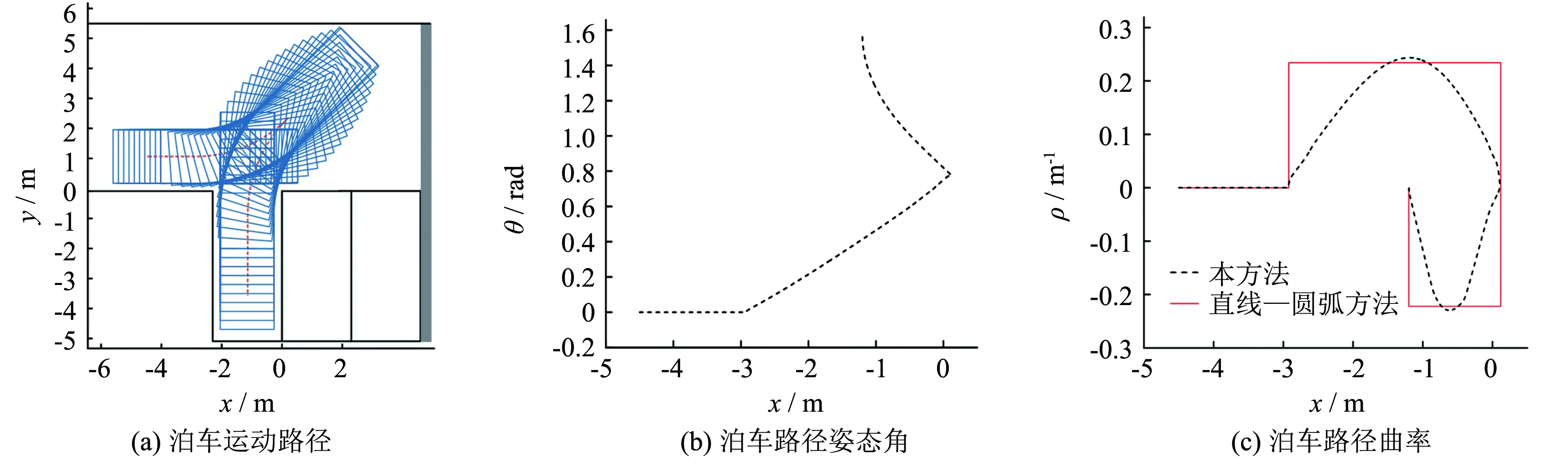
图7 垂直泊车路径规划仿真结果

图8 垂直泊车路径跟踪仿真结果

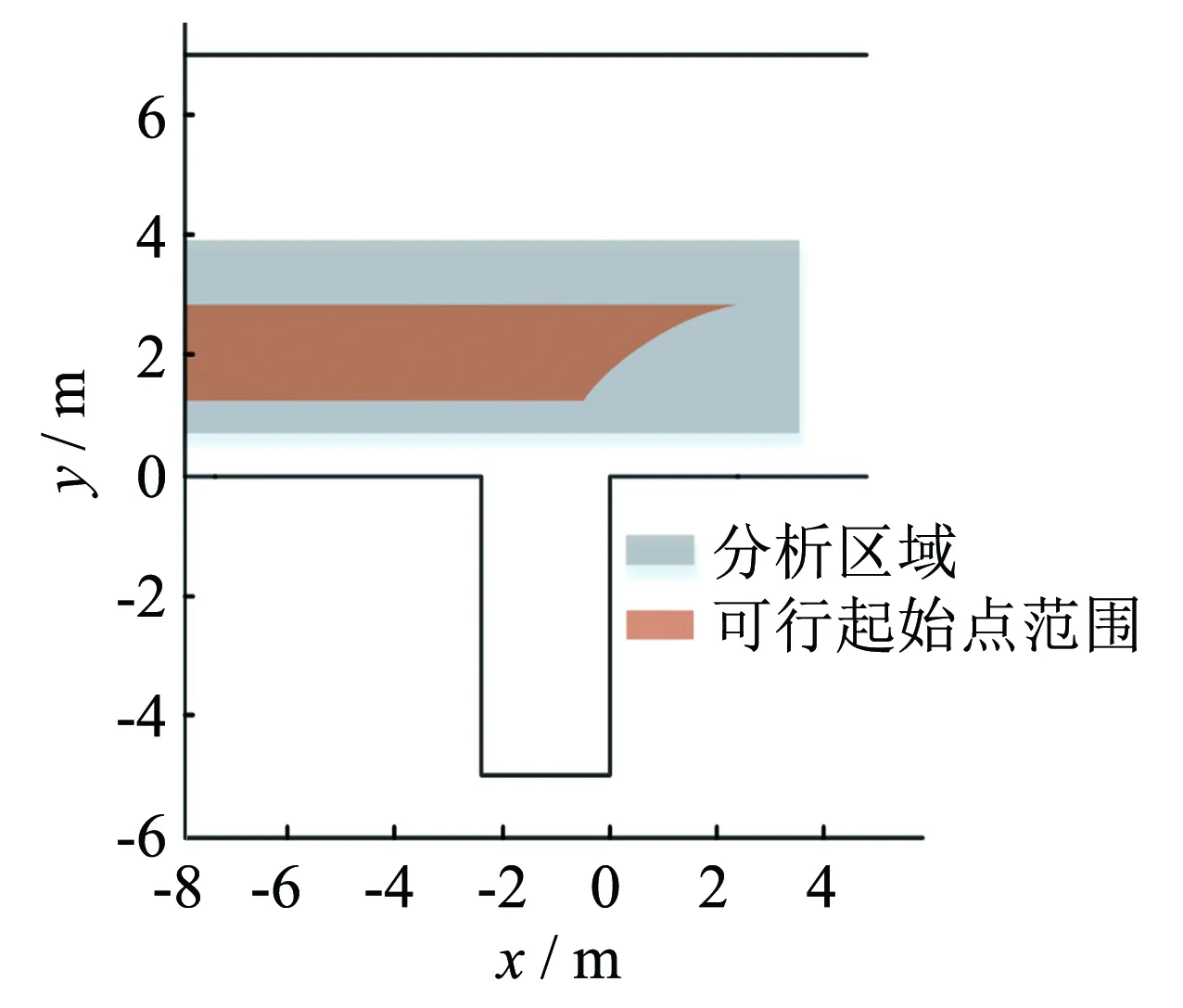
图9 可行起始点范围

图7(a)采用罚函数粒子群算法得到多步垂直泊车路径, 引导车辆由起始位置泊到车位内，且在泊车过程车辆外轮廓包络未与车位和道路边界发生相交. 由图7(b)和图7(c)中传统直线-圆弧规划方法与本方法所得到泊车路径的姿态角和曲率对比可知： 虽然两种方法得到的泊车路径曲率为-0.238～0.238 m-1，满足汽车转向结构约束条件，但采用直线-圆弧方法进行泊车路径规划，在直线段与圆弧段的交汇处会出现曲率突变的情况，汽车需进行较大幅度的原地转向; 而采用本算法所得曲率连续且平滑, 在曲率极大值和极小值之间有过度曲线无突变点，能够避免在路径跟踪过程中因曲率突变带来的误差. 由图8所示，采用基于模糊神经网络方法的路径跟踪控制器，在行驶过程中使待泊汽车后轴中心点的行驶路径航向角贴合所规划路径最终泊车停车位. 泊车过程中，最大位置跟踪误差小于0.08 m，最大位姿角跟踪误差小于3°，满足路径跟踪精度. 从而验证所提双步进退垂直泊车路径规划和跟踪策略的有效性.

5 结语

针对垂直泊车路径规划问题，提出一种基于多项式曲线的双步进退路径规划方法. 综合考虑汽车位置约束、 结构约束和道路边界约束，以多项式为基函数、 泊车终点姿态角最小为目标，通过求解多约束非线性函数模型获得规划路径. 通过路径规划跟踪的计算机仿真，结果表明, 所提的泊车路径规划策略能获得曲率平滑连续的路径，并有效规避碰撞，是一种有效的垂直泊车路径规划方法.