基于矩阵型惯性投影神经网络的非负矩阵分解算法
李小玲,夏又生
(福州大学数学与统计学院,福建福州 350108)
0 引言
非负矩阵分解(nonnegative matrix factorization,NMF)是一种有效的特征学习技术,旨在将一个高维的非负矩阵分解为两个低秩非负矩阵的乘积,可以有效地进行数据降维,并得到基于部分的表示.
Paatero等[1]最先引入正矩阵分解这一思想. 在NMF的求解算法,乘法更新算法[2]易于实现,但无法保证收敛到驻点[3]. 为了解决上述缺陷,Berry等[4]提出了交替非负最小二乘法(ALS). 而后,Lin[5]提出了投影梯度法,大大提高了交替非负最小二乘法的收敛速度. 基于NMF的基本模型,众多改进的 NMF 算法[6-8]也相继被提出,其中Li 等[6]提出局部NMF用于人脸检测,Hoyer[7]将稀疏编码的思想融入到NMF中,Cai等[8]提出的图正则化非负矩阵分解(graph regularized NMF,GNMF)可以将数据的内在结构嵌入低维表示.
作为一种并行优化方法,神经动力学优化方法在处理优化问题中展现出优越的搜索能力. Li等[9]解决了一类矩阵不等式约束矩阵的最小二乘问题形式; Huang等[10]提出了求解矩阵值优化问题的连续时间和离散时间两种矩阵型投影神经网络; Ye等[11]提出了一种求解盒约束条件下矩阵变量非线性优化问题的矩阵型神经动力学方法. 在Dai等[12]的向量模型的基础上,本研究提出一个基于连续时间矩阵型惯性投影神经网络的NMF算法,并将其运用到人脸识别. 理论分析说明基于矩阵型神经网络的交替迭代算法能够收敛到矩阵非负分解优化问题的偏最优解. 比较4种基于常见的非负矩阵分解算法,计算结果验证了所提出算法的有效性.
1 非负矩阵分解
V≈WH
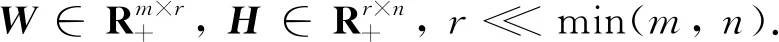
基于NMF模型,Cai等[8]提出了图正则化非负矩阵分解方法,目的是有效表示数据的内在结构,为了加强稀疏性,Dai等[12]引入了稀疏正则化模型. 稀疏图正则化NMF优化模型为:
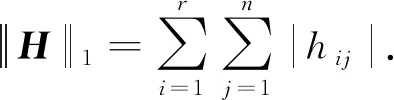
由于问题(I)是一个双凸优化模型[13-14],为了求解问题(I),将其分解为如下两个凸优化子问题:
2 矩阵型神经网络
2.1 惯性投影神经网络模型
为了解决优化问题(Ⅱ),Dai等[12]提出一个向量型惯性投影神经网络模型. 为了加速和并行化,提出一种矩阵型惯性投影神经网络(matrix inertial projection neural network,Matrix-IPNN), 即:
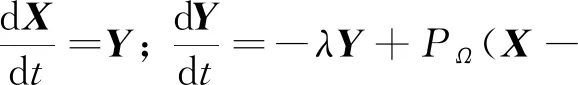
(1)
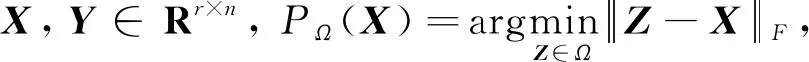
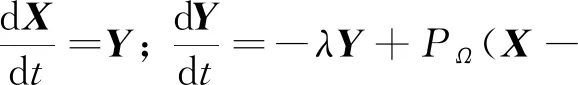
(2)
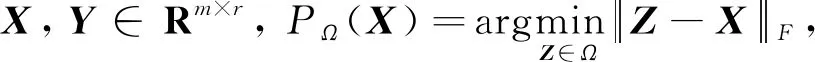
2.2 稳定性分析
由于网络(1)和(2)结构相似,所以不失一般性,针对网络(1)给出稳定性分析.
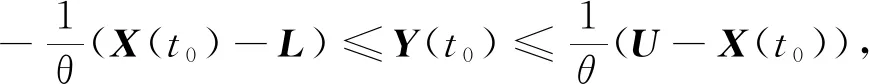
证明 首先考虑X≥L,即证明X-L≥0,记Z=X-L,则式(1)可变换为:
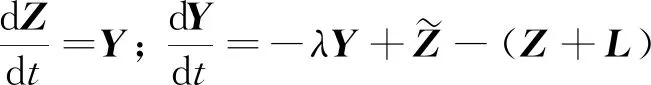
(3)
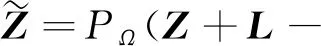
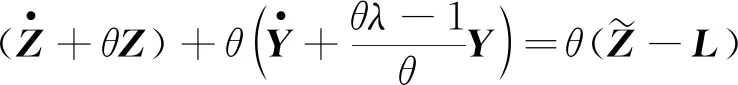
(4)

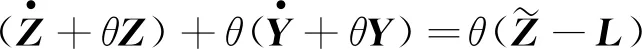
(5)
式(5)两边同时乘以eθt并积分,可得:
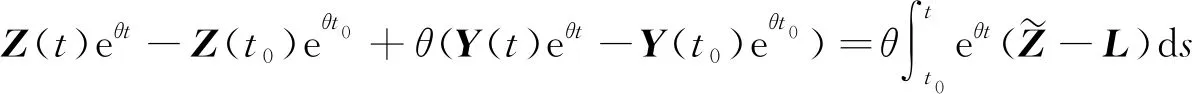
(6)
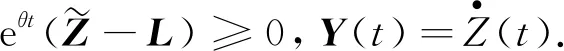

(7)
式(7)两边同时除以θ,整理得:
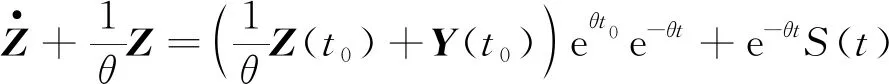
(8)
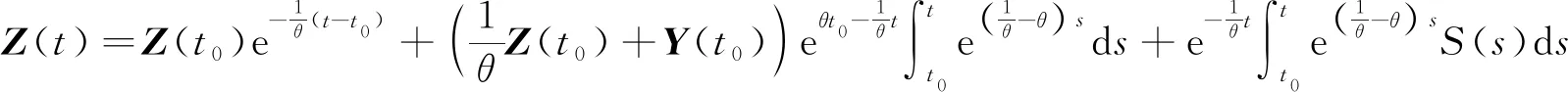
(9)
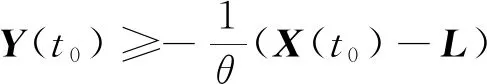
定理1定义N(X)=X-PΩ(X-∇f(X)),如果满足下列两个条件.
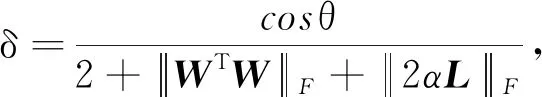
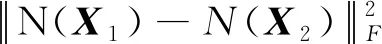
其中:θ是N(X1)-N(X2)和X1-X2的夹角.
2)δλ2>1.则式(1)的状态解将全局收敛到问题(Ⅱ)的最优解.
证明 首先证明, 式(1)的状态解X(t)有界.考虑X*∈Ω,定义李雅普诺夫函数:
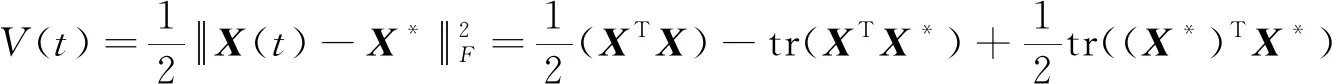
(10)
对式子(10)关于t求一阶导,有:
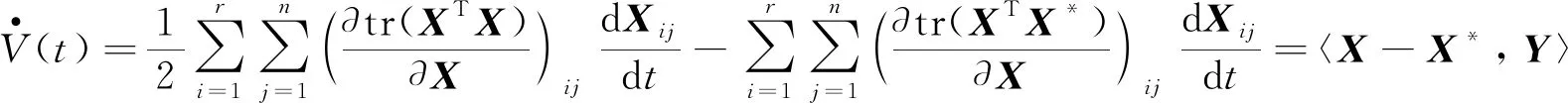
(11)
同理可得V(t)关于t的二阶导为:
(12)
将式(11)和式(12)加权求和,由N(X)=X-PΩ(X-∇f(X)),有:
为了更直观的表现小学生口算速度发展的趋势,以年级为横坐标,广度为纵坐标,对4种口算(不进位加法、进位加法、不退位减法、退位减法)广度的发展趋势折线图进行分析,具体如图2所示.
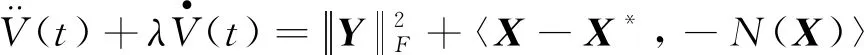
(13)
已知N(X*)=0,根据式(13)和条件(a)可得:
因此有:
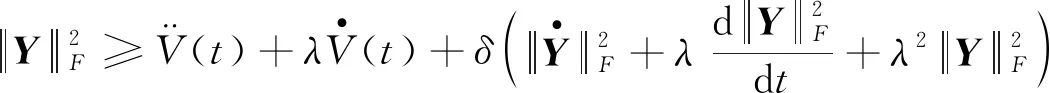
(14)
式(14)可改写为:
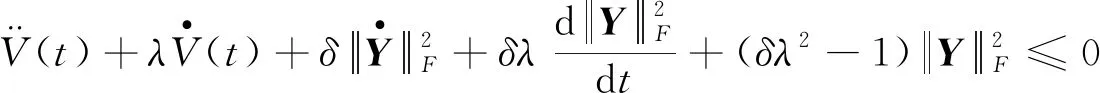
(15)
这表明函数:
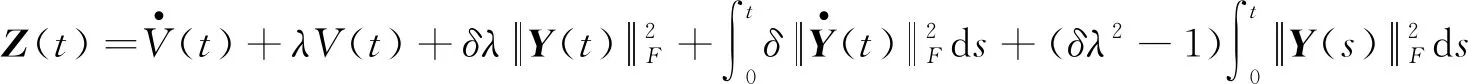
(16)
单调非增. 因此,对任意t>0,有:
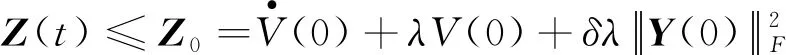
(17)
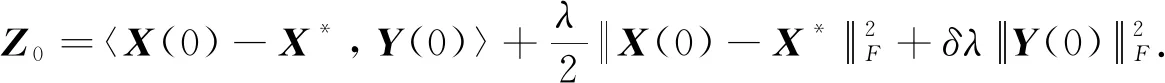
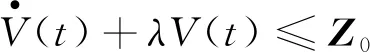
(18)
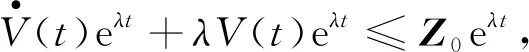
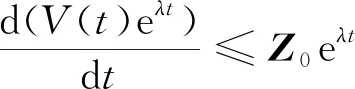
(19)
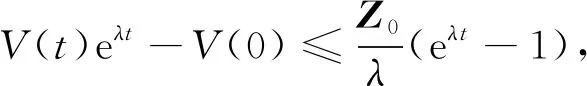
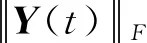
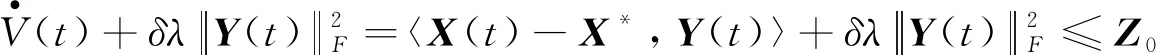
(20)

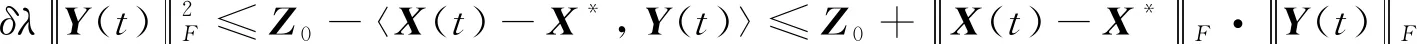
(21)
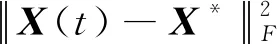
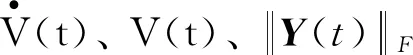
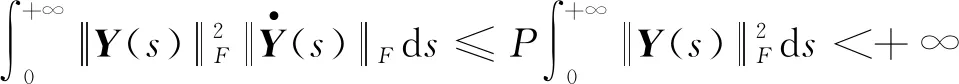
(22)

根据无穷积分的比较判别法和式(22),有:
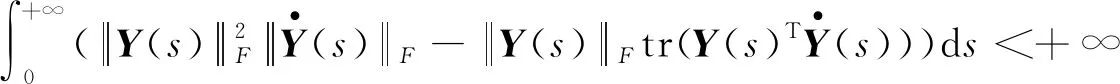
(23)
根据无穷级数的性质,以及式(22)~(23)可得:
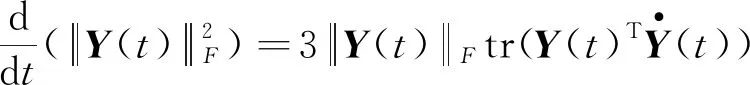

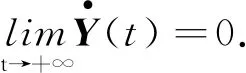
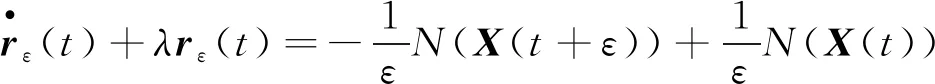
(24)
由条件1)可得:
备注: 在定理1中,条件1)可满足.接下来讨论参数δ的存在性.对任意X1和X2,有:
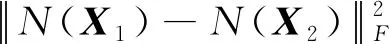
根据欧拉离散化,式(1)可改写为如下差分形式:
Xi+1=Xi+hXi;Yi+1=Yi+h(-λYi+PΩ(Xi-∇f1(Xi))-Xi)
(25)
根据定理1的结果和数值ODE理论[15],当h足够小时,算法(25)将收敛于(Ⅱ)的最优解.
3 非负矩阵分解算法
3.1 交替迭代算法描述
基于Matrix-IPNN,提出一个求解稀疏图正则化NMF问题的交替迭代算法.

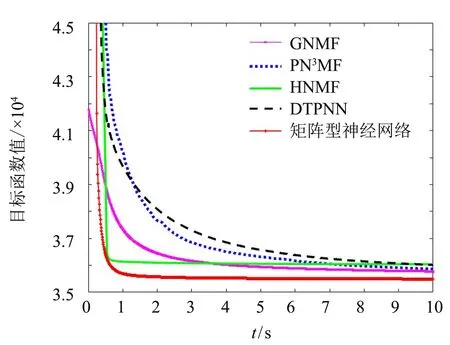
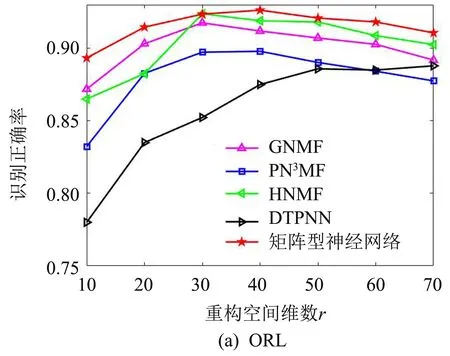
算法1 基于Matrix-IPNN交替迭代优化稀疏图正则化非负矩阵分解问题Output: W*∈Rm×r+, H*∈Rr×n+while iter 在问题(I)中约束是无界的,但可以很容易地给变量W和H加上一个较大的上界.此外,由于在一般情况下r< 定理2在问题(Ⅰ)中,为W和H增设上界UW和UH,并设W列满秩和H行满秩,则: 1) {(Wk,Hk)}至少存在一个聚点; 2) {(Wk,Hk)}的所有聚点都是偏最优解,且其目标函数值相同. 证明 首先,根据引理1可得0≤Wk≤UW及0≤Hk≤UH,因此序列{(Wk,Hk)}包含在一个紧集内.其次,子问题(Ⅱ)和问题(Ⅲ)可分别转化为如下二次规划的形式: 由W列满秩和H行满秩知WTW和HHT是正定的.结合L是半正定矩阵[16]可知,问题(Ⅱ)和(Ⅲ)是严格凸规划,即问题(Ⅱ)和(Ⅲ)都有唯一解.根据文献[13]的定理4.9可得结论. 根据双凸综述文献的定理4.1[13],可知问题(Ⅰ)的偏最优解也是问题(Ⅰ)的驻点. 为验证该算法有效性,与利用投影神经网络求解非负矩阵分解算法(PN3MF)[14]、 图正则化非负矩阵分解算法(GNMF)[8]、 混合非负矩阵分解算法(HNMF)[17]、 离散神经动力学算法(DTPNN)[18]等4种NMF算法进行比较. 各算法的计算复杂度见表1. 表1 各算法的计算复杂度 表1中PN3MF复杂度中的t表示每次找步长时做Armijo不等式判断的平均次数. Matrix-IPNN含有内循环,复杂度中的K表示内循环的次数. 这里主要讨论上述5种算法在30 s内的收敛速度. 矩阵V、W和H都是随机生成的,介于0和1之间的数. 令m=1 000,n=1 000,r=50,h=0.05,K=1 000,max_iter=3 000,α=0,β=0和λ=20,图1展示了运行时间跟目标函数的关系. 根据图1可知,在有限的时间内Matrix-IPNN的目标函数比其他几个算法下降得更快. 图1 收敛速度比较 为说明所提的矩阵型惯性投影神经网络在人脸识别问题上的有效性,在不同的数据集上进行数值实验,并给出详细的实验结果. 4.2.1数据集 本实验使用两个公开人脸图像数据集: ORL数据集和Yale数据集. 数据集详情如下: 1) ORL数据集. 包含40个人共400张灰度图像, 每个人有10张图像,尺寸为112 px×92 px. 2) Yale数据集. 包含15个人共165张灰度图像, 每人11张图像,尺寸为64 px×64 px. 图2~3分别展示了ORL与Yale 数据集的部分人脸样本. 在实验中,对两个数据集都进行随机划分,将每个人的4张灰度图像用于训练,其余图像用于测试. 图2 ORL数据集示例图像 图3 Yale数据集示例图像 4.2.2识别结果 假设B是测试集中图像的总数,B1是被正确识别的图像的数量,识别正确率[19]定义如下: 图4的子图(a)和(b)分别展示了各算法在ORL和Yale上的识别正确率随着重构空间维数r的变化.对于每个给定的r,在随机划分的训练集和测试集上执行20次训练及测试. 实验中Matrix-IPNN的参数设置为h=0.05,K=1 000,max_iter=3 000,α=10,β=1,λ=20和ε=e-5. 图4 ORL和Yale上各算法识别正确率的变化趋势 在实验中,Matrix-IPNN算法的识别正确率始终可以保持较高水平. 实验结果说明Matrix-IPNN算法在人脸识别问题中是有效的. 本研究通过扩展向量型IPNN提出矩阵型IPNN,证明了矩阵型IPNN的稳定性. 进而提出基于矩阵型IPNN交替迭代求解NMF问题的算法,分析了时间复杂度和收敛性,将其应用于人脸识别. 实验结果表明,与常见的NMF算法相比,提出的算法在识别正确率和速度上有明显改进.3.2 交替迭代算法的收敛性
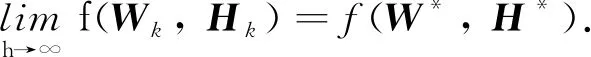
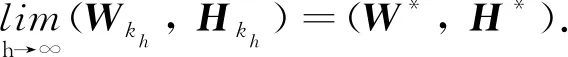
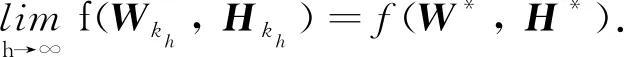
4 实验结果与分析

4.1 数值实验
4.2 非负矩阵分解算法在人脸识别的应用


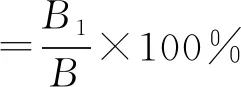
5 结语

