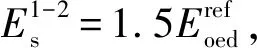湖相沉积典型软土HSS模型参数取值研究
陈赵慧, 阮永芬, 王 鹏, 朱 强, 闫 明, 蔡 龙
(1. 昆明理工大学建筑工程学院, 云南 昆明 650500;2. 中国有色金属工业昆明勘察设计研究院有限公司, 云南 昆明 650051;3. 中铁十六局集团北京轨道交通工程建设有限公司, 北京 101100;4. 中铁二十局集团第五工程有限公司, 云南 昆明 650000)
0 引言
复杂地质和环境条件下的深基坑工程,地震安全性评价时都需建模进行数值分析基坑开挖对周围环境的影响。但如何科学准确地选择土体本构模型及计算参数是数值模拟亟待解决的科学问题,也是提高数值模拟分析结果的准确度和可信度的前提[1-2]
已有的本构模型中,Mohr-Coulomb(MC)模型[1]无法模拟土体首次加-卸-再加载间的刚度差异等特性。Duncan-Chang(DC)模型[3]不能反映土体的剪胀、软化及各向异性等特性。Drucher-Parger(DP)模型[4]能同时考虑静水压力对屈服强度的影响和岩土材料的剪胀性,方法简单参数少,但也同样无法反映土体破坏前的行为。Cam-clay Model(CC)模型[5]假定土的屈服只与平均主应力和偏应力有关,与第三主应力无关。Modified Cam-Clay model(MCC)模型[6]能反映土体的剪缩,但无法反映其剪胀特性,虽考虑了黏性土破坏前的非线性和应力路径影响,但土体的抗剪强度明显偏大。基坑开挖中,坑底卸载表现出硬化特性,侧向卸荷使土体抵抗变形能力减小,刚度降低,硬化土(HS)模型[7]可模拟土体的这些性状,但没有考虑土体较小应变时的刚度变化。为了模拟Kondner[8]双曲线关系,Hardin等[9]提出了剪切与初始剪切刚度间关系,Benz[10]将这个关系用于硬化土模型中并加以修正,使硬化土模型能反映土的小应变刚度,这就是硬化土小应变模型(HSS)。HSS模型不仅考虑了土体开挖过程中产生的塑性变形和硬化,也考虑了加、卸载过程中土体应力导致的刚度变化。HSS模型是建立在HS模型的基础上,除增加了描述土体小应变特性的初始剪切模量和阈值剪应变外,其余参数与HS模型一致。
HSS模型参数繁多,获取完整参数需通过大量周期较长的试验。梁发云等[11]和王卫东等[12]在大量室内试验基础上获取了上海典型软土层的HSS模型参数,王卫东等[13]通过工程检验模型参数并作了修正。李连祥等[14]对济南地区HSS模型参数选取做了一些研究。目前,针对滇池湖相沉积的区域性软土的相关研究鲜有报道。本文通过大量的常规土工试验、固结试验、固结加载-卸载-再加载试验、三轴的UU、CU、CD试验以及刚度参数间的经验关系进行分析,最终得到湖相沉积典型软土层刚度参数的近似关系。然后对此类场地上的基坑工程建立数值分析模型,计算基坑开挖时引起的变形,对计算结果和实际监测数据进行对比分析,以验证选用的本构模型及模型参数取值的合理性和可靠性。
1 HSS模型简介
HSS模型构造是基于三轴排水加载试验下的双曲线图,如图1所示。
在图1中,qa是剪切强度的渐进值;qf是极限偏应力;Ei是初始弹性模量;E50是主加载下极限荷载所对应的割线模量。

图1 排水三轴试验下应力-应变双曲线关系Fig.1 Stress-strain hyperbolic relationship under drained triaxial test

2 昆明湖积软土部分参数确认



(1)
(2)γ0.7的确定方法
① 黏性土γ0.7的确定方法
Brinkgreve等[16]、谢东武等[17]及Vucetic 等[18]都给出了γ0.7的表达式,但Stokoe等[19]在已有研究基础上,给出了黏性土γ0.7的计算式:
γ0.7=(γ0.7)ref+5×10-6Ip(OCR)0.3
(2)
式中:Ip为塑性指数;(γ0.7)ref为Ip=0时的剪应变,可取2.0×10-4;OCR为超固结比。
把湖相沉积土层的试验指标代入式(2)得到常见土层的γ0.7如表1所列。

表1 湖相沉积常见土层的γ0.7
② 砂性土γ0.7的确定方法。
Seed等[20]试验发现,砂性土的e0对γ0.7的影响非常有限,在参考压力100 kPa下,γ0.7介于(0.6~3.0)×10-4,其变化范围不大。本文又收集了8个采用HSS模型描述黏土和砂土的有限元计算实例,得到黏土层的剪应变γ0.7介于(2.5~3.5)×10-4,砂性土的γ0.7均为2×10-4[14],与表1对比发现泥炭质土与其他土层间有较大差异,其参数离散性大。


表2 土体强度和小应变参数确定
3 固结试验研究
3.1 固结试验

试验方法:采用GZQ-1型全自动气压固结仪,加载压力分别为50、100、200、300、400 kPa。每级荷载下固结稳定标准为0.01 mm/h,双面排水。通过固结压缩试验得到的应力-应变关系图(图2)。

图2 应力-应变关系图Fig.2 Relation diagram of stress-strain
3.2 固结加载-卸载-再加载试验
3.2.1 试验方案
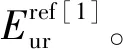

图3 4种软土的与间关系Fig.3 The relationship between of four kinds of soft soils

表3 土样物理力学性质指标

表4 加卸载试验结果
(3)
3.2.2 试验结果分析

图4 泥炭质土、黏土、粉土的与间关系曲线Fig.4 Relationship curve between of peat soil,clay soil,and silt soil
4 常规三轴剪切试验
4.1 固结排水(CD)试验
4.1.1 试验方法
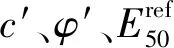

表5 土样的物理力学性质指标
4.1.2 试验结果
试验得到泥炭质土及黏土的σ1-σ3与ε1间关系如图5所示。
如在图5(a)中,泥炭质土在50及100 kPa围压下有明显峰值,产生压缩软化,而200与400 kPa围压下没有明显峰值,表现为压缩硬化。如图5(b)中,黏土只有围压为50 kPa时压缩软化,在100、200、300 kPa下都产生压缩硬化。同一围压下轴向应变达15%时,两种土剪切时对应的主应力差相差很大,黏土约为泥炭质土的两倍,表明在同一围压下,黏土的最大剪应力σ1比泥炭质土大,同时也说明泥炭质土工程性质极差。
参考压力下σ1-σ3与轴向ε1关系如图6所示。

图5 不同围压下应力-应变关系曲线图Fig.5 The relationship between stress and strain under different confining pressures

图6 参考压力下主应力差与轴向应变关系曲线图Fig.6 Relation curve between principal stress difference and axial strain under reference pressure

HS模型的基本思想是三轴加载下竖向应变ε1和偏应力q之间为双曲线关系:
(4)

(5)
根据CD试验绘制试样的有效应力摩尔圆如图8所示,得到泥炭质土与黏土的c′、φ′分别为25.1 kPa、10°和21.3 kPa、27°。
4.2 不固结不排水(UU)试验


图直线关系曲线图Fig.7 Relationship curve of straight line

表6 试样qa与Rf值

图8 土体摩尔应力圆Fig.8 Mohr's stress circle of soil

表7 UU试验土层物理力学性质指标

图9 不同围压下主应力差与轴向应变关系曲线图Fig.9 The relationship between principal stress difference and axial strain under different confining pressures
从图9中可看出,当围压为50、100及200 kPa时,土样破坏时应变ε1约为7%,在围压为400 kPa时,ε1约为9%。Δσ与ε1关系曲线大体一致,均是在ε1较小时,Δσ随ε1的增加而增加,当ε1超过一定范围时,土体产生压缩软化。


图10 参考围压下的应力-应变曲线图Fig.10 Stress-strain curve under reference confining pressure

图11 参考压力下应力-应变曲线图Fig.11 Stress-strain curve under reference pressure
5 HSS本构模型参数的确定方法

表8 典型土层之间的关系统计表

(6)
(7)


表计算结果统计表
据刘伟[25]得到第一、二及三层泥炭质土G0分别为16.3、32.6及47.7 MPa;vse分别为106.6、154.8及180.5 m/s。分析多个场地的地质勘察报告,给出第一层泥炭质土及黏土vse均小于140 m/s,本文计算得到G0为18.25 MPa与16.3 MPa相差较小,结果表明泥炭质土相对其性质而言具有较高的剪切模量,根据地质勘察告还可得到其他土层的vse。另外对昆明湖相沉积与上海海相沉积软土的HSS模型参数关系进行了对比,具体如表10所列。结果发现黏土和粉质黏土的参数都较为接近,可为昆明地区湖相沉积的黏性土研究提供参考。但由于泥炭质土的特殊性,只能通过试验或据地质勘察资料计算获取。

表10 昆明与上海地区参数对比表
5.2 破坏比Rf的确定方法
本次CD试验泥炭质土Rf大约为0.9。熊恩来[26]通过CU试验得到泥炭质土的Rf为0.95,两结果较接近,同时也表明CU试验得到的Rf稍大于CD试验的。对于砂性土和粉土层其e0小、ω低。PLAXIS手册给出所有土层均取0.9,故对三种土的Rf都取0.9。对于黏土试验结果Rf为0.5~0.7。湖相沉积区软黏土与上海、天津地区的淤泥质黏土性质较为接近[27-28],从表10可知,基于上海地区的试验结果[11]和本文试验数据综合后Rf值取0.6。据勘察结果粉质黏土的物理力学性质指标相对黏土好,故Rf为0.7。
5.3 黏性土及泥炭质土层和的确定方法

5.4 砂性土及粉土和的确定方法

图与关系曲线Fig.12 The relationship curve between

图与关系曲线Fig.13 The relationship curve between
6 工程实例验证
为验证分析结果的可靠性,选取滇池湖相沉积软土场地两个典型地铁站点基坑,根据开挖工况进行计算分析。计算参数如表11所列。

表11 地铁站点1、2基坑HSS模型参数
两车站的钢支撑都为Φ800的Q235钢材,t=16 mm,围护的地下连续墙厚都是800 mm。站点1基坑开挖深度为15 m,宽21.4 m,连续墙为C35混凝土,插入15 m深,钢筋混凝土撑采用800×1 200 mm的C30混凝土。站点2开挖深度为18.4 m,连续墙插入深度约19 m,连续墙为C30混凝土,钢筋混凝土支撑采用800×800 mm的C30混凝土,车站标准段宽为19.4 m。两个站点的支护情况、施工工序及地质情况如图14所示。采用PLAXIS 2D软件对两个基坑建模分析,采用的是HSS本构模型,计算结果和实际监测结果对比图如图15所示。

图14 站点1、2的基坑开挖工序图Fig.14 Excavation process diagram of foundation pit at subway station 1 and station 2

图15 围护结构深层水平位移计算与监测值对比Fig.15 Comparison between calculation and monitoring values of deep horizontal displacement of enclosure structure
从图15可看出,两个工程地下连续墙的深层水平位移的数值模拟与实际监测数据的变形趋势一致,站点1的计算和监测结果非常吻合,误差很小可忽略。站点2在工况3之前,计算与监测结果都非常吻合,只是在第四工况时,开挖深度12 m时计算与监测变形值基本一致,吻合较好,但12 m后,随开挖深度的增加,模拟计算与实测值出现一定的偏差,但二者变形趋势是一致的。到现场调查其原因,站点2的围护墙底是很厚的泥炭质土层,泥炭质土会产生蠕变,基坑实际开挖时支撑稍不及时就会引起基坑变形增大。通过以上计算分析知,只要选取的岩土体参数合理,就可得到可靠的模拟计算结果。同时也证明了HSS本构模型用于基坑数值模拟分析是合理的,分析结果是可靠的。
7 结论
通过大量室内试验以及收集近20个地铁站点的地质勘察报告,并结合现有研究,给出了滇池湖相沉积地区典型软土的HSS模型参数取值方法及刚度参数间的比例关系,另外针对试验结果发现泥炭质土与软黏土的力学性质差异巨大。最终研究结果可作为湖相沉积软土地区的参数取值及理论分析的依据。主要结论如下:
(1) 确定了湖相沉积软土的卸载-再加载泊松比vur、静止土压力系数K0、剪胀角ψ、小应变参数剪应变γ0.7、刚度应力水平相关幂指数m的取值方法。