基于电动汽车驱动电机振动噪声优化的转子结构设计

王晓远，罗潇宇，高 鹏

（天津大学电气自动化与信息工程学院，天津 300072）

当前正处于由传统燃油汽车向以纯电动汽车为代表的新能源汽车转变的时代，使电动汽车的数量剧增。汽车作为日常出行的主要交通工具，人们对其安静舒适性能的要求越来越高，汽车的静谧性和舒适性问题一直备受关注。电动汽车驱动电机作为汽车动力的来源，其振动噪声性能直接影响电动汽车整车的静谧性和舒适性[1]。因此，对于电动汽车驱动电机振动噪声的研究十分必要。永磁同步电机具备效率高、转矩密度高、易于控制等优势，被广泛用于驱动电机领域，但永磁同步电机功率密度高、轻量化等特点导致永磁同步电机的电磁振动噪声问题严重，因此国内外学者对永磁同步电机的振动噪声进行了大量的研究。

前苏联学者舒波夫第一次总结了永磁同步电机的振动噪声主要来源，包括：空气噪声、机械噪声和电磁振动噪声[2]。其中，电磁振动噪声是永磁同步电机振动噪声的主要来源，电磁振动噪声由作用在电机定子齿上的电磁力波产生。文献[3]推导出永磁同步电机电磁激振力波的解析表达式，分析总结了对电机振动噪声影响较大的电磁激振力波的阶次；文献[4]通过定子齿削角的方式，降低电机的振动噪声，分析了不同齿削角形状、齿削角大小对电机振动噪声的影响；文献[5]针对V型磁钢永磁同步电机提出优化隔磁桥形状的方式来降低电机的振动噪声；文献[6]提出在转子上设置三角形磁障削弱振动噪声，研究了三角形磁障尺寸对于电机振动噪声的影响，采用粒子群算法确定最优的三角形磁障尺寸。

转子分段错极和非均匀气隙这两种电机转子优化方式被广泛用于减小电机的齿槽转矩[7-8]。但关于这两种方式对电机电磁振动噪声的影响的研究相对较少。本文以一台电动汽车用永磁同步电机作为研究对象，推导出转子分段错极条件下，径向电磁力的表达式，并分析转子分段数和错极角度对径向电磁力的影响。为进一步削弱电机的振动噪声，在转子分段错极的基础上采用非均匀气隙结构进一步削弱径向电磁力，通过仿真计算确定使削弱效果最佳的偏心距值。最后，对比分析未优化、只采用转子分段错极、同时采用转子分段错极和非均匀气隙3种不同结构电机的电磁振动噪声，分析结果表明同时采用转子分段错极和非均匀气隙的电机的振动噪声最低，且对低噪声电动汽车驱动电机设计有一定的参考意义。

1 转子分段错极条件下径向电磁力分析

1.1 径向电磁力理论分析

永磁同步电机在运行过程中，电机的定子齿受到电磁力的作用产生振动噪声，与径向电磁力相比切向电磁力对电机振动噪声的贡献很小[3]，因此本文主要对径向电磁力进行分析。

图1为转子分段错极结构，其中，转子轴向分段数及每两段转子之间的错开角度会影响径向电磁力的特性。

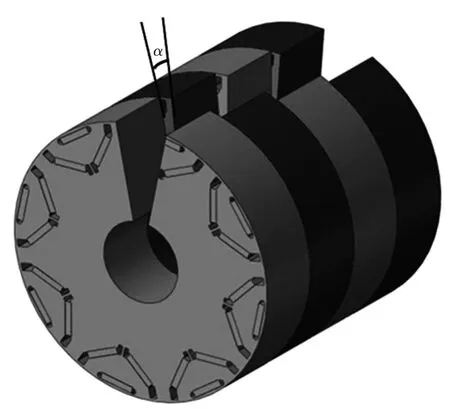
图1 转子分段错极结构Fig.1 Structure of rotor-step skewing

利用麦克斯韦张量法得到径向电磁力表达式为

式中：μ0为真空中的磁导率；Br为径向气隙磁通密度；Bt为切向气隙磁通密度；BRr为转子永磁体产生的径向气隙磁密；BSr为定子电枢电流产生的径向气隙磁密。

当定子通入三相对称电流时，定子电枢电流产生的磁动势为

式中：νS为定子电枢磁场谐波分量的次数，νS=（2r+1）p，r=0，1，2，…，+∞；为定子电枢电流产生的磁动势的νS次谐波幅值；p为极对数；θ为转子的机械角度；ω为电流的角速度；t为时间；φ为磁动势初相角。

假设分段数为n，错极角度为α。则第l段转子永磁体产生的磁动势为

式中：νR为转子永磁体励磁磁场谐波分量的次数；νR=2r+1，r=0，1，2，…，+∞；为转子永磁体产生的磁动势的νR次谐波幅值。

由于定子开槽的原因导致气隙不均匀，其等效的气隙磁导可以表示为

式中：Λ0为气隙磁导的不变分量；k为齿谐波次数，k=1，2，3，…，+∞；Λk为定子开槽引起的k阶齿谐波磁导的幅值；Z为定子开槽数。

在定子开槽影响下，定、转子径向气隙磁密分别为

将式（5）、（6）代入式（1）可得电机在转子分段错极条件下的径向电磁力表达式为

由式（7）可知，作用在定子齿表面的径向电磁力主要由永磁体励磁磁场各次谐波相互作用产生的电磁力、电枢磁场各次谐波相互作用产生的电磁力，以及永磁体励磁磁场和电枢磁场各次谐波相互作用产生的电磁力组成。

转子分段错极会影响到由永磁体励磁磁场产生的电磁力，使由永磁体励磁磁场相互作用产生的径向电磁力及永磁体励磁磁场与电枢磁场相互作用产生的电磁力沿转子轴向分别偏移相应的角度。将式（7）中永磁体励磁磁场产生的电磁力，以及永磁体励磁磁场和电枢磁场相互作用产生的电磁力化简为2个表达式为

式中：νR1、νR2分别为永磁体励磁磁场的谐波分量次数；νS1为电枢磁场的谐波分量次数；FνR1,νR2为永磁体励磁磁场产生的径向电磁力的幅值；FνR1,νS1为永磁体励磁磁场和电枢磁场相互作用产生的径向电磁力的幅值；m为转子机械角度θ前系数的简化表达式。

由式（8）、（9）可得，永磁体励磁磁场相互作用产生的径向电磁力沿轴向偏移角度为(νR1±νR2)pα(l-1)电角度；永磁体励磁磁场和电枢磁场相互作用产生的径向电磁力沿轴向偏移角度为νR1αp(l-1)电角度。

为了研究转子分段错极后电机定子齿受到的平均径向电磁力的变化，将发生相移的n段径向电磁力进行叠加求得平均径向电磁力为

由式（10）可知，分段数及错极角度的变化会影响到各个频率径向电磁力的大小。

1.2 转子分段错极参数对径向电磁力影响

为研究错极角度及转子分段数对径向电磁力的影响，对式（10）中关于错极角度和分段数的参数表达式进行分析。当 (νR1±νR2)pα和νR1αp(l-1)同时为2πN，N＝1，2，3，…，+∞时，平均径向电磁力可以表示为

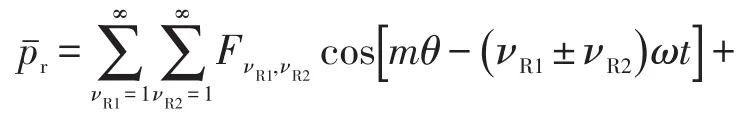
即当 (νR1±νR2)pα和νR1αp(l-1)同时为2πN电角度时，径向电磁力不受转子分段错极的影响；当(νR1±νR2)pα和νR1αp(l-1)不同时为2πN电角度时，径向电磁力受到转子分段错极的影响。

错极系数K1、K2可表示为

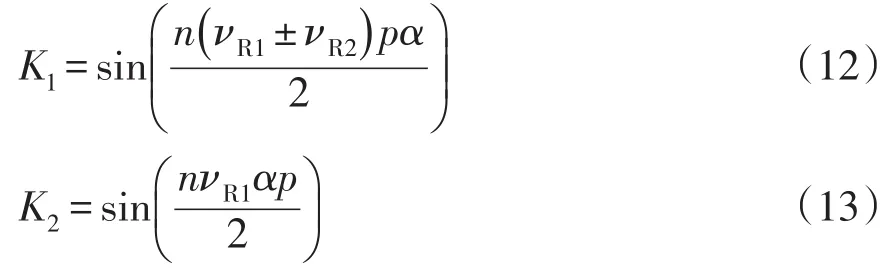
选择合适的分段数和错极角度，使K1=0或K2=0会削弱νR1±νR2次或νR1次的径向电磁力。

为验证理论分析的正确性，利用本文所研究的样机进行额定负载情况下的有限元仿真分析计算。电机各参数如表1所示，定转子截面图如图2所示。

表1 电机的主要参数Tab.1 Main parameters of motor

图2 电机截面Fig.2 Cross-section of motor

转子分段错极前后，额定转矩对比如图3所示。

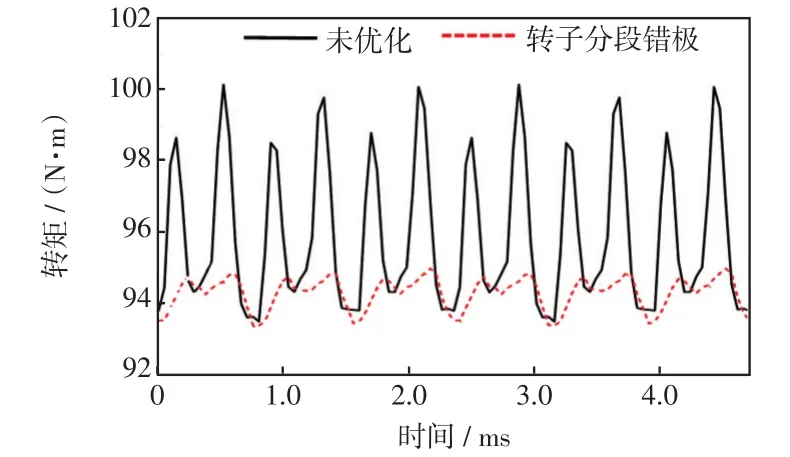
图3 额定转矩对比Fig.3 Comparison of rated torque

由图3可以看出，采用转子分段错极后额定输出转矩的平均值由95.91 N·m下降到94.32 N·m，下降幅度仅为1.66%；但转矩脉动由未优化时的6.99%下降到了1.69%，转矩脉动的下降有利于降低电机的振动噪声[9]。

图4为转子采用分段错极前后径向电磁力时间谐波分解对比。采用分段错极后除2次、4次、6次径向电磁力幅值略有增加外，8次、10次、12次、14次、16次、18次、20次的径向电磁力均有明显的下降。说明采用转子分段错极的方法可从总体上削弱径向电磁力，且转子分段错极结构对较高频率的径向电磁力削弱效果明显。

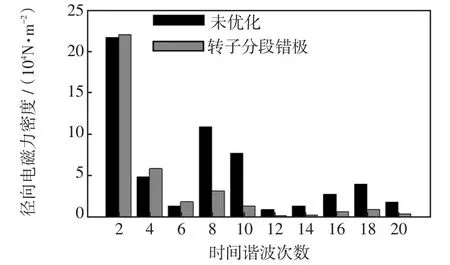
图4 径向电磁力时间谐波分解Fig.4 Time harmonic decomposition of radial electromagnetic force

2 非均匀气隙对于电机振动噪声的影响

2.1 非均匀气隙对于电磁力的影响

忽略饱和、漏磁、齿槽效应的影响，气隙磁密沿转子表面分布的表达式为

式中：Br为剩磁感应强度；hm为永磁体磁化方向的厚度；δ(θ)为气隙长度的分布函数。

由式（14）可知，通过改变电机的气隙长度沿圆周方向的分布，可改变气隙磁密沿电机圆周方向的分布，进而会改变径向电磁力，径向电磁力的变化会影响电机的电磁振动噪声。因此，通过改变气隙长度沿圆周的分布可以改变振动噪声特性。

2.2 气隙长度推导

由第2.1节的分析可知，采用转子分段错极后电机的径向电磁力明显降低。但有个别频率电磁力的幅值较大，为进一步削弱电机的径向电磁力，采用如图5所示的非均匀气隙结构优化方式。定义OO’的距离为偏心距用d表示，改变d的大小可以改变气隙长度。为研究偏心距d对气隙长度的影响，本文将推导气隙长度随偏心距d变化的表达式，推导过程用到的几何量和几何关系见图5。

图5 非均匀气隙示意Fig.5 Schematic of non-uniform air gap

气隙长度可以表示为关于d的表达式，即

对式（15）求导可得，当R＝64.9 mm，d≤10 mm时，[δ(θ,d)]＇＞0，即随着偏心距d的增加气隙长度变大，改变偏心距的大小会改变径向电磁力的特性。

为了验证非均匀气隙结构对径向电磁力的影响，选取偏心距d=5 mm，计算d=5 mm时只采用非均匀气隙及同时采用转子分段错极和非均匀气隙时的径向电磁力。将计算结果与未优化及采用转子分段错极时的计算结果进行比较，比较结果如图6所示。

图6 不同优化方式情况下电磁力谐波含量Fig.6 Harmonic content of electromagnetic force using different optimization methods

由图6可知，非均匀气隙结构可以削弱除6次谐波外的各次径向电磁力，尤其对较低频率的径向电磁力谐波削弱效果明显，但对频率较高的径向电磁力削弱效果相对较差。非均匀气隙结构对电机径向电磁力的影响和转子分段错极结构对径向电磁力的影响规律相反，同时采用转子分段错极和非均匀气隙结构可以将两者优势结合削弱全频率段的径向电磁力。

2.3 确定最优偏心距

在转子分段错极的基础上，采用非均匀气隙的方式，改变偏心距d的大小，可进一步改变径向电磁力。利用有限元仿真软件，计算偏心距d在3～10 mm范围内变化、步长为1 mm，8种情况下电机径向电磁力的时间谐波含量，通过对比分析确定削弱效果最优的偏心距值，其计算结果如图7所示。

图7 不同偏心距情况下电磁力谐波含量Fig.7 Harmonic content of electromagnetic force under different values of eccentricity

由图7可知，当偏心距d＝8 mm、d＝9 mm、d＝10 mm时，6次径向电磁力谐波幅值高于只采用分段错极时的幅值，因此最优偏心距的选择不考虑d＝8 mm、d＝9 mm、d＝10 mm；当偏心距d＝6 mm、d＝7 mm时，对径向电磁力的削弱效果最好，且效果接近。考虑到转子机械结构强度会因偏心距的增加而变差，因此选择d＝6 mm作为最优偏心距。

3 优化方案验证分析

3.1 模态分析

电机的电磁振动噪声大小不仅与电磁力的大小有关，还与电机模态特性有关。当电机的径向电磁力频率接近电机的径向模态频率时，即使该频率的径向电磁力幅值很小，也会使电机产生较大的振动噪声。因此，要对电机的径向模态进行分析，以保证电机不会发生较为严重的结构共振。

本文采用有限元分析方法对电机定子及机壳结构进行模态分析。为更加准确的计算电机在实际工作中的模态特性，在电机前端盖位置施加固定约束。电机机壳材料为铝合金，其密度为2 700 kg/m3、杨氏模量为50 GPa、泊松比为0.3；电机定子铁心为M27035，考虑电机定子铁心为硅钢片叠压结构，需要对其材料参数根据叠压系数进行等效，其等效密度为7 458 kg/m3、等效杨氏模量为198 GPa、等效泊松比为0.28。表2为电机的前5阶的径向模态振型及频率。

表2 定子及机壳结构各阶次频率及振型Tab.2 Frequency and vibration mode of each order of the stator and casing structure

由第2.3节的分析可知，电机径向电磁力波频率为偶数倍供电频率。供电频率f＝212 Hz，因此电磁力波频率主要包括2f（424 Hz）、6f（1 272 Hz）、8f（1 694 Hz）、10f（2 120 Hz）。定子及机壳结构的各阶固有频率和主要的电磁力频率均有较大差距，因此不会发生共振。

3.2 电磁振动噪声

为验证优化方法的有效性，通过仿真计算未优化、转子分段错极、同时采用非均匀气隙和转子分段错极3种结构电机额定负载时电磁振动及噪声。

谐响应分析时所加载的约束条件和模态分析保持一致，同样在电机的前端盖位置施加固定约束。图8为未优化、转子分段错极、同时采用转子分段错极和非均匀气隙这3种结构电机在额定负载时电机机壳表面的加速度频谱，该加速度频谱反映了受电磁力影响机壳表面振动的剧烈程度。

图8 振动加速度对比Fig.8 Comparison of vibration acceleration

由图8可以看出，振动加速度的峰值频率分别为424 Hz、848 Hz、1 272 Hz、1 696 Hz、2 120 Hz、2 544 Hz。这些频率点与电机供电频率的偶数倍频相对应，这是因为径向电磁力的频率为供电频率的偶数倍。当采用转子分段错极的结构后，电机的振动加速度值显著下降，由于径向电磁力在低频段削弱效果并不明显甚至略有增加，因此机壳表面的振动加速度在低频段也略有增加；当同时采用转子分段错极和非均匀气隙后，电机的振动加速度水平进一步下降，并且低频段的振动加速度值相比未优化时也有明显下降。由此可见，同时采用转子分段错极，可以显著削弱电机的电磁振动。

图9为利用有限元仿真计算得到的未优化、转子分段错极、同时采用转子分段错极和非均匀气隙3种结构电机的噪声声压级对比。

图9 声压级对比Fig.9 Comparison of sound pressure level

声压级的峰值点与机壳表面振动加速度的峰值点频率一一对应，并且机壳表面振动加速与声压级呈正相关。当采用转子分段错极后，电机最大的声压级从59.93 dB下降到54.07 dB，下降幅度为9.8%；当同时采用转子分段错极和非均匀气隙后，电机的最大声压级下降到42.66 dB，下降幅度为28.8%。同时采用转子分段错极和非均匀气隙进一步削弱电机振动噪声。

3.3 转子强度验证

由于本文对电机转子采用了非均匀气隙的结构优化方式，改变了电机转子的结构强度，因此需要对电机转子结构进行强度校核。在电机高速运行过程中，电机转子主要受离心力的作用[10]，利用有限元仿真软件计算电机在最高转速（9 000 r/min）工况下的离心力。图10为在最高转速工况下电机转子的等效应力云图。

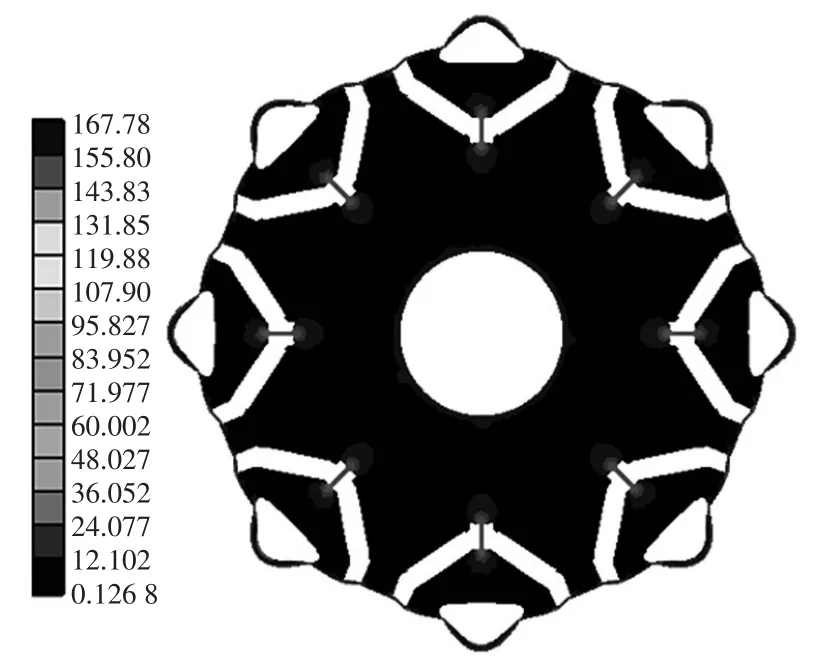
图10 转子应力分布Fig.10 Distribution of rotor stress

由转子应力分布图可得，转子的最大等效应力为167.78 MPa，转子铁心材料的屈服强度为405 MPa。转子铁心材料的屈服强度远大于电机在最高转速条件下运行时的最大等效应力。因此，优化后的转子结构机械强度满足要求。

4 样机实验

为了验证仿真分析模型的正确性，制造采用转子分段错极结构的样机。并在额定负载情况下，进行电机噪声测试实验。图11为实验测试平台。

图11 实验平台Fig.11 Experimental platform

图12为噪声测试实验得到的噪声声压曲线，由于本文在进行电机振动噪声仿真计算时，只考虑电磁力作用在电机定子齿上产生的径向辐射的噪声，没有考虑电机的机械噪声、空气动力学噪声和电机其他方向辐射的噪声，也没有考虑因电机实际制造工艺限制，可能造成的转子偏心等问题产生的噪声。因此，实验测试结果和仿真计算结果存在一定的偏差。但实验测试得到的噪声峰值点对应的频率及变化趋势与仿真计算结果基本一致，由此说明仿真分析计算模型及转子结构优化设计，可以作为电机减振降噪设计的参考。

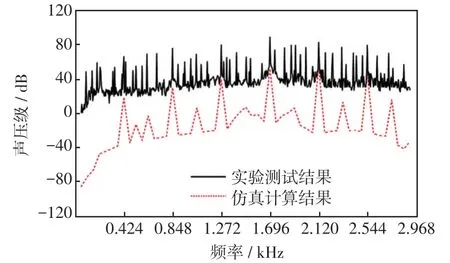
图12 噪声声压级测试结果Fig.12 Test results of noise sound pressure level

5 结语

本文以一台电动汽车驱动电机为研究对象，为削弱电机的电磁振动噪声，样机采取了转子分段错极的结构优化方式，推导出转子分段错极条件下径向电磁力的表达式，分析了转子分段错极数和错极角度对径向电磁力的影响。为进一步优化电机的电磁振动噪声，在转子分段错极的基础上采用非均匀气隙结构削弱径向电磁力，推导出气隙长度随偏心距变化的表达式，通过有限元仿真分析计算了不同偏心距条件下电磁力的谐波含量，选择出削弱径向电磁力效果最明显的偏心距值。最后通过有限元仿真分析的方法验证优化方式的有效性，并制造样机进行噪声测试实验。研究结果表明，转子分段错极的方式可以改变径向电磁力的时间谐波含量，选择合适的转子分段数及错极角度可削弱径向电磁力波，进而削弱电磁振动噪声；同时采用转子分段错极和非均匀气隙的优化方式对径向电磁力削弱效果优于只采用转子分段错极的优化方式。但偏心距的大小选择，需综合考虑电机的电磁性能与机械强度等因素。