基于致密砂岩储层气水渗流阻力系数的产能新模型
张建中 高树生 熊 伟 叶礼友刘华勋 朱文卿 杨 懿 牛文特
1. 中国科学院大学 2. 中国科学院渗流流体力学研究所 3. 中国石油勘探开发研究院
0 引言
致密砂岩气藏因其资源储量巨大且具有很大的开发潜力已成为一种重要的非常规油气资源[1-2]。致密砂岩气藏孔喉结构复杂,受见水和应力敏感的影响,其渗流规律也极为复杂[3-4]。目前使用的两相渗流方程主要是基于Muskat、Buckley和Leverett等推广的广义两相达西渗流理论体系[5]。但达西定律的这种推广只能有条件地成立[6],即相对渗透率不受渗流系统的压力和速度影响,而只是流体饱和度的单值函数(Muskat假设)。低渗透介质中气体受流速、界面因素的影响表现出的非达西渗流规律[7]并没有体现在目前通用的两相渗流方程中,导致以其为指导的产能预测结果与实际效果偏差较大[8]。因此,实现不同压力条件下的气水两相渗流模拟实验,研究致密砂岩气藏气水两相渗流特征,建立相应的渗流理论模型进行产能评价,对于高效合理开发致密砂岩气藏具有重要意义。
国内外关于气水两相渗流及其规律进行了大量研究。郭肖等[9]在实验室常温、较低压力条件下测试了12块岩样气水相对渗透率曲线,并以某高温高压井为例,模拟计算了不同温度、压力对气水相对渗透率的影响,结果表明实验温度和压力不会对水相相对渗透率曲线造成影响,而对气相相对渗透率却有很大影响。鲁瑞彬等[10]设计了不同温压条件、驱替方式、有效应力下气水相渗实验,结果表明,与地面条件相比,地层高温高压条件下气驱水时束缚水饱和度降低8%~13%,两相共渗区增加8%~15%,水驱气实验较气驱水实验相对渗透率曲线整体偏左。Ali HS等[11]探究了围压与相对渗透率的关系,当净围压升高,岩石物性变差,导致岩心束缚水饱和度增大,最终结果表现为净围压增大油相相对渗透率降低,但对水相相对渗透率无影响。
在致密砂岩气藏的研究中,气水相对渗透率实验更能直观准确地反映气水两相在微观下的流动情况[12]。Hassler[13]、Buckley 等[14]和 Rapoport等[15]分别提出了稳态与非稳态法,目前已成为实验室测定相对渗透率曲线的主要方法[16-18]。笔者在常规气水相对渗透率测试基础上进行流程改进,建立了不同压力条件下的气水两相渗流模拟实验方法。定义了表征气水两相在致密砂岩气藏储层多孔介质中流动阻力的渗流阻力系数。对比不同孔隙压力和渗透率对渗流阻力系数的影响,总结致密砂岩气藏在不同条件下气水两相的渗流规律。在实验数据的基础上,通过数学分析从系数拟合和减少参数两个角度出发建立了两个渗流阻力系数数学模型,通过Matlab数值模拟的方法验证了两个数学模型的正确性与适用性,并在两个模型的基础上推导了全新的产能方程,最后以气井实例计算了IPR曲线。
1 实验流程与方法
1.1 实验流程
改进的气水两相渗流模拟实验流程主要由供气(水)系统,储层模拟系统、采气(水)系统和数据采集系统四部分构成(图1)。为了实现高压环境下产气量的准确计量,本实验在岩样出口处放置一个10 000 mL中间容器来收集产出的气体,并通过中间容器的压力变化来换算得到实验过程中的阶段产气量。高压气水两相渗流模拟实验开始前,首先在围压为30 MPa、出口常压(0.1 MPa)的条件下开展5块岩样的纯水驱、气驱水和水驱气实验,以作对比。之后分别在30 MPa围压、10 MPa孔压,30 MPa围压、20 MPa孔压的条件下进行5块岩样的纯水驱、气驱水以及水驱气实验。
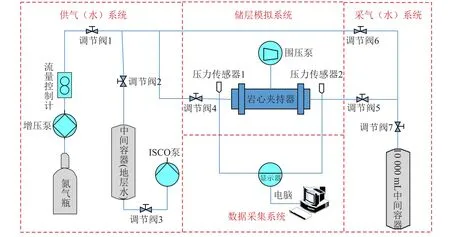
图1 高压气水两相渗流模拟实验流程图
本实验所采用的岩样是砂岩性质的露头岩样,岩样的相关基础数据如表1所示。饱和气体为99.99%的纯氮气,实验用模拟地层水是浓度为6×104ppm(1 ppm=0.000 1%)的标准盐水。
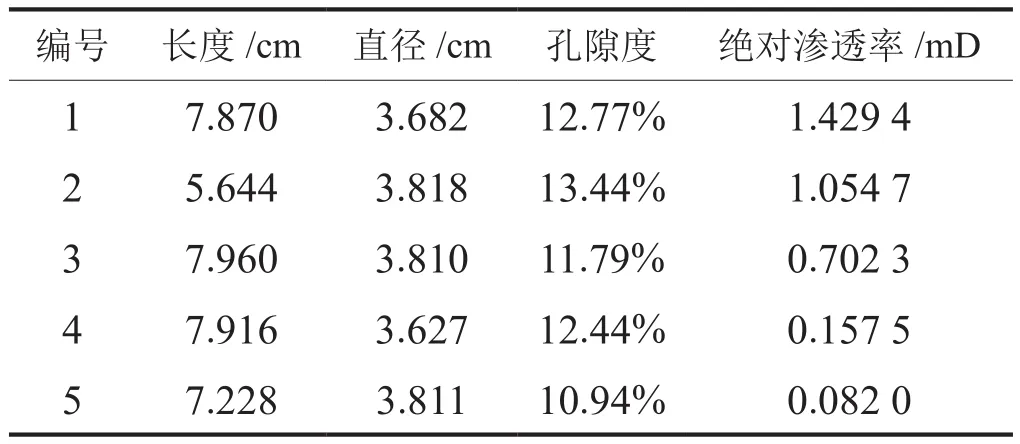
表1 岩样基础数据表
1.2 实验方法
改进的气水两相渗流模拟实验的具体方法如下。
1)选择合适的岩样,放于烘箱内烘干24 h后取出称干重。
2)将岩样放入真空泵中抽真空24 h后注入地层水并加压饱和24 h,同时准备一个10 000 mL中间容器向内充入10 MPa氮气。
3)将其中一块岩样放入岩样夹持器,连接实验流程,加围压至30 MPa。
4)打开ISCO泵和进水阀门2,小流量地向整个实验系统充入地层水,排出实验流程中残留的空气并使进出口压力达到10 MPa,期间保持进出口阀门4、5和进出口联通阀门6为打开状态以保证进出口压力同步变化,达到预期压力后关闭ISCO泵。
5)纯水驱过程:关闭联通阀6,确定进出口压力稳定后再次打开ISCO泵,定流量驱替地层水通过岩样,直到进出口压差不变后关闭ISCO泵和阀门2、7。
6)气驱水过程:打开阀门1、6、7,让进出口压力恢复到同一水平后关闭阀门6。打开流量控制计,设定流量为0。打开增压泵,让流量控制计入口端压力增长到高于环境压力5 MPa并在后续实验过程中一直保持这个压力。为流量控制计设定合适流量开始驱替,待进出口压力稳定后设定流量为0,关闭阀门1,停止进气。
7)水驱气过程:打开阀门2、6,进出口压力恢复到同一水平后关闭阀门6。打开阀门3和ISCO泵,设定合适流量(与气驱水时同一质量流量)驱替地层水进入岩样直至进出口压力稳定后结束实验。
8)更换岩样,重复实验步骤3)~7)。
9)改变围压和环境孔压,重复实验步骤1)~8)。
在所有实验结束后对实验过程中的各种死体积进行测量校正,包括有中间容器体积、夹持器两端体积、ISCO泵体积、管线体积以及各个阀门体积等,尽量减少实验误差。
2 结果与讨论
2.1 理论基础
类比欧姆定律,定义渗流阻力系数为任一点处的压力梯度与该处的流体流速的比值,即单位流速下的压力梯度,即

式中γ表示渗流阻力系数,MPa·min/cm2;p表示气体压力,MPa;v表示流体的流速,cm/min。
在岩样实验中可以表示为:

式中L表示岩样长度,cm;A表示岩样截面积,cm2;Q表示任意压力下的气体流量,mL/min;
当流体为气体时,需要考虑气体压缩性对于流动过程以及计算的影响。真实气体状态方程中,假定温度是常数,同一摩尔质量的气体在不同压力下有如下的状态关系式:

式中V表示该压力下气体的体积,mL;Z表示该压力条件下的压缩因子;psc表示大气压力,一般取0.1 MPa;Vsc表示大气压力下气体的体积,mL;Zsc表示大气压力下的压缩因子,一般取1。
利用式(4)修正岩样中的气体流量:

式中Qsc表示大气压力下的气体流量,mL/min。
因此渗流阻力系数可以被修正为:
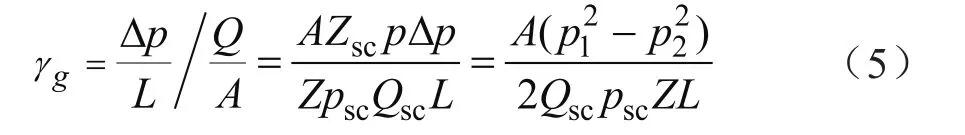
式中γg表示修正后的渗流阻力系数,MPa·min/cm2;p1、p2表示分别为入口和出口断面上的绝对压力,MPa。
改变式(5)的形式,可得到以渗流阻力系数表征的产能模型:
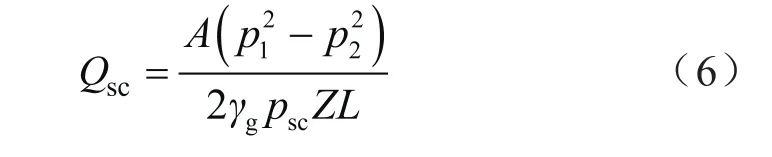
根据苏里格致密砂岩气藏气井控制范围储层已知渗流阻力系数,可以用式(6)计算气井衰竭生产过程中的井底压力与产能变化曲线。根据苏里格致密砂岩气田直井压裂开发特征(图2),设定泄流长度L=100 m,半缝长Y=150 m,厚度h=10 m,p1=30 MPa,计算不同渗流阻力系数下,日产气量与井底压力之间的变化关系图版(图3)。发现在给定渗流阻力系数的情况下,日产气量随井底压力降低而降低,曲线呈“上凸”形态;而随着渗流阻力系数的增大,同一井底压力条件下的日产气量降低显著。表明渗流阻力系数可以有效反映气井的产能,评价致密砂岩气藏的生产能力与开发效果。
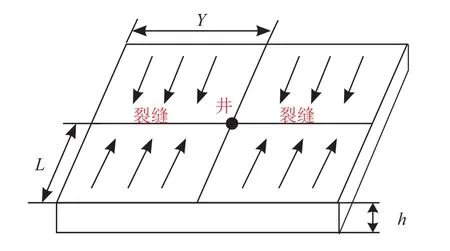
图2 模拟气藏等效线性流示意图
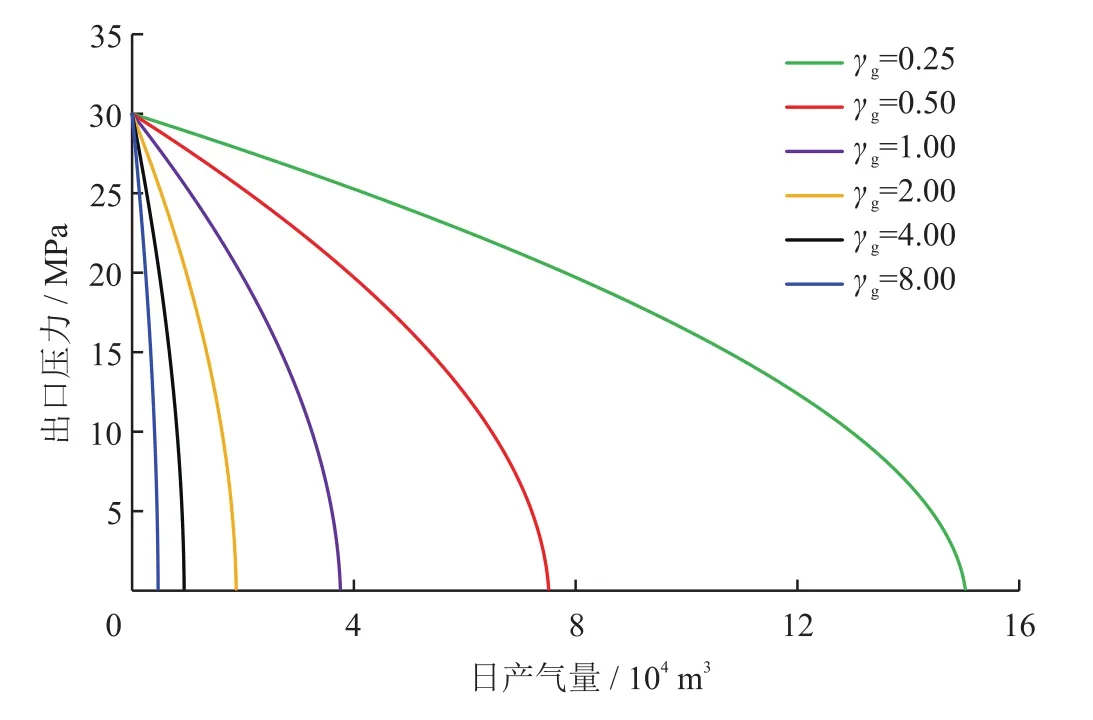
图3 不同渗流阻力系数下日产气量与出口压力关系曲线图
2.2 孔隙压力对渗流阻力系数的影响
在不同孔隙压力的条件下进行水驱气和气驱水实验,实验所用岩样编号为1~5,岩样基础数据如表1所示,对比分析不同孔隙压力下渗流阻力系数的差异。
图4是1号岩样在不同孔隙压力下的渗流阻力系数与进液量PV数、进气量PV数的关系曲线图。可以看出,不论是水驱气还是气驱水过程,同一块岩样在高孔隙压力条件下的渗流阻力系数比常压实验条件下的数值都要大,这说明孔隙压力对于气水两相渗流规律有着一定的影响,但高压条件下与常压下的渗流阻力系数之间的差距气驱水过程相对水驱气过程来说要小得多。
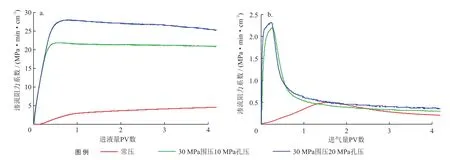
图4 不同孔隙压力下1号岩样的渗流阻力系数与进液/气量PV数关系曲线图
为了表征束缚水或残余气状态下的流动特征,表2列出了进液量PV数、进气量PV数达到稳定状态(4倍PV)时各岩样不同孔隙压力下的渗流阻力系数。从表2中可以看出,不论岩样的渗透率多大,随着孔隙压力的增大,气驱水以及水驱气过程的渗流阻力系数越来越大,这说明不论是气驱水还是水驱气,气水两相渗流的阻力与孔隙压力都是呈正相关关系。
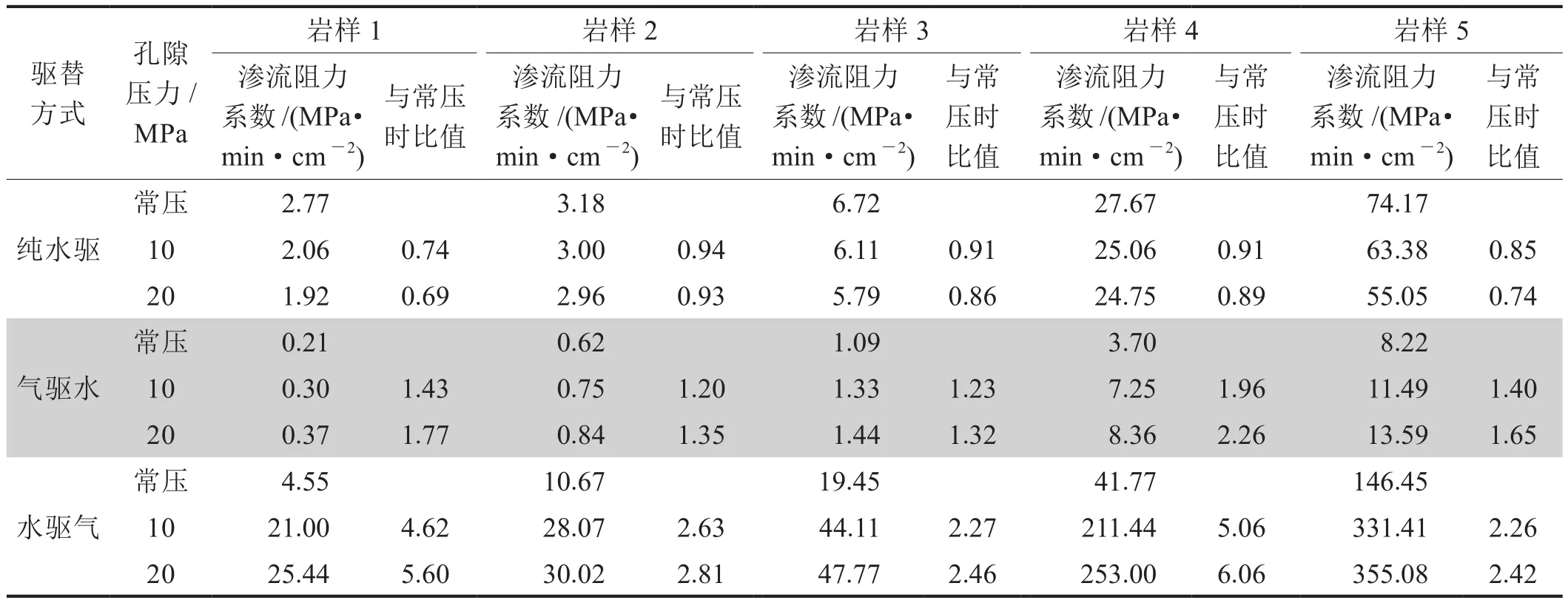
表2 各岩样不同孔隙压力下的渗流阻力系数表
由表2计算可知,纯水驱时10 MPa和20 MPa下的渗流阻力系数与常压下的平均比值分别为0.87、0.82,这表明增大孔隙压力会导致单相流阻力降低,渗流能力提高。气驱水时10 MPa和20 MPa时与常压渗流阻力系数的平均比值分别为1.44、1.67,水驱气时10 MPa和20 MPa条件下与常压渗流阻力系数的平均比值分别为3.37、3.87,高压下气水两相渗流流动阻力比之常压条件要大得多,但10 MPa和20 MPa之间的差距并不大,尤其是水驱气过程,趋势更为显著。这说明孔隙压力介于10~20 MPa之间时,当气水两相渗流进入稳态时,渗流阻力并没有发生急剧变化,孔隙压力的继续增大对于渗流阻力的影响变小,气水两相的渗流能力在一定阶段后并不随孔隙压力的增大而发生明显变化。
为了更直观地展现渗流阻力系数与孔隙压力之间的关系,对纯水驱、水驱气以及气驱水3种情形下的渗流阻力系数与孔隙压力的关系进行拟合,结果如表3所示。
从表3中可以看出,纯水驱过程渗流阻力系数与孔隙压力之间的拟合公式中的系数为负数,渗流阻力系数随孔隙压力的增大而逐渐下降,而水驱气和气驱水过程则逐渐升高。3种情形下的渗流阻力系数与孔隙压力都有较好的对数关系(拟合公式相关系数都在0.95以上),因此可以统一表示为以下的形式:
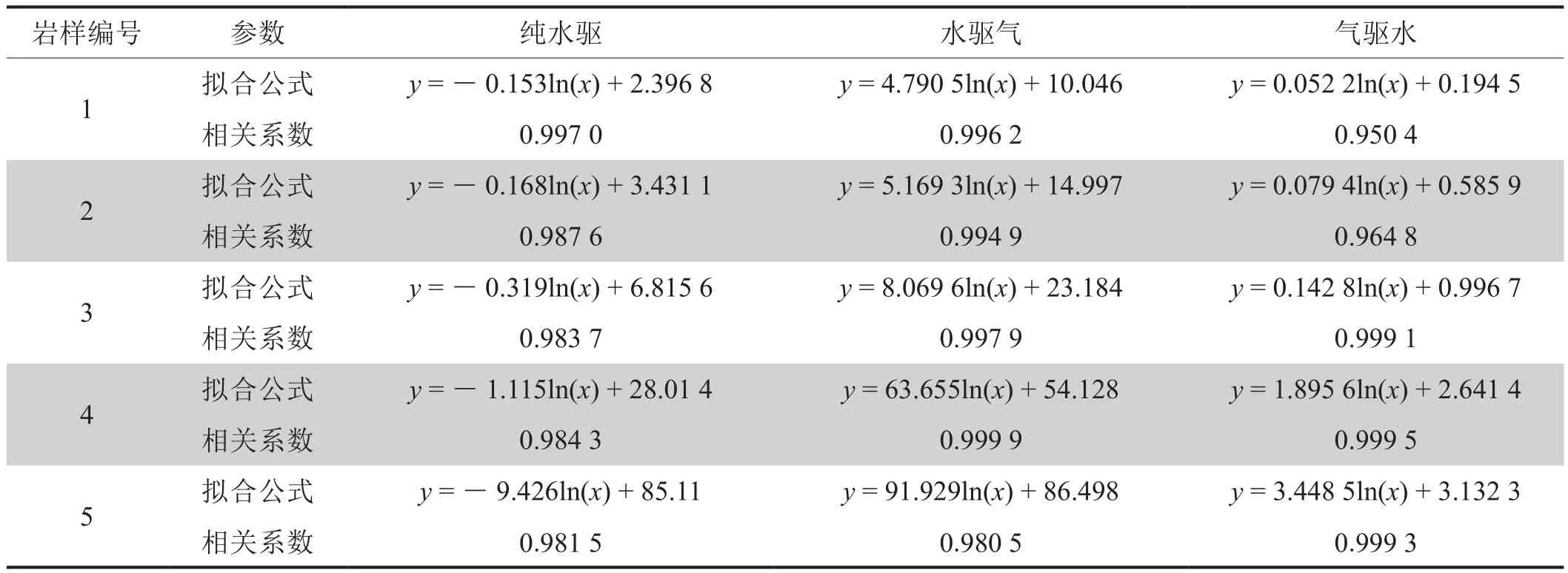
表3 纯水驱、水驱气和气驱水过程渗流阻力系数与孔隙压力拟合公式统计表
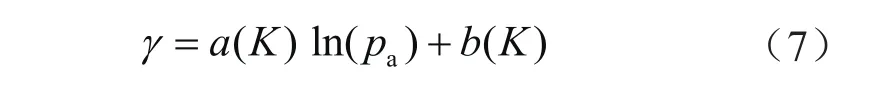
式中K表示绝对渗透率,mD;pa表示孔隙压力,MPa;a、b均为与渗透率相关的系数。
2.3 渗透率对渗流阻力系数的影响
以常压和20 MPa孔隙压力实验条件为例,比较分析5块岩样的渗流阻力系数的差异及规律。图5是纯水驱、水驱气和气驱水过程中不同岩样的渗流阻力系数随进液量PV数、进气量PV数的变化曲线图。可以看出,不论是纯水驱、水驱气还是气驱水过程,随着岩样渗透率的降低,渗流阻力系数都会逐渐增大。
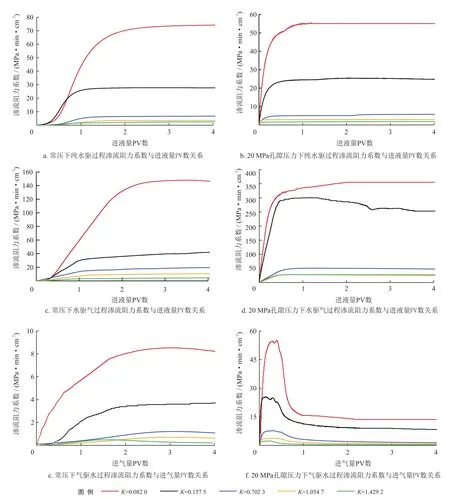
图5 不同岩样纯水驱、水驱气、气驱水过程渗流阻力系数与进液量PV数、进气量PV数关系曲线图
图6是纯水驱、水驱气和气驱水过程中不同岩样的渗流阻力系数随渗透率的变化曲线图。从图中可以看出,不论是纯水驱、水驱气还是气驱水过程,渗流阻力系数与渗透率都有着较好的负指数关系,且指数值都接近-1。
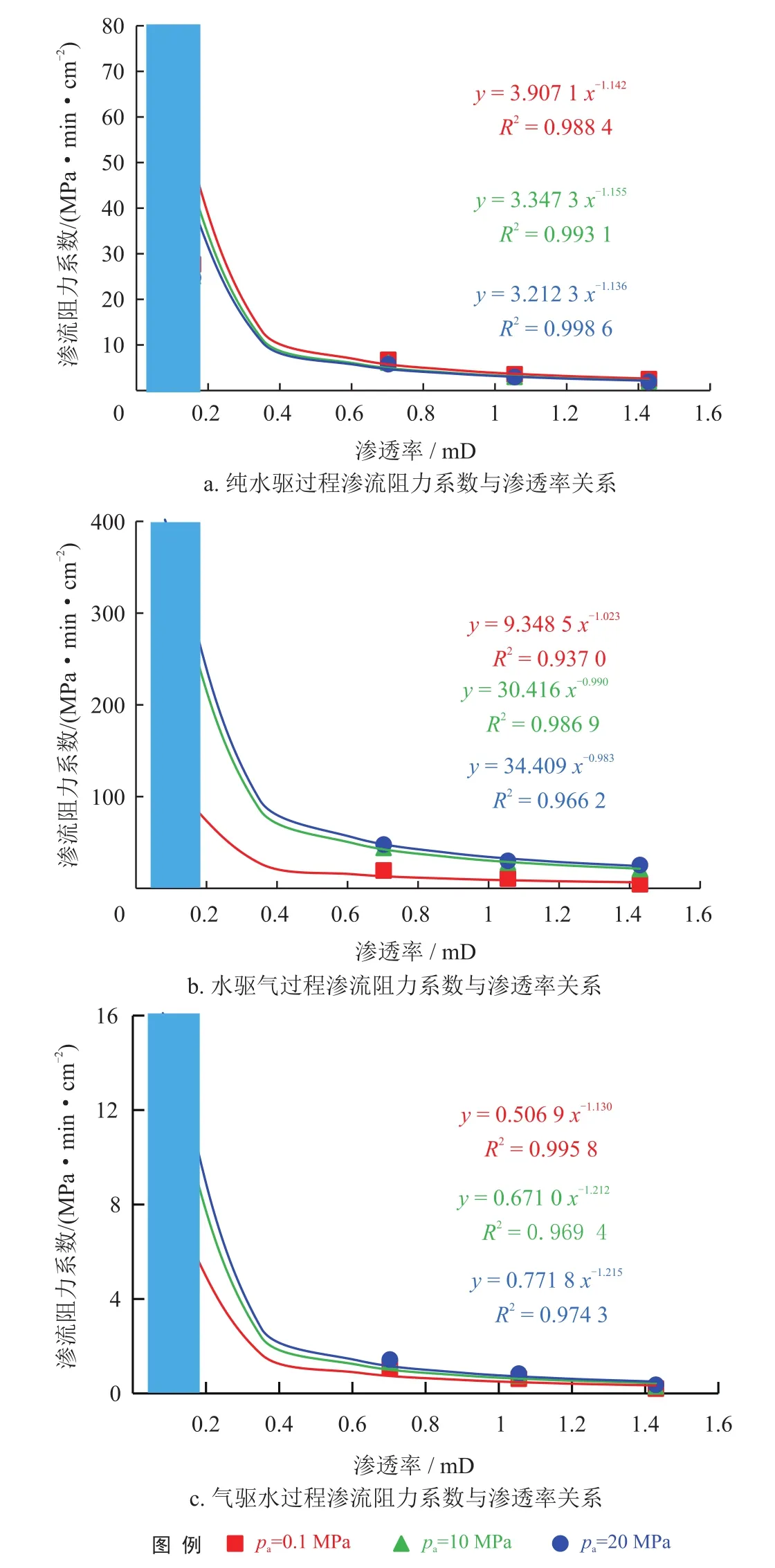
图6 不同孔隙压力下渗流阻力系数与渗透率关系曲线图
这说明渗流阻力系数与渗透率成反比关系,可表示为:

式中c表示与孔隙压力相关的系数。
另外,从图6中还可以看到,渗透率降低至一定程度(图中涂蓝区域)时渗流阻力系数与较高渗透率时会有一个比较大的差距,尤其在渗透率低于0.1 mD时,这种差异会变得更加明显。一般地,称K=0.1 mD为储层致密临界渗透率,这也是界定致密砂岩气藏的标准[19-20]。说明致密砂岩气藏孔隙压力对于渗流阻力系数影响更大。
2.4 渗流阻力系数数学模型的建立
分别从系数拟合和减少参数两个角度出发分析实验数据,建立渗流阻力系数数学模型。
2.4.1 模型一(系数拟合法)
表3分别给出了纯水驱、水驱气和气驱水过程渗流阻力系数与孔隙压力之间的对数拟合关系式,结合式(7)列出3种情形下不同渗透率对应的系数a、b(表 4)。
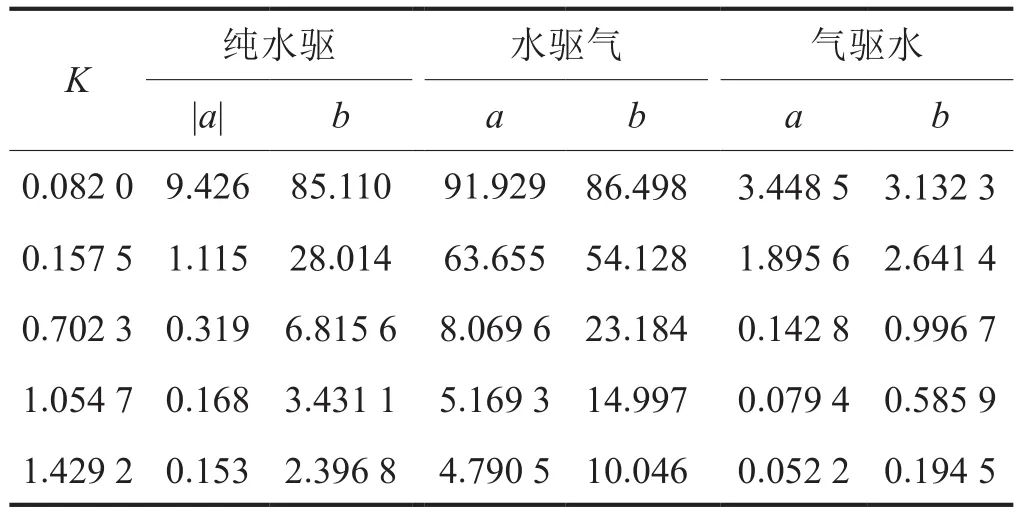
表4 不同岩样渗透率对应的系数a、b表
对气驱水过程的系数a、b与渗透率的关系进行曲线拟合,结果如图7所示。
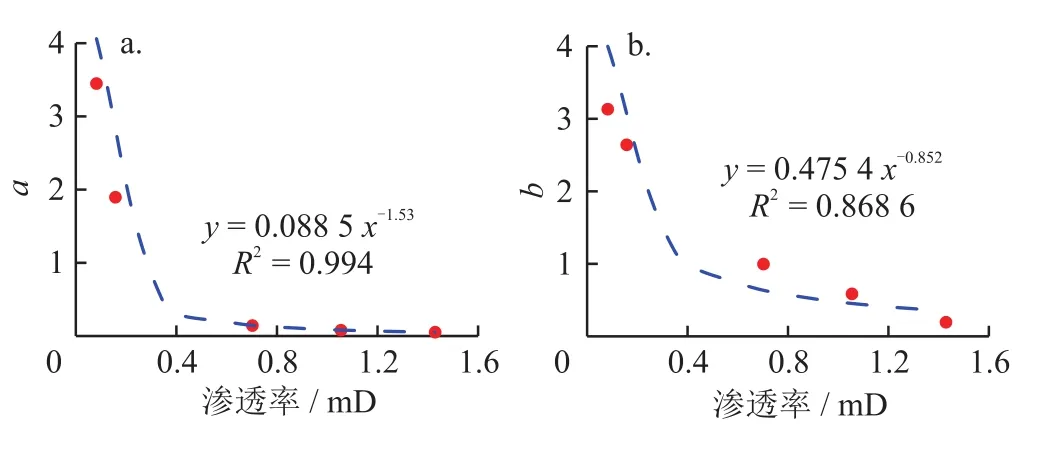
图7 气驱水过程系数a、b与渗透率关系曲线图
将系数a、b用渗透率K表达,并将其代入公式(7),可得:
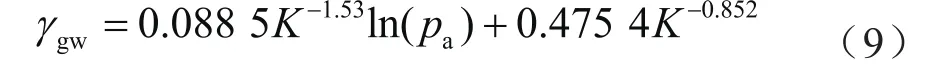
式中γgw表示气驱水渗流阻力系数,MPa·min/cm2。同样的方法处理纯水驱以及水驱气过程的系数a、b,可得:
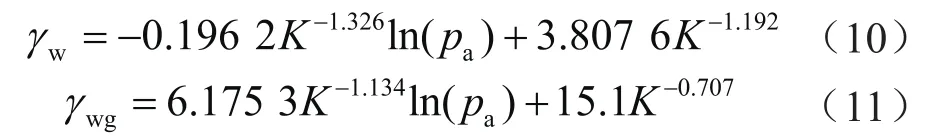
式中γw表示纯水驱渗流阻力系数,MPa·min/cm2;γwg表示水驱气渗流阻力系数,MPa·min/cm2。
式(9)~(11)即利用系数拟合方法得到的渗流阻力系数数学模型(模型一)。
2.4.2 模型二(减少参数法)
从图6的拟合曲线可以看出,渗流阻力系数与渗透率保持了一个较好的反比关系,如同式(8)所示。为了消除渗透率对于渗流阻力系数的影响(减少“渗透率”这个参数),定义广义渗流阻力系数为渗流阻力系数与渗透率的乘积,即

式中ζ表示广义渗流阻力系数,MPa·min·mD/cm2。
绘制气驱水时广义渗流阻力系数与孔隙压力的关系曲线并拟合,结果如图8所示。
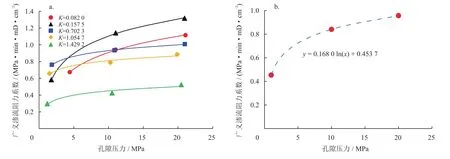
图8 不同岩样气驱水过程广义渗流阻力系数与孔隙压力关系及标准化曲线图
利用数值平均的方法,分别取孔隙压力为1 MPa、10 MPa、20 MPa,将其分别代入图8-a中的5个不同岩样的拟合曲线(表5),得到气驱水过程广义渗流阻力系数的取值,再将不同岩样下的数值平均化处理得到气驱水过程广义渗流阻力系数与孔隙压力的关系。对广义渗流阻力系数平均值与孔隙压力进行曲线拟合,结果如图8-b所示。
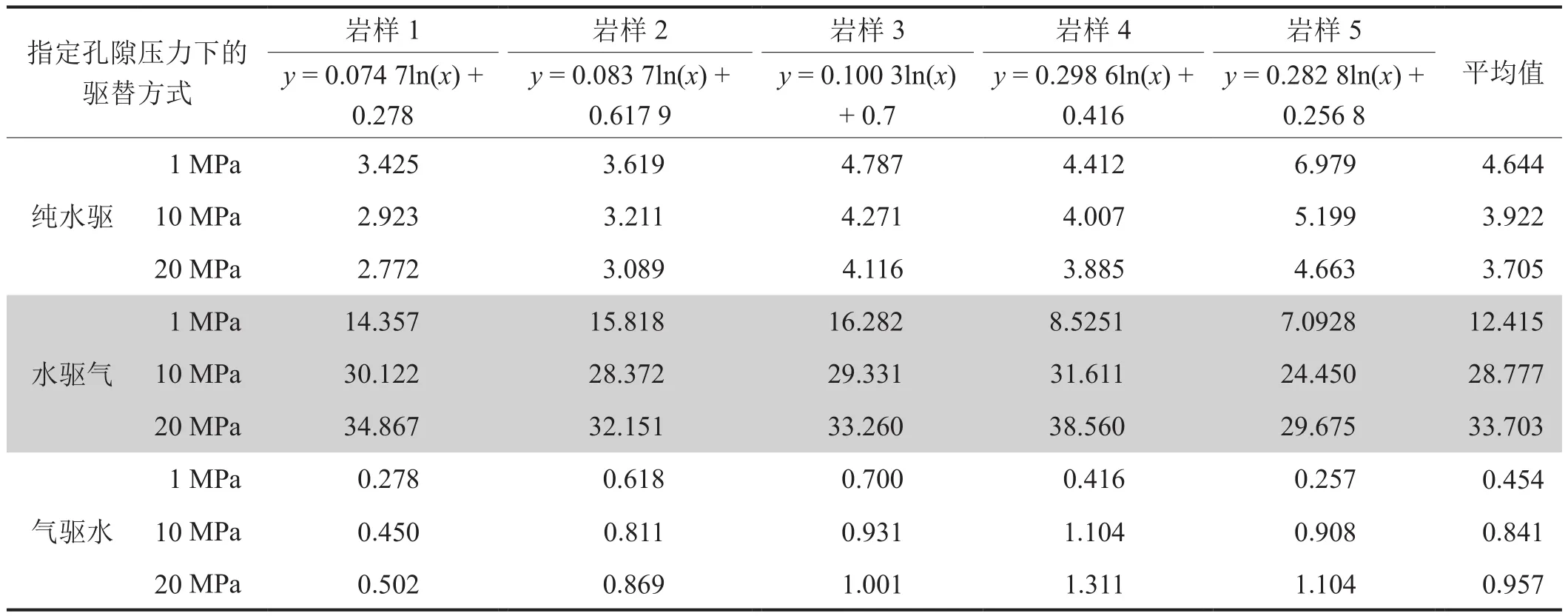
表5 不同岩样纯水驱、水驱气、气驱水过程指定孔隙压力下的广义渗流阻力系数表 单位:MPa·min·mD/cm2
气驱水过程广义渗流阻力系数与孔隙压力的关系表达式为
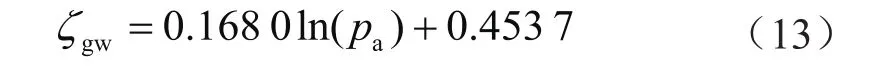
式中ζgw表示气驱水广义渗流阻力系数,MPa·min·mD/cm2。
将式(13)代入式(12)可得气驱水渗流阻力系数为
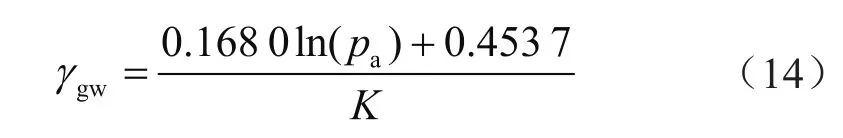
同样的方法可以得到纯水驱以及水驱气过程各岩样指定孔隙压力下的广义渗流阻力系数(表4)及其与孔隙压力的关系,进而得到纯水驱和水驱气过程的渗流阻力系数,分别为:
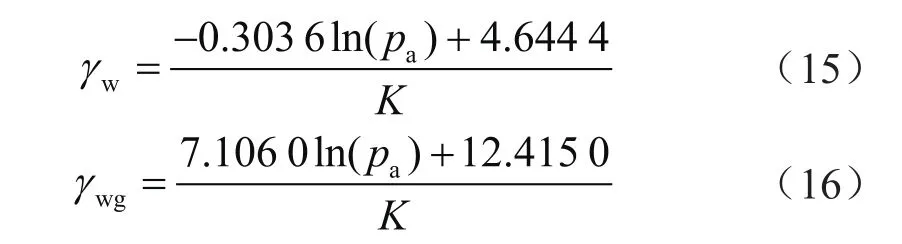
式(14)~(16)即利用减少参数方法得到的渗流阻力系数数学模型(模型二)。
2.5 渗流阻力系数数学模型的验证与应用
2.5.1 模型的验证
在如图9所示的岩样衰竭开发实验中,地层条件下的气体体积流量可由式(2)推导得到。
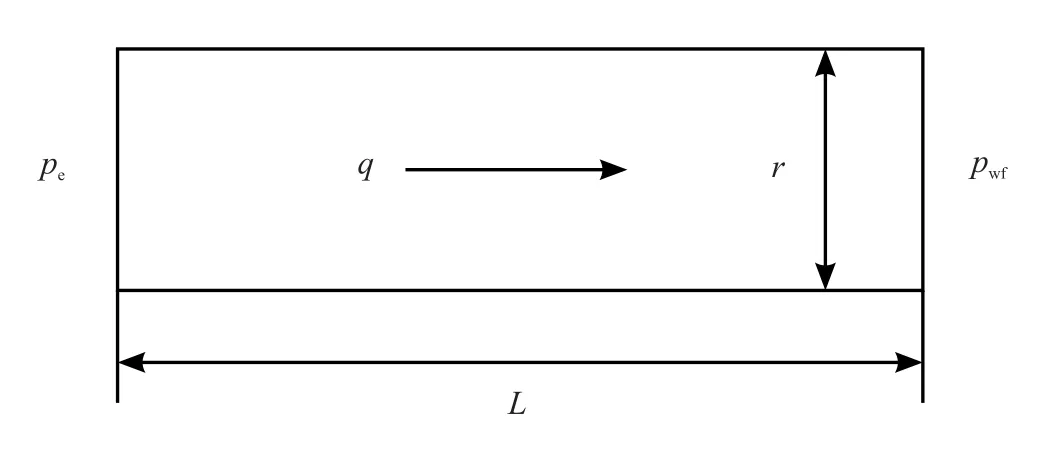
图9 岩样衰竭开发实验示意图

式中q表示地层条件下的气体体积流量,mL/min。
地面条件下的气体体积流量为
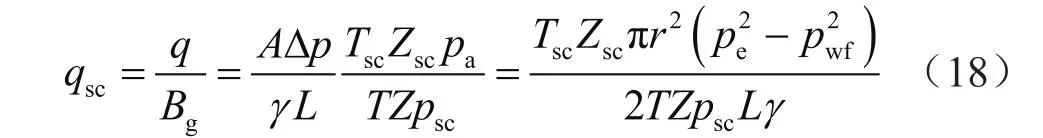
式中qsc表示地面条件下的气体体积流量,mL/min;Bg表示体积系数;Tsc表示标准状态温度,K;T表示实验环境温度,K。
Z、γ都是pa的函数,整理方程得
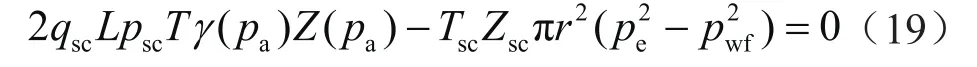
式中pa= (pe+ pwf)/2,γ(pa)的形式由渗流阻力系数数学模型确定。
基于式(19),利用Matlab编写程序完成数值模拟,程序实现的思路如下。
1)赋值初始条件:pe(0)=30 MPa、pwf(0)=30 MPa;
2)衰竭开发起始点:定产开发,qsc是定值,2qscLpscT、TscZscπr2都是常数。假定起始点(第1点)pe不变即pe(1)=30 MPa,pwf(1)由方程(19)计算得到
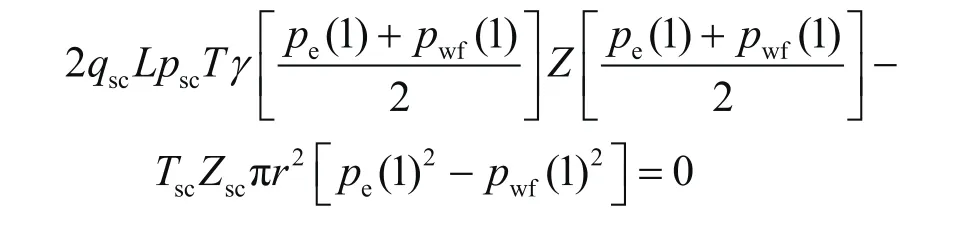
3) 第 2点 :将 ωpe(1) + (1-ω)pwf(1)(ω 为比例系数)赋值给pe(2),pwf(2)由方程(19)计算得到;
4)后面依次循环直到达到终止条件(pwf达到废弃压力,设定为3 MPa):
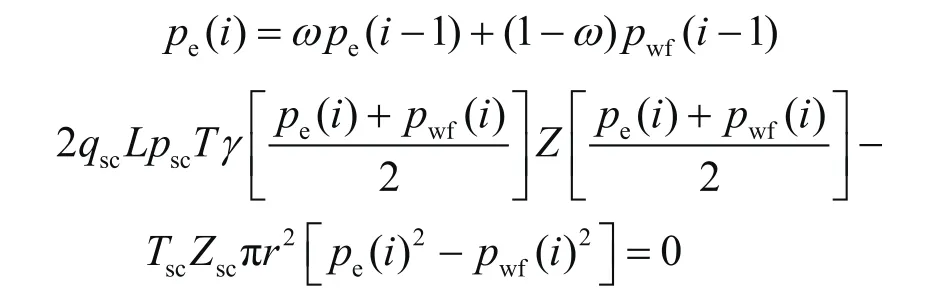
最终得到pe、pwf随时间的变化曲线,与实验数据相对比来验证渗流阻力系数模型的准确性和适用性,结果如图10所示。
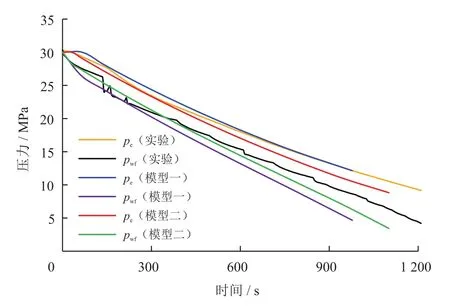
图10 渗流阻力系数模型数值模拟结果与实验数据对比图
从图10可以看出,渗流阻力系数模型一与模型二的数值模拟结果与实验数据都基本符合,这说明不论是模型一还是模型二,都是正确有效的。
2.5.2 基于渗流阻力系数模型的产能方程
确定渗流阻力系数模型的准确性和适用性之后,将两个模型运用到圆形等厚均质致密定压边界地层模型(图11)中,建立产能方程。
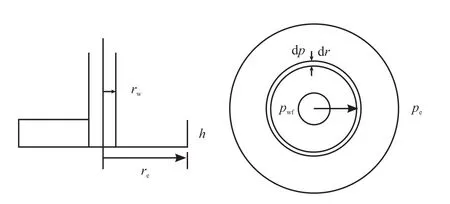
图11 圆形等厚均质定压边界地层模型图
以模型一为例,在该地层模型中,渗流阻力系数表达为
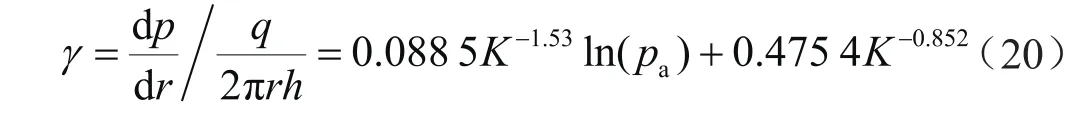
径向距离r处圆形渗流截面上的气体体积流量(地层条件)为
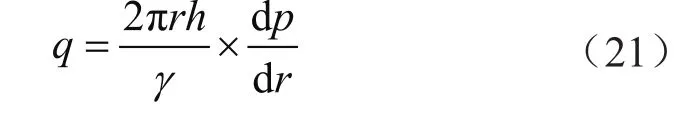
地面条件下的对应气体体积流量为
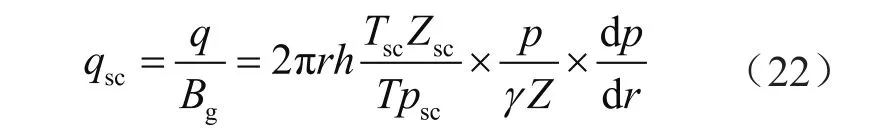
整理上式可得
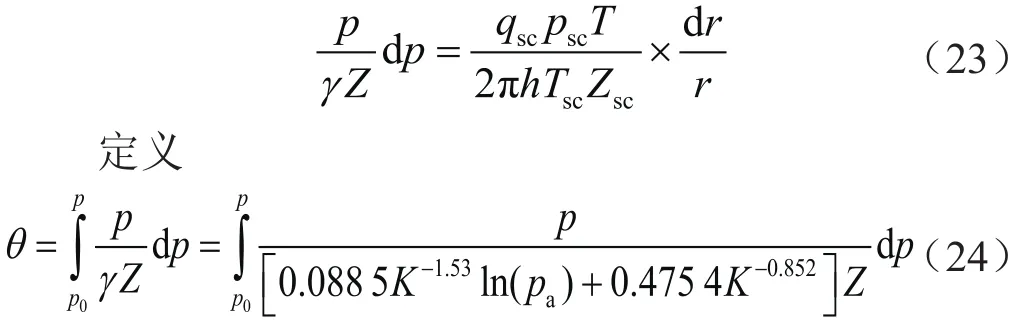
将式(24)代入式(23)并沿径向距离积分,得
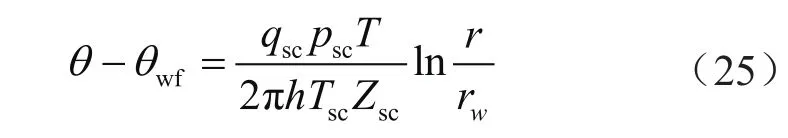
若考虑地层伤害,式(25)则写成
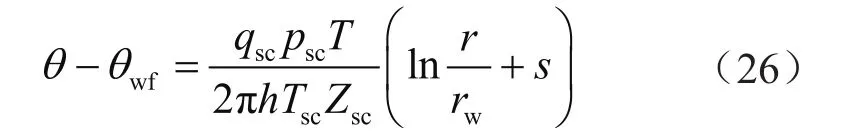
式中s表示表皮因子。
在气层外边界处有:
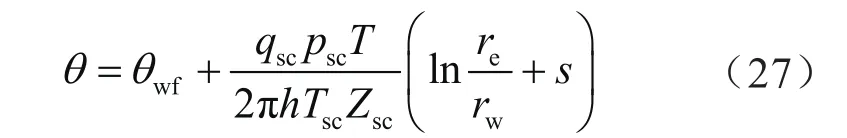
由式(27)可以得出气井稳产条件下的产量计算公式,即
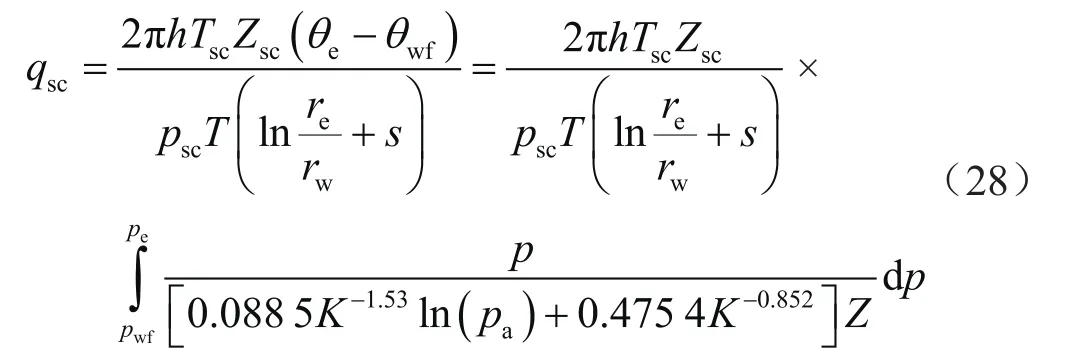
式(28)即基于渗流阻力系数模型一的产能方程。同理可得基于渗流阻力系数模型二的产能方程为:
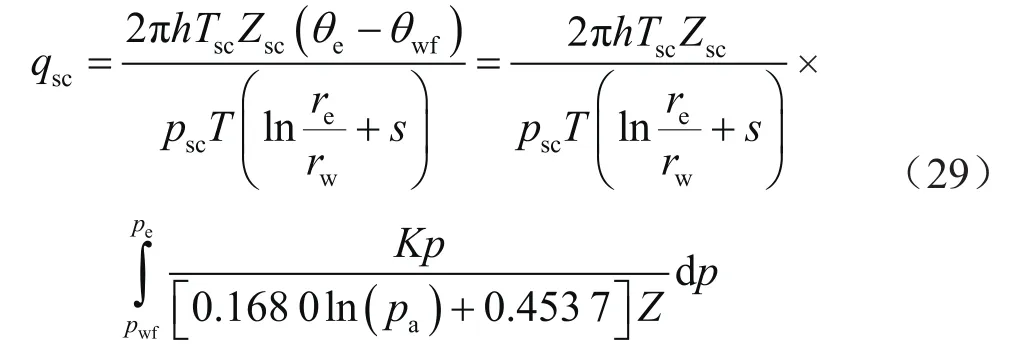
2.5.3 实例分析
以苏里格气田实际气井为例(表6),计算气井的IPR曲线。通过Matlab数值模拟的方法分别计算两个产能方程式(28)~(29)中流量与井底流压之间的关系,建立气井生产的IPR曲线。并与传统产能方程的IPR曲线进行对比(图12),可以看出,渗流阻力系数模型推导的产能方程与传统产能方程[21]计算的IPR曲线基本一致,与传统模型无阻流量之间的误差都不足10%,符合气藏工程要求,说明两个渗流阻力系数模型得到的产能方程都是可信的。

表6 气井基础数据表
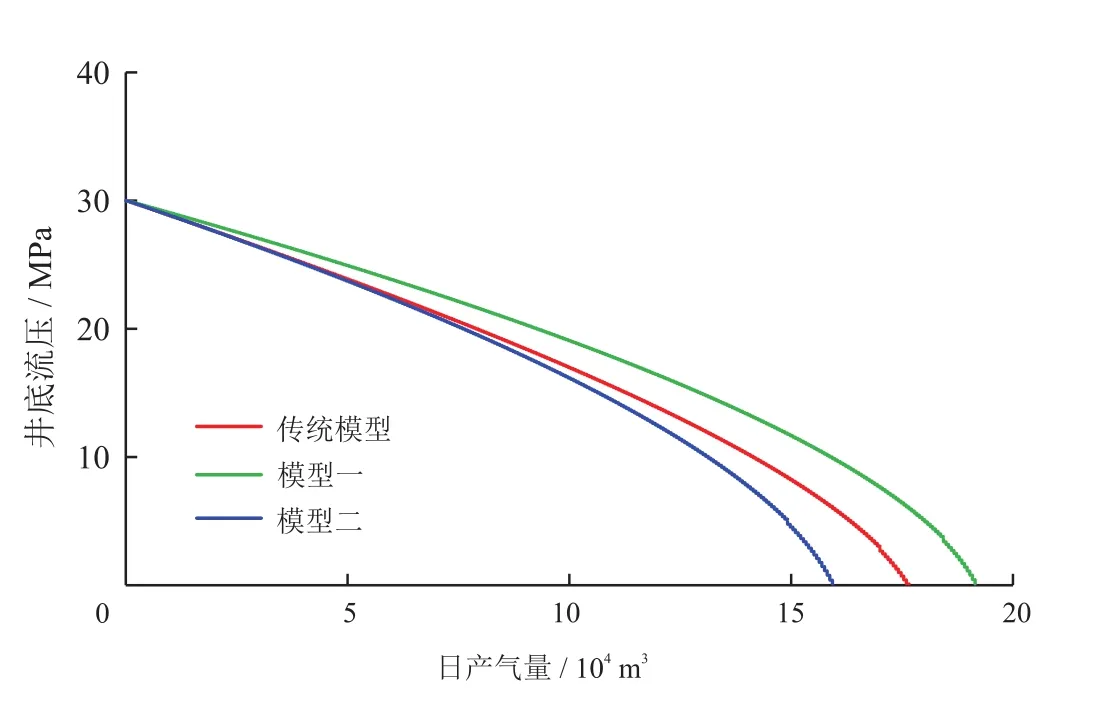
图12 三种产能模型计算的IPR曲线对比图
3 结论
1)定义了表征气水两相在致密砂岩气藏储层多孔介质中流动阻力的渗流阻力系数,该系数消除了实验岩样几何尺寸与驱替速度的影响,具有普适性。在气驱水实验的基础上,借助渗流阻力系数,推导了致密砂岩气藏新的产能计算模型。
2)不论是水驱气还是气驱水过程,同一块岩样在高孔隙压力条件下的渗流阻力系数比常压实验条件下的数值都要大,这说明高孔隙压力对于气水两相渗流有着一定的影响。但孔隙压力的持续增大对于气水两相渗流阻力的影响变小,气水两相的渗流能力在一定阶段后并不随孔隙压力的增大而发生明显变化。不论是纯水驱、水驱气还是气驱水过程,渗流阻力系数与孔隙压力之间都有着较好的对数关系。
3)不论是纯水驱、水驱气还是气驱水过程,随着岩样渗透率的降低,渗流阻力系数都会逐渐增大,两者有着较好的负指数关系,且指数值都接近-1。这说明渗流阻力系数与渗透率成反比。
4)基于实验数据,从系数拟合和减少参数两个角度出发建立了两个渗流阻力系数数学模型,通过Matlab数值模拟的方法验证了两个数学模型的正确性与适用性,并在两个模型的基础上推导了全新的产能方程,气井实例计算的IPR曲线与传统产能方程基本一致。

