一种基于扩张残差网络的雷达信号识别方法

陈 琳， 唐 骏， 余 跃， 张旭洋

(厦门理工学院，福建 厦门 361000)

0 引言

随着雷达技术的发展，新体制雷达开始取代传统的常规脉冲雷达，使雷达所处电磁环境愈加复杂，同时也提高了雷达信号识别难度[1]。基于传统五参数脉冲描述字的雷达信号识别方法无法满足新的军事可靠性要求。脉内分析方法可以获取图像脉内特征信息[2]。文献[3]提出了基于脉内瞬时频率特征的雷达信号调制识别方法，在信噪比为-5～5 dB的条件下，实现对4种不同调制类型信号的识别；文献[4]采用Choi-Williams时频分布，提出了改进的半监督朴素贝叶斯学习算法。

然而，在实际环境中，雷达信号容易受到噪声干扰，从而导致脉内特征丢失，以致识别准确率下降[5]。

近年来，深度学习技术在信号、图像识别等领域取得了优异成果。因此，国内外众多学者将深度学习运用于雷达信号识别领域。文献[6]提出了一种基于集成深度学习模型的信号分选方法，通过堆叠不同类型深度信念网络，进一步提高信号识别率，但此类方法网络结构复杂，导致训练耗时长；文献[7]提出了基于雷达信号脉内特征和卷积神经网络的识别方法，引入新的Cohen类时频分析核函数，可以提高低信噪比条件下雷达信号的识别率；文献[8]利用卷积核与匹配滤波器具有相似性的特性，提出了一种基于卷积神经网络的雷达信号检测方法，但此方法只对4种信号进行了识别。

本文提出一种基于扩张残差网络的识别方法，对扩张残差网络(Dilated Residual Network，DRN)[9-10]进行改进，同时，在网络结构中加入特征融合提取模块(Distinguishing Feature Fusion Extraction module，DFFE)[11]，利用几种Cohen类分布结果融合得到的时频图像，识别不同信噪比条件下的雷达调制信号，并进行仿真分析。其中，调制信号类型包括有单载频、频率编码(FSK)、相位编码(BPSK,Frank,P1～P4)，以及LFM，NLFM这10类信号[12]。

1 雷达信号预处理

1.1 时频分析

雷达信号是非平稳信号，而时频分析作为非平稳信号处理的重要工具能够有效分析雷达信号的特征，并能充分描绘信号时频联合特性[13]。Wigner-Ville 分布(WVD)是一种具有良好时频分辨率及聚集性的时频分析方法，然而该方法易受到交叉项干扰。为了克服WVD的缺点，常用做法是引入不同的核函数对来抑制信号交叉项，这种改进的时频分析方法就称为Cohen类时频分布，其一般形式为[14]

(1)

(2)

式中:t和f分别为时间和频率；τ和ν分别为时延和频偏；φ(τ,ν)为核函数;Az(τ,ν)为模糊函数;z(t)为时域信号；z*(t)为共轭信号。常见的Cohen类时频分布有伪Wigner-Ville分布(PWVD)、平滑伪Wigner-Ville分布(SPWVD)和Choi-Williams分布(CWD)等，其定义分别为[15]

(3)

(4)

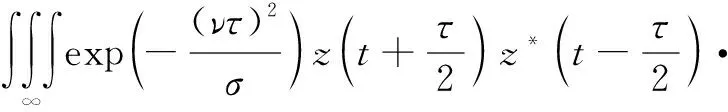
(5)

式中:h(τ)为频域方向窗函数;g(u-τ)为时间方向窗函数;exp(-ν2τ2/σ)为CWD的核函数,能有效控制整体平滑性，且σ取值为1，既能有效控制交叉项干扰，又具有较好的时频分辨率。

在本文中，将上述时频分析所得结果分别定义为YPWVD,YCWD,YSPWVD，利用加权平均融合算法对上述3种时频图像进行融合。加权平均融合的一般形式定义为

(6)

式中:Y为融合后图像；Wj为加权因子；Yj为原始图像。因为CWD变换受交叉项干扰最小，而PWVD变换及SPWVD变换对交叉项干扰有一定抑制作用，3种变换中包含的特征并不完全相同，将三者进行融合，可以得到更丰富的信号特征，有利于后续识别。融合算式为

Ys=0.5YCWD+0.25YPWVD+0.25YSPWVD

(7)

式中，Ys为融合后的时频图像。

1.2 时频图像预处理

由于将时频图像直接输入到深度学习网络容易导致网络运行速度慢，因此需要对其进行处理以减小输入网络的数据量，处理步骤如下：

1) 对时频图像进行灰度化处理，既能减少数据量，又能有效保留时频分布特征；

2) 对灰度图进行开运算，能够去除时频图像中产生的大量类型的底噪，有利于后续识别；

3) 调整图像尺寸，将图像大小从800像素×800像素重置为224像素×224像素，该方法既能有效缩小图像尺寸，又能保留更好的图像细节质量。

图1(a)为融合后时频图像预处理流程图,图1(b)表示SNR为-4 dB时P3码信号的时频图像预处理。

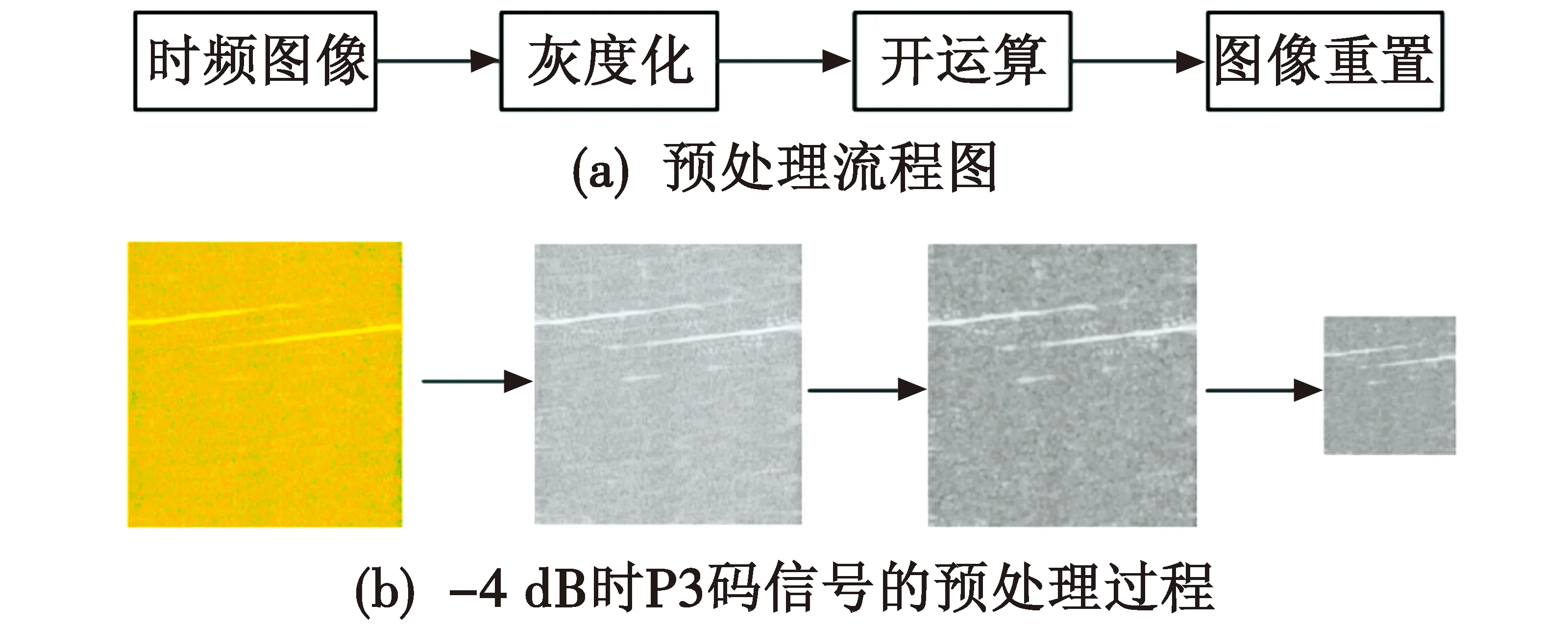
图1 图像预处理Fig.1 Image preprocessing

由图1可知，时频图像通过一系列的处理后，减小了数据量，同时也较完整地保留了图像特征，适合输入深度学习网络。

2 基于DFFE和扩展残差网络的信号识别

2.1残差网络

为了简化深层网络训练，HE等[16]提出一种由残差块堆叠成的新网络框架——残差网络(Residual Network,ResNet)，其中，残差块可表示为

xl+1=h(xl)+F(xl,Wl)

(8)

式中:xl为l+1层的输入；h(xl)为映射部分;F(xl,Wl)为残差部分。

图2所示为残差块基本结构。其中，x为该残差块的输入，经过2层卷积后加上跳跃连接构成残差块的基本结构。

图2 残差块基本结构Fig.2 Structure of residual block

2.2 扩张卷积

神经网络中卷积层后一般会添加池化层，其目的是对特征图进行下采样操作[17]，该操作具有压缩和聚合特征的优点，同时能够减小特征图尺寸，使后续卷积层的感受野增大，扩大得到特征信息的范围，然而在下采样处理中会损失部分信息。针对此问题，本文在构造网络时仅采用一个池化层以减小特征图尺寸，并引入扩张卷积，在增大感受野的同时尽可能保留信号特征。扩张卷积定义为[18]

(9)

式中:F为二维图像；s表示其定义域；k为核函数；t表示其定义域；*l表示扩张倍数,又可以称l为扩张因子;p=s+lt，表示扩张卷积的定义域。

在卷积层中扩张因子l是关键参数，当l≠1时，感受野大小为

Fi+1=Fi*2ikii=0,1,2,…,n

(10)

式中:Fi+1为计算得到的下一层感受野；ki为卷积核尺寸大小。

图3所示为感受野大小的扩张过程,图3(a)～3(c)所对应的扩张因子分别为1,2,4的感受野，与普通卷积相比，使用不同扩张因子的扩张卷积能够使感受野呈指数扩张，保证卷积核参数不变，在卷积过程中保证特征信息不丢失，从而获得更好的特征图。

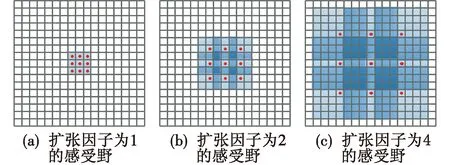
图3 感受野的指数扩张Fig.3 Exponential expansion of receptive field

2.3 特征融合提取模块DFFE

由于不同雷达信号的相似区域较大，特征区域较小，因此LI等[11]提出了特征融合提取模块来解决该问题。该模块中能够突出相关性高的空间区域，同时对几种不同卷积核的运算进行融合，提高了特征图的分辨率。因此，本文在网络结构中加入DFFE模块，能够强调有效特征区域，使获得的特征信息更加完整，有利于最后得到具有高分辨率的特征图。

2.4 DRN模型结构

本文提出的DRN模型[9]是结合DRN-C模型[10]构建的新DRN模型。本文设计的DRN+DFFE模型结构如图4所示，图中，虚线部分表示该单元需要采用尺寸为1×1的卷积核来调整特征输入图的维度大小，解决特征维度不匹配的问题。其中，Conv_1采用7×7的卷积核，Conv_2～Conv_5均使用残差块，并在Conv_3输入前加入DFFE模块，有利于提取出信号时频图中的有效特征区域，减少无效区域的干扰，且将Conv_4，Conv_5中的普通卷积分别采用扩张因子为2，4的扩张卷积替代，该操作有利于增大卷积的感受野，减少空间层次信息丢失的情况出现。由于扩张卷积通过加入空洞增大感受野会导致网格伪影现象，因此本文在Conv_5的末尾加入了扩张因子分别为2，1的扩张卷积组Conv_6，Conv_7，能够有效防止出现伪影。本文在每个ReLU函数激活前均加入批标准化层，可以有效避免反向传播时神经网络底层梯度消失[8]。

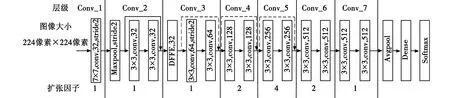
图4 DFFE+DRN网络结构Fig.4 DFFE+DRN network architecture

3 仿真结果与分析

3.1 实验参数设置

雷达信号模型定义为[12]

z(t)=Aexp[j(2πf0t+φ(t)+θ0)]+n(t)

(11)

式中:A为振幅;θ0为初始相位;φ(t)为瞬时相位;n(t)为高斯白噪声。本文主要研究10类雷达信号的识别，其中,信号脉冲宽度设置为WP=2 μs，采样频率设置为fs=400 MHz。

表1所示为雷达信号具体参数。

表1 雷达信号具体参数设置

表1中给出雷达信号的所有具体参数设置范围。信噪比范围设置为-10～10 dB，步长为2 dB，每个信噪比条件下，每种信号类型生成1000个脉冲，然后对信号进行时频分析和预处理，构建数据集。将80%的数据用于训练，20%的数据用于测试。本文所有的网络训练均在Tensorflow2.0.0和keras2.3.1环境下实现。

3.2 不同方法识别性能对比

本文采用DRN+DFFE模型测试CWD变换、PWVD变换和SPWVD变换融合的方法，并与CWD变换和PWVD变换融合、CWD变换和SPWVD变换融合、CWD变换、PWVD变换以及SPWVD变换等方法进行比较，分析其对雷达信号识别结果的影响。本文采用信号识别准确率(Accuracy)评估识别效果。

图5所示为上述不同模型方法对10类雷达信号整体的识别结果。

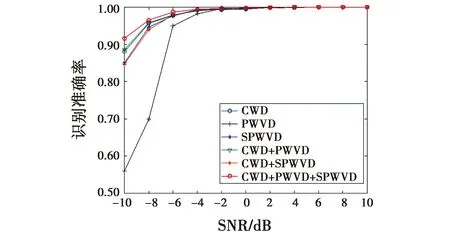
图5 不同时频图像的整体识别结果Fig.5 Overall recognition results of different time-frequency images

在SNR为-10 dB时，本文方法对10类信号的整体识别准确率为91.6%，且在不同的信噪比条件下，该方法的识别准确率均高于其他方法。这是因为：PWVD变换只对频域方向的交叉项进行抑制；SPWVD变换能够对时域及频域方向的交叉项进行抑制，但会造成图像分辨率损失；PWVD变换和SPWVD变换分别与CWD变换融合时，CWD变换受到PWVD变换或SPWVD变换的干扰较大不能突出优势，所以这几类方法对雷达信号识别效果均低于本文方法。本文将CWD变换、PWVD变换和SPWVD变换进行融合，以CWD变换为基础，融合了3种变换的优点，使信号特征得到了互补，同时提高信号时频图中微小的特征，获到高质量的特征图，在低信噪比条件下具有更高的识别准确率以及更好的稳定性。

3.3 不同网络结构识别性能对比

测试DFFE模块对10类信号识别性能的影响，同时将DRN+DFFE与常用的深度学习模型CNN、DRN[9]及DRN-C[10]进行比较，测试DRN+DFFE结构的识别性能。仿真结果如图6和图7所示。

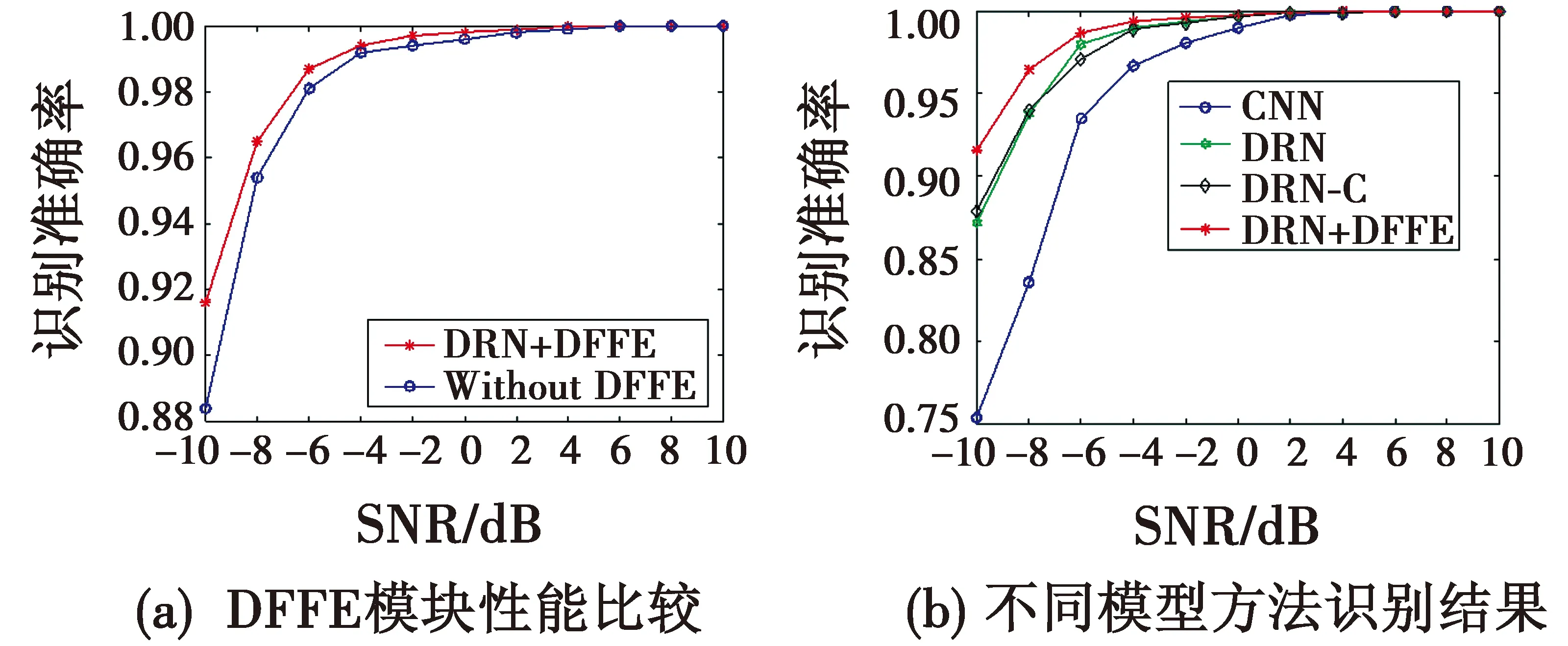
图6 不同模型方法的整体识别结果Fig.6 Overall recognition results of different models

图6(a)表示DFFE模块对10类信号整体的识别准确率影响。结果表明，在不同信噪比条件下，加入DFFE模块均能明显提高对雷达信号的识别率。图6(b)表示不同模型方法对10类信号整体的识别准确率，可以看出，在不同信噪比环境下，本文所提方法性能最优。在SNR为-6 dB时，改进DRN+DFFE的识别准确率达到98.7%，高出DRN约 0.7%，高出DRN-C约 1.6%，高出CNN约5.2%。CNN模型容易丢失部分信息，对部分特征相似性大的信号识别困难；DRN模型中存在网络伪影现象，且DRN和DRN-C模型中未引入DFFE模块，网络中特征提取效果不如本文所提模型。

图7所示为不同模型方法对10类信号的识别结果。

图7 不同模型方法的10类信号识别结果Fig.7 Recognition results of different methods for 10 types of signals

由图7可以看出，本文所提DRN+DFFE模型对10类信号识别结果更优。由图7(f)～7(j)可知，在低信噪比下,Frank码、P1码、P3码、P4码等信号的识别效果较差。

为了进一步比较DRN+DFFE，DRN，DRN-C以及CNN模型对时频特征相似信号的识别性能，图8所示为当信噪比为-10 dB时，4种模型识别LFM、Frank码、P1码、P3码、P4码等信号的混淆矩阵(Confusion Matrix)。

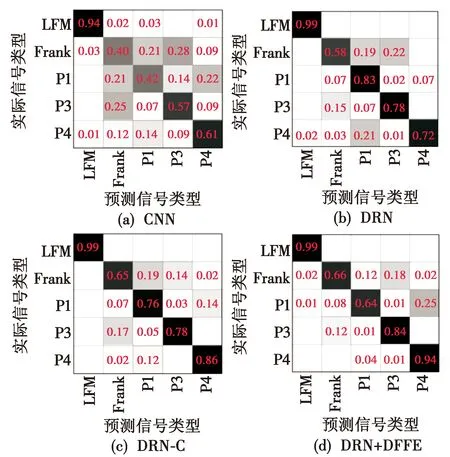
图8 不同模型方法的5类信号混淆矩阵Fig.8 5 types of signal confusion matrixof different methods

由图8可见，Frank码与P3码、P1码和P4码等信号容易混淆，由于这几种信号的时频特征相似，其区别主要为时频脊线的细微特征变化，所以导致误识别。

本文所提方法在信噪比为-10 dB时对LFM、Frank码、P1码、P3码、P4码信号的识别准确率为82.1%，高出CNN约20%，高出DRN约3%，高出DRN-C约1.1%。验证了DRN+DFFE模型的优势，能够减少网格伪影现象，充分利用扩张卷积的优点，有效增大感受野，提高特征图的分辨率；加入DFFE模块能够获取更多微小特征信息，有利于提高信号的识别准确率，在低信噪比条件下对具有相似特征的信号仍具有较好识别准确率。

4 结束语

本文提出了一种基于扩张残差网络的雷达信号识别方法，利用加权平均融合算法对CWD变换、PWVD变换以及SPWVD变换进行处理，从而得到高质量特征图，设计了一种新的网络框架，将扩展残差网络与特征融合提取模块相结合，该方法结合了特征提取、特征融合及扩张卷积的优点，可以有效解决传统网络特征提取不充分的问题。仿真结果表明，与经典网络模型相比，本文方法具有更高的识别准确度，尤其在低信噪比条件下，性能优势更为明显。