基于自适应时序分解的空气污染物浓度预测
凌德森,王晓凯,朱 涛
(山西大学 物理电子工程学院,山西 太原 030006)
随着城市化和工业化的快速发展,能源需求量不断增加,大量的污染物被排放到大气中,导致了严重的空气污染问题[1]。空气污染物浓度的超标可能会诱发呼吸系统病变等疾病,进而制约社会、经济的发展[2]。因此,建立一个准确可靠的空气污染物浓度预测模型对人们规避空气污染危害和政府制定减排政策具有重要意义。
空气污染物浓度预测是一个复杂的非线性问题,目前,其研究方法分为确定性模型、统计模型和神经网络预测模型三类[3]。确定性模型是以空气动力学理论和物理化学过程为基础,通过模拟大气的物理和化学环境对空气污染物浓度进行预测[4]。最常使用的方法是高斯模型[5]和多尺度空气质量模型[6]。然而,确定性模型需要关于污染物来源以及大气的物理化学特征的可靠信息,数据不便收集,并且需要大量时间来完成预测[7]。相比较于确定性模型,统计模型更简单、更快捷、更有效,常使用的方法有自回归综合移动平均模型[8](Autoregressive Integrated Moving Average Model,ARIMA)和多元线性回归[9](Multiple Iinear Regression,MLR)。人工智能的发展为空气污染物浓度预测研究提供了新的机会。当人工神经网络(Artificial Neural Network,ANN)被证明在污染物浓度的预测上能够取得良好的性能后[10],ANN被广泛应用于空气污染物浓度预测中[11]。然而,人工神经网络存在难以提取时间序列和相关的时序特征问题[12]。随后递归神经网络(Recurrent Neural Network,RNN)的出现在一定程度上解决了该问题,并在时序问题的分析中表现出更强的适应性。长短期记忆(Long-Short Term Memory,LSTM)网络是RNN的一种变体,具有特殊的门结构加强了数据间长期依赖关系的获取,解决了RNN在训练过程中的梯度消失问题以及无法获取数据之间长期依赖关系[13]的问题。门控循环单元(Gated Recirculation Unit,GRU)神经网络是LSTM网络的进一步改进,在具有LSTM神经网络相同效果的同时降低了网络结构的复杂度。空气污染物浓度序列是典型的非线性、非平稳时间序列,若将收集到的数据直接进行预测实验,会使得模型预测精度不高。于是丁子昂等[14]采用补充总体经验模态分解(Complementary Ensemble Empirical Mode Decomposition,CEEMD)方法将PM2.5浓度序列进行分解,并利用皮尔逊相关(Pearson)算法进行筛选,增强了数据中体现的时序特征,做到了快速、有效地预测PM2.5浓度。Jin等[15]提出一种混合深度学习模型,利用经验模态分解(Empirical Mode Decomposition,EMD)算法和卷积神经网络(Convolutional Neural Network,CNN)对PM2.5浓度数据进行分解和分类,实验结果表明,经过数据处理,可以提高预测的准确性。
因此,为了提高模型预测精度,本文采用自适应完整集成经验模态分解(Complete Ensemble Empirical Mode Decomposition with Adaptive Noise,CEEMDAN)、排列熵(Permutation Entropy,PE),以及GRU神经网络组合的空气污染物浓度预测模型。CEEMDAN算法将空气污染物浓度数据分解为不同尺度的子序列,利用PE算法计算分解后的子序列复杂度,按子序列复杂程度重新组合成新的子序列,降低模型的运算规模,最后利用GRU神经网络对重新组合后的新序列进行预测,以提高模型对空气污染物浓度的预测精度。
1 理论方法及预测模型构建
1.1 CEEMDAN分解算法
EMD是由Wu和Huang提出的一种用于处理非平稳、非线性序列的时空分析方法[16],可以在不知道的任何先验知识的情况下,依据序列自身时间尺度特征来进行信号的自适应分解处理。EMD算法分解步骤如下。
① 在给定的时间序列x(t)中,找到其所有的极值点,分别拟合极大值点和极小值点的包络线xmax(t)和xmin(t),并计算出极值点包络线的平均值x(t),再用时间序列x(t)减去平均值m(t),即得到本征模态。
h(t)=x(t)-m(t)
(1)
② 判断h(t)是否满足极值点包络平均值为零,局部极值点和过零点的数目相差在1以内,若满足则h(t)即为序列的本征模态,否则,重复步骤①直到h(t)满足条件为止。
③ 重复步骤①和步骤②,直到时间序列x(t)分解剩余的残差分量r(t)为单调序列或常序列为止。这样可得到经过EMD算法分解后的时间序列x(t)。
(2)
式中:N为分解得到的子模态数。
CEEMDAN算法是在EMD算法的基础上改进得到的,不仅拥有对非线性信号的自适应分解特性,即能够根据非线性序列自身的特征进行信号的自适应分解,而且解决了EMD 算法分解中存在的模态混叠问题。算法分解具体步骤如下。
① 在待分解的污染物浓度时间序列y(t)中,加入正负成对的高斯白噪声(-1)qεwn(t)(q=1,2),得到新序列x(t)。
x(t)=y(t)+(-1)qεwn(t)
(3)
式中:ε为白噪声的标准差;wn(t)为标准正态分布的高斯白噪声。
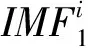
(4)
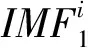
③ 对得到的N个本征分量进行平均得到CEEMDAN分解后的第一个本征模态分量:
(5)
④ 计算去除第一个本征模态后的残差序列为
(6)
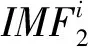
(7)
⑥ 对步骤⑤中得到的本征模态进行平均得到CEEMDAN分解后的第2个本征模态分量:
(8)
⑦ 计算去除第二个本征模态后的残余序列为
(9)
⑧ 同理,由上述步骤①~步骤⑦可以得到第k个残差序列和第k+ 1个子模态。
(10)
(11)
⑨ 重复步骤①~步骤⑧,当残差序列为单调函数时,无法再分解出新的子模态,算法结束,此时原始序列为
(12)
式中:K为最终得到的本征模态数量;R(t)为分解剩余残差分量。
1.2 排列熵算法
PE算法是一种通过比较时间序列中相邻时间点的值,来检测时间序列动态变化的方法,可以表征信号的复杂性以及度量信息的不确定性,适合处理非线性问题。PE值的大小代表时间序列的复杂性和随机性,值越大说明时间序列的复杂性越大、随机性越强;反之,时间序列随机性越弱,复杂性越小。其基本算法如下:
① 对给定的N长时间序列{X(i),i=1,2,…,N}进行相空间重构,得到相空间矩阵为
(13)
式中:j=1,2,…,K;m为嵌入的维数;τ为延迟时间;K=N-(m-1)τ。
② 将重构得到的相空间矩阵中的第j个重构分量x(j),x(j+τ),…,x[j+(m-1)τ]按数值大小进行升序排列,j1,j2,…,jm为重构分量中各元素所在列的索引。即:
x[i+(j1-1)τ]≤x[i+(j2-1)τ]≤…≤x[i+(jm-1)τ]
(14)
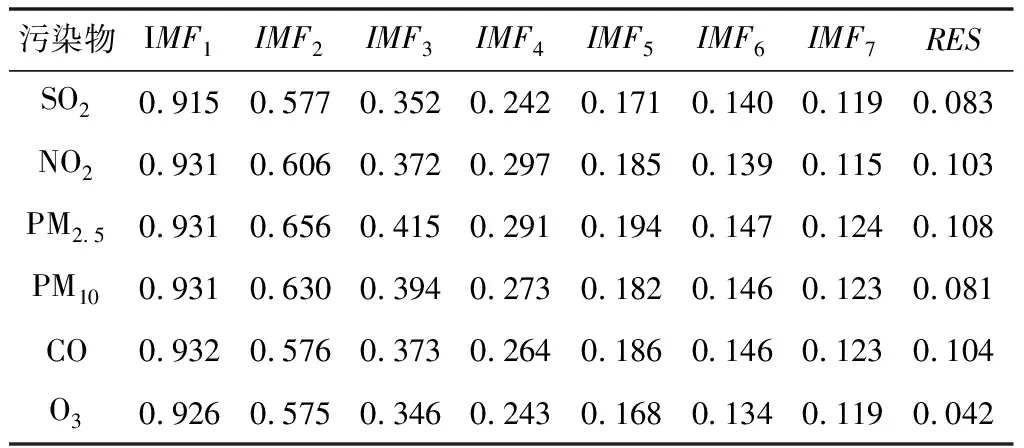
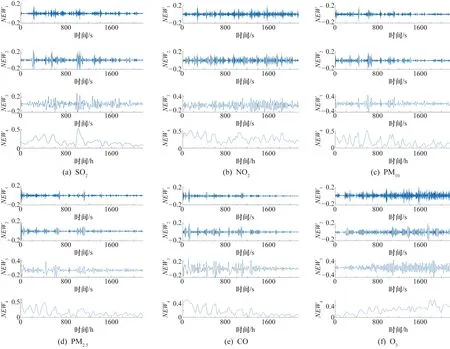
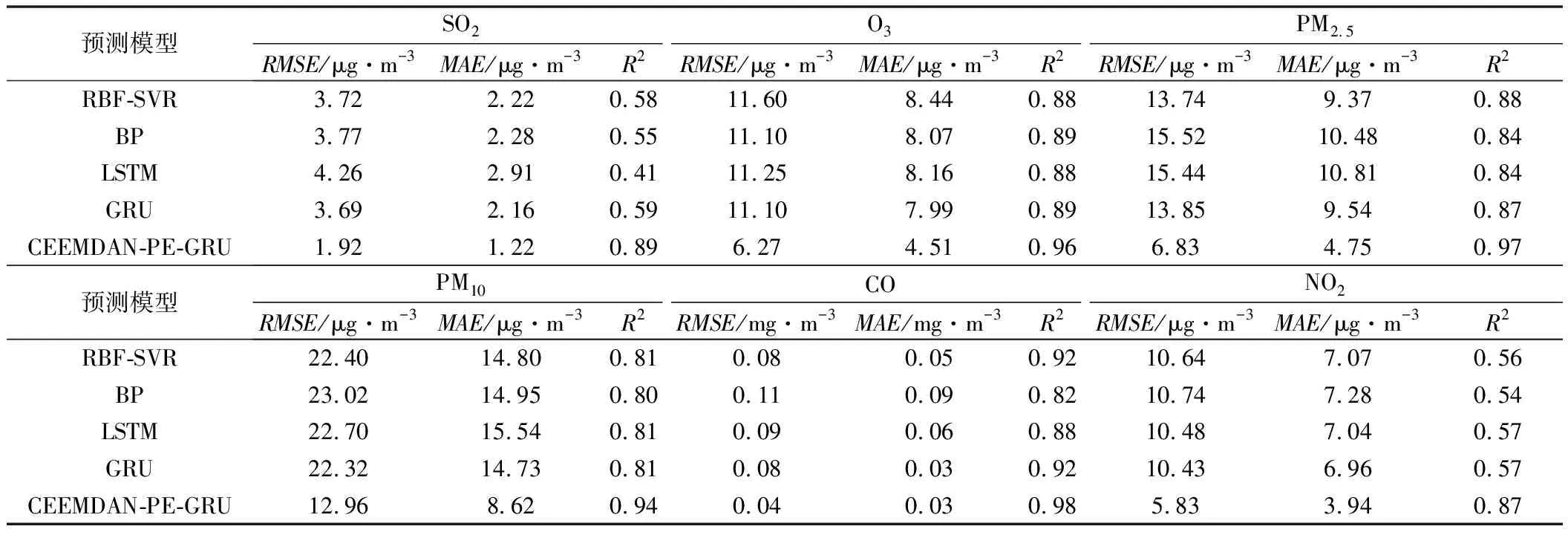
上式中重构分量中存在相等的值,则按照j1,j2的排列顺序进行大小排序,即当j1 ③ 时间序列X(i)经过相空间重构后所得的重构矩阵中的每一行都能得到一组符号序列。 S(k)=(j1,j2,…,jm) (15) 式中:k= 1,2,…,l,且k≤m!。 ⑤ 最后根据信息熵的定义,将时间序列X(i)的PE定义为 (16) 式中:0≤HPE≤ln(m!);当Pk=1/m!时,HPE达到最大值ln(m!)。 RNN是一种人工神经网络,其中网络节点之间的连接沿着序列形成有向图,因此RNN改变了传统神经网络无法保存过去数据间的相互作用的缺点,并可以显示随时间序列变化的动态行为。但是随着时间间隔的增大,RNN也变得易丢失远处的数据单元信息,即产生梯度消失的问题。为了解决RNN处理时间序列的梯度消失问题,相继提出LSTM和GRU等神经网络结构来避免产生梯度消失问题。LSTM通过输入门控制是否将数据写入细胞状态中,遗忘门控制记忆单元值的更新,输出门决定是否将值输出[17]。其中输入门计算式为 it=σ(Wi·[ht-1,xt+bf]) (17) (18) (19) 式中:xt为输入变量;Ct为细胞状态;Wi和Wc为输入偏置;σ和tanh为激活函数;σ为sigmoid函数。 遗忘门用来确定t-1时刻的隐藏状态ht-1和t时刻有多少输入的信息被保留,其公式为 ft=σ(Wf·[ht-1,xt]+bf) (20) 式中:Wf为遗忘门的权重矩阵;bf为遗忘门的偏置项。 输出门用来控制输出单元的隐藏状态是否输出,其公式为 ot=σ(Wo·[ht-1,xt]+bo) (21) ht=ot·tanh(Ct) (22) 式中:ot为输出门的输出;Wo为输出门的权重;bo为输出门的偏置项。 LSTM在3个门的相互作用下不仅能够进行长期记忆,还解决了CNN的梯度消失问题。但由于LSTM结构较为复杂,在序列的预测中效率较低,GRU神经网络是Chung等[18]在2014年提出的一种新的RNN变体,在保证与LSTM的相当精度的同时还提高了效率。GRU神经网络单元结构如图1所示。 图1 GRU神经网络单元结构 GRU摆脱了细胞状态并使用隐藏状态来传输信息,只包含两个门,分别为重置门rt和更新门zt,更新门用于控制前一时刻有多少状态信息传入到当前时刻状态,更新门的值越大,表明上一时刻状态信息传入到当前时刻的状态信息越多;重置门用来筛选信息,决定前一时刻的状态信息有多少被忽略,重置门的值越小,说明前一时刻的状态信息传入到当前时刻的状态信息越少[19]。GRU网络前向传播公式为 rt=σ(Wr·[ht-1,xt]) (23) zt=σ(Wz·[ht-1,xt]) (24) (25) (26) 基于CEEMDAN、PE和GRU组合的空气污染物浓度预测模型,在网络结构的搭建中,经过反复实验,最终得到空气污染物浓度预测模型。该模型具体步骤如下。 ① 获取空气污染物浓度历史数据,为了提高模型的预测精度、降低运算的复杂度,对原始数据进行归一化处理,公式为 (27) 式中:yi为归一化后的污染物浓度历史实时数据;xi为原始数据;xmax、xmin分别为原始数据中的最大值、最小值。 ② 利用CEEMDAN分解算法将归一化后的污染物浓度数据进行分解,获得一组固有模态函数{IMF1,IMF2,…,IMFn}分量和一个残余分量RES。 ③ 利用PE算法计算出②中得到的{IMF1,IMF2,…,IMFn}分量以及RES分量的PE值,并按照PE值的大小将各分量重新组合成新的子序列{NEW1,NEW2,…,NEWm}。 ⑤ 将各子序列预测结果叠加,并进行反归一化处理得到最终的预测结果。 CEEMDAN-PE-GRU预测模型结构如图2所示。 图2 CEEMDAN-PE-GRU预测模型结构 本文的研究目的是能够精确预测空气污染物浓度的变化趋势。为了能够更好地衡量模型的预测效果,采用了3个评价指标来分析预测结果与真实值之间偏差[20]:平均绝对误差(Mean Absolute Error,MAE)、均方根误差(Root Mean Squared Error,RMSE)和决定系数(Coefficient of Determination)。一般来说RMSE和MAE值越小,决定系数的值越接近1,则预测结果与真实值之间的偏差越小,模型的拟合效果越好;反之,则偏差较大、模型的拟合效果越差。计算公式为 (28) (29) (30) 为了得到有效的预测精度,对不同的GRU网络层数的模型进行了实验,将污染物浓度序列作为验证实验对象,选择单隐藏层、双隐藏层和三隐藏层进行实验,实验结果如表1所示。由表1中的结果可知:隐藏层数的增加并不一定可以带来更好的预测效果。因此,经过多次实验,本文最终选择使用单隐藏层神经网络进行预测。 表1 不同层数网络的实验结果 网格搜索法是指定参数值的一种穷举搜索方法,该方法将预测模型的参数通过交叉验证方法进行优化,来获取最优的学习算法。 为了减少模型预测过程中出现的过拟合或欠拟合问题,保证模型的最优化,使用网格搜索算法进行预测模型参数的选取;为了保证各模型实验的公平性,所有实验过程均在相同的硬件环境下,并利用MATLAB2019b和Python3.6仿真平台搭建预测模型。综上,预测模型以及对比模型主要参数如表2所示。 表2 预测模型及对比模型主要参数 本文选择以某市2017年1月1日至2017年3月31日,每小时采样一次的空气污染物浓度数据为研究样例。数据集收集于中国环境检测总站的全国城市空气质量实时发布平台(https://air.cnemc.cn)和真气网(https://www.aqistudy.cn/),其中包括PM10、PM2.5、SO2、NO2、O3和CO六项主要污染物浓度,共2160条数据。各污染物浓度时间序列如图3所示。为了验证模型对污染物浓度的预测性能,将各污染物数据的前1952条数据作为预测模型的训练集,后208条数据作为测试数据集。 图3 空气污染物浓度时间序列 由于空气污染物浓度序列具有典型的非平稳性、非线性特点,本文利用CEEMDAN算法对非线性序列的自适应分解特性,将归一化后的原始空气污染物浓度序列进行分解,各污染物浓度序列分解结果如图4所示。 图4 基于CEEMDAN的污染物浓度分解结果 若将分解后的分量分别进行预测,会增大预测模型的计算规模,因此为了降低模型的计算规模,以及更有效地对空气污染物进行预测,采用PE算法对分解得到的各分量进行计算,以此评估各分量的复杂程度。各污染物浓度序列分量PE值如表3所示。 表3 各污染物浓度序列分量PE值 如图4所示,污染物浓度序列IMF分量的波动性逐渐降低,深刻体现了污染物浓度在3个月内波动趋势的变化,RES体现了空气污染物浓度的变化趋势。另外结合表3可以看出,IMF1、IMF2的复杂度最大,且随机性较强,虽然两者相邻,但PE值相差较大,因此将IMF1、IMF2分别作为单独序列;IMF3和IMF4的波动相似且具有一定的规律性,PE值在0.2~0.5之间,故将其合并成一个新的序列;IMF5~IMF7不仅数据变化平稳,而且具有相对较高的规律性,RES作为污染物的变化趋势,其平稳性高、波动简单,因此将IMF5~IMF7和RES合并为新序列。重组后的新序列如图5所示。 图5 重组后的新序列 为了验证本文预测模型的优越性,在相同的计算环境下分别建立CEEMDAN-PE-GRU模型、BP模型、LSTM模型、GRU模型和经过径向基函数(RBF)改进的SVR模型对PM2.5、PM10、NO2、O3、CO和SO2共6项污染物分别进行仿真分析。各模型对污染物的预测结果与真实数据对比如图6所示,各模型预测性能对比指标结果如表4所示。 如图6所示,BP模型、LSTM模型、GRU模型和RBF-SVR模型的预测结果与真实结果有着较大的误差,总体结果存在较大的滞后性;而CEEMDAN-PE-GRU模型虽然在部分变化复杂的位置上也存在一定的误差,但总体预测结果与真实值最接近、滞后性更低,能够更准确地反映污染物的变化趋势,较其他4种模型的预测结果来说效果更好。 图6 各污染物预测结果 如表4所示,相比较BP模型、LSTM模型和RBF-SVR模型,GRU模型预测结果的平均绝对误差、均方根误差有着不同程度的降低,决定系数增加,表明GRU神经网络能够更好地对空气污染物浓度时间序列进行预测。与RBF-SVR模型、BP模型、LSTM模型以及GRU模型相比较的结果来看,基于CEEMDAN-PE-GRU模型的平均绝对误差、均方根误差和决定系数都优于其他4种模型。以空气污染物中SO2浓度的预测结果为例,就CEEMDAN-PE-GRU模型与其他4种模型的均方根误差而言,分别下降了48.38%、49.07%、54.92%和47.96%,说明CEEMDAN-PE-GRU模型预测精度最高、误差最小;另外与单一GRU模型比较可以得出,经过CEEMDAN-PE处理后的预测模型的精度明显提高,其平均绝对误差、均方根误差分别下降了43.51%、47.96%,决定系数增加了50.84%,表明经过CEEMDAN-PE处理后的预测模型能够更好地挖掘数据中的隐藏信息,实现更加精确的预测。 表4 不同模型预测性能比较结果 综上所述,CEEMDAN-PE-GRU模型对空气污染物浓度的预测具有更高的精度,优于RBF-SVR模型、BP模型、LSTM模型和GRU模型。 为了提高对空气污染物浓度的预测精度,降低序列的非线性、非平稳波动特性的影响,基于CEEMDAN-PE-GRU模型,对6项空气污染物浓度数据进行研究,结果表明利用CEEMDAN分解算法对空气污染物浓度序列进行分解可以有效地挖掘数据中的变化规律和隐藏信息,其次使用PE算法将复杂度相近的子序列进行重构,达到挖掘隐藏信息的同时降低了组合预测方法的计算规模。通过与RBF-SVR模型、BP模型、LSTM模型和GRU模型相比,本文预测模型各项指标都优于其他模型,表明CEEMDAN-PE-GRU模型能够更好地处理空气污染物浓度序列,提高空气污染物浓度的预测精度。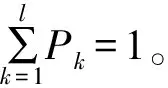
1.3 GRU神经网络
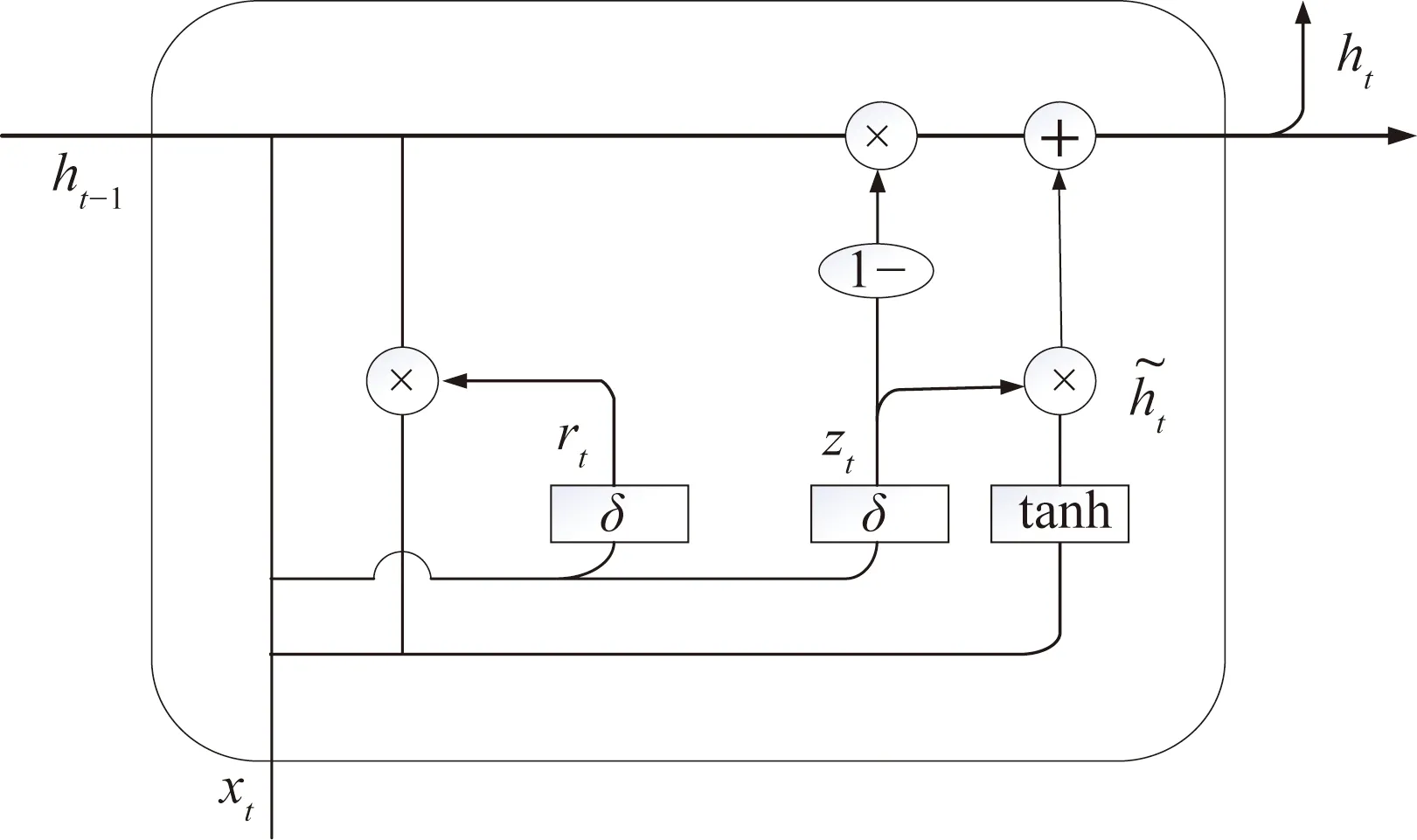
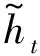
1.4 预测模型构建
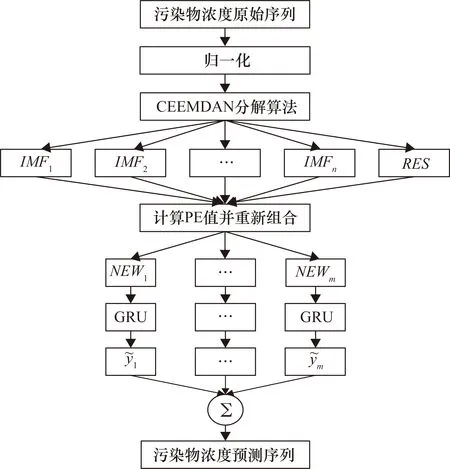
1.5 预测模型的评价指标
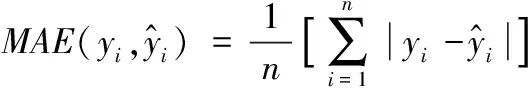
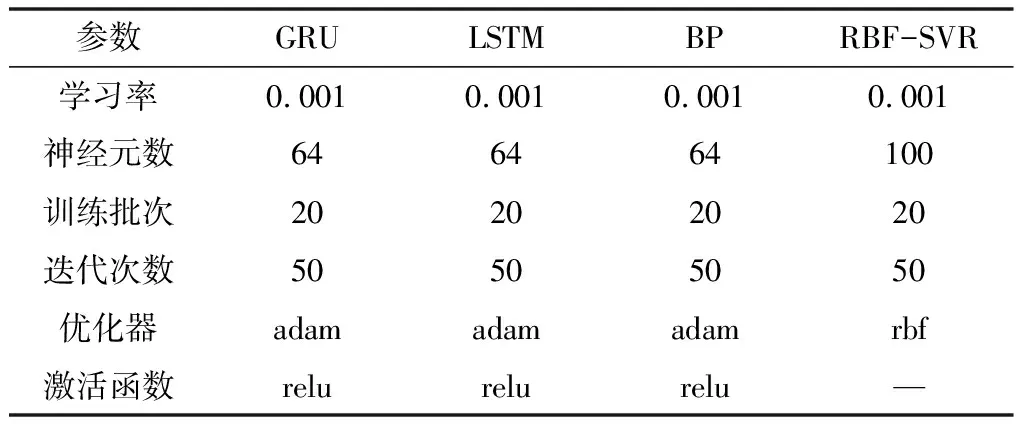
1.6 模型参数的选取

2 实验与结果分析
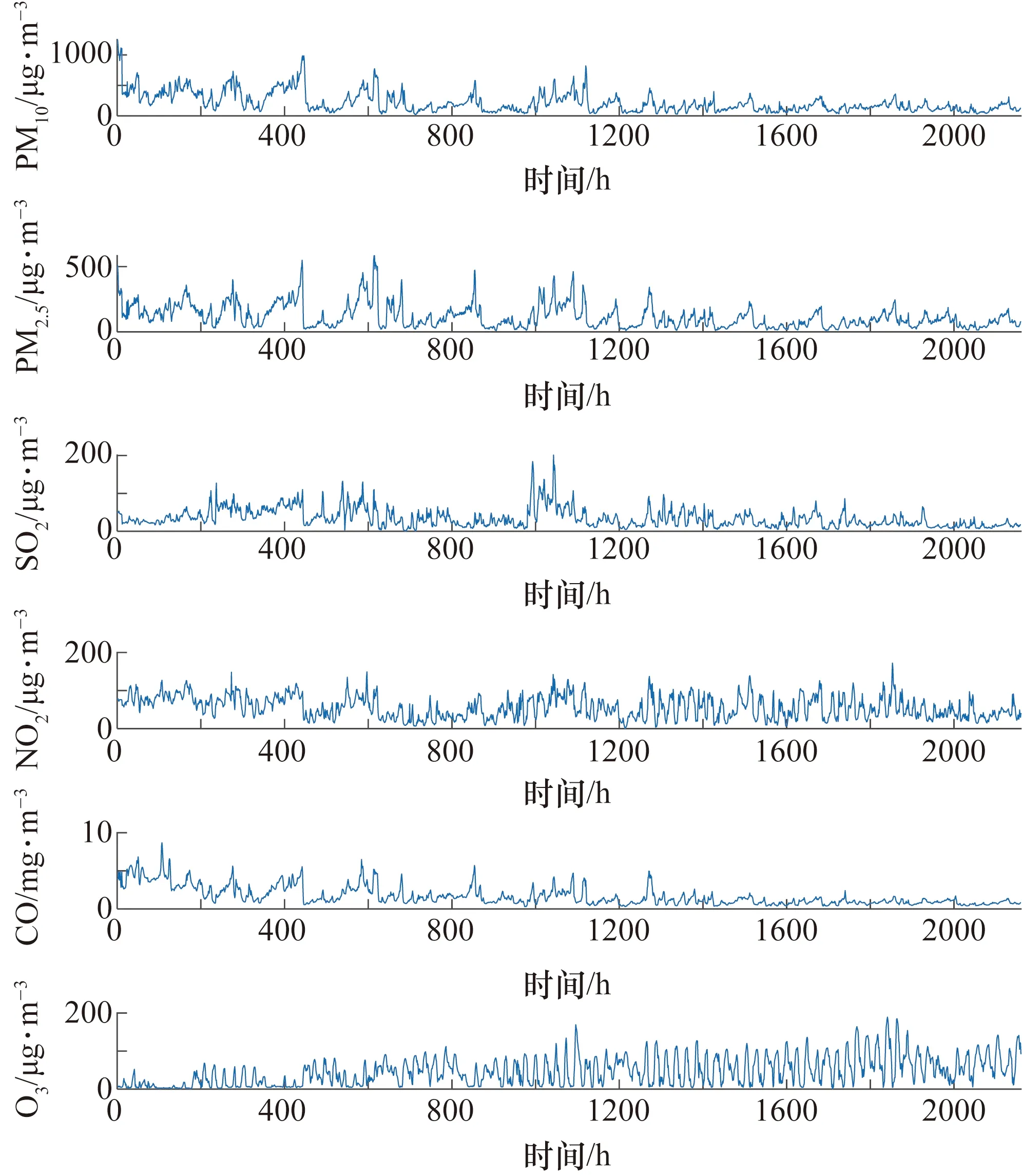
2.1 数据来源
2.2 数据分解与重组

2.3 预测结果与分析

3 结束语

