低高度极尖区位形的经验模式

刘子谦，李 晖,2*，王 赤,2，韩金鹏，王江燕

1 中国科学院国家空间科学中心 空间天气学国家重点实验室，北京 100190

2 中国科学院大学，北京 100049

3 中国运载火箭技术研究院，北京 100076

0 引 言

极尖区位于高纬度日侧磁层中，是一个充满了太阳风等离子体的狭窄“漏斗”形区域，从磁层顶上的一个“凹陷”一直延伸到地球磁极附近的电离层足点.由于南向行星际磁场（interplanetary magnetic field, IMF）BZ造成的日侧磁层顶重联（Reiff et al., 1977）和北向IMFBZ造成的高纬重联（Luhmann et al., 1984），太阳风等离子体可以通过极尖区直接进入内磁层和电离层.极尖区是太阳风进入磁层、电离层系统的通道，准确刻画其位形特征对于空间天气预报和科学研究都很重要.

自1970年代以来，基于不同的卫星观测数据和极尖区判断方法，学者们研究了上游太阳风条件和地磁倾角对极尖区位置和宽度的影响.从卫星观测来确定极尖区位形并不是一件容易的工作，常见的判断特征包括离子色散特征（Reiff et al., 1977;Rosenbauer et al., 1975; Trattner et al., 2005）、地磁场总磁场减小（Palmroth et al., 2001a; Zhou and Russell, 1997; Zhou et al., 1999, 2000）、离子相对密度增强（Newell and Meng, 1988; Palmroth et al.,2001a; Peterson and Trattner, 2012）以及强烈的静电波和电磁波等，而且这些特征通常不会同时满足.

研究发现，极尖区位形主要受IMFBZ的影响.极尖区的磁场线平均曲率半径在北向IMFBZ时为19.75RE，而在南向IMFBZ时为5.13RE（Xiao et al., 2018），极尖区极光强度也小于北向IMFBZ时（Qiu et al., 2022）.南向IMFBZ增大，极尖区以0.7o～1o/nT 的速率向赤道移动，两者存在明显的线性关系（Burch, 1972, 1973; Carbary and Meng,1986; Li et al., 2012; Newell et al., 1989）.由于IMFBZ的不同，极尖区地磁纬度（geomagnetic latitude,MLAT）在70o～86o之间变化（Zhou and Russell,1997; Zhou et al., 2000）.极尖区向赤道移动时，极尖区低纬边界的移动速率小于高纬边界，造成极尖区在MLAT 方向上的宽度减小，变化率为0.052o/nT 左右（Escoubet and Bosqued, 1989; Pitout et al., 2006）.相对于MLAT 宽度，极尖区的磁地方时（local magnetic time, MLT）宽度随IMFBZ的变化更显著.由于IMFBZ的变化，MLT 宽度可以从2 小时增大到4 小时，在极端地磁活动时甚至能达到8 小时（Crooker and Burke, 1991; Li et al.,2012; Merka et al., 2002; Newell et al., 1989）.

太阳风动压（dynamic pressure,PD）也会影响极尖区的位置和宽度.PD增加，极尖区向赤道方向移动，低纬边界移动速率大于高纬边界，进一步造成MLAT 宽度增大（Li et al., 2012; Palmroth et al.,2001b; Pitout et al., 2006）.随着PD的变化，极尖区的MLAT 宽度的变化范围为1o～4o（Burch,1972, 1973; Zhou et al., 2000）.

IMFBY主要影响极尖区MLT，东向IMFBY时极尖区向昏侧移动，西向IMFBY时向晨侧移动，MLT 的变化范围为11～13 时（Li et al., 2012；Merka et al., 2002）.BX和地磁倾角也会影响极尖区的MLAT.随着BX负向增大，极尖区在北向BZ时将向极区移动，而南向BZ时则向赤道略微移动，而BX正向变化则基本不影响极尖区（徐佳莹等,2018）.地磁倾角为0o时，极尖区MLAT 约为80o（Zhou et al., 1999）.地磁倾角每向太阳倾斜15o左右，极尖区向两极移动1o，并且随着高度增加，随地磁倾角的变化更明显（Guo et al., 2013; Merka et al., 2002; Newell et al., 1989; Palmroth et al.,2001b）.

此外，一些太阳风磁层耦合函数也被用来预测极尖区的位置，如ε函数、VBS电场、Kan-Lee 电场（Kan and Lee, 1979; Perreault and Akasofu, 1978）等.对比发现，最佳耦合函数是电场，例如VBS（V 是太阳风速度，BS是南向BZ）、Kan-Lee 电场EKL=VBTsin2(θc/2)（BT是YZ 平面中的IMF 分量，θC是IMF 时钟角），以及它们的中间函数EWAV=VBTsin4(θc/2)，比IMFBZ更好地提供与MLAT 的线性关系，其中EWAV是最好的（Newell et al., 2006）.

除了观测数据识别外，三维全球磁流体力学（magneto hydro dynamics, MHD）模拟也用于判断极尖区位形.Palmroth 等（2001a）根据全球磁层MHD 模拟中的磁场衰减、等离子体能量密度和开/闭场线边界确定了高高度极尖区，发现随着南向IMF 的增加极尖区向赤道移动.通过使用类似的方法，Fenrich 等（2001）进一步发现，极尖区在北向IMFBZ时位于MLAT 81o附近，南向IMFBZ时位于75o附近，在东向IMF 下极尖区向黄昏方向移动了2 MLT 左右，与Tsyganenko 和Stern（1996）、Li 等（2012）给出的结果一致.Siscoe 等（2005）使用MHD 模拟研究了不同IMF 方向的极尖区几何结构，发现随着IMF 从北转南，高高度极尖区的MLAT 减小，并且存在与IMFBY相关的晨昏不对称性.Zhang 等（2013）根据中等磁暴的磁流体力学模拟得出的磁场衰减、等离子体密度和平行离子通量确定了低高度极尖区，研究了极尖区的MLAT（MLT）和IMFBZ（BY）的相关性，发现极尖区的MLAT 和MLT 宽度随PD增加而增加.

过去的研究仅给出了极尖区位置和宽度随太阳风条件的变化，而没有给出其整体位形关于太阳风条件函数的经验模型.卫星观测只能提供沿卫星轨道的极尖区穿越，而MHD 模拟可以给出磁层所有网格的物理量，并使呈现极尖区整体位形成为可能.因为低高度极尖区位形主要受IMF 的影响变化情况比较简单，并且低高度卫星较多方便对比验证，所以本文建立低高度极尖区的经验模式，作为将来进一步工作的基础.利用2008年3月8日两个连续亚暴的全球MHD 模拟，研究低高度极尖区的位置和宽度随IMFBY和BZ的变化.在此期间，太阳风条件覆盖了线性相关分析所需的参数范围，模拟结果基本上再现了地磁场的大范围变化.然后利用椭圆函数构造了低高度极尖区位形的经验模式，可以计算不同IMF 时的低高度极尖区位形.

1 方法

本节首先介绍全球MHD 模拟模型和2008年3月8日的两次连续亚暴，然后从模拟数据中识别极尖区.

1.1 2008年3月8日事件的全球MHD 模拟

我们主要使用由Hu 等（2005, 2007）开发的全球三维分段抛物线和拉格朗日重映射PPMLRMHD 模型来模拟太阳风-磁层-电离层（solar windmagnetosphere-ionosphere, SW-M-I）耦合系统.该程序已成功地用于模拟行星际激波与磁层、磁层顶开尔文-亥姆霍兹不稳定性和大尺度电流系统的相互作用.在这项工作使用的典型模拟中，计算区域定义为GSM 坐标中的-300RE＜X＜ 30RE和-150RE＜Y,Z＜ 150RE，内边界设置为一个半径3RE的球体，以避免与地球表面附近的等离子体层和强磁场相关的复杂性.整个区域由240 ×240 ×240 的网格组成.在X，Y，Z＜ 10RE的内部区域中，均匀网格的网格间距由0.2RE组成，其他区域根据每个轴上公比为1.05 的几何级数增加.在SW-M 系统中，程序以完全守恒的形式求解MHD 方程，而在电离层中求解静电方程.磁层和电离层之间的耦合由沿地球偶极磁场的两个映射组成，包括从磁层内边界到电离层的场向电流（FAC）映射和反向电势映射.MHD方程的保守形式保证了数值模拟中质量、动量和能量的守恒.有关全球MHD 模型的其他详细信息，请参见Hu 等（2007）.

2008年3月8日10:00 世界时（universal time,UT）至22:00 UT 期间发生了两个孤立的亚暴.图1展示了来自OMNI 数据集的观测结果，包括AU/AL 指数、SYM-H 指数、行星际磁场、太阳风动压.根据AL 指数，第一次亚暴在11:30 UT 左右开始，在13:40 UT 左右达到峰值，然后开始恢复，直到15:00 UT 才恢复到平静水平.第二次亚暴大约在16:50 UT 开始，持续了3 个多小时才恢复平静.第二次亚暴的强度比第一次略弱，AL 的最小值约为-550 nT，而第一次亚暴的最小值为-850 nT.在这两次亚暴期间，最小SYM-H 指数分别为-15 nT和-35 nT，这意味着在此期间没有中等及以上级别的磁暴事件.我们之所以关注这一事件的模拟是因为它涵盖了太阳风条件的一个大参数范围的变化过程.在这次活动中，IMFBY从-10 nT 到10 nT，IMFBZ从-15 nT 到10 nT，太阳风动压从1 nPa 到15 nPa，涵盖了线性相关分析所需的一系列典型参数空间，为极尖区位形与上游太阳风条件之间的相关性分析和数据模型比较提供了良好的参数范围.

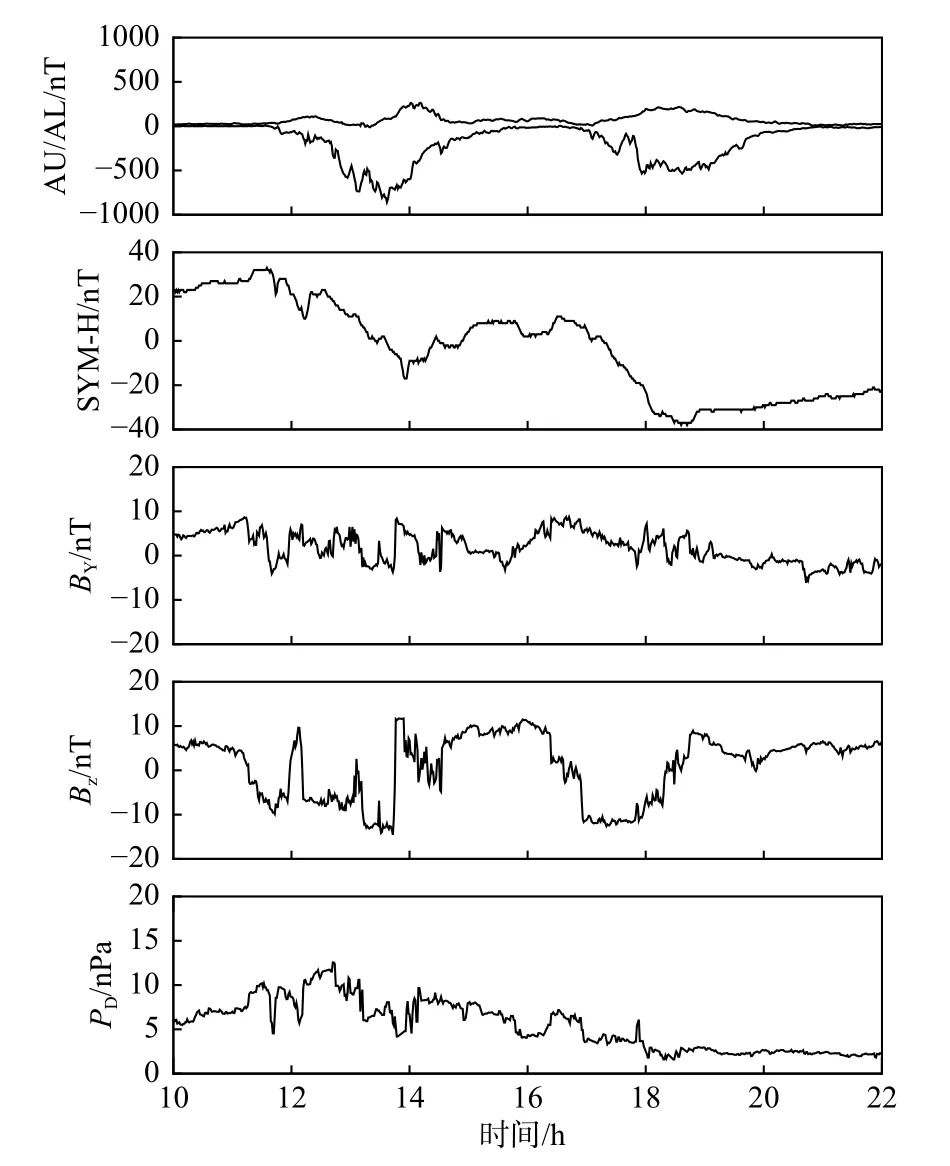
图1 2008年3月8日连续两次亚暴的概述.AU：虚线；AL：点线Fig.1 The overview of two successive substorm on 8 March 2008

1.2 极尖区中心和边界的识别

根据模拟数据得到的等离子体热压（thermal pressure,PT）用于判断半径为6RE的球面上的极尖区中心.极尖区中心定义为PT达到最大值的点.图2展示了模拟数据得出的PT在北半球的空间分布.图2a 显示12:00 UT，西向IMFBY和南向BZ，图2b 显示14:20 UT，东向IMFBY和北向BZ.很明显，在北向IMFBZ时，极尖区中心的MLAT 高于南向IMFBZ时，因为在北向IMFBZ时，磁重联发生在极尖区高纬侧，极尖区向两极移动，而在南向IMFBZ时，磁重联发生在低纬侧，极尖区向赤道移动.西向IMFBY时极尖区位于晨侧，东向IMFBY时位于昏侧，这是由IMFBY引起的日侧重联点移动造成的.

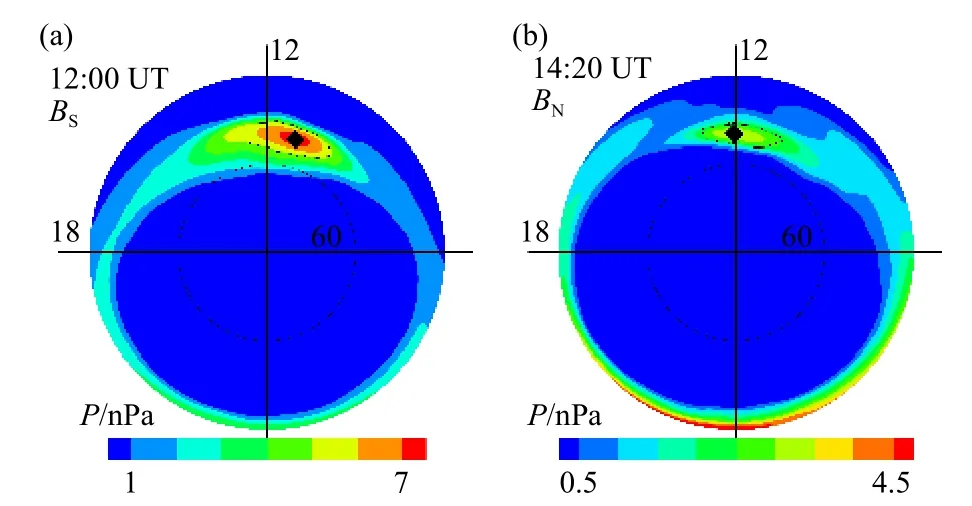
图2 北半球热压的空间分布.（a）西向IMF BY 和南向BZ；（b）东向IMF BY 和北向 BZ.菱形表示极尖区中心，实线表示极尖区边界.BS：南向BZ，BN：北向BZ，P：热压Fig.2 The spatial distribution of P on the northern hemispheric surface derived from the simulation data.The left panel shows that at 12:00 UT under dawnward IMF BY and southward BZ and the right panel shows that at 14:20 UT under duskward IMF BY and northward BZ.The cusp centers are denoted by diamonds, and the cusp boundaries are represents by solid lines

在确定极尖区中心后，确定极尖区边界.球面上的网格分为36 个扇区，每个扇区相对于极尖区中心的宽度为10o.对于每个扇区，我们将PT下降到极尖区中心的68%的位置作为极尖区边界，这个数字来自低纬度最后一条开放磁通的PT与极尖区中心的比值.因此，可以找到36 个格点，并围绕极尖区中心组成一条闭合曲线，此处定义为极尖区边界（实线）.北向BZ时的极尖区MLAT 宽度比南向BZ时的宽，与前人结果一致.除等离子体热压外，磁层衰减BT-Bdipole和场向离子通量NV·B也可用于识别极尖区.但是磁场衰减不能很好地识别极尖区边界，因为极尖区边界内外的磁场区别不太大.北向IMFBZ时，场向离子通量判断得到的极尖区中心的MLAT 略高于真实值，因为磁重联发生在极尖区高纬侧，离子流直接从重联区域流出.

选择半径为6RE的球面进行极尖区识别有两个主要原因.首先，6RE球面远离模拟内边界3RE，其中MHD 解可能会受到内边界条件的影响.其次，在典型的太阳风条件下，6RE球面位于磁层内.在极端的太阳风条件下，磁层顶有时可能会压缩至6RE球面内，此时6RE球面不再适合识别极尖区.但在本次事件中，太阳风的动压并不是很大，6RE球面保持在磁层顶内，因此6RE球面被用于整个研究.除了6RE球面之外，4～8RE球面也可以识别极尖区，并且结果几乎相同.所以球面的选择基本不影响极尖区的判断.

与高高度极尖区相比，我们更感兴趣的是更稳定的低高度极尖区.这是因为低高度极尖区的位置主要取决于开放/闭合边界，也就是说，主要取决于重联导致的日侧磁通量的侵蚀.而高高度极尖区也受到太阳风动压的影响，因为高高度的磁层磁力线可以被太阳风明显压缩，或者，磁层顶随动压的增加而向地移动，导致极尖区更靠近磁层顶.但MHD 模拟的内边界设置为3RE，仅在SW-M 系统中求解MHD 方程，而在电离层中求解静电方程，因此在低高度无法直接识别极尖区中心.幸运的是，磁层和电离层之间的耦合包括场向电流的映射和电势的映射，这两种映射都沿着地球的偶极磁力线.低高度（1.1RE高度）极尖区可由高高度极尖区通过沿磁力线绘制获得.本文中使用的低高度极尖区的坐标系是地磁坐标系.

为了确定低高度极尖区与太阳风条件的关系，我们首先选择椭圆函数来拟合判断得到的低高度极尖区：

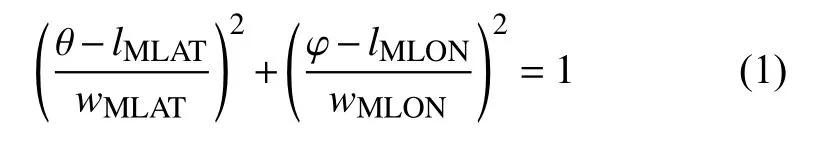
其中，θ 是极尖区边界的MLAT，为与MLAT 对应，设定相对地磁经度MLON=(MLT-12) ×15， φ是极尖区边界的MLON.lMLAT、lMLON是极尖区中心的MLAT 和 MLON，wMLAT、wMLON是极尖区的MLAT 宽度和MLON 宽度.这四个量构成了极尖区的位形参数.

图3 分别显示了北向和南向IMF 下的两个极尖区边界的曲线拟合结果，和判断结果非常匹配.在北向IMF 时，极尖区几乎是圆形的，而在南向IMF 时，极尖区是椭圆形的.图4 显示了事件期间极尖区拟合的相关系数（correlation coefficient, cc）分布.大多数相关系数大于0.8，通过90%的置信水平，平均值和中位值分别为0.85 和0.89，表明拟合是合理的.

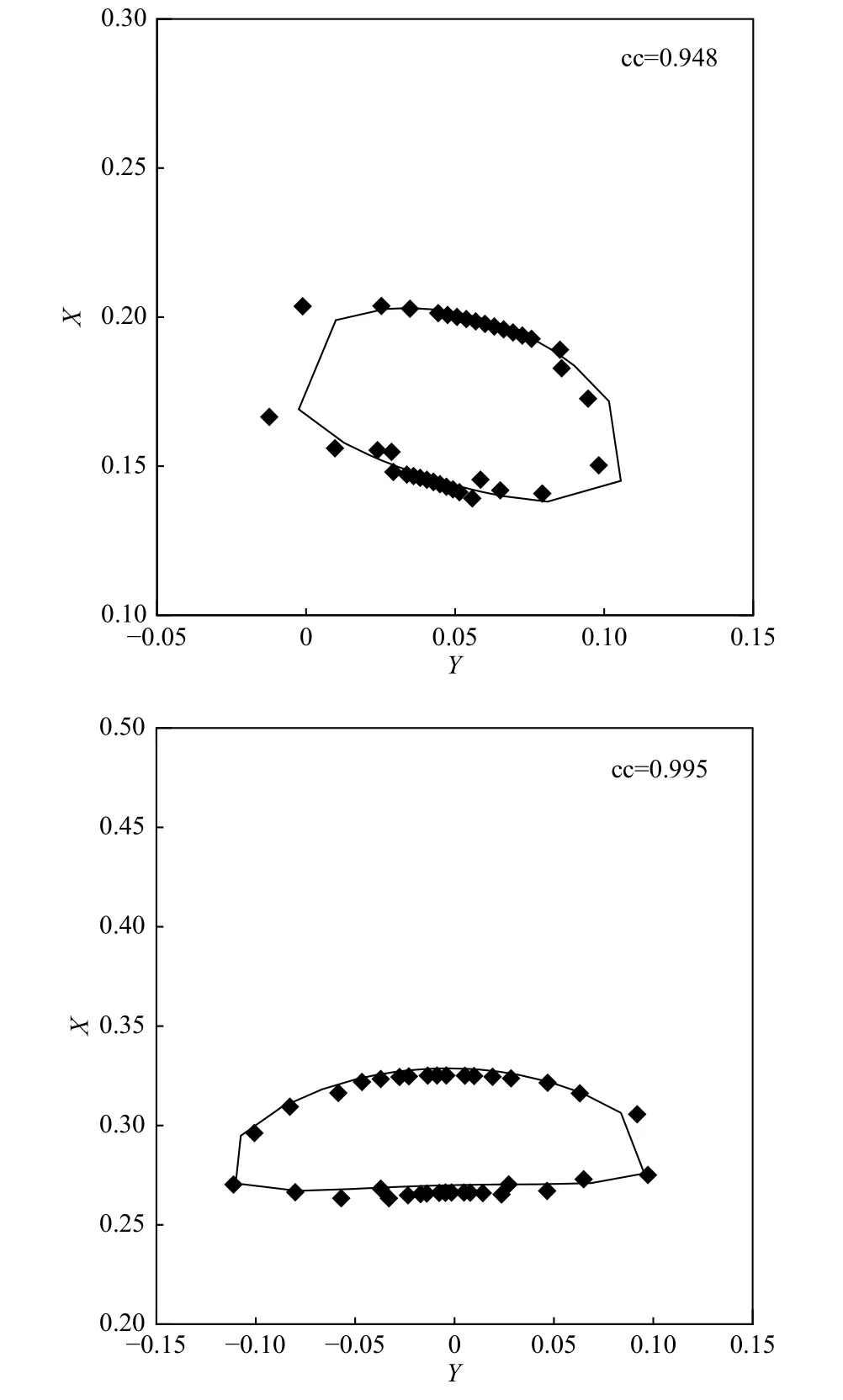
图3 北向（上）和南向（下）IMF 时，判断得到的极尖区边界（菱形）和拟合结果（直线）Fig.3 Two identified cusp boundaries (diamonds) and the corresponding curve fitting results (line) under northward and southward IMF

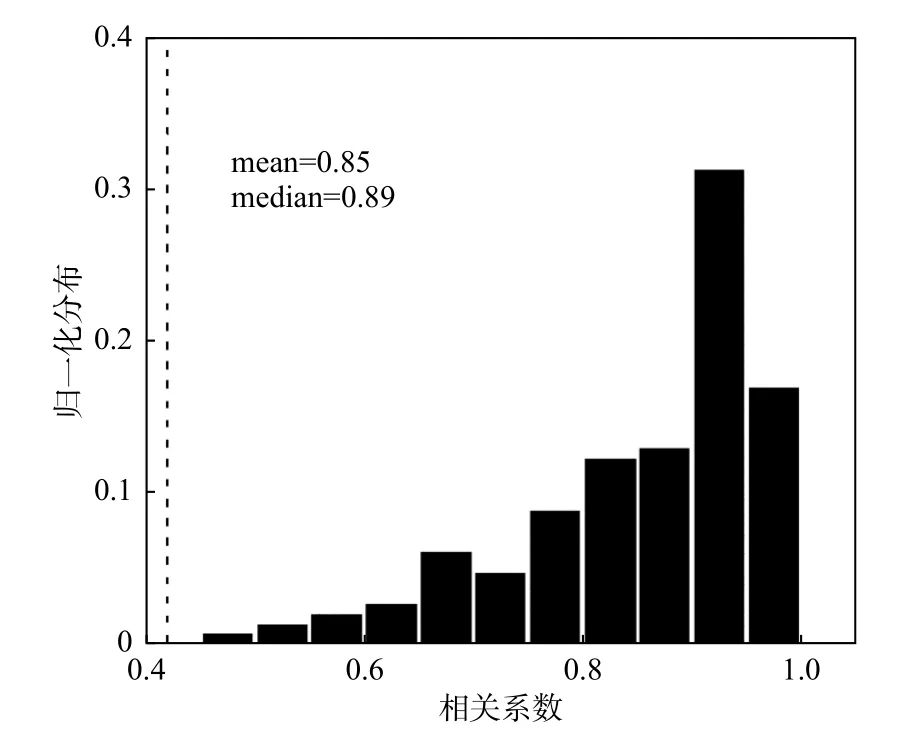
图4 事件期间极尖区拟合的相关系数分布，阈值由垂直虚线表示.mean：平均值，median：中值Fig.4 The correlation coefficient distribution of the cusp fitting during the event.The threshold value is denoted by the vertical dashed line

2 结果

本节首先研究了极尖区中心的MLAT 与IMFBZ的关系，以及MLON 与IMFBY的关系.如前所述，地磁倾角也会影响低高度极尖区，但与IMF相比，影响相对较小（Newell et al., 1989; Zhou et al., 1999）.尤其是事件周期接近3月春分，地磁倾角约等于零，所以本次模拟数据没有考虑地磁倾角的影响.然后，我们研究了MLAT 宽度和MLON宽度对IMFBZ的依赖.利用椭圆函数和极尖区位形参数，可以建立低高度极尖区的经验模式，与DMSP 卫星的观测结果非常吻合.

2.1 极尖区位置和IMF BY、BZ 的关系

由于太阳风从上游边界（XGSM=30RE）传播到内磁层和电离层，低高度极尖区对上游太阳风条件的响应是延时的.基于相关分析，选择14 min 作为上游太阳风到低高度极尖区之间的恒定平均滞后时间.lMLAT主要受IMFBZ的影响，尤其是南向BZ，lMLAT和IMFBZ之间的线性关系如下所示：

相关系数为0.81，表明线性拟合是非常合理的.

lMLON由IMFBY控制，lMLON和IMFBY之间的线性关系由下式给出：

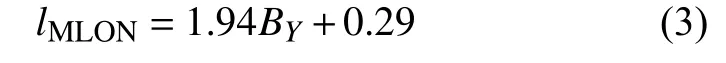
相关系数为0.69，低于lMLON和IMFBZ的相关系数，但仍然可靠.根据lMLON可以进一步计算极尖区中心的MLT：

图5 显示了我们的结果（红线）分别与Newell等（1989）、Zhang 等（2013）（黑线）的结果的比较.上图给出了极尖区中心MLAT 和IMFBZ之间的线性关系.MLAT 随北向IMFBZ的增加而逐渐增加，随南向IMFBZ的增加而显著降低.这是因为北向IMFBZ时磁重联发生在极尖区的高纬侧，极尖区将向两极移动，而南向IMFBZ时发生在低纬侧，极尖区将向赤道移动.我们的结果总体上比Newell 等（1989）的结果稍大一些.这是因为我们给出的是极尖区中心的MLAT，而Newell 等（1989）给出的是低纬边界的MLAT.下图显示极尖区中心的MLT 和IMFBY之间的线性关系.当BY=0 时，MLT 接近12，与观测结果相对应.当IMFBY为东向（西向）时，极尖区中心位于北半球黄昏（黎明）侧.这是因为在东向（西向）IMFBY时，重联点将向黄昏（黎明）移动，平行离子流主要发生在黄昏（黎明）侧.因为PPMLR 模拟的低高度极尖区首先来自6RE表面磁层等离子体的流体性质，然后沿着磁场线追踪到低高度.而观测到的极尖区直接来自DMSP 卫星低高度电离层等离子体的粒子特性，两者非常一致，表明PPMLR模拟是非常准确的.

图5 极尖区MLAT 和MLT 随IMF 的变化（红线），并与Newell 等（1989）（黑线）和Zhang 等（2013）（黑线）对比Fig.5 The comparison of our results (red line and red diamonds) with that given by Newell et al.(1989) (black line) and by Zhang et al.(2013) (black line)

2.2 极尖区宽度和IMF BZ 的关系

由于太阳风对外磁层磁力线的压缩作用比较明显，太阳风动压可以控制高高度极尖区宽度，但对低高度极尖区宽度影响较小.低高度极尖区宽度主要受IMFBZ的影响，因为低高度极尖区对应于开闭磁力线边界，主要取决于IMFBZ对日侧磁层的侵蚀.MLAT 宽度wMLAT和IMFBZ之间的线性拟合函数如下所示：

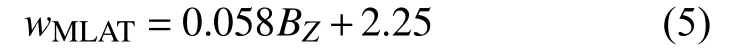
线性关系的相关系数为0.58.

MLON 宽度wMLON和IMFBZ之间的线性拟合函数为：

线性关系的相关系数为0.55.MLT 宽度（δMLT）可以如下获得：

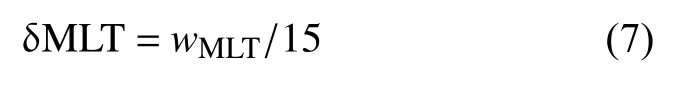
图6 显示了MLAT 宽度和MLT 宽度与IMFBZ的关系.随着IMF 由北转南，MLAT 宽度减小，变化范围为1o～4o.这是因为在南向IMF 时，极尖区的高纬和低纬边界都向赤道移动，而高纬边界的移动速度比低纬边界快.MLT 宽度随着IMFBZ由北转南而增加，变化范围为1～2 小时.这些结果与前人研究结果基本一致.

图6 MLAT 宽度和MLT 宽度随IMF BZ 的变化Fig.6 The relation of MLAT width and MLT width with IMF BZ.The red lines are the fitting Results

2.3 低高度极尖区的经验模式

在确定了位形参数lMLAT、lMLON、wMLAT、wMLON后，我们可以得到作为IMFBY和BZ函数的低高度极尖区经验模式.图7a 显示了在不同的IMFBZ时（BY=0；BZ=10 nT，0，-10 nT）我们的模式的极尖区边界.当IMFBZ由北转南时，极尖区MLAT 减小，向赤道移动；同时MLAT 宽度减小、MLON 宽度增大，极尖区椭圆离心率增大.图7b显示了在不同的BY条件下根据我们的模型计算的极尖区边界（BY=0,10 nT,BZ=-5 nT）.随着IMFBY东向增加，极尖区MLT 增加，向黄昏方向移动，而形状保持不变.这些结果与之前的研究结果一致.

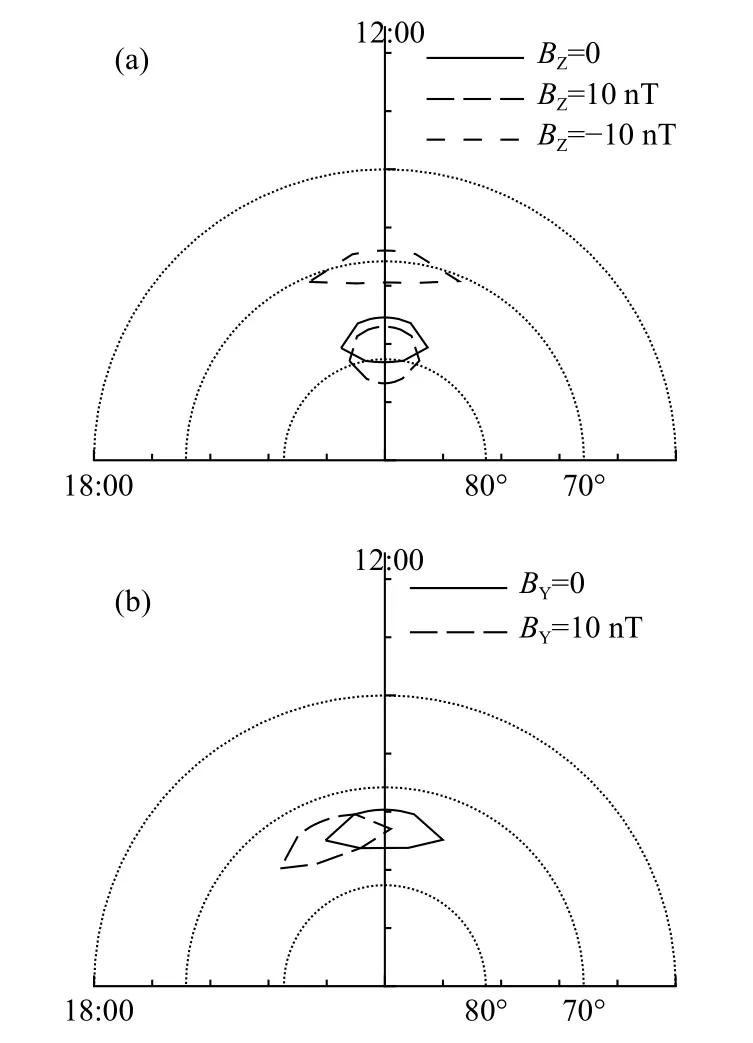
图7 IMF BZ（a）和IMF BY（b）变化时，模式计算得到的极尖区边界Fig.7 The cusp boundaries calculated from our 2-D cusp model under different IMF BZ (a) and IMF BY (b)

通过与DMSP 卫星在此事件期间的观测结果进行比较，进一步验证了我们的模式.DMSP 卫星位于太阳同步的近圆形极地轨道上，高度约845 km，轨道倾角为98.7o.除地磁高纬地区外，午后尤其是午夜后是覆盖最少的地区.所有这些卫星上的SSJ/4 仪器使用曲板静电分析仪测量电子和离子，每秒钟获得一个完整的光谱.利用Newell 和Meng（1988）首次使用的算法，评估每个单独的离子和电子光谱，来确定极尖区：（1）iave ＜ 3 000 eV；（2）eave ＜ 220 eV；（3）离子光谱通量峰值 ＞2.0×107eV/cm2s sr；并且（4）出现在100～7 000 eV之间.这里的iave（eave）是指离子（电子）平均能量.当有3 个参数满足要求时，认为进入极尖区，当有3 个参数不满足要求时，视为离开极尖区.

在本文中，利用2008年3月8日SSJ/4 静电分析仪（F13 和F15）从10:00 UT 到22:00 UT 的数据识别极尖区.为了更准确，当所有4 个条件都满足极尖区要求时，就可以作为极尖区，观测到5 个数据点位于极尖区.图8a、8b 显示了下行电子能量通量的时间变化.两个相邻的尖峰表示卫星穿过极光椭圆，菱形表示卫星穿过极尖区.很明显，两个观测到的点都位于极光椭圆中，这表明我们对极尖区的识别是合理的.图8c、8d 的右侧两图给出了模式结果和观察数据的比较.结果表明，观测到的极尖区恰好位于模式计算的极尖区的内部或附近，表明模式与观测的一致性.图9 显示了事件期间模式计算的极尖区中心MLAT（图9a）和MLT（图9b）分别与观测到的极尖区的对比.显然，观测到的极尖区的MLAT 和MLT 基本上位于模式计算的极尖区内.

图8 （a, b）从DMSP 观测到的沉降电子能量通量和观测到的极尖区（菱形）；（c, d）极尖区模式结果和对应观测结果（菱形）的比较.eeflx：下行电子能量通量Fig.8 (a, b) Time variation of the downward electron energy flux (line) and observed cusps (diamond) from the DMSP observations;(c, d) The comparison of the observed cusp (diamond) and predicted cusp (line) for the corresponding comment

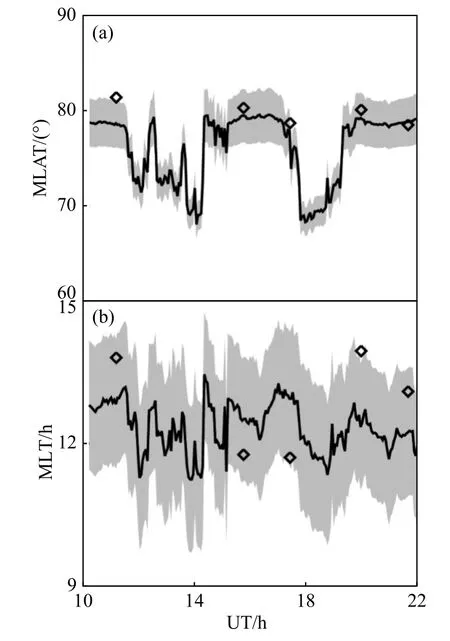
图9 极尖区MLAT（a）和MLT（b）位置（实线）和宽度（灰色区域）随时间的演化，并与DMSP 观测数据（菱形）对比Fig.9 The time variation of the predicted cusp MLAT (a) and MLT (b) location (solid line) and width (grey zone),compared with the observed cusps from the DMSP observations (diamonds)

3 讨论和结论

本文利用PPMLR MHD 全球模拟，建立了受IMFBY和BZ影响的低高度极尖区的经验模式，该模式基于2008年3月8日的事件，IMFBY从-10 nT 变为10 nT，BZ从-15 nT 变为10 nT.热压PT用于确定6RE表面上的极尖区中心和边界.极尖区中心是PT达到其最大值的位置，边界是PT降至其最大值68%的位置.为了获得低高度极尖区，沿磁力线将高高度极尖区中心和边界映射到1.1RE高度的电离层.极尖区采用椭圆函数拟合，大部分相关系数大于0.8，说明拟合是合理的.极尖区中心的MLAT 随北向BZ逐渐增加，随南向BZ大幅减少，MLT 随东向（西向）IMFBY的增加而增加（减少），BY=0 时MLT 接近正午，与前人研究结果一致.北向（南向）BZ增加，MLAT 宽度增加（减少），MLT 宽度减少（增加）.经过测试太阳风耦合函数，例如VBS、EKL和EWAV，得到了类似的结果，与Newell 等（2006）得到的DMSP 观测结果几乎一致.

根据本模式，当IMFBZ北向增加时，极尖区向两极移动并变得更圆；当IMFBZ南向增加时，极尖区向赤道移动，变得更扁.当IMFBY东向（西向）增大时，极尖区向黄昏（黎明）方向移动，形状保持不变.通过与DMSP 卫星观测到的极尖区进行比较，发现在这次事件中，观测到的极尖区正好位于模式结果的内部或附近，验证了模式的有效性.本模式可以展示低高度极尖区的位置和形状，与以前的经验结果和观测确定的极尖区一致.本模式只能展示6RE高度的极尖区横截面，并且没有考虑IMFBX、太阳风动压、地磁倾角的影响.接下来我们将利用更多太阳风条件时的数据，分析IMFBX、BY、BZ、太阳风动压、地磁倾角的影响，建立极尖区整体位形的经验模式，这将有助于空间天气预报.