Banach代数中反三角矩阵的p群逆

周心悦，刘大勇，陈焕艮

(1. 杭州师范大学数学学院，浙江 杭州 311121； 2. 中南林业科技大学理学院，湖南 长沙 410004)

0 引言

Drazin逆在众多领域中都有重要应用，而群逆作为特殊的Drazin逆被众多学者所研究.由于矩阵的实用性，许多学者对其群逆进行研究[1-3].此外，元素和与元素积的群逆也在对群逆的研究起了重要作用[4-7].与此同时，学者们对Drazin逆再进行推广，提出了广义Drazin逆,也对此进行了研究，如文献[8]. 2012年，ZHOU W和CHEN J L提出了p-Drazin逆[9].本文是对p-Drazin逆的特殊情况p-群逆进行研究，将群逆的性质推广至p-群逆.

在这篇文章中，我们考虑的是Banach 代数中的元素.对于元素a∈A，如果存在x∈A满足

ax=xa,xax=x,axa=a,

(1)

那么我们称a群可逆，x是a的群逆，记作a#.

将J(A)记作Banach 代数A 的Jacobson根.元素a∈A是p群逆的当且仅当存在x∈A使得

ax=xa,x=x2a,a-a2x∈J(A),

(2)

x称为a的p群逆，记作a×.

第1节研究了几类特殊的反三角矩阵的p群逆.第2节讨论了谱条件下，特殊反三角矩阵p群可逆性.文章中,A是有单位元的Banach代数.符号J(A)代表着A的Jacobson根.A×是A中所有p群逆的集合.

1 反三角矩阵的p群逆

在这一节中，我们讨论了几个特殊反三角矩阵的p群逆.

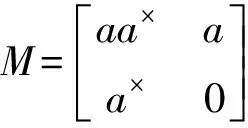
且

可证得,M是p群可逆的.

□

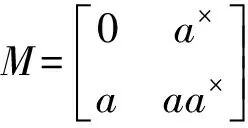
AA×=A×A,A×AA×=A×,A-A2A×∈J(M2((A)).

那么可得

MPA×P-1=PA×P-1M,

PA×P-1MPA×P-1=PA×P-1,

M-M2PA×P-1∈J(M2((A)).

(3)

故PA×P-1是M的p群逆.

□

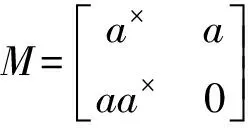
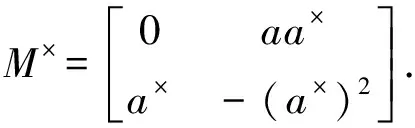
(4)

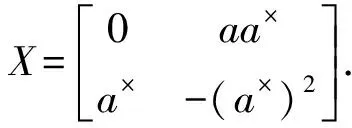
根据p群逆的定义即得X=M×.

□

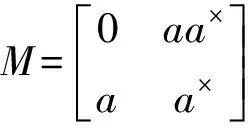
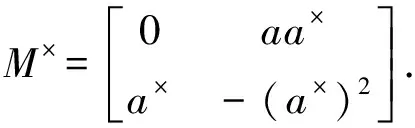
(5)

证明同推论 1的证明相似.

□

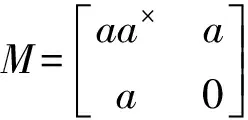
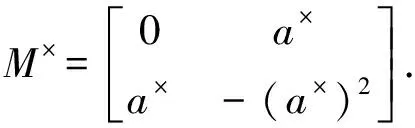
(6)

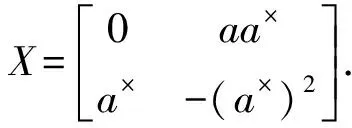
根据p群逆的定义，我们有X=M×.

□

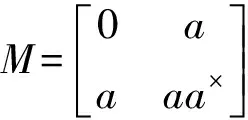
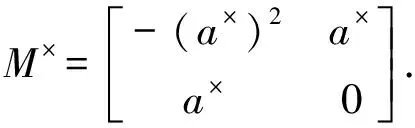
(7)

证明类似于推论 1 的证明.

□

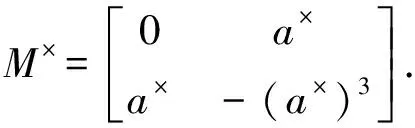
(8)

进而根据p群逆的定义，得到X=M×.

□

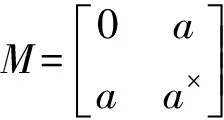
(9)

证明由定理4即得.

2 扰动条件

设p为A中的p群可逆的元，谱元素pπ=1-pp×.在这一节中，进一步讨论矩阵在扰动条件下的p群逆性质.

引理1令a,b∈A×.如果ab=0，那么a+b∈A×.这里，

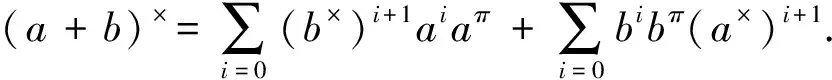
(10)

证明见[10].

□

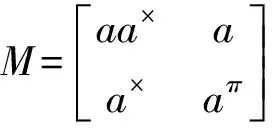
(11)

证明记M=P+Q,这里

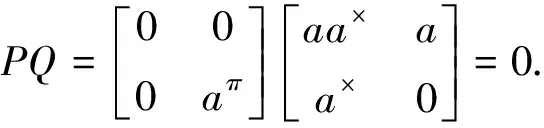
根据引理1,M有p群逆.这里，

□

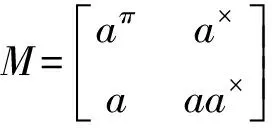
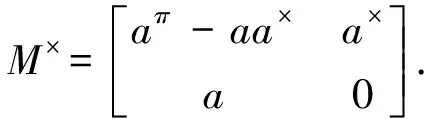
(12)

证明由定理5即得.

□

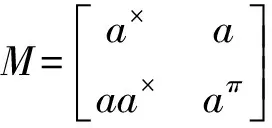
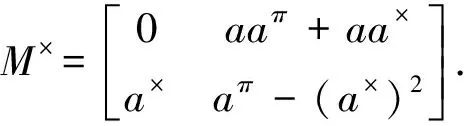
(13)

证明记M=P+Q,这里

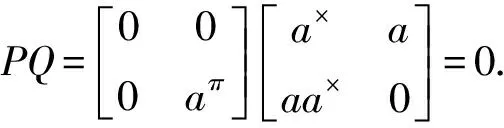
根据引理1,M有p群逆.这里，

□

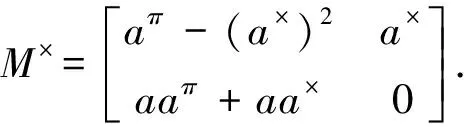
(14)

证明利用定理6得.

□

引理2令a,b∈A.如果ab∈A×,那么下列条件等价:

(1)ba∈A×;

(2)b(ab)πa∈J(A).

(ab)×=a((ba)×)2b.

那么

b(ab)πa=b(1-ab(ab)×)a=

b(1-aba((ba)×)2b)a=ba-baba((ba)×)2ba=

ba-ba(ba)×ba∈J(A).

(15)

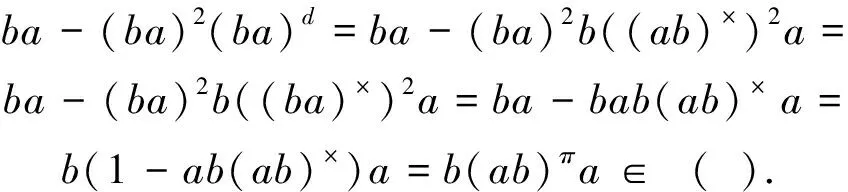
(16)

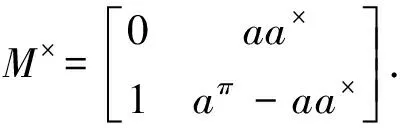
(17)

□

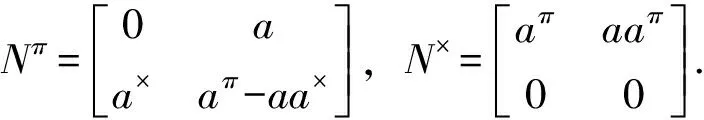
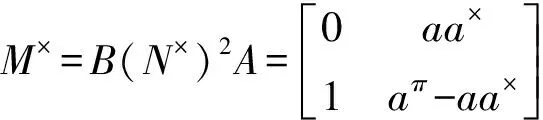
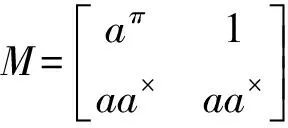
(18)

证明同推论 1的证明相似.

□

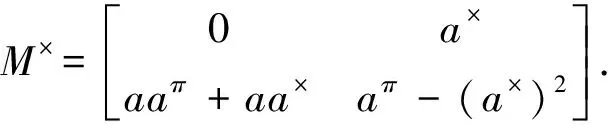
(19)

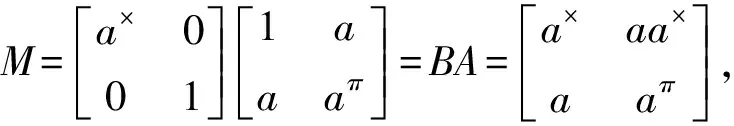
那么BNπA=0∈J(M2(A)).根据引理 2,我们有

□

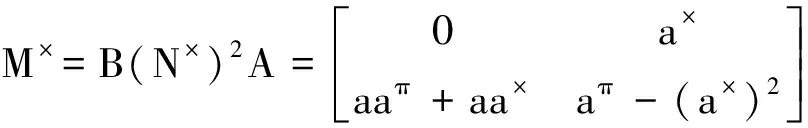
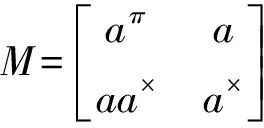
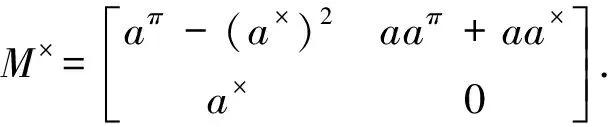
(20)

证明同推论 1的证明相似.

□