高速线材穿水冷却过程的传热分析及数值模拟
赵志恒 张云祥 骆艳萍 陈密达 叶传龙 郭继祥
(1.武汉科技大学 钢铁冶金及资源利用省部共建教育部重点实验室,湖北 武汉 430081; 2.中冶南方工程技术有限公司,湖北 武汉 430223; 3.武钢集团 昆明钢铁股份有限公司,云南 安宁 650302)
温度是高速线材生产中的关键因素,其准确与否与产品组织性能密切相关。线材在穿水冷却过程中的断面温度场,通过传热控制方程和一系列与坯料规格、材料热物性参数和外界冷却条件有关的边界换热模型组成的方程组进行求解,其中温度场的计算方式和水冷强迫对流换热模型的确定是水冷温控预测模型的核心[1]。
为了节省在线计算时间,生产中常采用有限差分方法(finite difference method, FDM)建立温度预报模型。马艳艳[2]、王跃平[3]、陈忠轩[4]等在网格离散化后通过消除假想节点的方法求解得出表面节点温度,用此方法计算换热效率较低的空冷过程温度变化时,误差较小,但用于计算换热效率较高的水冷过程中的温度变化时,误差大、精度较低。由于线材在水冷管中冷却过程为水绕过潜体强制对流换热,所以在求解水冷换热系数时,水冷管内冷却水流速是必须考虑的关键因素之一。Khalifa等[5]、周民等[6]、李辉等[7]在求解换热系数时均采用水流量与冷却管水流通面积之比来计算水流速,并未考虑到线材运输速度和水压对冷却水流速的影响,这会扩大理论水流速和实际水流速之间的误差,从而影响水冷换热模型的精度。
本文在前人研究的基础上提出了一种新的网格离散化划分方式,并通过傅里叶热传导方程推导具有表面温度节点的有限差分模型。在求解水冷换热系数时采用了具有明确物理意义的Mcadame关系式[8],并利用Fluent软件模拟水冷管内真实的水流速度场,构建了高精度的水冷换热理论模型,并在此基础上分析了精轧前预冷段水冷参数对线材表面温降和心表温差的影响。
1 有限差分模型推导
1.1 传热控制方程
根据棒线材椭圆- 圆的孔型变形特点和传热方程,轧件断面用等效圆截面来计算,断面温度场采用一维圆柱坐标下非稳态热传导的傅里叶方程[9- 12]:
(1)
式中:λ为线材导热系数,W/(m·K);ρ为线材密度,kg/m3;Cp为线材质量定压热容,J/(kg·K);T为轧件温度,℃;t为出加热炉后轧件运行时间,s;r为沿线材半径方向的长度,m;qv为轧制变形热或相变潜热,J/mol。
初始条件[13]:
t=0, 0≤r≤R,T(r)=Tin(r)
(2)
边界条件:
(3)
式中:hcom为综合换热系数,W/(m2·℃);Ts为线材表面温度,℃;Tg为环境温度,℃;T(r)为计算的断面温度,℃;Tin(r)为线材各换热过程中的入口断面温度,℃。
1.2 具有表面温度节点的有限差分解推导
水冷段线材截面都为圆形,因此可以使用有限差分方法计算线材的截面温度。其原理为:将线材横截面沿半径方向等分m份,共有m个单元,内部单元的中心为i节点,表面单元的中心为m节点,由于表层单元的节点m距离线材表面还存在Δr/2的长度,且表层单元在与环境进行热交换时温度梯度变化很大,不能直接将其作为线材表面温度,因此在线材表层m单元的上边缘取节点s,该节点能反映线材表面温度真实的非稳态变化情况。中心节点0的选取也是如此,即中心节点0和单元节点1都属于1单元,但中心节点0更能代表心部温度。单元和节点划分如图1所示。

图1 一维有限差分离散单元和节点划分Fig.1 Element discretization and node division in one dimensional FDM
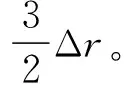
(4)
对于内部单元节点(i≥2),从i-1流入i的热量与从i+1流入i的热量之和使节点i的内能增加,整理显示差分方程得内部节点i温度:

(5)
设边界条件是第三边界条件,既有对流又有辐射,则环境传递给表面的热流为:
(6)
而表面传递给m单元的热流为:
(7)
由于表面没有厚度无法储存热量,所以由式(6)和式(7)求得表面节点s温度:
(8)
对于表层单元m节点,从单元m-1流入单元m的热量和环境传递给单元m的热流之和使得单元m节点的内能增加,整理显示差分方程得表层单元m节点的温度:
(9)
1.3 有限差分解收敛条件

2 水冷换热模型
2.1 水冷管内冷却水流速场的模拟
在影响水冷换热系数的诸多因素中,水冷管内冷却水流速对换热系数的影响最大。传统的水流速计算方法都是通过水量与水冷管内流通面积来计算平均水流速,由于水冷管内线材的穿水速度很大,会加速水流动,得到的水流速偏低并不符合实际情况[14]。本文根据水冷管的实际尺寸,利用Fluent软件模拟计算水冷管内冷却水的流速场,计算条件为:水冷管长度470 mm,水冷管内径30 mm,线材直径19.2 mm,线材速度16.242 m/s,入口压强为0.65 MPa,水量220 m3/h;入口边界条件设为速度入口,入口水管直径40 mm;出口边界条件设为压力出口,出口压强0.1 MPa,其他边界条件都默认为无滑移壁面。流体介质为液态水,密度ρ为97 kg/m3,运动黏度μ为0.905 5×10-6m2/s,黏滞模式选用k-ε模型。选用SIMPLEC算法进行求解,模拟计算的水冷管内冷却水流速场如图2所示。
图3为水量为220 m3/h时水冷管内不同位置水流速的流向矢量图。规定线材移动方向为正,分别在线材表面、水冷管壁和两者之间的3等分点处取得4个不同的水流速。结合图2可知,冷却水在喷嘴口时流速最快,冷却水进入水冷管后部分顺着线材移动的方向从水箱出口流出,部分回流至水箱入口流出,此时水流速趋于稳定。

图2 水冷管内冷却水的流速矢量场Fig.2 Velocity vector fields of cooling water in water cooling pipe

图3 水冷管内不同位置的水流速矢量图Fig.3 Velocity vector diagram of water at different positions in water cooling pipe
由于无法直接测量水冷管内水流速,根据模拟得出的水冷管内不同位置的水流速,将整个水冷管内同一位置的不同水流速绝对值进行均匀化,然后再对水冷管内不同位置的水流速进行均值处理,得到水量为220 m3/h时水冷管水流速平均为18.3 m/s,不考虑线材速度影响的理论水流速为13.3 m/s。同理得出其他水流量与水流速之间的对应关系如图4(a)所示。模拟水压对水流速的影响时,入口边界条件设为压力入口,其他条件相同,得到水压与水流速之间的对应关系如图4(b)所示。通过对水流速的回归分析得到水流量、水压与水流速之间的关系为:
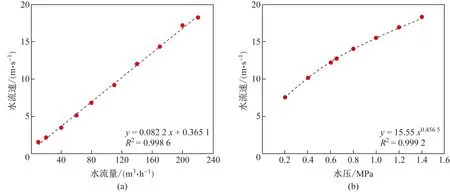
图4 水流量(a)和水压(b)对水流速的影响Fig.4 Influence of water flow rate (a) and water pressure (b) on water flow velocity
vw=(0.365 1+0.082 2Fw)1.223Pw0.456 5
(10)
式中:vw为冷却水流速,m/s;Fw为水流量,m3/h;Pw为水压,MPa。
2.2 轧件表面温度对水冷换热的影响
图5(a)为工业生产收集的轧制φ8~12 mm的HRB400E盘螺时,1、2号水箱的水流量与温降(预精轧后实测温度与精轧前实测温度的差值)之间的关系,1~7号水箱的开冷温度与温降(各水冷段前后实测温差)之间的关系如图5(b~d)所示。图5(a)表明水流量越大,平均温降就越大;图5(b~d)表明开冷温度越高,则水冷段的温降越大,亦即水冷段的换热系数越大。

图5 1、2号水箱的水流量(a)和1~7号水箱的开冷温度(b~d)与温降之间的关系Fig.5 Variation of water flow rate of water tanks No.1 and 2(a) and start cooling temperature of water tanks No.1 to 7(b to d) with temperature drop
2.3 水冷换热模型的构建
在Mcadame计算公式的基础上综合考虑了水冷管内水流速、水温、进入水箱时的线材表面温度(开冷温度)等参数对换热系数的影响[15],构建水冷换热理论模型:
(1-0.007 5Tw)(1-10mTs)
(11)
式中:λw为水的导热系数,W/(m·℃);Tw为冷却水温度,℃;vw为冷却水流速,m/s;Dh为冷却管的水力直径,m;D为线材直径,m;v为流体的运动黏度,m2/s;a为水导温系数,m2/s;C、n、m为模型参数。
结合高速线材工业生产的实测温度, 对水冷换热模型的参数进行了优化[16],结果如表1所示。

表1 优化的水冷换热模型参数Table 1 Optimized parameters of water cooling heat transfer model
2.4 模型验证
实测换热系数的迭代计算法:根据预精轧出口实测温度,设定1、2号水箱的水流量、水压和喷嘴开关等参数,先由水流量给定一个理论换热系数初始值,然后用第1章中的有限差分法计算经过1、2号水冷箱冷却后线材精轧前温度,再与精轧前实测温度比较得出计算值偏差。当偏差大于1 ℃时,返回预精轧出口处,增大或减小换热系数的自学习系数,并重新计算得到精轧前温度,再与精轧前实测温度比较得出计算值偏差,直至偏差小于1 ℃结束计算,得到1、2号水箱的实测换热系数为理论换热系数初始值与自学习系数的乘积。表2为通过迭代法计算得到的换热系数实测值和式(11)计算值。由表2可知,预报计算的换热系数与实测换热系数吻合较好。
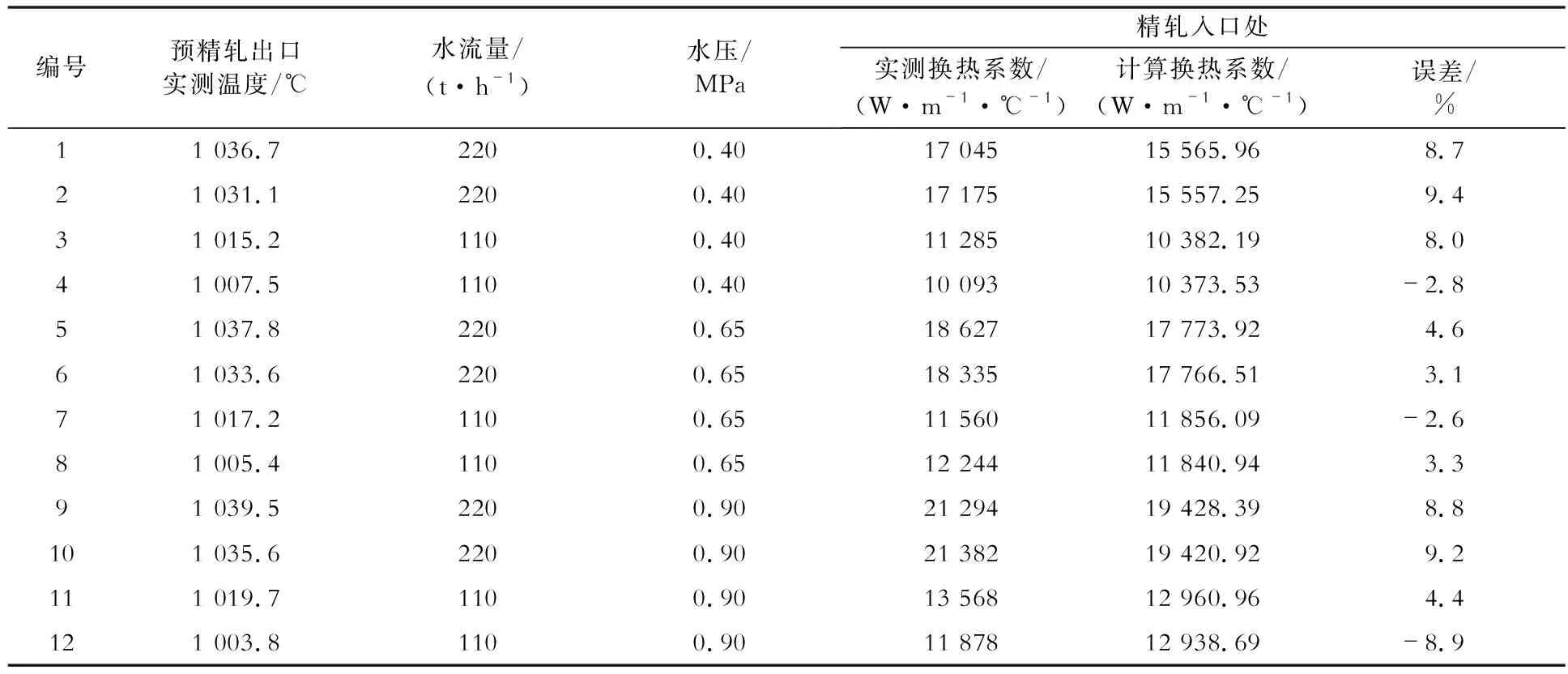
表2 换热系数实测值与计算值的比较Table 2 Comparison between measured and calculated values of heat transfer coefficients
3 水冷参数对冷却效率的影响
采用高速线材轧制φ8~12 mm的HRB400E盘螺时,为了克服精轧机组急剧轧制温升并获得成品细晶粒组织,需进行控温轧制。预水冷段目的是将线材出预精轧机组后的温度1 000 ~1 040 ℃降低至精轧前的800 ℃左右,该段水冷过程能够确保后续线材出吐丝机温度也在800 ℃左右,避免在散卷风冷线上产生粗大先共析铁素体组织。预水冷段水箱布置如图6所示。
根据图6线材预水冷段的冷却过程将换热边界条件分成两类:一类为区域Ⅰ、Ⅲ、Ⅴ中线材通过与环境辐射和与空气的自然对流,综合换热系数采用马靳江等[17]所用公式进行计算;另一类为区域Ⅱ、Ⅳ中线材与冷却水的强迫对流,综合换热系数采用式(11)进行计算。

图6 预水冷段水冷箱布置Fig.6 Layout of water cooling tanks in pre- cooling section
水冷箱内部水冷喷嘴排布如图7所示,共有13个喷嘴,按顺序分别为1个顺向干燥喷嘴、9个冷却喷嘴、2个逆向清扫喷嘴和1个逆向干燥喷嘴,其中干燥喷嘴和清扫喷嘴在水箱运作时处于常开状态,其余9个冷却喷嘴3个为一组,由3个气动蝶阀控制。在下文分析中,水箱的开关情况用(1,1,0,1)表示,前3个数字代表控制9个冷却喷嘴的3个气动蝶阀的开关情况,第4个数字代表控制2个清扫喷嘴的气动蝶阀的开关情况,其中1代表开关开启,0代表开关关闭。

图7 水冷箱内部结构图Fig.7 Internal structure of water cooling tank
结合差分模型和换热模型,利用C#代码在Visual Studio中开发了棒线材热连轧温度场模拟预报系统,并用该预报系统模拟计算线材在预水冷段的温度场变化。在实际生产中,线材经预精轧机组到进入第1个水箱时,由于轧制后没有足够的时间进行温度回复,在进入水冷箱时线材心表已有一定的温差,因此为了使模拟结果更好地符合实际,计算时应考虑该现象。利用有限差分法模拟计算温度场时,将线材截面沿半径方向划分为20等份,心部温度取节点0处的温度T0,表层温度取单元节点m处的温度Tm,表面温度取节点s处的温度Ts。
3.1 水流量对冷却效率的影响
图8为1、2号水箱的水流量均为110 m3/h时线材断面各节点温度变化。从图8水冷段可知,在与空气接触进行换热的区域,由于热交换的效率不高,线材表面和表层单元节点之间的温差很小。进入水冷箱后,线材表面与冷却水接触进行强迫对流换热,使得表面温度骤降,而表层单元节点由于离线材表面有一定距离(Δr/2),温降没有表面剧烈,从而使得表层单元节点和表面之间产生温差。而在离开水冷箱的一瞬间,线材表面重新与空气接触发生热辐射,由于水冷而增大的心表温差使得表面温度急剧回升,并使其再次接近表层单元节点温度。由图8可以看出,在2号水箱出口处,线材表面与表层单元节点之间的温差达到最大,最高可达57.18 ℃。因此在实际生产中,掌握线材穿水冷却过程中表面瞬时温度的变化可以有效避免因过冷而产生马氏体环。

图8 水流量为110 m3/h时线材断面各节点温度随时间的变化Fig.8 Variation of temperature of each node on the cross- section of wire with time under the condition of water flow of 110 m3/h
水流量对水冷换热系数有直接影响。表3为线材经不同水流量预水冷后,在精轧机组前测温点处的表面温降和心表温差。由表3可知,水流量越大,线材表面温降越大,在220 m3/h的水流量下精轧机组前测温点的表面温降达225.7 ℃,心表温差超过了200 ℃。

表3 不同水流量下线材表面温降和心表温差Table 3 Surface temperature drop and core- surface temperature difference of wire under the condition of different water flows
3.2 喷水次序对冷却效率的影响
图9是开启不同水箱开关时线材心部、表面以及平均温度的变化。当仅开启1号水箱,即开关为(1,1,0,1)、(0,0,0,0)时,线材经过水冷后进入精轧机组时的心部温度为1 047.1 ℃,表面温度为955.9 ℃,心表温差为91.1 ℃;而当仅开启2号水箱,即开关为(0,0,0,0)、(0,1,1,1)时,线材进入精轧机组时的心部温度为1 061.2 ℃,表面温度为953.5 ℃,心表温差为107.7 ℃。在所有参数都没有变化的前提下,仅改变水箱开关的开启方式,就能使线材经过水冷后的心表温差减小16.6 ℃。由此可知,在实际生产中,在选择水箱开关和喷嘴开关的开启次序时,多个水箱应优先开启前面的水箱,同一水箱中应优先开启前面的冷却喷嘴,线材越早结束水冷,回复时间就越长,心表温差就越小。

图9 不同喷水次序条件下线材断面温度随时间的变化Fig.9 Variation of temperature on the cross- section of wire with time under the condition of different water spray sequences
3.3 开冷温度对冷却效率的影响
开冷温度为1 015、1 030和1 040 ℃时线材经过预冷却系统后,在精轧前测温点处的表面温降及心表温差如表4所示。可知线材在不同开冷温度下进入水冷箱与冷却水进行热交换时,开冷温度越高,线材在水冷箱中的换热效率就越高,开冷温度相差25 ℃时表面温降仅相差5.3 ℃。图10为线材出预精轧机组最后一架轧机的温度分别为1 040和1 015 ℃时的断面温度变化曲线。由图10可以看出,开冷温度为1 040 ℃的线材进入水箱后的温降几乎与开冷温度为1 015 ℃时的相同;在回复段由于心表温差较大,表面温度回复速度较快,在到达精轧机组第一架轧机时,两种不同开冷温度的线材的心表温差仅相差5.1 ℃。

表4 不同开冷温度下线材表面温降和心表温差Table 4 Surface temperature drop and core- surface temperature difference of wire under the condition of different start cooling temperatures

图10 不同开冷温度下线材断面温度随时间的变化Fig.10 Variation of temperature on the cross- section of wire with time under the condition of different start cooling temperatures
3.4 线材穿水速度对冷却效率的影响
线材穿水速度分别为8、16和30 m/s时线材心部和表面温度的变化如图11所示。由图11可知,线材在辊道上运输速度越小,在水冷箱中的温降就越大,但经过回复段回复后的心表温差越小。当线材穿水速度为8 m/s时,线材经过预冷段后的表面温降高达314.6 ℃,但经过回复段后在进入精轧机组第一架轧机时的心表温差只有78.5 ℃;而当线材穿水速度为30 m/s时,线材表面温降仅为170.3 ℃,进入精轧机组时心表温差却有215.7 ℃。这是由于线材穿水速度越小,在水冷箱中停留的时间越长,线材与冷却水热交换的时间增加,温降也越大;同样在回复段,由于线材心表之间有更多的时间进行热量传递,心表温差大幅度减小。反之,大的线材穿水速度的结果则相反。
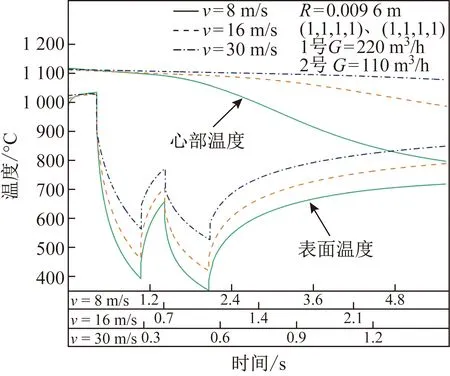
图11 不同穿水速度下线材断面温度随时间的变化Fig.11 Variation of temperature over the cross- section of wire with time under the condition of different water-through speeds
4 结论
(1)提出了一种新的网格离散化划分方式,在表层单元的上表面增加一个表面节点,该节点理论上可精确反映线材表面温度的非稳态变化;在此基础上推导出具有该表面温度节点的有限差分解模型,应用该差分模型计算线材在预水冷段1、2号水箱水量为220~220 m3/h时的温度场变化,表层单元节点与表面节点之间的温差达64.96 ℃。
(2)利用Fluent软件模拟得出水冷管内冷却水的流速场,并回归分析得出水流量、水压与水流速之间的关系;综合考虑了水温、轧件开冷温度对换热系数的影响,构建了高速线材穿水冷却过程的非线性换热模型,并用实测值验证了模型的精度,误差在±10%之内。
(3)结合差分模型和水冷换热模型,研究了预冷段水冷参数对表面温降及心表温差的影响,得出水流量对表面温降和心表温差的影响较大。水流量越大,表面温降和心表温差越大;多个水箱应优先开启前面的水箱,同一水箱中应优先开启前面的冷却喷嘴,可以在不改变工艺参数的条件下降低轧件的心表温差;轧件开冷温度对表面温降和心表温差的影响较小;降低线材穿水速度可以增大表面温降和降低心表温差。

