基于神经网络模型的致密气藏分段压裂井产能预测

王丹群， 李治平*， 毛得雷

(1.中国地质大学(北京)能源学院， 北京 100083； 2.中联煤层气国家工程研究中心有限责任公司， 北京 100095)

水平井分段压裂技术的广泛应用使得致密气藏快速地进入了工业化开采阶段，对于压裂后产能预测的难点主要来源于两方面：一是由于压裂后产能的影响因素众多，如包括流体性质以及储层岩石性质的地质因素、包括完井方式或工作制度等开发因素、压裂后裂缝的渗透率、裂缝长度等裂缝因素以及压裂过程中的人为因素，都让预测的无阻流量和影响因素之前呈现出复杂的非线性关系。二是由于压裂产能预测的模型传统方法大多为解析解法、半解析解法和数值解法，由于所探讨模型多做大量理想化假设，导致预测产能的结果误差很大。

早在1988年，Joshi[1]率先提出了水平井产能公式的计算方法，也成为后续研究学者产能模型演变的基础公式。中国研究学者郎兆新等[2]在综合Joshi[1]和Mukherjee等[3]的研究的基础之上提出了基于严格高等渗流理论求解出水平井压裂的产能公式。随后宁正福等[4]、韩树刚等[5]、位云生等[6]、黄亮等[7]、杨兆中等[8]研究学者都对致密气藏水平井分段压裂井产能的模型进行了推导和修正，但应用方法并不仅仅局限于一种，多利用位势理论和叠加原理。基于郎兆新等[2]的物理模型假设思想，宁正福等[4]对压裂水平井的产能预测公式进行了重新修正，在产能公式的求解和推导过程中应用了位势理论、叠加原理和矩阵方程数值分析求解方法。韩树刚等[5]的研究基于动量定理和流体力学理论，将水平井产能公式当中压力等值运用真实气体状态方程和压力函数替代为气体表示，建立气藏压裂后水平井地层渗流特征和水平井筒管流耦合的产能计算模型。位云生等[6]建立以单压裂段为单元的物理模型，运用单压裂段压降叠加分析方法和单压裂段产量递减分析方法，并且将气藏渗流和变流量井筒流动联系起来，建立了多段压裂水平井从地层到井底全过程流动的产能预测方程组是位等人所提出的创新点。2017年黄亮等[7]提出的模型分别对地层段、裂缝段、射孔孔眼段和井筒段的压降进行耦合，建立了考虑气体从地层渗流至水平井筒内全过程压降分析的低渗致密气藏压裂水平井产能预测新模型，并且考虑到了人工裂缝的应力敏感性，给裂缝渗透率增加了裂缝渗透率敏感系数，增加产能模型的准确性。

近年来对于致密气藏压裂水平井的产能模型的探究并未停止，2019年杨兆中等[8]对致密气藏水平井分段压裂后产能的计算模型进行了更创新的分析方法，建立利用高渗透带代表水平井分段多簇压裂后的裂缝的物理模型，根据等效渗流理论、位势理论、叠加原理，对高渗透带进行微元计算，建立致密气藏分段压裂水平井非稳态产能计算模型，并利用数值模拟分析高渗透带以及裂缝特征对压裂后水平井产能的影响，实例验证模型准确性高。但对于利用数学方法建立模型而言，理想化的假设、模型求解过程当中简化的计算方法，这些都导致产能模型最后的计算结果误差较大。

近年来，神经网络方法作为最具有预测性的一种模型广泛应用于油气田领域。利用神经网络模型等机器学习的方法可以将复杂的地质施工工程和人工操作因素作为变量类型，不考虑实际的地质构造和物理模型过程，让产能计算更加方便。将机器学习方法融合进气井产能预测取得了显著的成果，如许敏等[9]、叶双江等[10]、王黎等[11]、庄华等[12]；当然，神经网络不仅应用于产能预测，杨志浩等[13]、于聪灵等[14]、李鑫羽等[15]利用神经网络进行地质勘探方面或压裂选段的预测为油气田领域的发展注入崭新力量。其中，Sheikhoushaghi[16]、Zhou[17]、Li等[18]都利用了神经网络模型对不同地区不同油气藏的产能或油气藏性能进行了预测。Zhou等[17]基于贝叶斯神经网络对致密气砂岩渗透率进行预测，但模型中仅选取岩心孔隙度、常规测井因素作为输入项，主要数据输入项选取较少且没有比较；Sheikhoushaghi等[16]比较了几种神经网络模型的性能，最后选取了粗糙神经网络模型进行伊朗油田产量预测，模型准确率良好；Li等[18]利用基于时间序列的神经网络模型进行煤层气产量的预测；Peng等[19]利用深度卷积生成对抗网络(deep convolution generation adversarial network，DCGAN)进行裂缝网络形态的模拟从而预测致密油气多级压裂水平井储层的压力分布。

但目前对于上述研究内容存在两方面不足：一是在进行神经网络模型选择输入层节点因素时，选用产能模型多为二项式等简单产能模型，考虑因素有限导致模型准确率降低；二是模型考虑多为直井、水平井，对于压裂水平井工程因素，例如裂缝数、裂缝渗透率等考虑不足，对于致密气压裂水平井的神经网络模型产能预测研究较为匮乏。现基于致密气藏分段压裂水平井的产能模型选取影响因素，根据灰色关联可视化方法的不同取值选取不同主要因素作为网络模型的输入层节点，建立神经网络模型，对模型进行训练使其可以预测待压裂井产能。

1 致密气藏分段压裂水平井影响因素

Joshi等[1]提出简化三维渗流模型为二维渗流模型的想法，基于此思想，探究水平井产能模型的研究学者多利用上述简化思想进行产能物理模型的假设和建立。杨兆中等[8]考虑利用复杂渗透缝网来表示在射孔段部分周围引起的复杂裂缝形态(如图1所示)。

图1 压裂水平井物理模型示意图Fig.1 Schematic diagram of physical model of fractured horizontal well

双重介质模型所涉及的两个渗流过程，做如下的等效，分别为：所形成的高渗透带当中基质流向水平井筒和高渗透带中缝网流向水平井筒两个过程。借鉴杨兆中等[8]模型，整合影响致密气藏分段压裂水平井产能因素，如表1所示。

表1 分段多簇压裂水平井产能影响因素Table 1 Factors affecting productivity of multi-cluster fractured horizontal wells

2 灰色关联可视化分析法

灰色关联多因素分析方法主要应用于求解寻找各个因素之间的主要联系关系，输入各个因素序列的样本数据，根据计算过程计算灰色关联度描述因素序列之间关系的紧密强度以及次序。灰色关联度数值越大求取样本数据数值序列与输出主序列关联性越大；反之则越小。

2.1 主系列与相关因素系列的确定

(1)主系列。

X1=[x1(1),x1(2),…,x1(n)]

(1)

(2)相关因素的确定。

X2=[x2(1),x2(1),…,x2(n)]

(2)

X3=[x3(1),x3(2),…,x3(n)]

(3)

⋮

Xs=[xs(1),xs(2),…,xs(n)]

(4)

⋮

Xm=[xm(1),xm(2),…,xm(n)]

(5)

2.2 计算各序列的初像值

(1)初像值。

s=0,1,…,m

(6)

(2)计算序列的绝对数值。

Δs(k)=|x′1(k)-x′s(k)|

(7)

Δs=[Δs(1),Δs(2),…,Δs(n)]，

s=1,2,…,m

(8)

(3)最大值M和最小值m的计算。

M=maxsmaxkΔs(k)

(9)

m=minsminkΔs(k)

(10)

2.3 计算相关系数

(11)

2.4 灰色关联度的计算

(12)

通过Python编程实现灰色关联法结果可视化，如图2所示，可视化图形每一块为计算灰色关联值，与每一项元素一一对应，每一列代表选择序列。

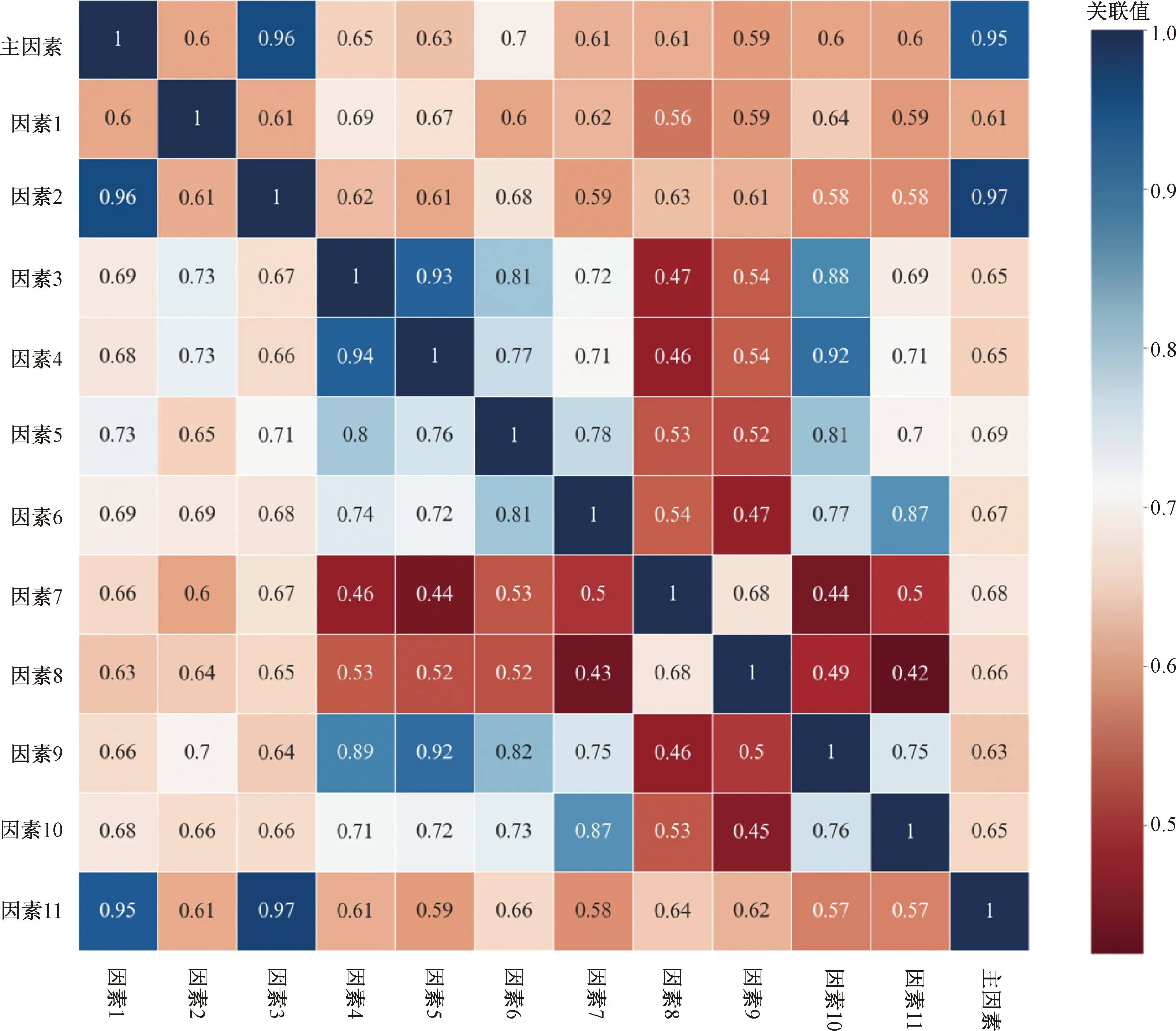
图2 灰色关联可视化分析举例Fig.2 Example of grey correlation visual analysis

通过选取不同灰色关联值因素，选取所需要的神经网络模型输入层。数据分析方法众多，灰色关联分析法的主要优势是：一是对于样本数据数量和分布都没有具体强制性的规定；二是计算的过程更为简洁轻便，类似于定性分析。灰色关联分析法的优势适合于致密气藏压裂水平井产能影响因素的主要影响因素的确定，影响因素的数量众多，样本繁杂，影响因素之间呈现复杂的非线性关系，利用灰色关联分析法不需要对样本数据进行要求和处理，可以更加简便地计算出主要影响因素。

3 BP神经网络模型设计

神经元之间的交互连接组成人工神经网络的基本机构，典型的基本神经元网络结构示意图如图3所示。其中结构中各个部分各司其职，输入层主要负责接收外界传递来的信息；输出层作为输出系统处理后结构的输出部分；隐含层位置位于输入层和输出层之间，作用也最为重要，主要负责处理输入层传递进来的外界信息。

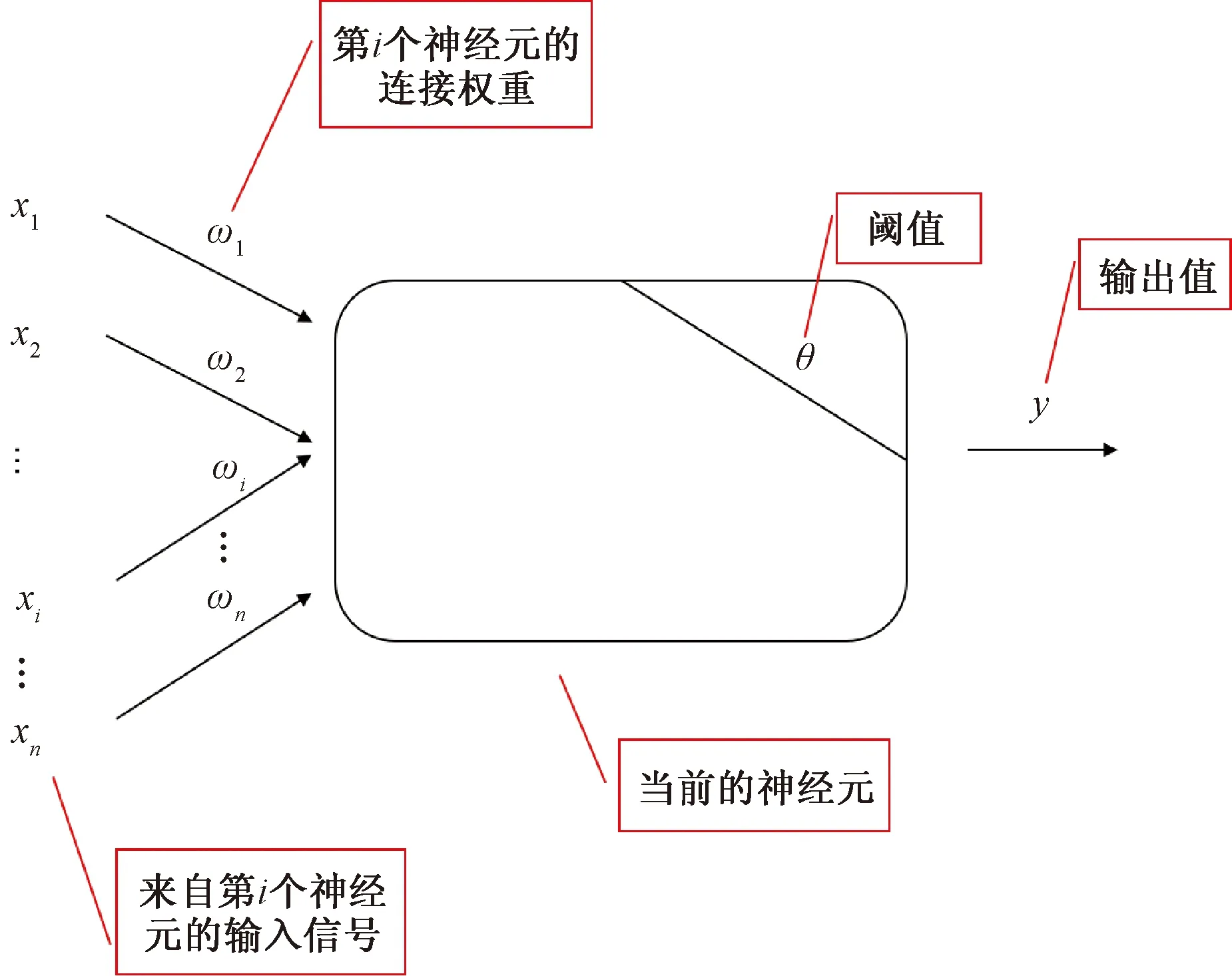
图3 典型神经元模型示意图Fig.3 Schematic diagram of typical neuron model

拟用经典重要的前向网络模型当中的反向传播(back propagation，BP)神经网络模型进行建立产能预测模型。BP神经网络模型的两个重要原理为正向数据传输和误差反馈矫正，如图4所示。

在图4的正向转播过程中，其他神经元传递到本神经元的信息输入量进入神经元结构从输入量部分，通过连接权值以及神经元阈值的加和计算，输出得到计算量，传递给隐藏层当中；隐藏层的神经元经历重复的上述计算得到的变量传递给下一层——输出层；至此前向传递阶段大部分完成。接收到传递信号的输入层会把期望输出值与计算传递的输出值进行比较，计算出误差后将得到误差反向传递给输入层，进行输出层的权值和阈值的不断调整，再次进行循环计算。在循环计算的过程之中，计算误差值小于模型建立设定的期望误差后，循环计算结束输出结果，以上就是误差反转矫正的过程。

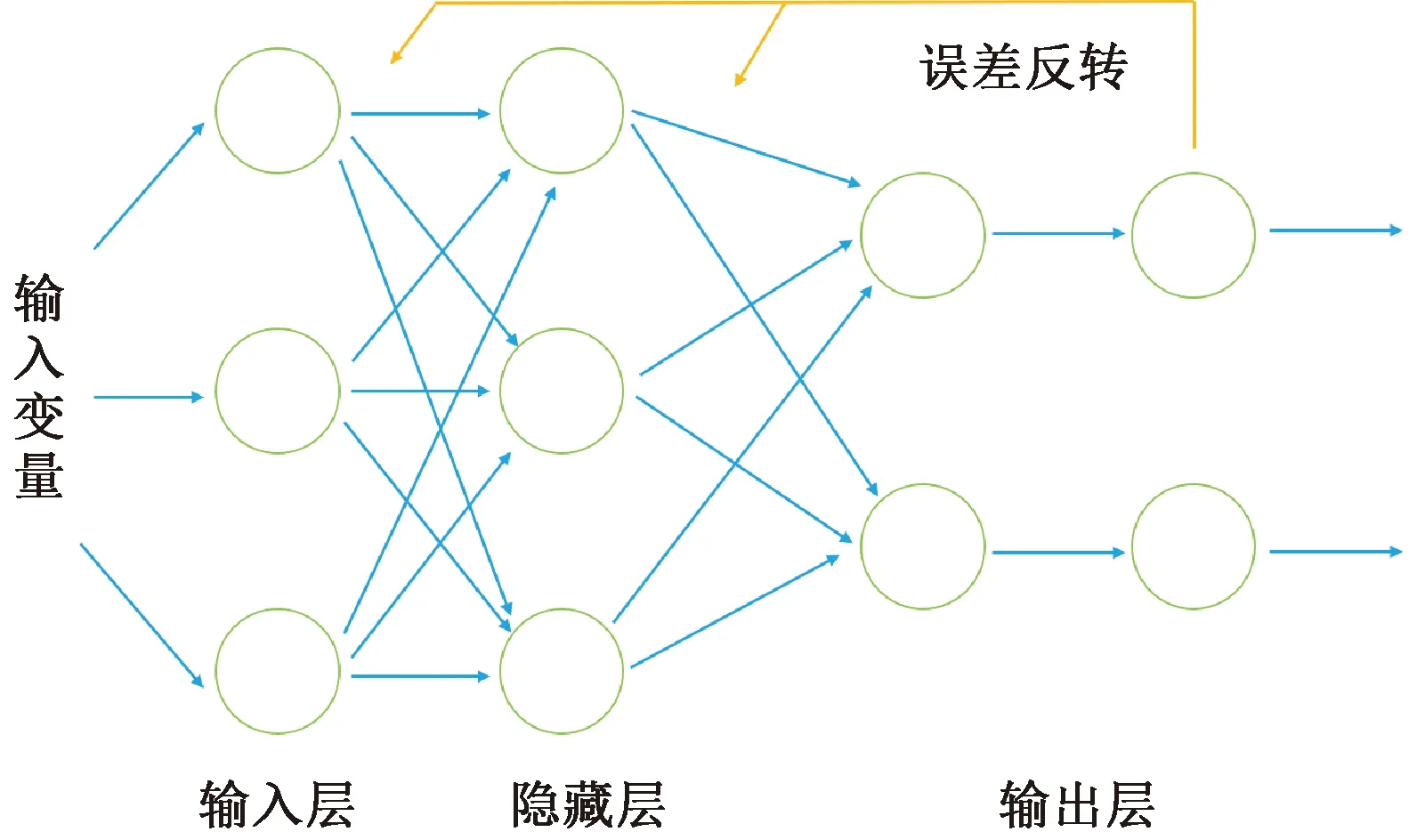
图4 BP神经网络模型网络结构图Fig.4 Network structure diagram of BP neural network model

对于BP神经网络模型的设计，一般从神经网络模型的组成部分的开始，即网络层数、每一层当中的神经元个数、激活函数、学习速率等。本部分就从以上几个方面来进行BP神经网络模型的设计，便于对产能预测模型进行构建。

3.1 网络的层数

对于所建立的致密气藏分段压裂水平井的产能预测模型，建立三层网络结构，即可解决复杂问题又可避免网络复杂化的问题出现。

3.2 隐含层神经元个数

对于设定隐含层神经元的个数，研究学者也进行了探究。一般来说，确定三层神经网络当中隐含层的神经元个数有如下几种经验公式。

(13)

式(13)中：K为输出层节点数；n为输入层的节点数；n1为隐含层的节点数。

n1=p-1

(14)

式(14)中：p为输入层的节点数。

n1=log2n

(15)

(16)

式(16)中：m为输出层节点数；a为1～10的一个常数。

n1=(0.43mn+2.54m+0.77n+0.35+

(17)

输入层节点与隐含层节点数设置直接影响神经网络模型预测值的准确性，为此选择不同隐含层节点设置训练查看误差曲线方法，并与上述计算公式对比确定节点数设置，

3.3 学习效率选取

BP神经网络模型的学习效率的选取一般为0.01～0.8， 神经网络模型系统的不稳定会由于设定了过大的学习速率导致；但小于适合值和正常值的学习速率会导致神经网络模型在计算时收敛速度过慢，计算速率大幅度降低、训练模型的时间增长。

3.4 期望误差的选取

选取合适期望误差值的方法为：同时对其他因素相同而设定的期望误差值不同的神经网络模型进行训练，以此来选取合适的期望误差，产能预测神经网络模型的期望误差值设定为0.001，效果最好。

4 实例分析

4.1 灰色关联分析法筛选主要数据

选15口井数据作为测试组实例，如表2所示，对所有分段压裂水平井影响因素进行灰色关联可视化分析，利用Python语言实现计算结果，如图5所示。

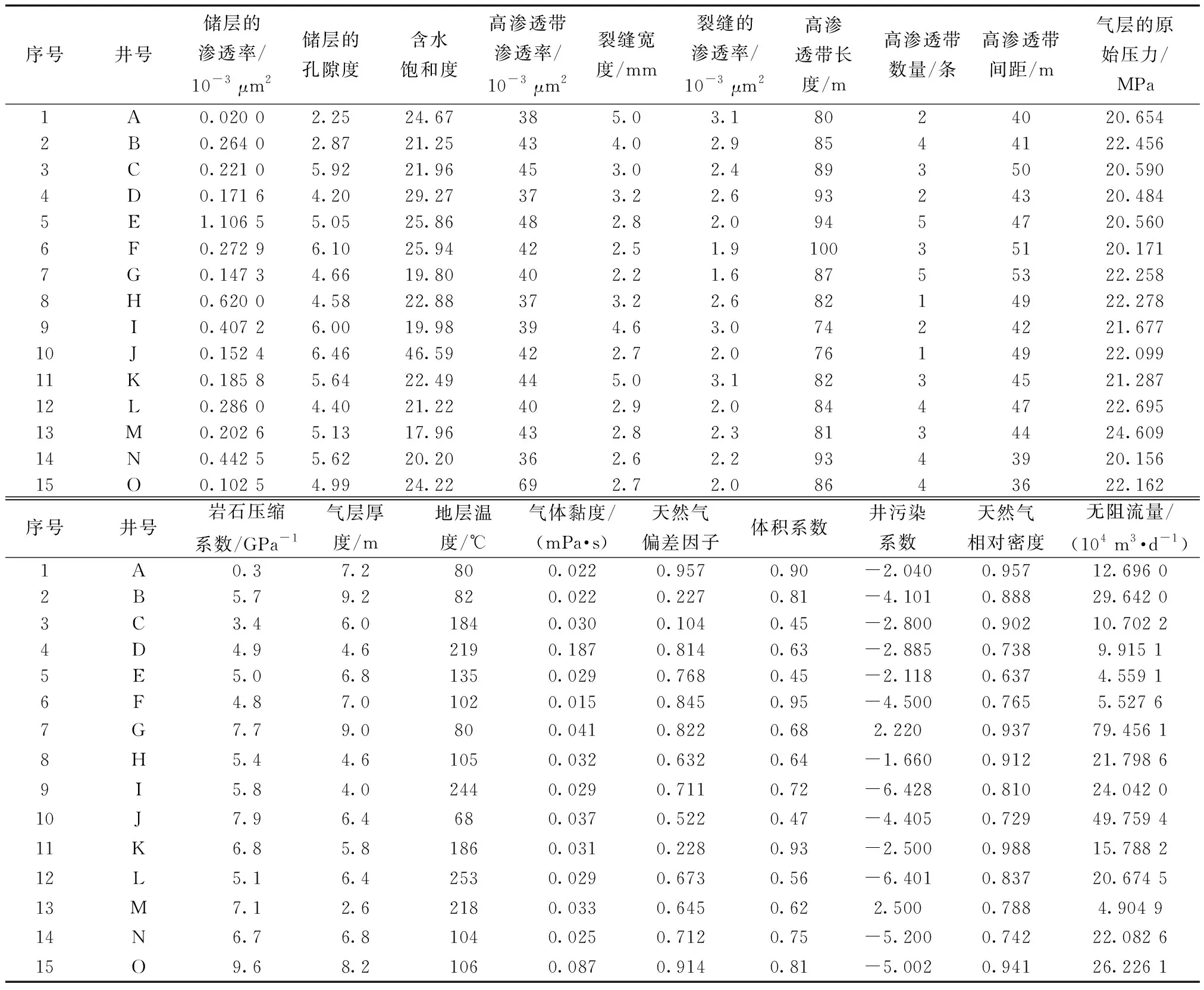
表2 测试组各井参数数据表Table 2 Parameter data of each well in the test group

编写程序并代入实际数据得到灰色关联分析计算结果，如图6所示，方格数据代表影响因素序列(表2中除了“无阻流量”外的18列数据)与主序列(表2无阻流量序列)关联数值得到影响因素关联紧密性。

神经网络模型准确性和运行速度等性能好坏与输入层节点与隐含层节点设置有直接关系，分别以灰色关联数值0.7、0.72、0.74作为选择主要影响因素的标准，对比3种不同输入层节点的神经网络训练精度得到最佳模型配比选择。

4.2 神经网络模型建立并训练

利用Python语言实现神经网络建立，灰色关联数值为0.7时，输入层节点为18个；为0.72时，输入层节点为12个；为0.74时，输入层节点为7个。隐含层节点设置3、6、10个，以对比得到误差最小的训练模型进行预测，模型学习效率0.04，迭代步数设置为5 000步完成模型训练，查看误差曲线确定最佳训练模型，结果如图7～图9所示。其中set0、set1、set2表示隐含层节点为3、6、10的模型。

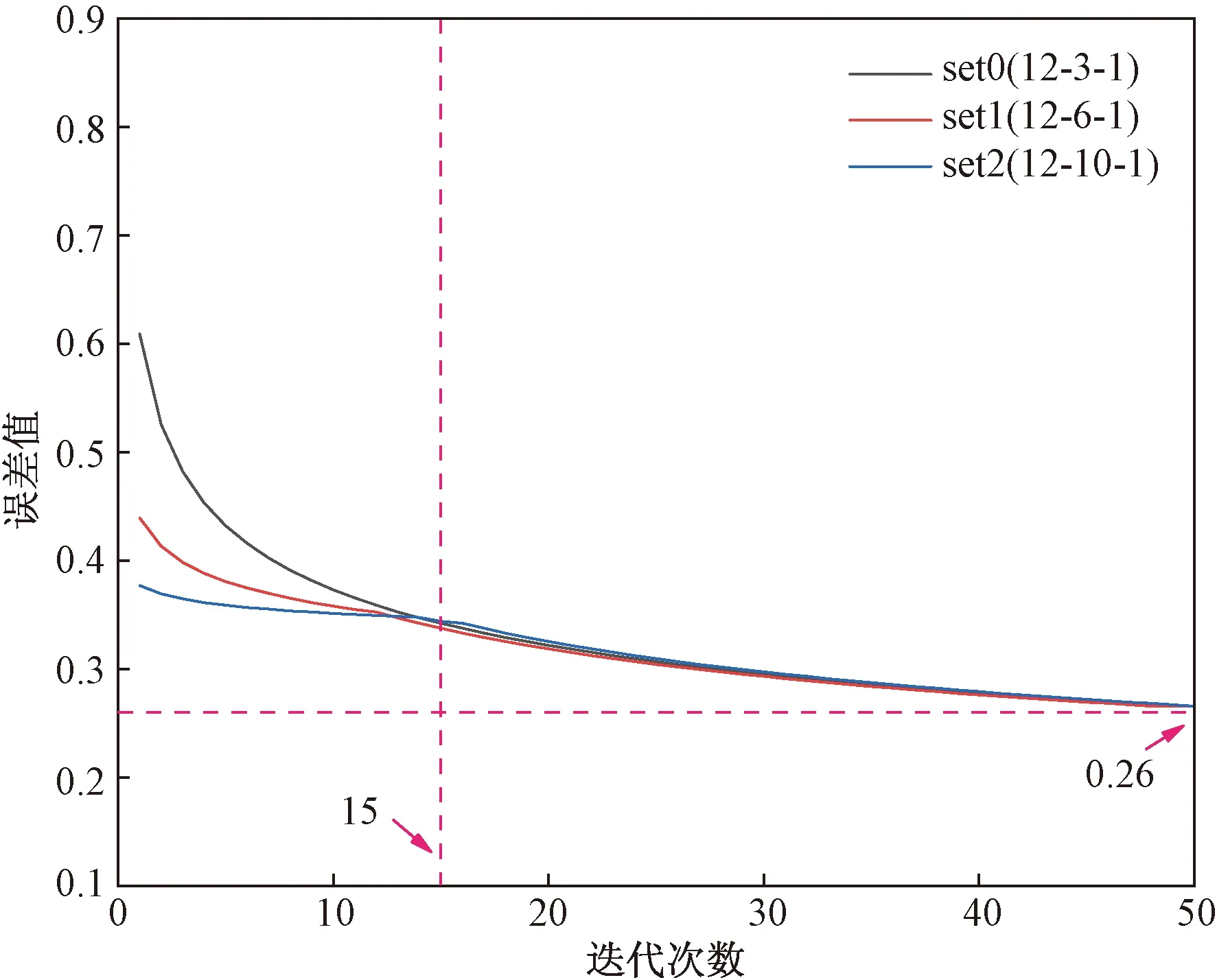
图8 界限值0.72误差曲线图Fig.8 Error curve of limit value 0.72

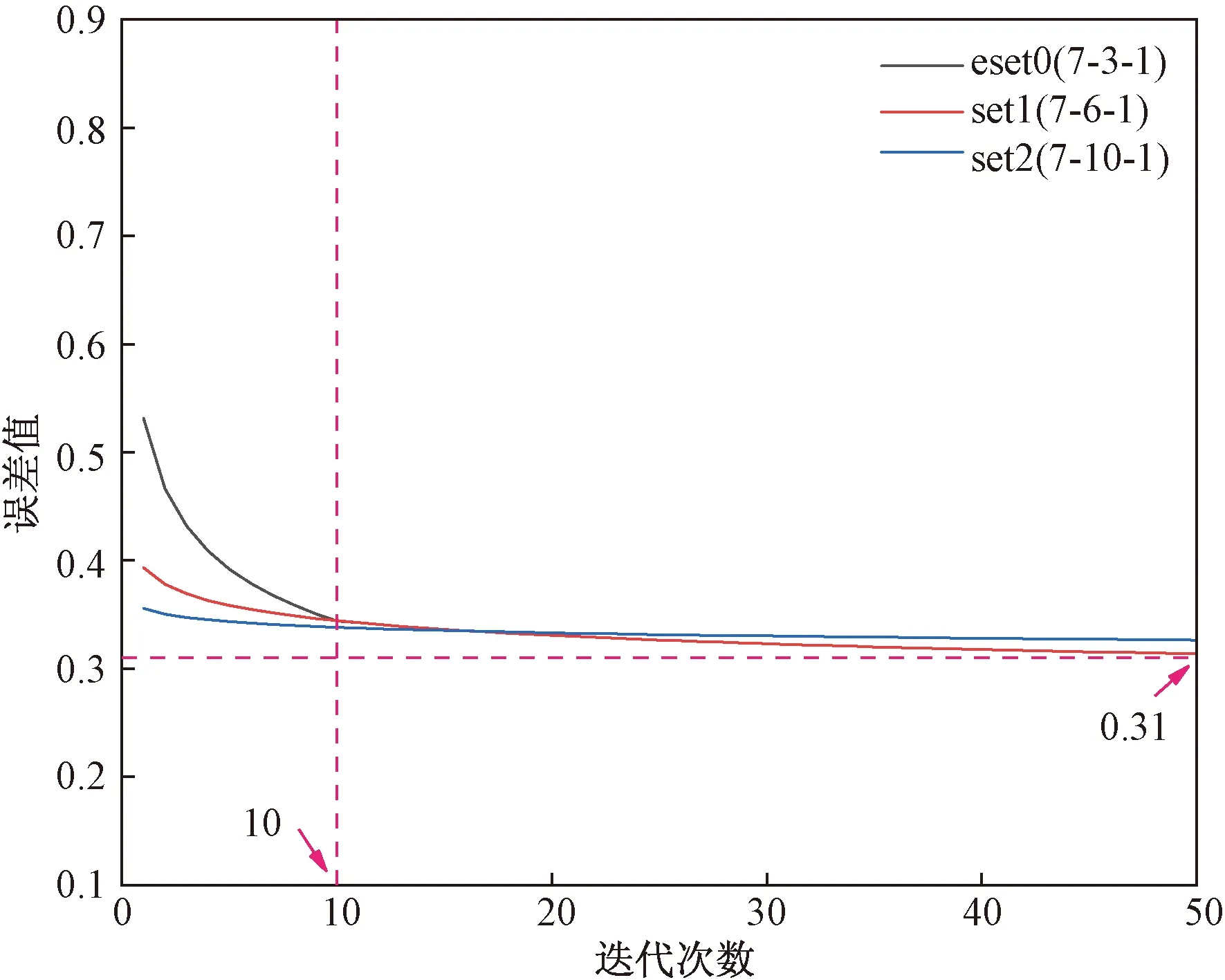
图9 界限值0.74误差曲线图Fig.9 Error curve of limit value 0.74

结果显示，输入层节点越少，误差曲线降落越快，训练模型稳定越快；比较3种输入模型稳定误差值，选取灰色关联值0.72为界限，输入层为12个节点时模型稳定时误差最小。

由图7～图9可知，set1、set2模型误差曲线下降速度最快，故取模型12-7-1、12-8-1、12-9-1再次训练确定最佳训练模型隐含层节点数，结果如图10所示。

图10 隐含层训练模型对比图Fig.10 Comparison of hidden layer training models

隐含层节点设置为7时可以得到误差曲线下降速度快、误差小的训练模型，选用神经网络模型设计隐含层节点公式计算得隐含层节点数为7时也可以印证结果，训练模型选取完成进行待压裂井的实际预测。

4.3 实例压裂井产能预测

选取训练模型输入节点12个、隐含层节点7个、输出层节点1个结构进行实例分段压裂水平井产能预测。选取实际井4口进行压裂预测，待压裂井实际数据如表3所示。输入至训练好的模型进行产能预测，得到预测值以及误差如表4所示。

表3 分段压裂水平井预测组数据Table 3 Prediction group data of staged fracturing horizontal wells

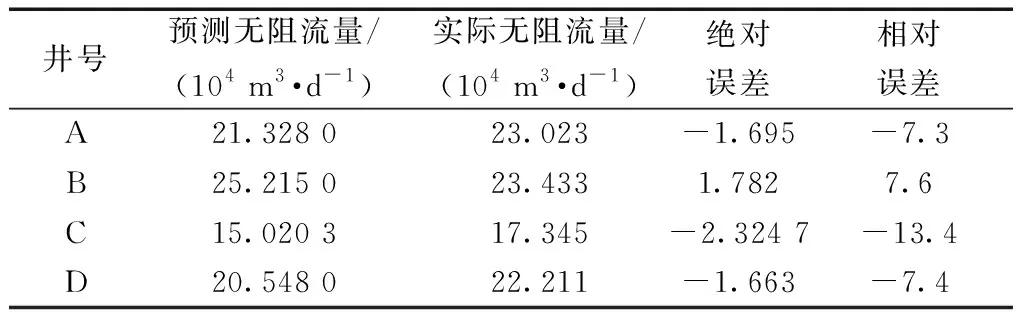
表4 产能预测误差表Table 4 Productivity prediction error

5 结论

(1)对于致密气藏的分段压裂井产能模型采用高渗透带的物理模型进行产能模型的建立更加简便高效。

(2)灰色关联可视化分析法可以帮助我们筛选对产能主要影响因素，通过不同灰色关联值取值确定最佳训练模型的结构为12-7-1，虽然设置输入层个数越少训练速度越快但也会造成训练误差较大。利用实际矿场数据对建立产能模型进行学习和训练，误差效果图显示，模型数据训练良好，模型精确度较高。

(3)利用训练好的神经网络产能预测模型对压裂井产能进行实际预测，预测结果显示预测值与真实值误差较小。神经网络模型可以用来解决致密气藏分段压裂井产能预测问题，对于影响因素与无阻流量之间的复杂非线性问题，神经网络模型显示出良好的性能，可以用于矿场的实际预测，对接下来矿场的实际生产工作制度有一定的理论指导意义。