基于SA-PSO算法优化LS-SVM的基坑土层等效参数反演*
曹净 唐斌懿 李豪
(昆明理工大学建筑工程学院,云南 昆明 650500)
0 引言
岩土参数反算可视为对应目标函数寻求最优解,而岩土本身是复杂的、具有区域性和时空效应的材料,使得在多数情况下的目标函数是复杂非线性的函数,因此当选取不同的方法进行求解时,往往存在方法上的局限性。如模拟退火算法遇到变量多、目标函数复杂时,其求解时间过长,且容易在搜索过程中由于执行概率接受环节而遗失当前遇到的最优解[1]。遗传算法由于是互相共享信息,整个种群的移动是比较均匀地向最优区域移动,而在粒子群算法中,只有局部最优解或全局最优解传递信息给其他粒子,属于单向的信息流动,整个搜索更新过程是跟随当前最优解的过程[2]。一般情况下,粒子群算法的收敛速度更快。本文提出一种基于SA-PSO混合算法构建最小二乘支持向量机土层等效参数反分析模型,建立支护结构位移与土层参数之间的非线性回归关系,利用位移反演得到相关岩土力学参数的方法,为基坑工程后期施工及设计优化提供了一定的参考。
1 岩土力学参数反演原理
基坑施工过程是连续且复杂的,影响基坑变形的因素较多,通过常规方法建立基坑土层参数与支护结构水平位移间的显示表达式是非常困难的。本文利用均匀试验构造出试验样本进行试算,以期得到不同样本所对应的支护结构水平位移值,再通过SA-PSO混合算法对最小二乘支持向量机的正则化参数和核参数进行寻优处理,最后运用最小二乘支持向量机来模拟基坑支护结构水平位移与土层参数间的非线性映射关系,以模拟的支护结构计算水平位移与实测支护结构水平位移之差最小作为目标函数,当目标函数取得极小值时,所得土层参数即为待反演参数最优值。其建立步骤[3-5]如下:
1)通过均匀设计思想和已知基坑支护结构数据共同建立学习样本,并对训练样本和测试样本进行归一化处理。
2)设定最小二乘支持向量机的模型参数即正则化参数 和核参数 的取值范围,并在此范围内随机产生初始种群。
3)确定种群的适应度函数通过式(1),计算每个种群个体的适应度,若满足收敛条件,则将当前输出解更新为全局最优解。

其中:yi+为第i个样本真实值,yi-为第i个样本模拟值,可根据式(2)获得。而LSSVM模型的优化,则是通过SA-PSO混合算法不断迭代求解参数(,),并使其满足适应度函数取得最小值。
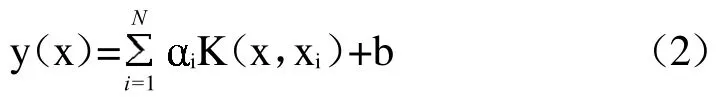
4)若不满足收敛条件,则根据式(3)和式(4)将种群的每个粒子进行位置与速度更新。更新后再返回步骤3。

5)训练结束,利用寻优得到的最优参数建立最小二乘支持向量回归机模型。
6)建立支护结构位移计算值与位移实测值不断逼近的函数关系,即目标函数:
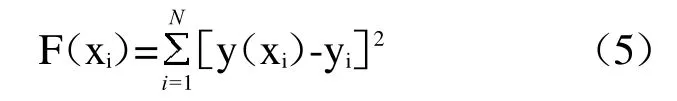
其中y(xi)为位移计算值,yi为位移实测值。
7)求解目标函数,运用SA-PSO混合算法进行寻优迭代求解。在F(xi)取最小值时,求解式(5)所得基坑土层参数值即为反演得到的最优土层参数值。
“智能”已成为机械加工技术的主要发展方向之一,智能加工是智能制造的重要基础支撑,而加工单元的智能化是智能加工技术的核心内容。随着各主要工业大国对智能制造技术的重视,对智能加工技术的研究也呈现出快速增长态势。从学术论文的发表数量上看,中文文献显著增长的时间出现在近5年,比英文文献的快速增长时间大约滞后10年左右。智能加工中,需要对机床、刀具以及工件的状态进行监测,从而实现整体加工过程最优。其中,视觉技术可以发挥重要作用,具有广阔应用前景。
2 算法基本原理
2.1 粒子群算法
粒子群算法(Particle Swarm Optimization,PSO)最早由KENNEDY J和EBERHART R C[6-7]于1995年提出,通过模拟粒子在解空间中的运动,跟踪个体极值和群体极值来不断更新个体位置,粒子每更新一次位置,就计算一次适应度值,通过比较新粒子的适应度值和个体极值、群体极值的适应度值来不断更新个体极值与群体极值的位置,从而寻找最优解。
2.2 SA-PSO混合算法
粒子群算法后期易受到随机振荡影响,在全局最优搜索中,搜索时间长,收敛速度慢,并易陷于局部极小值。而通过在粒子进行速度与位置更新时引入模拟退火机制,结合退火算法的突跳能力,跳出局部极值区域,避免了易陷于局部极小值问题,可大幅度提高算法性能。SA-PSO混合算法实现步骤如下:
1)初始化参数设置:惯性权重w,加速常数c1和c2,退火起、止温度T和T0以及退火速度k。
2)随机产生n个粒子的种群,即随机产生n个初始解Xi(t),i=1,…,n和n个初始速度Vj(t),i=1,…,n。
3)计算每个粒子的适应值f(Xi(t)),对每个粒子的适应值分别与个体极值pbesti(t)和全局极值gbest(t)进行比较,取优更新为个体极值pbesti(t)和全局极值gbest(t)。
4)根据式(3)和式(4)分别对每个粒子进行位置与速度更新,并将速度限制在最大速度Vmax之内。
5)计算每个粒子更新后的适应值f(Xi(t+1),并计算两个位置所引起的适应值的变化量△E。若△E<0,则接受新位置;若的随机数,也接受新位置,否则拒接。若接受新值,进行降温操作,否则不降温,返回步骤3。其中退火速度k为小于1的数,通常取0.5~0.99,本文取0.98。
2.3 最小二乘支持向量机
最小二乘支持向量机(Least Squares Support Vector Machine,LSSVM)[8-9]作为SVM的一种进化形式,可将其学习问题的求解转化为求解一个线性方程组,避免了求解一个约束凸二次规划问题,大大提高了计算效率。设训练集F由N个样本点构成,则:
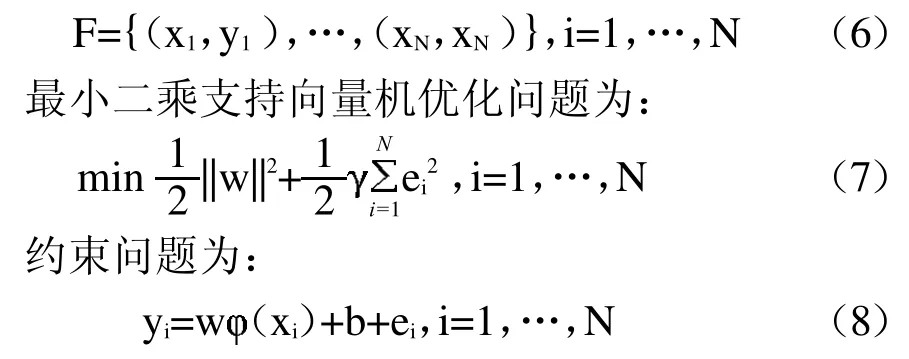

运用KKT条件,令L分别对w,,e,b求偏导并使

其中,En×1=(1,1,…,1)T,n×1=(1,2,…,N)T,Yn×1=(y1,y2,…,yN)T。通过解方程组式(15)可得出 和b的值,故可求出输入样本x与输出样本y的对应关系:

其中核函数选用高斯径向基核函数:

3 工程案例
本文采用昆明市五华区某基坑工程,并选用此基坑的1-1剖面进行反演计算。此剖面的支护形式为桩锚支护,坑顶放坡坡高1.5 m,台宽1.0 m,坡比1∶0.5。支护桩采用桩径为1.2 m,桩长为31 m的旋挖桩,其布置间距为1.5 m,桩顶设置1 200 mm×600 mm的混凝土冠梁。基坑由上至下布置了1排土钉和4排预应力锚索,基坑支护布置和施工工况如图1、表1所示。1-1剖面中支护桩深入9个土层,各层土的物理力学性质指标见表2。

表1 基坑施工工况

表2 土层物理力学参数

图1 基坑支护示意
反分析时,考虑开挖工况为施工过程中最不利工况,选择工况3和工况5进行反分析计算,并选取坑外地面以下2 m(测点1)、3 m(测点2)、4 m(测点3)、5 m(测点4)、6 m(测点5)、7 m(测点6)、8 m(测点7)、10 m(测点8)、12 m(测点9)、14 m(测点10)深度处支护桩的水平位移值作为输出样本。将每层土的物理力学参数当作随机变量,作为输入样本,结合实际扩大取值范围见表3。依据文献[10]均匀试验设计表的构建方法,运用方幂法构建一个18因数30水平的均匀表,利用MATLAB软件进行程序设计,获得均匀表U30(3018),即输入样本见表4。将输入样本数据根据《建筑基坑支护技术规程》(JGJ 120—2012)[11]的相关规定,分别计算出工况3、工况5在不同深度处的位移值,得到输出样本。限于篇幅,只给出工况5的输出样本见表5。

表3 土层参数取值范围

表4 输入样本

表5 工况5输出样本 mm
采用SA-PSO混合算法进行模型参数寻优时,将最大迭代次数设为150,并将其作为算法的终止条件,选择均方误差作为适应度函数,将种群规模设置为50,部分测点模型参数寻优结果见表6。

表6 寻优参数
将寻优后的参数代入最小二乘支持向量机中建立模型,结合目标函数取极小值,不断迭代优化得到最优土层参数值。本文选择c1,c2都为2进行计算,下面给出工况5 2 m、4 m、12 m、14 m的目标函数随迭代次数的变化关系,分别如图2至图5所示。工况3和工况5反演优化结果分别见表7和表8所示。

图2 测点1的目标函数随迭代次数变化

图5 测点10的目标函数随迭代次数变化
分析发现,同一工况下,不同深度测点反演得到的目标函数随迭代次数变化关系相差较大,测点1、测点3的最佳目标函数值明显小于测点测点9、测点10的最佳目标函数值。分析表7,由前3测点分析得到的反演均值、区间差明显优于整体分析的反演均值、区间差和后7个测点组合分析得到的反演均值、区间差,且反演得到的均值与设计值更为接近。分析表8,工况5中的前6个测点获得的土层等效参数反演区间浮动较小,均值也较为靠近设计值,与工况3的分析结果基本一致。对工况3和工况5中③1粉土层及③11黏土层进行对比分析,工况3中前3个测点的反演结果没有后7个测点的反演结果均值接近设计值,反演区间浮动也较大。工况5中③1粉土层反演结果也没有③11黏土层反演结果好,相较于工况3,工况5中③1粉土层反演结果明显更好,但工况3和工况5中③1粉土层及③11黏土层的反演结果与设计值偏差大于前3层土的反演结果。证明开挖面以下土层的反演结果不理想,同时以开挖面以上的测点对开挖面以下土层进行反演,结果差异明显且反演计算结果与设计值相差较大。

表8 工况5土层等效参数反演计算结果

图3 测点3的目标函数随迭代次数变化
工况3开挖面以上反演的土层等效参数均值与工况5开挖面以上反演的土层等效参数均值相差较小且都与设计值较为接近。而开挖面以下的土层等效参数均值差异较为明显且与设计值相差较大,说明此方法不适用于对开挖面以下土层参数进行反演,故基坑开挖面以下土层参数反演还需进一步研究。而以开挖面以上均值替代计算结果发现其与设计值较为接近,证明此方法应用于开挖面以上土层的参数反演是可行的。

图4 测点9的目标函数随迭代次数变化
4 结论
1)将模拟退火算法与粒子群算法结合优化最小二乘支持向量机并应用于基坑土层等效参数的反算是可行的,模拟退火算法与粒子群算法相结合,有效避免了粒子群算法后期收敛速度慢,易陷于局部极小值且不易收敛,提高了算法的运行速度和精度。结果表明开挖面以上反演结果的均值与参数的设计值较为精准的接近,而开挖面以下的反演还需进一步研究。
2)该模型既有支持向量机处理非线性问题的优越性,又具有较好的泛化能力。但模拟退火和粒子群混合算法极大地依赖于相关初始参数取值,针对不同的开挖工况及工程计算案例,需充分结合数据的实际情况进行考虑,可进行多次试算比较选取较为合理的取值或采用广泛已被运用的参考值进行试算。
3)本文在建立最小二乘支持向量机回归模型中选用高斯径向基核函数进行计算,因其具有良好的非线性映射能力、参数数量少、灵活性强等特点。但径向基核函数的全局性能弱,后续研究中可寻找或建立更优化的混合核函数应用于基坑土层参数反演计算中。

