热力站日供热量神经网络预测模型比较与分析

田 野，李 锐，董 妍，王嘉明

(1.北京建筑大学 环境与能源工程学院，北京 100044； 2.北京市热力集团有限责任公司，北京 100026)

1 概述

精准预测热力站日供热量，无论对节能减排还是对提升供热质量，都具有重要意义。许多学者提出了不同预测方法，如灰色预测法、回归分析法、神经网络法等[1]。神经网络预测作为一种预测方法已经被大量应用于热负荷预测，神经网络的特点是无需建立复杂的输入输出关系，在非线性问题的处理上表现更好[2]。康胜文[3]在进行热负荷预测时，比较了回归分析法与神经网络法，认为神经网络法更具有优势。宋军等人[4]通过研究分析指出，BP神经网络基本满足了短期热负荷预测的要求。李思琦等人[5]改进了神经网络，得到了更加精确的热负荷预测模型。

本文以北京某热力站运行数据、气象参数为样本，采用BP神经网络，建立日供热量预测模型，对输入变量、隐含层神经元数量的影响进行分析。

2 预测模型

BP神经网络具有非线性映射能力、泛化能力、容错能力，因此本文采用BP神经网络建立热力站日供热量预测模型。BP神经网络结构包括输入层、隐含层、输出层[6]。输出层神经元数量为1，输出变量为热力站日供热量。

输入变量的选取，影响着预测模型的预测效果。输入层神经元数量(即输入变量数量)过少无法达到预期效果，数量过多虽然会提高计算精度，但易使神经网络结构过于复杂，训练时间延长。热力站日供热量受多种因素影响，可分为气象因素、系统因素。气象因素包括室外温度、相对湿度、大气压力、风速等。系统因素指供热系统的特性，包括前几日的供热量等[1]。分析北京某热力站运行数据发现，室外温度、风速与供热量存在相关性。因此，将日平均室外温度、日平均风速、前1日供热量作为必要的输入变量。在此基础上，增加日最低室外温度、日最高室外温度、日平均相对湿度、大气压力、前2日供热量、前3日供热量，分别建立预测模型1～3。隐含层神经元数量设定为10，预测模型1～3输入变量见表1。

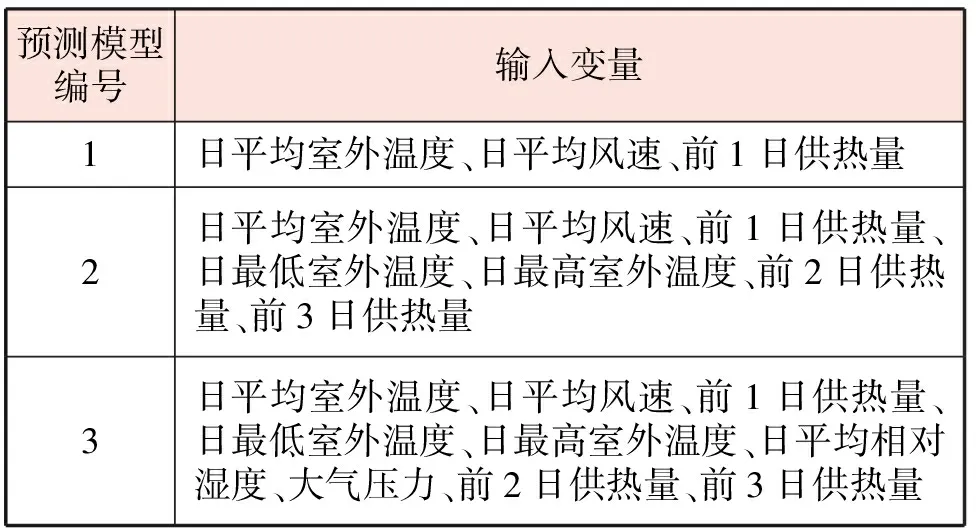
表1 预测模型1～3输入变量

隐含层神经元数量决定了神经网络的计算能力。隐含层神经元数量过少，神经网络的计算能力不足，预测结果易发生欠拟合。隐含层神经元数量过多，预测结果易发生过拟合，使预测模型缺乏泛化性[7]。目前，大多采用经验公式与试凑法相结合的方式来确定隐含层神经元数量[8]。为分析隐含层神经元数量对预测结果的影响，输入变量与预测模型2一致，改变隐含层神经元数量，分别建立预测模型4～16(见表2)。实际上预测模型11与预测模型2一致，为不破坏预测模型4～16的连续性，仍保留预测模型11。

表2 模型4～16隐含层神经元数量

3 研究对象

热力站供热面积为88 711 m2，站内设置了热量表以及供水温度、回水温度、流量传感器。除供热量、供回水温度、流量外，监测数据还包括室外温度、风速等，每隔5 min采集1次数据，以日为单位对数据进行整理。选取2017—2020年供暖期数据进行研究，并对异常、缺失严重的数据进行处理，最后得到357个供暖日的有效数据。随机将70%的样本作为训练集，15%的样本作为验证集，15%的样本作为测试集。采用最大最小值归一化法将输入数据归一化到[-1，1]。利用MATLAB软件建立BP神经网络预测模型。

预测模型的预测效果评价指标为拟合优度、均方根误差(RMSE)、平均绝对百分比误差(MAPE)。拟合优度通过决定系数R2度量，决定系数越接近1，预测模型的拟合效果越好。均方根误差反映预测结果相对于实际结果的平均偏差情况，用于评价预测模型的稳定性，均方根误差越小说明预测模型的稳定性越高。平均绝对百分比误差可以反映预测结果的可信程度，平均绝对百分比误差越小，说明预测结果可信度越高。

决定系数R2、均方根误差σRMSE、平均绝对百分比误差σMAPE的计算式分别为：

式中R2——决定系数

n——样本数量

Qi,p——热力站日供热量预测值，GJ

Qi,m——热力站日供热量实际值，GJ

Qm,av——全部样本实际值的平均值，GJ

σRMSE——均方根误差，GJ

σMAPE——平均绝对百分比误差

4 预测结果与分析

4.1 输入变量的影响

预测模型1～3部分样本日供热量预测值与实际值见图1。样本来自测试集。由图1可知，在预测模型1～3中，预测模型2日供热量预测值与实际值最接近。

图1 预测模型1～3部分样本日供热量预测值与实际值

预测模型1～3的决定系数、均方根误差见表3。由表3可知，在预测模型1～3中，预测模型2的决定系数最接近1、均方根误差最小，说明模型2的预测效果最佳。预测模型1的预测效果最差，预测模型3的预测效果介于预测模型1、2之间。

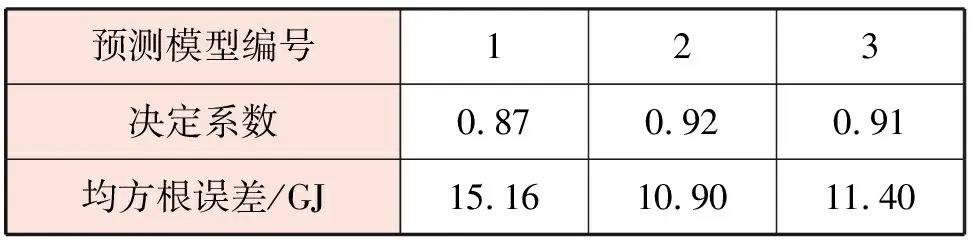
表3 预测模型1～3的决定系数、均方根误差

在隐含层神经元数量设定为10条件下，输入变量为日平均室外温度、日平均风速、前1日供热量、日最低室外温度、日最高室外温度、前2日供热量、前3日供热量时，预测模型的预测效果最佳。输入层神经元数量为3时，由于输入变量不足，预测模型的预测效果最差。

4.2 隐含层神经元数量的影响

预测模型4、5、11、14、16部分样本日供热量预测值与实际值见图2。样本来自测试集。由图2可知，预测模型16日供热量预测值与实际值的吻合度最好。

图2 预测模型4、5、11、14、16部分样本日供热量预测值与实际值

由计算结果可知，从决定系数、均方根误差评价预测模型4～16的预测效果比较困难。因此，采用平均绝对百分比误差来评价模型的预测效果，预测模型4～16的平均绝对百分比误差见表4。由表4可知，预测模型16的平均绝对百分比误差最小，说明隐含层神经元数量为15时，预测效果最好。

表4 预测模型4～16的平均绝对百分比误差

当输入变量为日平均室外温度、日平均风速、前1日供热量、日最低室外温度、日最高室外温度、前2日供热量、前3日供热量时，隐含层神经元数量达到最多时(为15)的预测模型16预测效果最佳。隐含层神经元数量并非越多越好，在实际应用中，应选取多个隐含层神经元数量，根据预测效果选取合适的隐含层神经元数量。

5 结论

① 当隐含层神经元数量设定为10，输入变量为日平均室外温度、日平均风速、前1日供热量、日最低室外温度、日最高室外温度、前2日供热量、前3日供热量时，预测模型的预测效果最佳。输入层神经元数量为3时，由于输入变量不足，预测模型的预测效果最差。

② 当输入变量为日平均室外温度、日平均风速、前1日供热量、日最低室外温度、日最高室外温度、前2日供热量、前3日供热量时，隐含层神经元数量达到最多时(为15)的预测模型预测效果最佳。隐含层神经元数量并非越多越好，在实际应用中，应选取多个隐含层神经元数量，根据预测效果选取合适的隐含层神经元数量。