基于ARIMA-LSTM的能量预测算法

沈露露，梁嘉乐，周 雯

(南京林业大学 信息科学技术学院，江苏 南京 210037)

0 引言

随着物联网信息技术(Internet of Things, IoT)的发展，无线传感器网络(Wireless Sensor Networks, WSN)成为物联网中的重要组成部分，并且融入了传感器技术、无线通信技术、微机电系统以及分布式大规模数据信息管理等前沿技术，使得无线传感器网络的应用越来越广泛[1-2]。传统的无线传感器网络是将环境能量作为传感器节点工作运行的动力，然而环境所能提供的能源存在许多不确定的因素，这对无线传感器网络的传输可靠性及性能带来了巨大的挑战。为了最大化地利用采集到的能量和节省路由协议中的能耗浪费，可以运用能量预测算法提前预测未来能量[3-6]。能量预测算法通常使用有关未来能源中短期变化的信息作为基础样本来预测未来能源的使用，使系统既能够长时间稳定工作，又可以降低能源的浪费[7]。

为了减少无线传感器网络在传输过程中的能源浪费、提高网络的能源效率，可以通过基于统计学原理、机遇随机原理和机器学习原理的方法进行能量预测，这吸引了国内外学者广泛的研究和探索[8-13]。文献[8]对能量采集传感器网络中的功率管理进行了研究，提出了指数加权移动平均算法(Exponential Weighted Moving Average, EWMA)，它的主要作用是当一天中的一段时间内收集到的能量与前一天同一时间段收集到的能量相似时，可以近似地将该时间段收集到的能量看做前几天同一时间段收集到能量的加权平均和。文献[9-10]针对EWMA算法中还存在着气候状态变化对预测结果的影响，专门提出了可以根据不同的天气情况进行修正预测结果的EWMA算法，比如气候条件移动平均算法(Weather-conditioned Moving Average, WCMA)和天气条件移动平均算法(Weather-conditioned Selective Moving Average, WCSMA)。文献[11]创新地通过对比过去的能量资源使用情况，设计更精准预测未来能量使用情况的轮廓能量(Profile Energy,Pro-Energy)预测模型来进行太阳能的能量预测。文献[12]考虑了节点采集能量的稳定性和网络稳定的信息传输，提出了一种基于长短时记忆递归神经网络(LSTM-RNN)的网络预测模型。文献[13]主要讲述了将神经网络和小波变换两种方法相结合的混合模型，并通过预测太阳能能量来验证其模型的有效性。

在复杂多变的环境中，传感器节点采集得到的太阳能时间序列既呈现线性因素又呈现非线性因素，给能量预测带来了困难。自回归积分移动平均(Autoregressive Integrated Moving Average，ARIMA)算法适合处理线性序列而长短期记忆(Long Short Term Memory， LSTM)算法更加适合处理非线性时间序列，因此，本文综合二者特点，提出了ARIMA-LSTM的组合预测模型，以期提升能量预测的精度。具体来说，先将太阳能序列用ARIMA模型进行预测，然后将预测得到的残差值代入LSTM神经网络模型，得到残差的新预测，用以修正ARIMA模型的预测结果。仿真结果显示，相比于单一的预测模型算法，所提出的组合预测模型算法具有更高的准确性与更低的误差。

1 现有算法与设计思路

本文针对太阳能辐照强度的短期预测问题进行了研究。先介绍ARIMA算法[14]和LSTM算法[15]，然后提出了ARIMA-LSTM的组合预测模型。

1.1 ARIMA算法

ARIMA模型是一种时间序列预测模型，是由自回归(AR)模型和滑动平均(MA)模型所构成。它与自回归移动平均(ARMA)模型同属于自回归模型，但是二者对于数据的要求大相径庭，ARMA模型适用于平稳时间序列的数据，而ARIMA模型则更适用于差分后为平稳时间序列的数据。由此也可称ARIMA模型为差分时间序列的ARMA模型。p、d、q是ARIMA模型中的主要参数，其中，p表示自回归阶数，d表示原始序列平稳化需要的差分阶数，q则表示移动平均阶数，因此可以将ARIMA模型简写成ARIMA(p,d,q)。该模型先通过d阶差分将非平稳时间序列Yt转化为平稳时间序列Xt，然后使用ARMA(p,q)对平稳时间序列Xt进行拟合。ARMA(p,q)模型的数学表达式为：

(1)

式中，自回归系数由φi(i=1,2,…,p)表示，滑动平均系数用θj(j=1,2,…,q)表示，残差值参数表示为εt。

自相关函数(ACF)和偏自相关函数(PACF)可以用于测量当前序列值和过去序列值之前的相关性，并指示预测将来值时最有用的过去序列值。自相关函数表示当延迟为k时，相距k个时间间隔的序列值之间的相关性，而偏自相关函数则表示在考虑间隔之间值的同时，延迟为k时相距k个时间间隔的序列值之间的相关性。

ARIMA(q,d,p)的模型参数取值范围可以通过ACF与PACF来确定，也可以借助赤池信息准则(AIC)和贝叶斯信息准则(BIC)来计算模型的检验值，最后又基于最小信息准则确定最优模型并进行预测。

k值的大小和模型的复杂程度与极大似然函数L成正比关系，与AIC的值则成反比关系。随着k值增大，模型的复杂度提高，极大似然函数值L也会增大，AIC值减小；若k值过大，则导致AIC值增大，ARIMA算法模型呈现过拟合的现象。

由于AIC依旧存在设计缺陷，所以又在AIC的基础上提出了BIC，BIC与AIC相似，BIC的值越小，算法模型就越合理。

1.2 LSTM深度学习算法

LSTM深度学习算法与递归神经网络(Recurrent Neural Network, RNN)的不同之处在于前者在后者的基础上加入了细胞状态和门结两个结构[16-17]以此来预测太阳能辐照强度，通过对比可发现LSTM模型的表现比时间递归型神经网络和隐马尔科夫模型的表现更好。

传统的RNN在解决时序长相关问题时存在梯度消失和梯度爆炸的问题，而细胞状态的作用是将具体信息连续地传递到RNN上，因此能够有效解决传统RNN存在的问题。LSTM是基于门控制单元结构的深度学习模型，通过遗忘门、输入门和输出门这三种门类型控制传输信息[18]。LSTM神经网络如图1所示，方框内是单个神经元细胞结构，c表示神经元细胞的状态值，h表示神经元细胞的输出值。LSTM神经网络细胞的结构如图2所示。

图1 LSTM神经网络

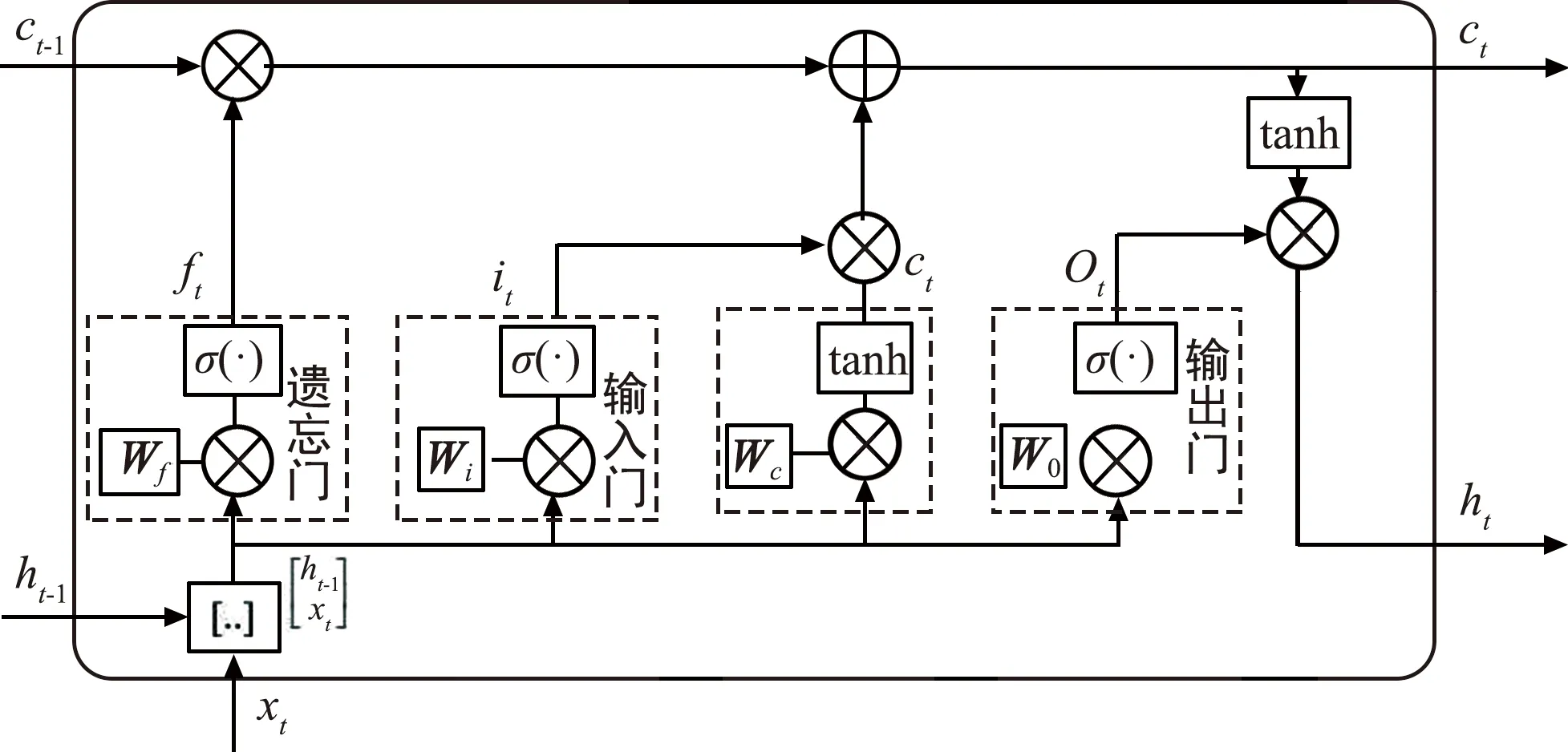
图2 LSTM神经网络细胞的结构

遗忘门的作用是决定保留或删除时间序列中前一刻输出的ht-1中的信息，计算公式如下：

(2)

式中，Wf表示遗忘门的权值，上标T表示转置，bf表示遗忘门的偏置，σ(·)表示sigmoid激活函数，表达式为：

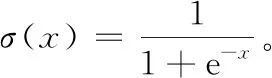
(3)

(4)

(5)

式中,Wi表示输入门的权值,上标 T 表示转置；bi表示输入门中的偏置,Wc表示tanh函数中的权值,bc表示tanh函数中的偏置。

(6)

t时刻的单元状态ct的表达式为：

(7)

输出门可以决定输出信息的多少，并将记忆模块信息传递给下一时刻存储模块。LSTM模型利用输出门和一个tanh函数来输出ht。

(8)

ht=Ottanh(ct)，

(9)

式中，W0表示输出门的权值，b0表示输出门中的偏置。

LSTM时间序列预测模型先将时间序列数据划分为训练集和测试集两种验证集，然后对数据进行预处理，之后设置模型的初始参数以及损失函数后对预测模型进行训练，最后对训练模型进行预测。

1.3 基于ARIMA-LSTM组合预测模型

太阳辐照的变化是复杂多样的，既有线性变化趋势，也有非线性变化趋势，采用单一的能量预测模型进行预测会导致模型的拟合结果不佳。为了更好、更精准地预测能量，本文结合ARIMA模型和LSTM模型设计出基于ARIMA-LSTM的组合预测模型。

组合模型首先将采集的太阳能序列用ARIMA模型进行预测，而后将残差值代入LSTM神经网络模型，得到关于残差的预测，修正ARIMA模型的预测。具体的，首先利用ARIMA模型筛选和过滤太阳辐照数据中线性趋势预测结果，而非线性趋势，则保留在ARIMA模型的残差值中；然后将残差值传送到LSTM模型，再由LSTM模型训练输出非线性趋势的误差预测结果；最后将两个模型的预测结果进行叠加，得到组合预测模型预测结果。组合预测模型的工作过程如图3所示。

工程主要由路基、桥涵、隧道、立交及附属设施等组成，属大型新建项目，采用四车道一级公路技术标准，设计车速60 km/h，整体式路基宽度23 m，上下行隧道进出口段分离式路基宽度11.25 m。全线设特大桥7座17 032.5 m，其中跨黄河特大桥3座、顺黄河特大桥4座；大桥22座5 872.5 m，其中跨黄河大桥1座（盐锅峡黄河大桥）、顺河或跨沟大桥21座；中桥7座396.58 m；小桥4座86.86 m；隧道2座3 255 m(以单洞长度计)；涵洞123道3 474.87 m；半互通式立体交叉4座，公铁立交1处，平面交叉35处；主线收费站1处，养护工区1处，隧道管理站1处，管理所1处。

图3 ARIMA-LSTM组合预测模型结构

(10)

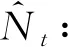
(11)

式中，f(·)为LSTM模型的关系函数，εt为误差值。

最终根据ARIMA模型的预测值叠加LSTM模型输出的残差预测值，计算出组合模型的预测值：

(12)

需要说明的是，本文采用的方式是迭代预测，即模型预测下一时刻太阳辐照值是以上一时刻预测值的预测模型为基础进行的。即ARIMA-LSTM组合模型应用于能量预测实际场景时，下一个时间点的预测值都是每个采集到的能量信息通过网络历史数据训练后得到的。

2 仿真结果

2.1 仿真数据和评价指标

本文所使用的数据来自美国可再生能源实验室 (NERL)[20]网站的太阳辐照数据，实验过程中采用2019年6月20日—11月20日的太阳辐照数据。为了避免异常值对实验的干扰，例如正午时刻太阳辐照为0 W/m2，本文采用箱型图分析的方法来减少一些特殊因素对实验的干扰，原理是当数据超过或不足实验设定的上下界值时，该数据将被认定为异常值，然后再通过平均值来校正已经被判定的异常值。

对于结合了ARIMA和LSTM两种算法的组合能量预测算法，可以如同LSTM模型一样将数据划分为训练级和测试集。本文首先选取总数据前90%的数据作为训练集，后10%的数据则作为测试集，然后将模型预测结果与实际值进行比较。为了检验三种能量预测模型的准确性，本文采用归一化平均方根误差(NRMSE)、归一化平均绝对偏差(NMAE)来检验模型的精确度，公式如下所示：

(13)

(14)

式中，Fi表示第i个预测值，Ri表示第i个真实值，n代表样本点的个数。

综上，归一化平均方根误差和归一化平均绝对偏差越小，基于ARIMA-LSTM组合预测模型的结果就越精确。

2.2 模型参数设置

图4是经过预处理后的数据。预处理是指通过格拉布斯检验法，对超出所设界限的异常值进行检验并通过平均值进行修正。由图4可见，连续480 h采集到的太阳辐照在不同的时间段具有不同的均值且数据波动很大，例如在第90时采集到的辐照强度接近800 W/m2、而第100时采集到的辐照强度为0 W/m2。考虑到非平稳序列是指包含趋势、季节性或周期性的序列，可以看出数据是具有周期性的非平稳随机序列——连续480 h采集到的数据呈现波浪形的波动。

图4 连续480 h采集太阳辐照图

由于ARIMA模型适用于平稳序列的数据，所以需要采用差分方法将非平稳数据转化为平稳数据，将原始数据进行一阶差分后的数据如图5所示。

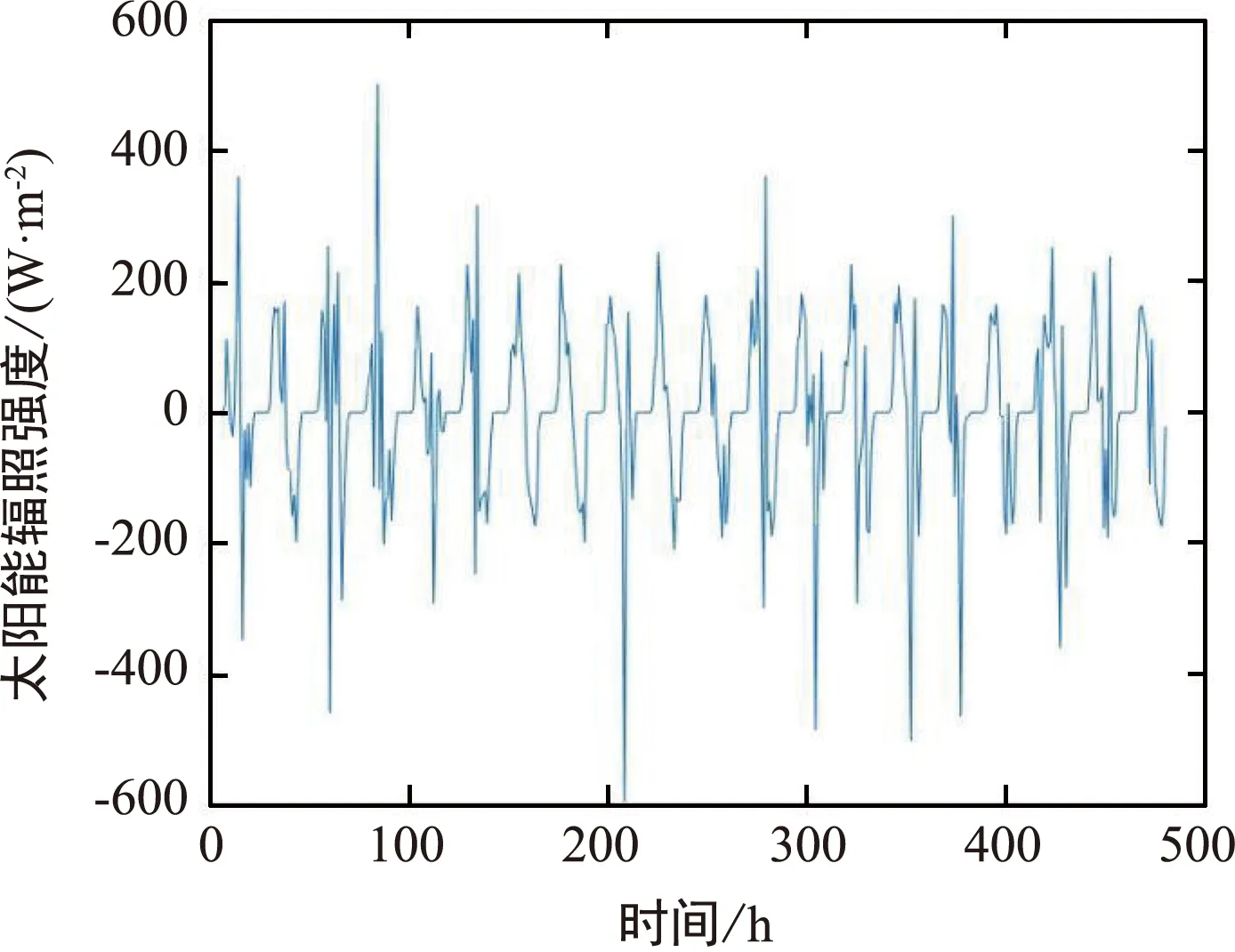
图5 一阶差分后的数据图

从图5中和通过Matlab自带的平稳性检验方法ADF和KPSS，可以看出一阶差分后数据呈现平稳化，因此可将模型阶数d设为d=1。然后通过ACF图和PACF图来判断模型参数p和q的最大值，如图6所示。可以发现，模型的ACF图和PACF图分别在三阶和二阶后截尾，因而可以得知参数p和q的最大值分别设为2和3。

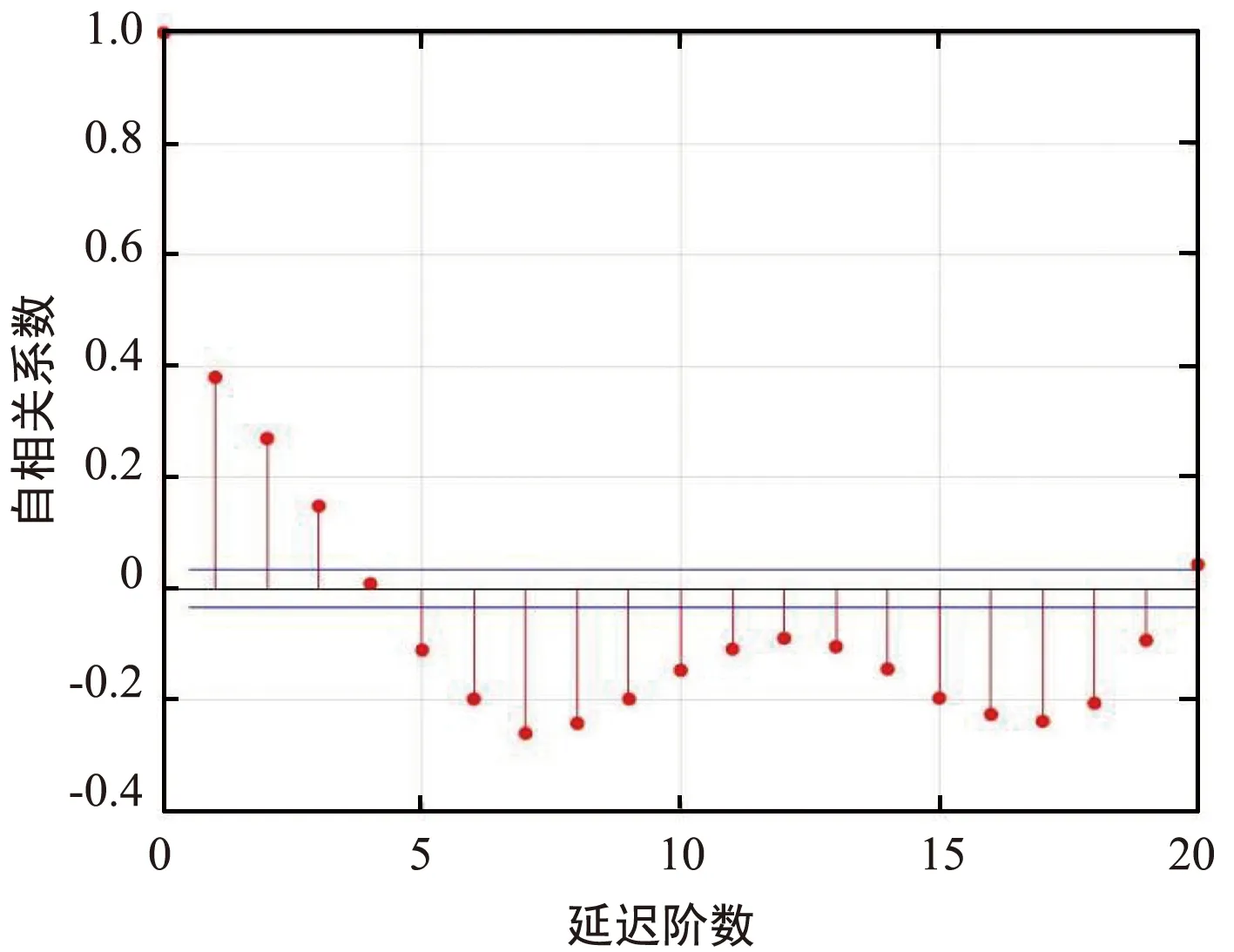
(a) ACF图

再计算模型的AIC值和BIC值可以发现，当ARIMA(p,d,q)模型的参数组合为(2,1,3)时，能量预测模型的AIC值和BIC值较小。AIC值和BIC值越小表示算法模型越合理，能量预测精度越准确，所以本文最终选取参数组合(2,1,3)。此时自回归系数φ≜[φ1φ2]T=[-1.69 0.97]T，滑动平均系数θ≜[θ1θ2θ3]T=[1.95 -1.38 0.22]T。

经过ARIMA预测模型得到的残差值序列(记为{et})再通过LSTM模型进行预测。LSTM模型的参数如表1所示。需要说明的是，在迭代的前半段，为了快速地找到一个初步的预测值，采用初始学习率0.005；但是在迭代的后半段，把学习率调整为初始学习率的1/5，进行预测值的细微调整，提升预测精度。

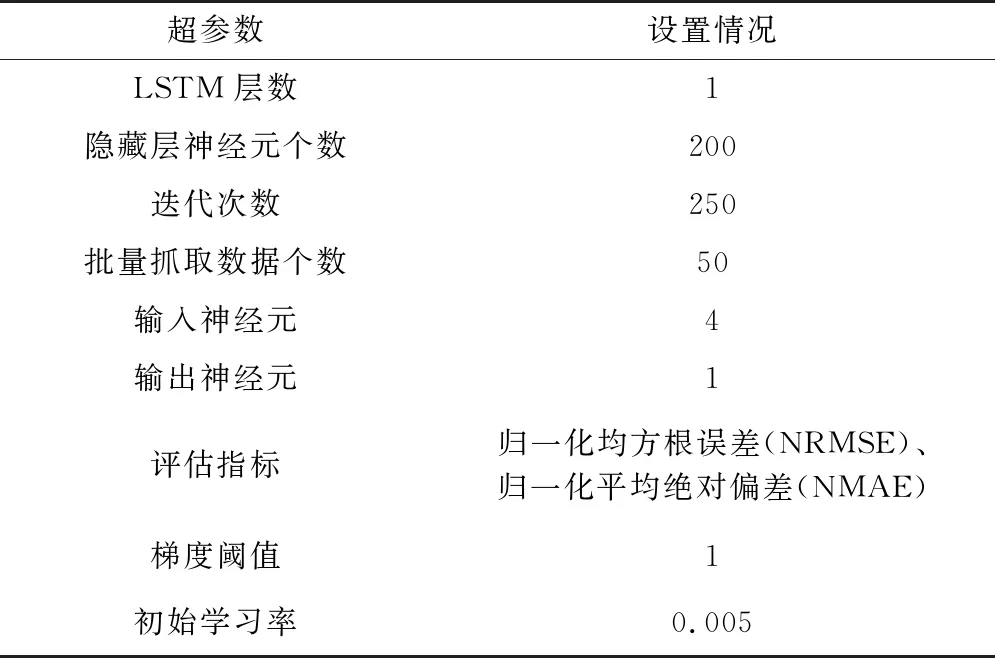
表1 LSTM能量预测模型的网络参数

2.3 仿真结果对比

利用Matlab软件编译、运行提出的ARIMA-LSTM组合预测模型，得到预测结果。为了能够直观地看出组合模型的合理性和优点，本文从运行时间和精确度两方面添加了ARIMA、LSTM两个单一预测模型作为对照组。图7对比了三种能量预测模型的太阳能序列预测性能。可以看出，ARIMA算法在太阳辐照为0时的预测值误差较大，这是由于此时的原始数据不稳定，而ARIMA模型在预测时序数据时，必须是稳定的数据，否则预测的结果会不准确。还可以看出，LSTM能量预测模型优于ARIMA能量预测算法，具有更好的预测精度。在三种预测模型中，本文提出组合预测模型性能最好，平均误差最小。

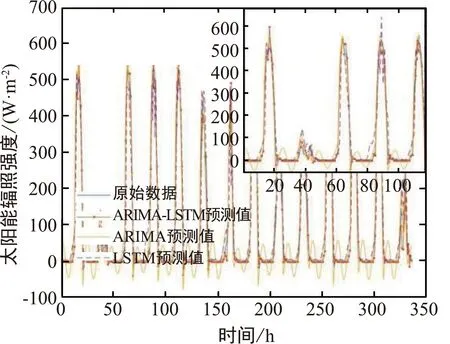
图7 三种能量预测模型的对比图

三种能量预测模型的运行时间如表2所示。其中，训练时间是对模型进行参数训练的时间，运行时间是用模型进行正式预测的时间，总时间是二者之和。仿真平台具体参数为：Windows11操作系统、8核3.2 GHz CPU、Matlab R2018，太阳能序列的预测长度设置为348。由表2可知，三种模型的运行时间相当，约0.156 s。ARIMA模型在预测时只需要对上一时刻的数值进行简单的加、乘运算，不需要进行提前训练，因此训练时间为0，总时间最短。而LSTM和提出的算法都需要提前训练LSTM模型参数，然后才进行预测，因此二者的总时间较长。

表2 能量预测模型运行时间评估

表3对比了三种模型的NRMSE和NMAE。可见，ARIMA模型预测准确性最低，其NRMSE、NMAE值均比另外两个模型高，ARIMA模型的NMAE为0.375 2，高于LSTM模型的0.305 2和提出模型的0.289 6。提出模型的NRMSE值和NMAE值是三种预测模型中最低的，提出模型的NRMSE为0.050 9，低于LSTM的0.077 6和ARIMA的0.107 2。总之，提出模型的预测精度最高。

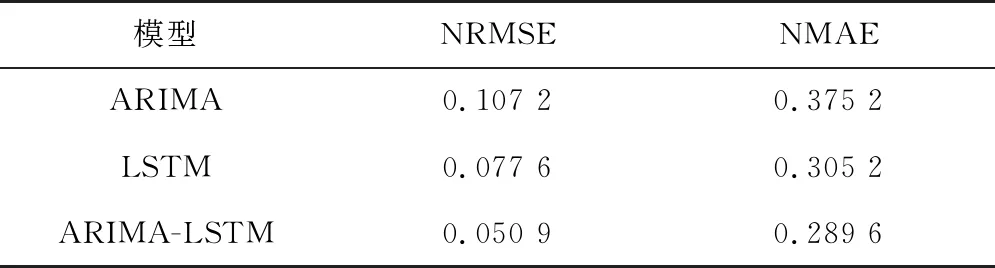
表3 模型预测结果评估

总而言之，通过对三种能量预测模型的精度和运行时间的比较，可以发现，ARIMA模型的运行时间最小，但是精度最差；提出的组合模型在运行时间方面和LSTM模型相当，但是具有更好的预测精度。

3 结束语

本文研究了无线传感网络的太阳能能量预测问题，提出了基于ARIMA-LSTM的组合预测模型，以期提升能量预测的精度，合理规划能量的使用。首先，将包含线性因素和非线性因素的非平稳能量采集数据转化为平稳数据序列，用ARIMA模型预测序列中的线性分量；然后提取非线性残差的分量，用LSTM模型预测下一步的残差分量；最后将二者的预测结果进行叠加，得到整个数据序列的预测值。仿真比较了提出模型、ARIMA模型和LSTM模型的精度和运行时间，结果表明ARIMA模型的运行时间最小，但是精度最差；提出模型在运行时间方面和LSTM模型相当，但是具有更好的预测精度。提出的预测模型结合了ARIMA模型和LSTM模型的优点，不仅适用于太阳能的预测，也可能推广到其他类型能源，如风能、振动能的预测中。