基于云边协同算力调度的高效边缘卸载研究
王姗姗,罗志勇
(中山大学 电子与通信工程学院,广东 深圳 518107)
0 引言
车载边缘计算(Vehicular Edge Computirg, VEC)网络因其广泛的应用而备受关注[1]。然而,有限的车载设备资源无法支持越来越多对低延迟和高性能服务需求的新应用,如信息服务、路径导航、娱乐应用等。为了应对这一挑战,基于云边端一体化与智能协同等算力网络技术的车载边缘计算作为一种新型计算范式。VEC网络将分布式的计算节点连接起来,动态实时感知计算与通信资源,进而实时统筹分配和调度计算任务,形成了一张计算资源可感知、可分配、可调度的网络,满足了用户车辆任务对算力的要求,也是边缘计算向泛在算力网络融合演进的新阶段[2-3]。对于用户车辆与边缘服务器之间进行通信时,计算任务可被卸载到边缘服务器上,在这个过程中VEC网络会产生时延与能耗等方面的开销。为了满足VEC网络中大量用户的多样化业务需求,基于云边协同、多点算力均衡等算力网络技术,设计高效的计算卸载策略来实现对计算和网络资源状态的感知,进而实现资源的按需调配与调度,从而在算力网络中实现更快通信、更高感知、更准计算。
1 背景介绍
近年来,一些专家对VEC网络的计算卸载策略开展了研究。Yang等人[4]研究了面向智能物联网的多层算力网络,通过考虑海量计算之间的交互与算力资源协同,实现了算力的智能分发。Luo等人[5]为提高VEC网络的任务卸载率,提出了一种基于贪心匹配的动态任务卸载算法。澳大利亚悉尼大学计算机学院[6]提出了基于联邦学习的无线网络联合优化模型,通过建立节点间分布式算力分配,为解决通感算一体化系统中节点算力不足与不均衡的问题提供了解决思路。然而,这些研究仅从移动终端架构的角度分别优化了卸载决策或资源配置,并没有充分利用云中心和MEC服务器的异构计算能力,导致算力网络中仍然存在算力分配不充分和不均衡的问题。
与此同时,鉴于VEC网络的动态性和随机性,现有的计算卸载策略大多需要引入更加智能的算法来应对传统数学方法的不足, 并实现网络的通信、计算和存储资源的智能管理[7-9]。美国康奈尔大学的学者[10]采用在线优化方法实时学习并更新系统参数来优化网络吞吐量。Leng等人[11]提出了一种基于云计算的智能车联网管理系统,增强了车辆的实时感知功能。但这些研究仅适用于静态网络环境,即在执行卸载决策后不再同步更新资源的分配。
由以上的分析可知,目前VEC网络中基于云边协同的任务卸载与资源分配策略存在以下不足:① 大多没有考虑同时利用云中心、边缘服务器的异构计算能力,且集中在单一边缘节点的通感、通算、感算等双边能力的一体化方面;② 虽然计算资源呈现出泛在部署的趋势,但是边缘节点与云计算节点之间缺失有效的算力协同机制;③ 联合任务卸载决策与资源分配的研究大多是针对静态的,执行卸载决策后未同步更新资源分配。
基于此,为了更加高效利用网络边缘侧的海量分布式算力资源,本文针对6G通感算融合网络中边缘节点缺失智能化处理的问题,将算力与网络深度融合,基于协同分布式计算资源提出了一种云边协同智能驱动车载边缘算力网络架构,其中车辆可以将计算密集型和时延敏感型任务分别卸载到MEC服务器、聚合服务器和云中心三个层次上,实现业务在各级节点的算力最优。 通过结合实时计算负载与网络状态条件,动态地将计算任务卸载到最佳的边缘节点上权衡用户任务卸载策略,实现多点算力的最优均衡。考虑以最小化系统长期总成本为目标,联合任务分配和资源分配策略建模为优化问题,并将该优化问题转化为马尔可夫决策过程(Markov Decision Process, MDP)。最后,利用云边协同的深度Q网络(Cloud-Edge Collaborative Deep Q-Network,CEC-DQN)算法解决MDP问题,实现了任务的灵活分配和资源的智能管理。仿真结果表明,所提出的计算卸载策略优于基准策略,能够有效降低系统的总长期开销,最终实现单点算力的有效利用与多点算力的最优均衡调度。
2 系统模型
2.1 VEC 网络架构
本文针对VEC网络中边缘节点缺失智能化处理的问题,基于云边端协同与分布式算力调度等技术提出了一种分层协同智能驱动VEC网络架构,如图1所示。任务模型为整体任务卸载模型,IoV用户可以将任务整体卸载到 MEC服务器、聚合服务器和云中心三个层次上权衡卸载策略。IoV用户层包括行驶在道路上的I类车辆,车上配备了多种传感器,可以用于感知物体的距离、角度等环境状态信息,便于车辆做出可靠的研判。在VEC系统中,考虑的场景是一条双向的车道,在车道一侧部署了配有边缘服务的路边单元(Roadside Unit,RSU)构成边缘层。每个RSU优先与通信范围内的用户通信,每个用户在t时隙只能与一个RSU关联。为了简化模型,重点考虑单个RSU的模型,该解决方案可以拓展到多个RSU的情况。聚合服务器层比MEC服务器具有更好的计算资源,可以通过有线连接与多个RSU通信。此外,计算任务还可通过MEC服务器使用有线方式转发到云服务层进行卸载。聚合服务器与云服务器作为MEC服务器的补充方案,可以满足大量用户的计算卸载需求,但是会消耗更多的时延与能耗。

图1 云边协同智能驱动VEC算力网络架构
2.2 任务模型
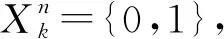
在云边协同VEC网络中,用户采用正交频分多址接入技术(Orthogonal Frequency Division Multiple Access,OFDMA)与边缘节点进行通信。不同的用户车辆占用不同的信道进行双向传输,每一个子信道的带宽为b。假设在某一道路段内,各个用户车辆与边缘节点之间的通信干扰可以忽略不计,则根据香农定理,计算任务n与边缘服务器之间的最大数据传输速率为:
(1)

(2)
若任务n需要通过有线连接卸载到聚合服务器上,则传输时延定义为:
(3)
式中,Ras为聚合服务器上的数据传输速率。若任务n需要通过有线连接方式将计算任务卸载到云服务器上,则将Ras替换为云服务器上的数据传输速率Rcs。
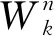
(4)
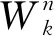
当计算任务n执行计算卸载时,一般经历以下三个阶段:任务上传、任务执行与结果反馈。因为结果反馈阶段的数据一般要比上传的数据小很多,所以本文忽略结果反馈的时延。
因此,计算密集型任务n的处理总时延Tn可以根据通信与计算模型得到:
(5)
计算密集型任务n总能耗可以表示为:
(6)
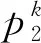
为了考虑用户针对不同的计算卸载场景对时延与能耗的偏好,考虑增加权重因子θ∈[0,1],来权衡时延与能耗的重要性。构建系统成本函数如下:
Gn(t)=θTn(t)+(1-θ)En(t)。
(7)
3 问题形成
本研究旨在动态、随机的VEC系统中,针对有限的网络资源与大量车载用户需求之间的矛盾,通过基于云边端一体化与分布式算力调度技术联合优化设计任务卸载与资源分配策略,来最小化VEC系统在长期一段时间内的总成本函数,并解决通感算网络中边缘节点算力不足与分布不均衡的问题。因此目标函数如下:
(8)
C6:Tn≤τ, ∀n∈N。
(9)
4 基于CEC-DQN的计算卸载策略
4.1 MDP 定义问题
由于P1属于混合整数非线性规划(MINP)问题,为了保证问题的长期随机优化特性,本文将P1转换为MDP[12-13]。MDP一般是由三个关键要素组成,即M= {State,Action,Reward}。其中,State为一个有限的状态集合,Action为一个有限的动作集合,Reward为即时奖励函数。通过结合具体的优化P1,给出了三个关键要素具体化的定义。
(1)State
在t时隙时,系统状态包括所有车辆任务卸载的卸载请求、MEC服务器、聚合服务器和云服务器的计算资源、系统带宽。因此系统状态空间可以定义为s(t) = (at,bt,fk=1(t),fk=2(t),fk=3(t),B(t)),其中,at为待卸载任务数据量大小,bt为待卸载任务所需要的计算量,fk=1(t),fk=2(t),fk=3(t)分别为MEC、聚合服务器和云服务器的计算资源,B(t)为在时隙t时的带宽资源。
(2)Action

(3)Reward
由于优化问题P1的目标是最小化系统长期总成本,所以将t时隙的即时回报奖励函数设计如下:
(10)
式中,G(MEC)表示所有任务在MEC服务器上执行卸载时系统的总成本,G(s,a)表示基于当前状态和动作执行后的系统总成本。
4.2 CEC-DQN 方法
随着状态空间和动作空间的增加,传统Q-learning算法会产生巨大的时间开销[14]。为避免这一问题,本文采用了一种基于CEC-DQN的高效计算卸载策略[15-16]。CEC-DQN算法的核心思想是将Q网络作为VEC网络中的策略评价准则[17],利用神经网络对不同状态的动作组合下的Q值进行近似估计,将Q表的更新转化为函数拟合问题[18],即
Q(s,a;θ)≈Q(s,a)。
(11)
为了打破数据的相关性和保证训练的稳定性,DQN算法引入经验重放与双网络(预测网络、目标网络)机制,大大提高训练的效率。神经网络的更新是通过最小化损失函数获得的。损失函数采用均方误差函数,表示如下:
Loss(θ)=E[(y-Q(s,a;θ)2],
(12)
式中,y通过目标网络生成,其计算公式为:
y=r+maxQ(s′,a′;θ′)。
(13)
VEC网络中基于CEC-DQN的计算卸载策略如图2所示。CEC-DQN的训练伪码由算法1给出。
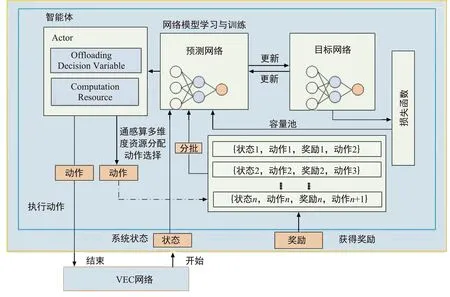
图2 基于DQN的任务卸载和资源分配算法

算法1 DQN计算卸载策略1: 初始化经验池R的大小为N2: 初始化预测Q网络以及随机权重参数θ3: 初始化目标网络Qtarget以及随机权重参数θ'=θ4: for episode=1 to M do5: 初始化状态 so6: for step =1 to T do7: ActionSelectionat=Random a,p=1-∈argmax(Q(st,a;θ)),p=∈ 8: 执行at, 计算 rt,并观察下一个状态st+19: 将经验et=(st,at,rt,st+1)存储到经验池R10: 从经验池R中随机抽取minibatch经验为Rτ11: 计算目标Q值y = r + max(s',a';θ')12: 计算损失函数,并通过最小化损失函数来更新预测网络的参数θ13: Y轮迭代以后复制参数θ来更新目标网络参数即Qtarget=Q14: end for15: end for16: 保存训练的目标网络参数
5 性能评估
在VEC网络中,考虑了一个RSU和多个IoV用户的场景,其中RSU通信距离为500 m。MEC服务器、聚合服务器和云服务器的计算能力分别设置为F1=1×109Hz,F2=2×1010Hz,F3=1×1011Hz。发射功率为p1= 2 W,有线数据传输速率为Ras=2Rcs=10 Mbit/s,高斯噪声功率谱密度为N0=-174 dBm/Hz,信道增益为hi=127+30lgd。系统总带宽为20 MHz,每个子通道的带宽为1 MHz。
首先分析了不同折扣因子对收敛性的影响,如图3所示。将折扣因子分别设置为0.9、0.7和0.1。由图3可知,随着折扣因子的增大,训练损失收敛的速度越快。这是因为如果折扣因子设置过小,系统只能在短期内降低系统的总长期成本。若增大折扣因子,系统对未来奖励的重视越高,在长期奖励上就越有保证。
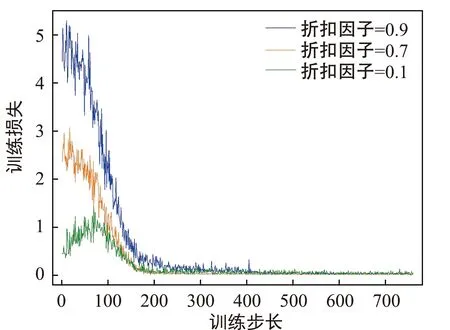
图3 折扣因子对收敛性的影响
图4分析了学习率对训练损失的影响,从图4可以看出,随着训练步数的增加,DQN算法可以有效地收敛。将学习率分别设置为0.01、0.001、0.000 1,可以得到,当学习率为0.001时,训练损失收敛速度最快。这是因为学习率决定了权重在梯度方向变化的步长。学习率越大,权重变化越大容易导致跳过全局最优值而陷入局部最优值;若学习率设置较小,则每一步的损失函数最小值的方向都比较小,会浪费更多的时间来优化。
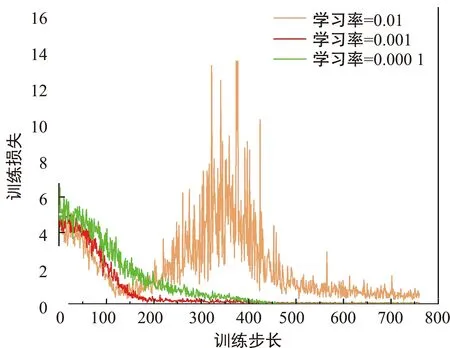
图4 学习率对收敛性的影响
为了验证CEC-DQN算法的性能,本文选择了MEC Offloading (MO)、Cloud Offloading (CO)和Random Offloading (RO)三种计算方法与CEC-DQN算法进行比较。图5显示了不同算法下任务数据大小对系统总成本的影响,其中每个任务的数据大小设置为2~10 MB不等。从图5可以看出,随着任务数据大小的增加,系统总成本也会增加。与CO、RO和MO算法相比,CEC-DQN算法的系统总成本平均分别降低了7%、13%和22%。这表明,CEC-DQN算法可以整合系统当前和未来的状态,可以更一致地优化系统总成本。
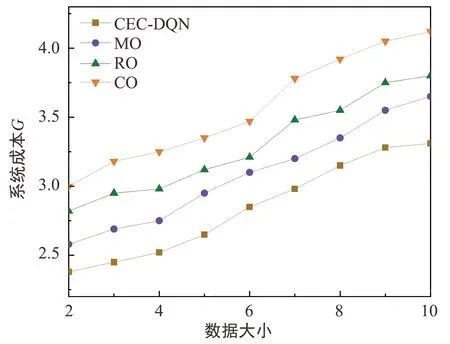
图5 任务数据量对成本G的影响
图6分析了不同算法下MEC服务器计算能力对系统总成本的影响,其中服务器的计算能力设置为2~8 GHz不等。在图6中,随着MEC服务器计算能力的增加,系统总成本呈下降趋势。与CO、RO和MO算法相比,CEC-DQN算法的系统总成本平均分别降低了5%、15%和23%。这表明,任务的计算量与边缘服务器的计算能力呈正相关,且CEC-DQN方法在VEC网络中的能耗、时延控制和可靠性方面优于基准策略。
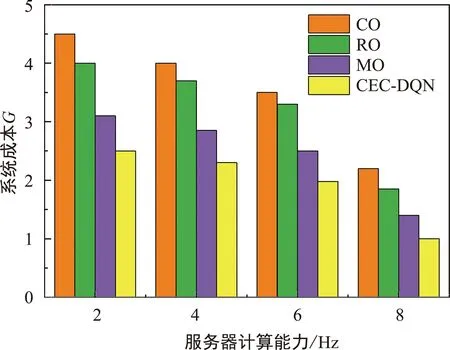
图6 MEC服务器计算能力对成本G的影响
6 结束语
面对车载边缘计算网络中高性能需求,为解决通感算融合网络中边缘节点缺失智能化处理现状,本文基于分布式计算与云边端一体化技术,提出一种高效的车载边缘计算卸载策略来最小化系统的长期总成本,实现VEC网络通感算资源调度优化。首先将算力与网络深度融合,协同分布式计算资源提出了一种适用于多用户的协同分层智能驱动VEC算力网络体系架构,利用云中心、聚合服务器和MEC服务器的异构计算能力,有效应对边缘节点在多层算力网络中实现算力均衡。在此基础上,联合优化卸载决策与资源配置机制,将其转化为MDP问题。最后,提出了一种基于CEC-DQN的算法来解决MDP问题,为提高通感算融合系统的网络容量、计算效率提供了支持。仿真结果表明,与CO、RO和MO算法相比,CEC-DQN算法在优化系统长期总成本方面的平均性能优势分别约为6%、14%和22.5%。在未来的研究中,将面向车载边缘计算中通感算融合系统中实时边缘智能难题进行更深入的探讨,为后续课题奠定研究基础。

