LSSVM算法下飞机IDG小样本数据可靠性分析

孔祥芬，刘敬赟，王 杰，唐淑珍

（中国民航大学航空工程学院，天津 300300）

1 引言

随着航空科学技术日益蓬勃发展，民用飞机的先进机载用电设备大幅增加，对飞机供电系统的要求和依赖性进一步提高[1]。整体驱动发电机（IDG）作为飞机供电系统的核心电源部件，为机载用电设备提供恒频交流电[2]，其可靠运行是飞机飞行安全的重要保障。近年来，我国正处于由民航大国向民航强国迈进的关键时期，民航“一二三三四”总体工作思路和“民航高质量发展”战略需求都对航空附部件产品的可靠性提出了更高的要求。从飞机IDG的历史故障数据出发，结合数据特点对其进行可靠性分析，了解IDG故障的变化规律，对提高飞机IDG的使用可靠性及制定经济合理的维修策略具有重要意义。

对于飞机IDG这样的航空附部件产品，其可靠性要求高且价格高昂数量少，从而可获得的故障数据较少属于小样本（n≤30）范畴。目前，在航空附部件产品的可靠性分析方面，国内外学者针对小样本故障数据的分析研究较少。如，文献[3]采用利用EM算法估计飞机IDG在故障数据删失情况下威布尔分布的未知参数；文献[4]运用Bootstrap方法对飞机IDG进行可靠度、平均故障间隔时间的点估计和区间估计计算；文献[5]通过对比分析中位秩法和平均秩次法两种经验分布函数，得到综合最小二乘法及平均秩次法所得到的某航空装备的可靠性参数估计精度更高；文献[6]运用极大似然值法求解了飞机无线电子设备在退化状态情况下的参数估计问题。然而，上述所运用的可靠性统计研究方法相较于飞机IDG的小样本故障数据特征难以获得较好的效果，会造成计算结果与实际情况之间存在误差。

支持向量机（Support Vector Machine，SVM）作为近年来基于统计学习理论发展起来的一种机器学习方法[7]，以结构风险最小化作为目标函数，无需先验知识。在解决小样本实际问题中表现出独特的优势[8]。文献[9]利用SVM模型训练样本进而对数据进行预测扩充，最后利用扩充后的样本进行可靠性参数估计；文献[10]结合实例，利用支持向量机回归法、蒙特卡罗法等模型方法，分别对连杆的变形和摇杆的摆角进行可靠性对比研究分析；文献[11]指出SVM回归模型具有训练速度慢、存储量大的难题。文献[12]提出一种支持向量机的改进算法—最小二乘支持向量机算法（Least Squares Support Vector Machine，LSSVM）对服从威布尔分布的发动机系统进行参数估计。并指出该方法在保证精度的同时改善了SVM回归模型训练速度慢的问题。

上述研究成果表明，LSSVM 算法可以得到小样本数据下较为理想的可靠性参数估计结果。

研究和实践结果表明，飞机机电、液压等系统以及其子系统、零部件大都适用威布尔分布来拟合[4，13−14]。因此，在现有的研究基础上，以威布尔分布为例，将LSSVM算法应用到小样本故障数据下飞机IDG可靠性分析中。

采集到某航空公司3年45架B737−800飞机IDG部件的历史故障数据作为LSSVM模型的训练样本，采用网格搜索法和交叉验证法寻找LSSVM模型中的最优参数，继而结合图估计法对可靠性分布参数进行估计，并与最小二乘法的参数估计结果进行对比研究。

2 LSSVM算法介绍

2.1 LSSVM回归模型

文献[15]于1999 年在SVM 的基础上提出了LSSVM。与SVM相比，LSSVM在优化问题中使用的是平方误差项而非ε−不敏感损失函数，即LSSVM利用求解一组等式约束替代了SVM在对偶空间中求解二次规划的问题。

从而降低了模型优化过程中的复杂性，克服了模型训练时间较长的问题，且提高了收敛精度。

对于给定的数据集：

LSSVM回归模型可表示为求解以下优化问题：

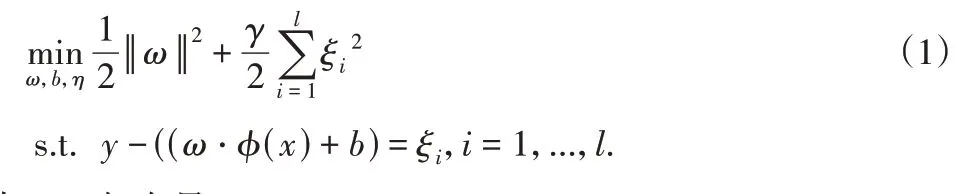
式中：ω—权向量；

ϕ(x)—非线性函数，将非线性函数映射到高维特征空间构造线性回归；

b—偏置项；

γ—正则化常数；

ξi—误差项。

一般用拉格朗日法求解这类优化问题：

引入核函数K(xi，xj)=ϕ(xi)⋅ϕ(xj)，K(xi，xj)是满足Mercer条件的核函数。根据式（3），优化问题转化为求解线性方程：

2.2 LSSVM参数选择

LSSVM 模型性能的好坏取决于核函数及其参数、正则化参数γ的影响。其中核函数K(xi,xj)主要有线性（Linear）核函数，径向基（Radial Basis Function，RBF）核函数，多项式（Polynomial）核函数等，这里运用一般工程实际问题通常采用的径向基核函数。

经过以上分析可知采用RBF核函数的最小二乘支持向量机模型中包含两个参数，即正则化参数γ和RBF核参数σ2，二者的取值对模型的学习能力和泛化能力有很大的影响。LSSVM回归模型参数的选择是一个寻优过程，通常采用的方法有网格搜索法、梯度下降法、数值估计法等。

鉴于采集的数据集为小样本，这里采用网格搜索法和交叉验证法对参数组合(γ，σ2)进行寻优。该方法可同时对σ2和γ进行穷举搜索。令：

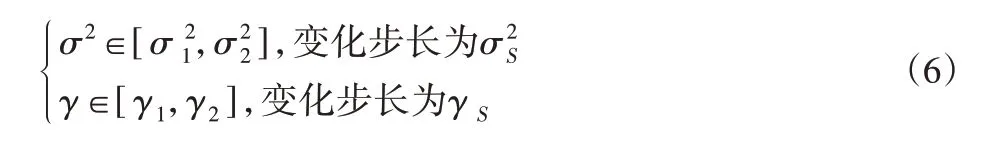
根据所设定的范围和步长将σ2和γ可能的取值进行组合(γ，σ2)，在模型尝试了所有的参数组合列出所有可能的组合结果生成“网格”，利用交叉验证法求得样本点与回归拟合点间的均方误差，取其中误差最小的一组参数组合作为模型参数[9]，同时可得所求最优回归直线。

3 LSSVM算法下的威布尔分布参数估计

3.1 威布尔分布及其线性化

威布尔分布模型能够描述失效率浴盆曲线各个阶段的分布规律，比其他分布模型的适用范围更广[16]。是机械、电子等领域广泛使用的连续型分布。两参数威布尔分布的累计失效概率函数为：

式中：t—部件产品的故障时间；β—形状参数；η—尺寸参数。

一般地，当样本量n≤20时通常采用中位秩公式来计算累计失效概率密度：

式中：n—样本量；i—样本故障时间从小到大排序序号。

进一步将威布尔分布模型线性化，可得：

对于一组故障数据样本{ }ti，i=1，....n，将数据线性化后得到数据集T={(x1，y1)，(x2，y2)，…(xn，yn)}。

数据集T={(x1，y1)，(x2，y2)，…(xn，yn)}线性相关程度通常用相关系数ρxy来表示：

3.2 基于LSSVM回归模型的参数估计

若样本数据可较好的服从两参数威布尔分布，则进一步运用LSSVM回归模型对线性化后的数据集:

进行回归拟合，得到最优回归直线。

根据式（10）和式（11）可知，所得到的最优回归直线的斜率即为形状参数β的值。另外，尺寸参数η又称特征寿命，为累计故障失效率F(t)=63.2%时所对应的寿命。根据式（10）可知，当累计故障失效率F(t)=63.2%时对应的yi=0，从而直线yi=0与最优回归直线交点的横坐标即为lnη的值。

3.3 回归拟合结果的评价

通常，可采用统计学中的以下指标对不同回归拟合方法所得结果进行定量评估。

（1）决定系数，即R2(R−Square)。

均方根误差（RMSE）为：

均方根误差越接近0，表明拟合效果最好。

4 案例分析

4.1 飞机IDG部件介绍

飞机整体驱动发电机（IDG）又称组合驱动发电机，是目前国内外民航运输业中大型客机如B707、B737、B747、A320等供电系统的主要电源。以B737−800飞机为例，每架B737−800飞机配备有两台IDG，分别位于左、右发动机附件轮箱的前面。

飞机IDG主要由液压机械恒速传动（CSD）装置，空气/滑油冷却器和无刷交流发机三部分组成，工作原理为：发动机附件齿轮箱传递变化的转速带动IDG主轴转动，通过液压恒速传动装置将变速转化为恒速，驱动其内部交流发电机转子转动，进而为飞机机载用电设备提供恒频交流电。

其可靠性框图，如图1 所示。作为飞机供电系统的核心部件，飞机IDG的可靠性水平直接影响了飞机系统的安全性和可靠性，因此进一步统计飞机IDG的故障数据，对飞机IDG进行可靠性分析。

图1 飞机IDG可靠性框图Fig.1 Reliability Block Diagram of Aircraft IDG

4.2 数据采集与预处理

以国内某航空公司45架B737−800飞机机组为研究对象，采集到该机组2015年2月到2018年7月供电系统的现场故障数据电子记录。

其中所考虑的飞机IDG故障主要包括两种类型：

（1）在故障描述中表明飞机IDG中的某零部件异常，如过站检查发现右发IDG空气滑油冷却器漏滑油，并在排故措施中采取更换该零部件的措施；

（2）在故障描述中体现与飞机IDG相关的异常现象，如地面滑行时右发SOURCE OFF 灯亮等，因此在排故措施中采取更换IDG等措施。

经过对该机组供电系统故障记录的筛选、归类处理，得到飞机IDG的故障数据即单机同一IDG部件相邻两次故障间的飞行时间（即可靠性指标故障间隔时间），共计15条，部分故障数据记录，如表1所示。

表1 飞机IDG的部分故障数据记录Tab.1 Partial Fault Data Record of Aircraft IDG

将15条飞机IDG故障数据按照从小到大升序排列，具体统计结果表2第二列所示。

根据式（3）对该数据样本进一步线性化处理得到数据集T=(x1,y1),(x2,y2),...,(xn,yn)，如表2中的第3、4列所示。

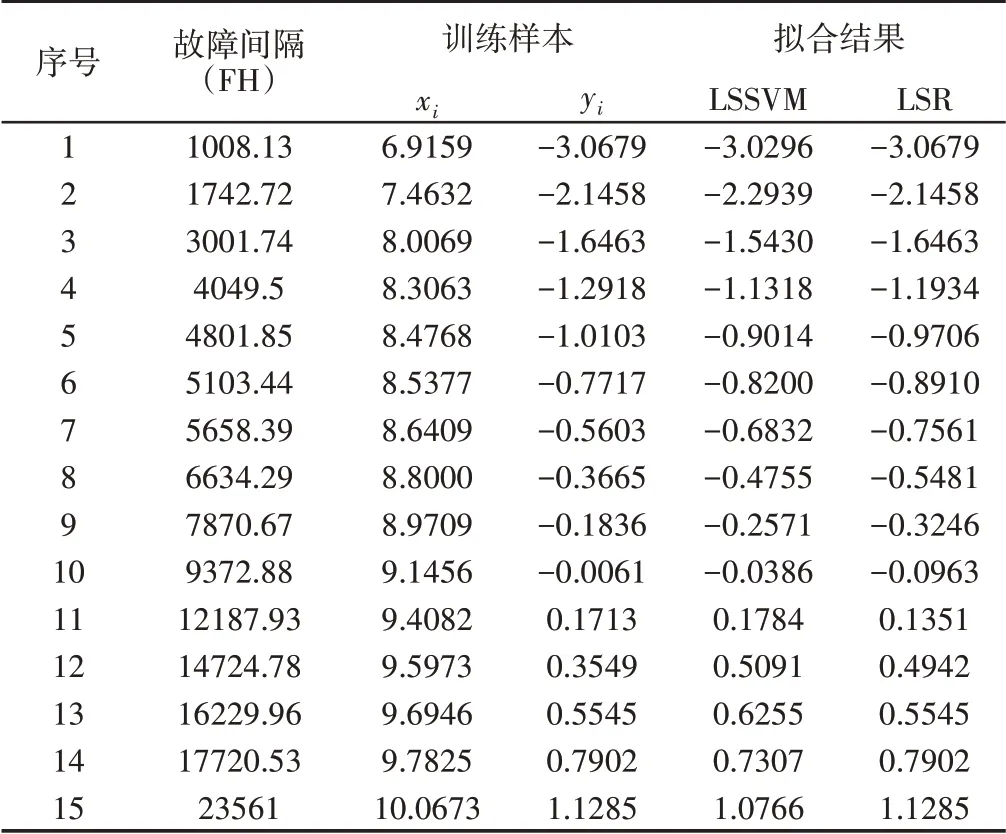
表2 故障数据、训练样本数据及拟合结果Tab.2 Fault Data，Training Sample Data and Fitting Results

经计算，x与y之间的相关系数ρxy为：

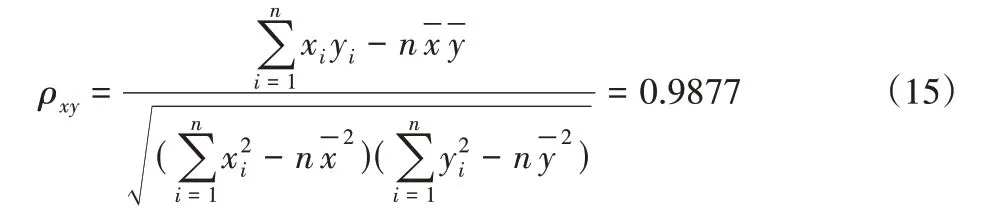
由计算结果可知，二者近似线性关系，说明B737−800 飞机IDG故障的寿命分布较好的服从二参数威布尔分布。

4.3 可靠性参数估计结果

将线性化处理得到数据集T=(x1，y1)，(x2，y2)，...，(xn，yn)，作为LSSVM回归的训练样本。首先，采用网格搜索法和交叉验证法对LSSVM模型进行参数寻优，其中搜索范围和步长如下：

通过寻优计算，得到最优参数组合γ=100005，σ2=12。拟合结果，如表2 第5 列所示。同时得到最优回归直线，如图2 所示。其中，该直线的斜率即形状参数β=1.2409。通过图2中虚线所示，直线y=0与回归直线的交点A对应的横坐标的值即x=lnη，从而得到尺寸参数η=9823.6694。

图2 LSSVM算法下的最优回归拟合直线Fig.2 Optimal Regression Fitting Line in LSSVM Algorithm

4.4 可靠性参数估计结果对比评价

为验证LSSVM算法的有效性和准确性，采用可靠性分析中传统的最小二乘法（Least Squares Regression，LSR）进行对比。其中采用最小二乘法进行回归拟合，拟合结果如表2第5列所示，参数估计结果，如表3所示。分别运用式（13）和式（14）指标对两种方法进行误差分析，结果，如表3所示。

根据表3 中结果可知，使用两种方法所得参数结果基本一致，其中LSSVM算法下的决定系数R2偏大，均方根误差RMSE偏小。可说明运用LSSVM算法可以得到小样本下飞机IDG的可靠性参数估计结果，且估计精度得到了提高。该结果与文献[17]的结果相同。

表3 可靠性参数估计结果及误差分析Tab.3 Reliability Parameter Estimation Results and Error Analysis

5 飞机IDG部件的可靠性分析

B737−800飞机IDG的故障寿命分布较好的服从两参数威布尔分布，由所识别的形状参数和尺度参数，得到该B737−800机组的飞机IDG部件失效率、可靠度曲线，如图3、图4所示。

图3 飞机IDG的失效率曲线Fig.3 Failure Rate Curve of Aircraft IDG

图4 飞机IDG的可靠度曲线Fig.4 Reliability Curve of Aircraft IDG

从失效率、可靠度曲线趋势来看，使用两种算法得到的趋势相同，但存在一定的偏差。

其中LSSVM算法下得到的飞机IDG部件失效率偏高，可靠度偏低。

LSSVM 算法下计算得到形状参数β=1.2409，β>1，说明飞机IDG的失效率随时间的增长而增加，故障类型为耗损故障。

一般当β>1 时，表明该部件失效往往会集中在某一时刻后不太长的时间段内，对这类部件一般采用预防性维修最为有效，在规定期限内进行状态检测以减少不必要的维修，节约维修成本。

通常采用的状态检测周期为Tm=0.1MTBF，其中两参数威布尔分布的平均故障间隔时间为：

代入尺寸参数η=9823.6694，形状参数β=1.2409，得到Tm=916.5484。因此建议每隔917Fh对该B737−800飞机机组的IDG部件进行状态检修。

6 结论

针对飞机IDG作为航空高可靠性产品故障数据为小样本的特点，这里提出将小样本数据分析方法引入飞机IDG部件的可靠性分析中。可得到以下结论：

（1）通过对比LSSVM算法和最小二乘法的可靠性分析效果，得到基于LSSVM算法下飞机IDG的可靠性分析精度较高。两种方法下得到的可靠度曲线趋势一致，LSSVM 算法下的可靠度较低，可更加客观的评价飞机IDG的可靠性。

（2）经计算得到，该B737−800机组飞机IDG部件故障时间服从形状参数为β=1.2409，尺度参数为η=9823.6694的两参数威布尔分布。在对飞机IDG进行预防性维修方面，建议每隔917Fh对飞机IDG部件进行状态检修。

（3）此外，该小样本情况下的可靠性分析方法还可以为飞机其他高可靠性系统、子部件以及其他领域装备的可靠性分析提供参考依据。